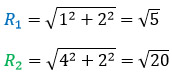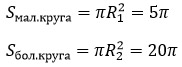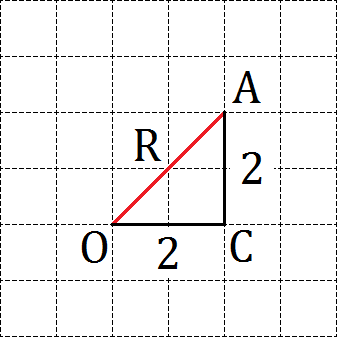Решение:
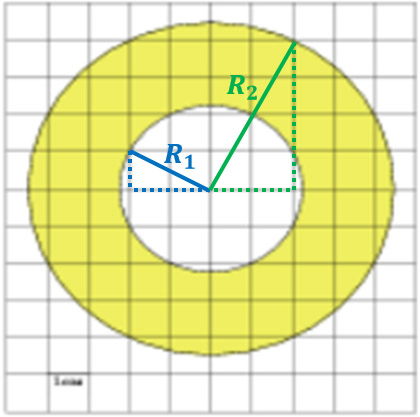
Окружности нарисованы не очень удачно потому, что мы не можем с точностью сказать, какова длина у их радиусов. Придется искать.
Начертим радиусы этих двух окружностей так, как показано на рисунке, а затем сделаем еще одно дополнительное построение: достроим эти радиусы до прямоугольных треугольников.
Теперь с помощью теоремы Пифагора можно найти длины радиусов.
Далее найдем площадь маленького круга с радиусом R1 и большого круга с радиусом R2.
Чтобы найти площадь кольца надо из площади большого круга вычесть площадь маленького:
В ответе нас просят записать площадь, деленную на π, т.е. просто 15.
Ответ: 15.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#799
3 октября 2013
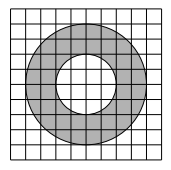
Сегодня мы разберем нестандартную задачу B5 на площади из ЕГЭ по математике. В этой задаче требуется найти площадь закрашенного кольца, которое представляет собой две концентрические окружности разных радиусов:
Задача. Найдите площадь S закрашенного кольца, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как и во всех задачах, для решения нам потребуется формула площади круга:
S = πR2
где R — радиус круга. Это стандартная формула, и ее обязательно надо знать. Но поскольку в задаче фигурируют два круга, то и радиусов будет два. Обозначим внутренний радиус (меньшей окружности) буквой R1, а внешний радиус — R2. Внутренний радиус очень легко считается, он равен двум клеточкам:
R1 = 2 ⇒ R12 = 4
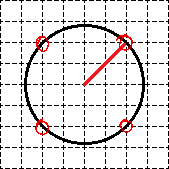
Со вторым радиусом все сложнее. Окружность не проходит через «классические» точки горизонтальной и вертикальной осей, по которым обычно измеряется радиус. Однако на этой окружности есть другие точки, которые лежат в узлах исходной сетки. Отметим эти точки красным:
Что дают нам эти точки? Как минимум — визуальное представление того, как выглядит радиус. Для того, чтобы его вычислить, давайте отдельную сетку, на которой отметим центр окружности O и ту точку A на нашей окружности, в которую мы провели радиус. Затем достроим полученный отрезок до прямоугольного треугольника, двигаясь вдоль линий сетки. Получим треугольник OAC с прямым углом C:
По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) получаем:
R2 = OA2 = OC2 + AC2 = 22 + 22 = 4 + 4 = 8
Итого мы получили:
R22 = 8
Теперь осталось найти площади внешнего и внутреннего кругов, образующих кольцо:
S1 = πR12 = π · 4 = 4π;
S2 = πR22 = π · 8 = 8π.
Поскольку закрашенное кольцо лежит между границами кругов, для нахождения его площади надо из площади большего круга S2 вычесть площадь меньшего круга S1. Получаем:
S = S2 − S1 = 8π − 4π = 4π
Но это еще не ответ! В задаче требуется найти величину S/π. Давайте сосчитаем:
S/π = 4π/π = 4
Вот мы и получили ответ! Как видите, ничего сверхъестественного в этой задаче нет. Достаточно помнить формулу площади круга, а также находить эту площадь через радиус, даже если этот радиус приходится считать через теорему Пифагора.
Надеюсь, этот урок сильно поможет тем, кто всерьез готовится к ЕГЭ по математике. Тем, кто не рассчитывает на то, что им попадутся легкие задачи (в частности, задача B5), а готовится решать в том числе и нестандартные примеры. В общем тренируйтесь — и обязательно сдадите экзамен на отличный балл.:)
Смотрите также:
- Нестандартная задача B5 на площадь круга
- Задача B5: площадь закрашенного сектора
- Десятичные дроби
- Специфика работы с логарифмами в задаче B15
- Семинар: ЕГЭ по математике, задачи B3 на площади
- Решение задач на движение по воде
Всем известно, что площадь круга высчитывают по формуле S=πR²
То есть всегда необходимо знать радиус, чтобы найти площадь.
Судя по условию задания и по рисунку,
радиус большого круга — 2 см, а радиус внутреннего — 1 см, а постоянное число π = 3,14.
Высчитываем площадь большого круга
S = 3,14 х 2 х 2 = 12,56.
Площадь внутреннего круга
S = 3,14 х 1 х 1 = 3, 14.
Площадь кольца можно найти вычитанием и площади большого круга площадь внутреннего.
12,56 — 3,14 = 9,42.
Если выяснять, сколько это частей π, непонятно только, зачем?
9,42 : 3, 14 = 3.
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
26 мая
Как заработать +20−30 баллов на ЕГЭ благодаря разборам ЕГЭ с ДВ? Присоединиться
24 мая
Обновлённая панель инструментов
22 мая
Беседы Решу ЕГЭ по подготовке к ЕГЭ
11 мая
Решение досрочных ЕГЭ по всем предметам
5 мая
Обновленный поиск заданий по ключевым словам
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Поиск
?
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Всего: 2 1–2
Добавить в вариант
Тип 12 № 245008
i
Найдите (в см2) площадь S кольца, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). В ответе запишите
Аналоги к заданию № 245008: 263479 263419 263421 … Все
Решение
·
Помощь
Тип 12 № 263479
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). В ответе запишите
Аналоги к заданию № 245008: 263479 263419 263421 … Все
Решение
·
Прототип задания
·
Помощь
Всего: 2 1–2
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Найдите площадь кольца, изображённого на рисунке…
Условие задачи:
Найдите площадь кольца, изображённого на рисунке, если площадь круга, ограниченного большей окружностью, равна 132.
Решение:
Ответ: 99
- 1
- 2
- 3
- 4
- 5
Оценка: 5.0 из 1
Комментарии
Всего комментариев
: 0