Инфоурок
›
Математика
›Презентации›Вычисление на клетчатой бумаге. Площадь. 9 класс подготовка к огэ
Скачать материал

Скачать материал






- Сейчас обучается 41 человек из 29 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Подготовка к огэ 9 класс
Вычисление площади многоугольника
на клетчатой бумаге.
Выполнила учитель математики Полякова Светлана Владимировна МБОУ «Благовещенская ООШ» -
-
3 слайд
Вычисление площади многоугольника
на клетчатой бумаге.
Е ГЭ -
4 слайд
Цель: найти способы нахождения площадей многоугольников, научиться выбирать рациональный способ решения задачи в конкретных случаях
Задачи:
изучение и анализ информации по указанной теме;
поиск способов нахождения площадей многоугольников на клетчатой бумаге ;
решение заданий из открытого банка заданий ОГЭ — показ практического применения результатов исследования. -
5 слайд
Одним из основных заданий Модуля Геометрия являются задачи на нахождение площади фигур на сетке. Многие ученики сводят решение этого задания к подсчету клеток внутри фигуры. Такой способ не всегда дает точный результат. Поэтому я предлагаю рассмотреть основные способы решения таких задач.
-
6 слайд
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
-
7 слайд
Основные свойства площадей
Площадь многоугольника— положительное число
Равные многоугольники имеют равные площади.2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
3. Площадь квадрата равна квадрату его стороны
S = S₁ + S₂+ S₃
a
a
S = a²
S₁
S₂
S₃F₁
F₂ -
8 слайд
Формулы вычисления площадей многоугольников
-
9 слайд
Формулы вычисления площадей многоугольников
-
10 слайд
Способы вычисления площадей фигур на клетчатой бумаге
-
11 слайд
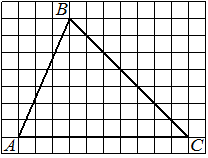
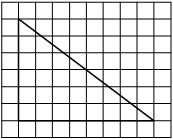
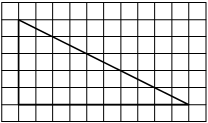
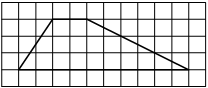
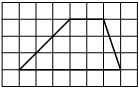
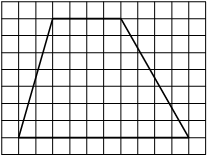
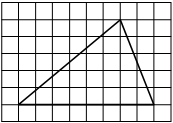
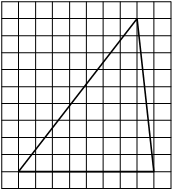
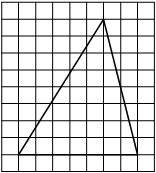
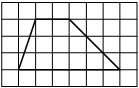
Задача.
На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рис.).
Найдите его площадь в квадратных сантиметрах. -
12 слайд
7
3
1
2
4
5
6
8
9
10
« Считаем по клеткам»
1.Посчитаем количество полных клеток внутри данного треугольника.
10
2.Дополним неполные клетки до полных клеток.
5
3. Сложим полученные количества полных клеток:
10+5=15
Ответ: 15
1
2
3
4
это ½ клетки
это ½ клетки
5
Способ 1 -
13 слайд
а
h
Площадь искомого треугольника найдем по формуле:
Sтр=(а•h)/2,
где а – основание треугольника,
h – высота, проведенная к этому основанию.
а= 6 , h=5
Получаем
Sтр=1/2*6*5= 15Способ 2
Использование формул планиметрии -
14 слайд
1.Разобьем данный треугольник на два прямоугольных треугольника, для этого проведем высоту.
2.Найдем площадь прямоугольного треугольника S1 =1/2*5*5=12,53.Найдем площадь прямоугольного треугольника S2=1/2*1*5= 2,5
4.Площадь искомого треугольника найдем по формуле:
Sтр=S1+S2= 15
5
1
5
S1
S2
Способ 3
Разбиение многоугольника на части. -
15 слайд
5
6
5
5
1
S1
S2
1.Достроим до прямоугольника со сторонами 5 и 6.2.Найдем площадь прямоугольника:
Sпр = 5*6=30
3.Найдем площадь прямоугольного треугольника S1=1/2*5*5=12,5
4.Найдем площадь прямоугольного треугольника S2=1/2*1*5=2,5
5.Площадь искомого треугольника найдем по формуле:
S=Sпр-(S1+S2)
S =30- 15=15
Способ 4
Достраивание до прямоугольника
S -
16 слайд
Георг Алекса́ндр Пик
(10.08.1859-13.07.1942) ,
австрийский математик.
Широкую известность получила открытая
им в 1899 году теорема Пика для расчёта
площади многоугольника.
Площадь многоугольника
с целочисленными вершинами равна
S = В + Г: 2 — 1
где В — количество целочисленных точек внутри многоугольника,
Г — количество целочисленных точек на границе многоугольника.
Точка координатной плоскости называется целочисленной, если обе её координаты целые. -
17 слайд
В=4
Г=12S = 4 + 12 : 2 – 1 = 9
Способ 5 Применение формулы Пика
Площадь многоугольник можно
найти по следующей формуле: S = В + Г: 2 — 1S = В + Г : 2 — 1
-
18 слайд
Применение формулы Пика
S= В+ Г:2-1 -
19 слайд
Формула Пика. Площадь многоугольника с целочисленными вершинами равна
S= В+ Г:2-1Г – количество точек на границе фигуры
В – количество точек пересечения решётки внутри фигуры.
S=13+6:2-1=15
S=7+8:2-1=10 -
20 слайд
Способы вычисления площадей фигур на клетчатой бумаге
« Считаем по клеткам»
Использование формул планиметрии
Разбиение многоугольника на части.
Достраивание до прямоугольника
Применение формулы
Пика -
21 слайд
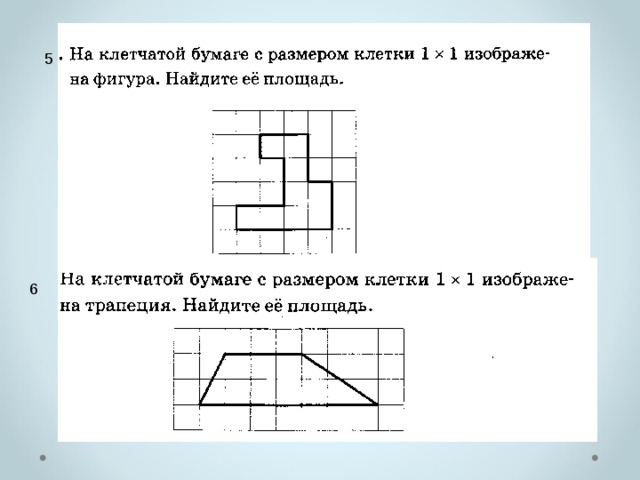
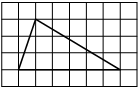
1.Как вычислить площадь данного многоугольника ?
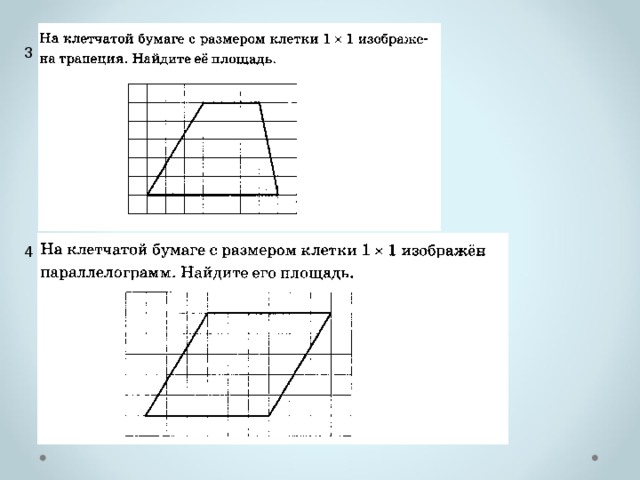
Размер клетки 1см х 1см. -
22 слайд
2.Как вычислить площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
1 см x 1 см?
. -
23 слайд
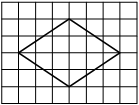
3.Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
1 см x 1 см -
24 слайд
Способ 2
Использование формул планиметрии
S =3*5=15
S =1/2*6*2=6 -
25 слайд
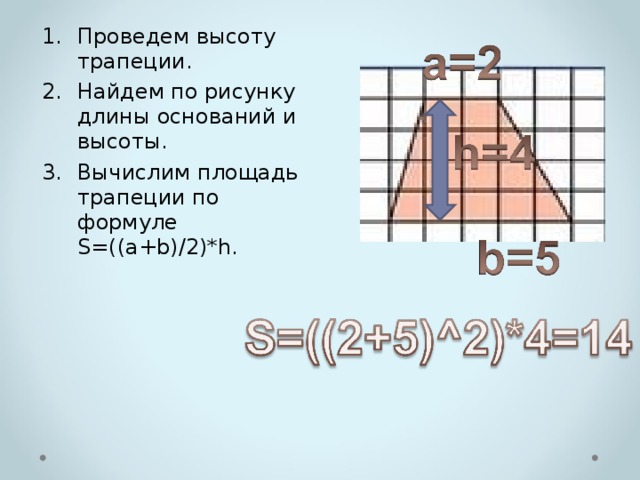
Проведем высоту трапеции.
Найдем по рисунку длины оснований и высоты.
Вычислим площадь трапеции по формуле S=((a+b)/2)*h.
S=((2+5)^2)*4=14
а=2
h=4
b=5 -
26 слайд
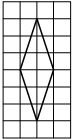
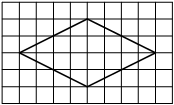
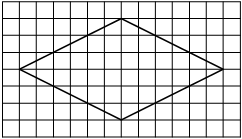
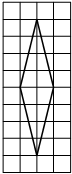
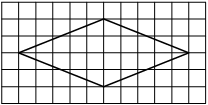
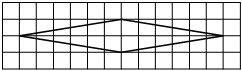
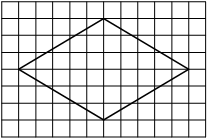
Проведем диагонали ромба.
Найдем их длины по рисунку.
Найдем площадь ромба по формуле S=1/2*d1*d2.
d2=6d1=4
S=1/2*4*6=12 -
27 слайд
Способ 3
Разбиение многоугольника на части
S1
S2
S =6+6=12
S =1,5*4+4=10
S =5+10+10=25 -
28 слайд
Способ 4
Достраивание до прямоугольника
S =6*4-6*2=12
S=4*4-6=10 -
29 слайд
Способы вычисления площадей фигур на клетчатой бумаге
« Считаем по клеткам»
Использование формул планиметрии
Разбиение многоугольника на части.
Достраивание до прямоугольника
Применение формулы
Пика
S=(а•h)/2,
S = В + Г: 2 — 1
а
h -
30 слайд
Урок полезен, все понятно.
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 267 935 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 29.05.2018
- 429
- 2
Рейтинг:
4 из 5
- 29.05.2018
- 9161
- 245

Рейтинг:
5 из 5
- 29.05.2018
- 6914
- 233


- 29.05.2018
- 477
- 1



Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Скачать материал
-
29.05.2018
6301
-
PPTX
1.1 мбайт -
60
скачиваний -
Рейтинг:
4 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Полякова Светлана Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 3 месяца
- Подписчики: 4
- Всего просмотров: 37603
-
Всего материалов:
28
Решение задач на нахождение площади геометрических фигур на сетке.
ОГЭ . Задание № 19
Подготовила учитель математики МОУ Школа с.Харсаим Филиппова Р.Р.
Характеристика задания
Задание 19 ОГЭ по математике представляет собой задачу по планиметрии на вычисление по готовому чертежу, изображённому на клетчатой бумаге. В таких задачах данные представлены в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. Это задачи на вычисление углов, расстояний, площадей, связанные со всеми изучаемыми в школьном курсе фигурами. Клетки в таких задачах по сути выполняют роль линейки: посчитав «по клеточкам» необходимые длины и используя известные геометрические факты и свойства, можно довольно быстро получить ответ на вопрос задачи.
Определение
- Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник
Единицы измерения площади
За единицу измерения площадей принимают квадрат со стороной 1см.
- Квадратный метр , производная единица Международной системы единиц (СИ) ; 1 м² = 1 са ( сантиар );
- Квадратный километр , 1 км² = 1 000 000 м²;
- Гектар, 1 га = 10 000 м²;
- Ар (сотка), 1 а = 100 м²:
- Квадратный дециметр, 100 дм² = 1 м²;
- Квадратный сантиметр, 10 000 см² = 1 м²;
- Квадратный миллиметр, 1 000 000 мм² = 1 м²;
Свойства площади
- Фигуры имеющие равные площади называются равновеликими.
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата равна квадрату его стороны.
Основные формулы для нахождения площади.
Площади треугольников
S = ½*a*h S = ½*a*b sinα S = r*p
S =
S = — формула Герона
(p = — полупериметр)
S = π*R 2 площадь круга
Основные формулы для нахождения площади.
Площади четырехугольников
Прямоугольник
S=a*b S= ½* d 2 sinφ
а и в – стороны прямоугольника
d — диагональ прямоугольника
φ- угол между диагоналями
Квадрат
S = a 2 S =1/2* d 2
а – сторона квадрата
d — диагональ квадрата
Параллелограмм
S=a*h S=a*b*sinα
S= ½* d 1 *d 2 sinφ
Ромб
S=a*h S=a 2 sinα
S= ½* d 1 *d 2
Трапеция
S = S = ½* d 1 * d 2 sinφ
а и в – основания трапеции; -длина средней линии ; d 1 и d 2 -диагонали трапеции; sinφ -угол между диагоналями
Одним из основных заданий Модуля Геометрия являются задачи на нахождение площади фигур на сетке. Многие ученики сводят решение этого задания к подсчету клеток внутри фигуры. Такой способ не всегда дает точный результат. Поэтому я предлагаю рассмотреть основные способы решения таких задач.
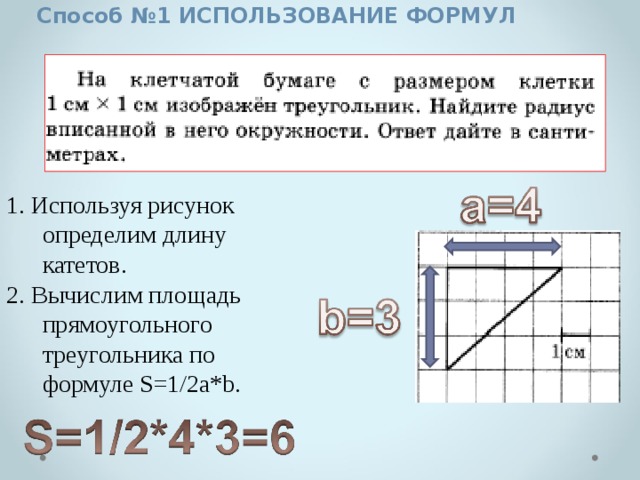
Способ №1 ИСПОЛЬЗОВАНИЕ ФОРМУЛ
1. Используя рисунок определим длину катетов.
2. Вычислим площадь прямоугольного треугольника по формуле S=1/2a*b.
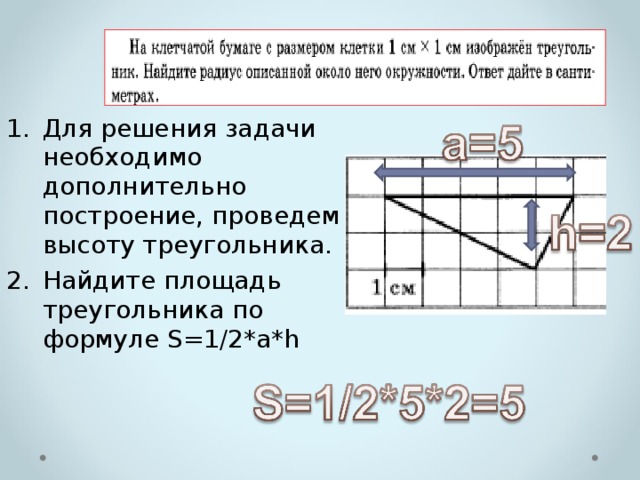
- Для решения задачи необходимо дополнительно построение, проведем высоту треугольника.
- Найдите площадь треугольника по формуле S=1/2*а*h
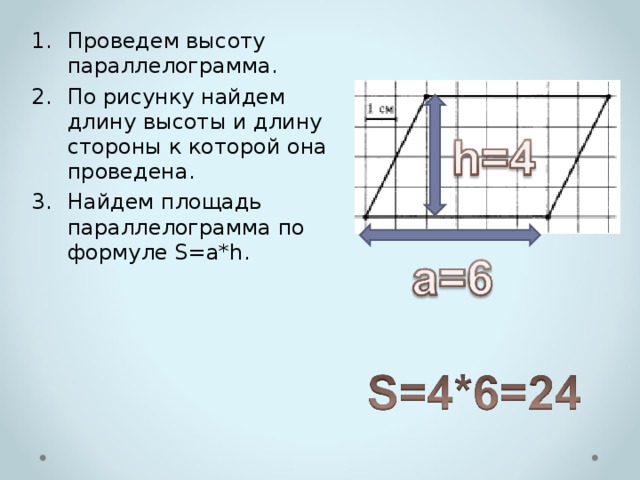
- Проведем высоту параллелограмма.
- По рисунку найдем длину высоты и длину стороны к которой она проведена.
- Найдем площадь параллелограмма по формуле S=a*h.
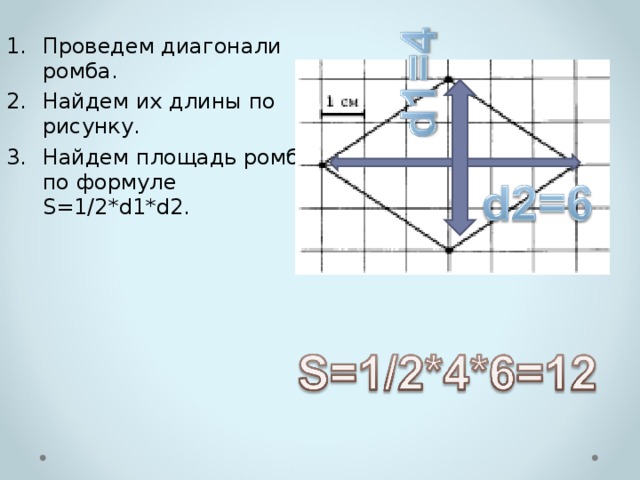
- Проведем диагонали ромба.
- Найдем их длины по рисунку.
- Найдем площадь ромба по формуле S=1/2*d1*d2.
- Проведем высоту трапеции.
- Найдем по рисунку длины оснований и высоты.
- Вычислим площадь трапеции по формуле S=((a+b)/2)*h.
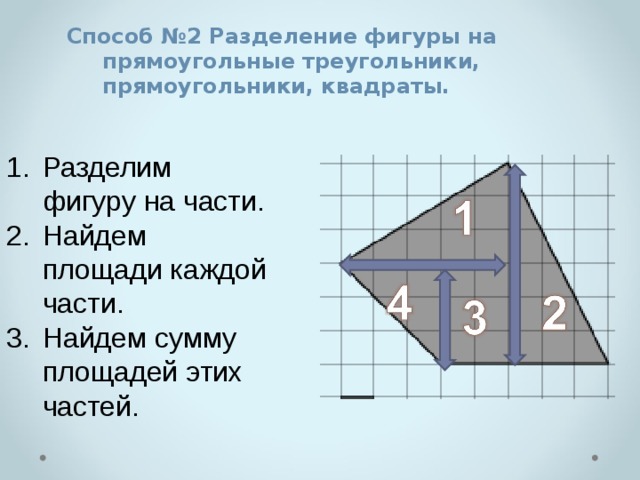
Способ №2 Разделение фигуры на прямоугольные треугольники, прямоугольники, квадраты.
- Разделим фигуру на части.
- Найдем площади каждой части.
- Найдем сумму площадей этих частей.
- Фигуры 1,4,2 –прямоугольные треугольники. Их площади найдем по формуле S=1/2*a*b.
- Фигура 3-прямоугольник. Его площадь легко найти даже подсчетам клеток. Его площадь равна 6.
- Сложив площади треугольников и прямоугольника мы найдем площадь искомой фигуры.
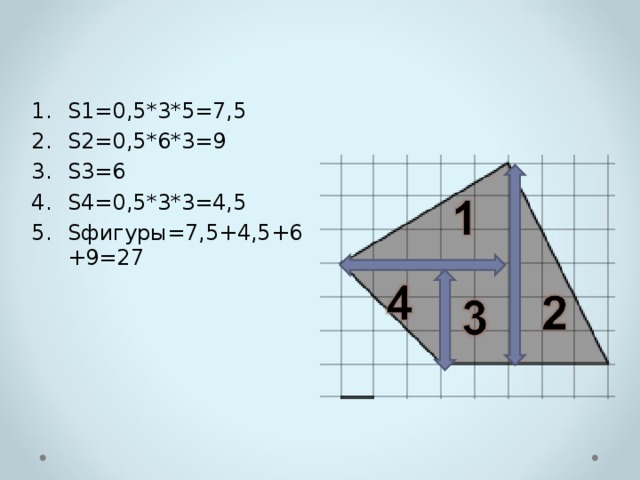
- S1=0,5*3*5=7,5
- S2=0,5*6*3=9
- S3=6
- S4=0,5*3*3=4,5
- Sфигуры=7,5+4,5+6+9=27
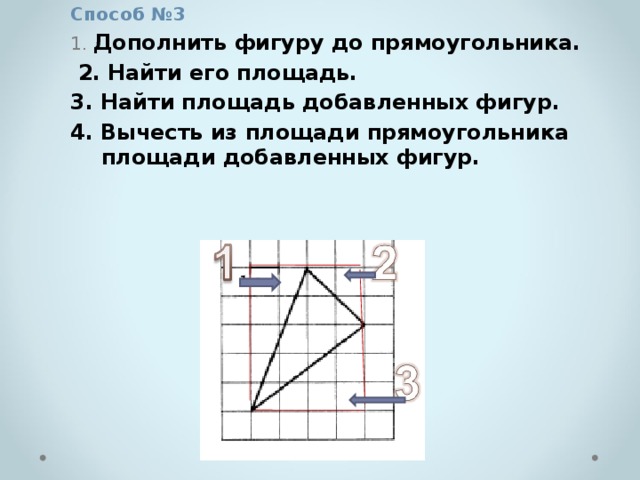
Способ №3
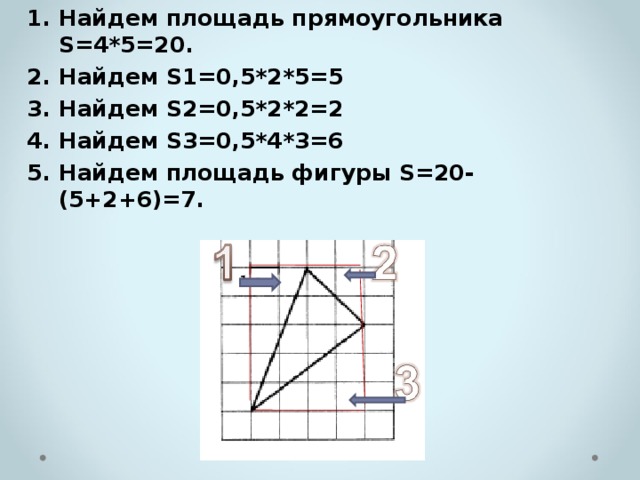
1. Дополнить фигуру до прямоугольника.
2. Найти его площадь.
3. Найти площадь добавленных фигур.
4. Вычесть из площади прямоугольника площади добавленных фигур.
- Найдем площадь прямоугольника S=4*5=20.
- Найдем S1=0,5*2*5=5
- Найдем S2=0,5*2*2=2
- Найдем S3=0,5*4*3=6
- Найдем площадь фигуры S=20-(5+2+6)=7.
Способ №4 Формула Пика.
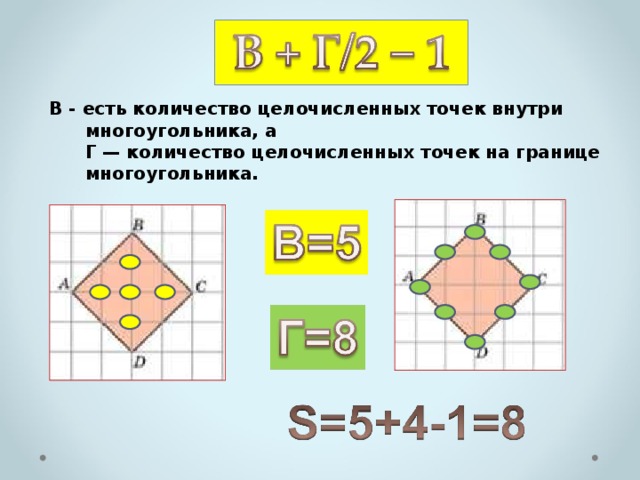
Площадь многоугольника с целочисленными вершинами равна В + Г/2 − 1 , где В — есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
В — есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
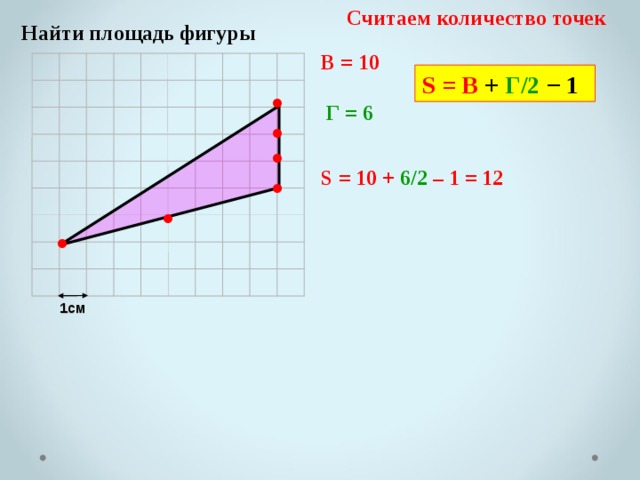
Считаем количество точек
Найти площадь фигуры
В = 10
S = В + Г/2 − 1
●
Г = 6
●
●
S = 10 + 6/2 – 1 = 12
●
●
●
1см
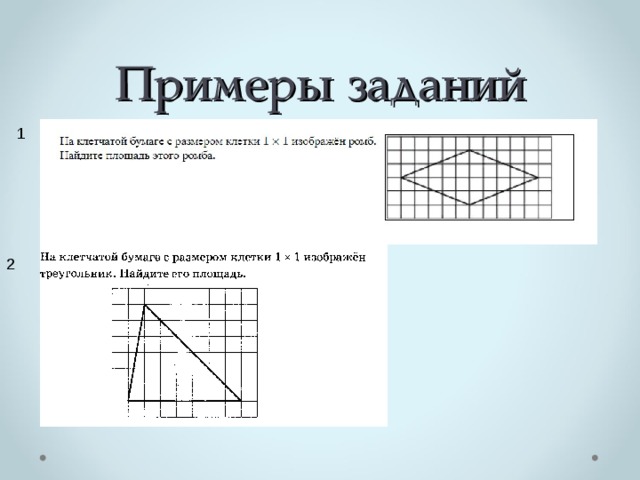
Примеры заданий
1
2
3
4
5
6
Определим, где находится комната Вики.
Из условия известно, что комната Вики находится на втором этаже рядом с комнатой Кости.
Комната Кости находится над кухней. Кухня обозначена цифрой 1. Это можно проверить. Длина кухни 6 клеток в 2 раза больше ширины в 3 клетки.
Комната Кости обозначена цифрой 7. Напротив находится комната Виктории. Она обозначена цифрой 6.
Из условия известно, что сторона клетки равна 1 м. Поэтому достаточно посчитать количество клеток в комнате.
Если масштаб не равен 1, необходимо разбить площадь комнаты на площади простых фигур. Посчитать их площадь и просуммировать.
3*1+5*3=18 м2.
Это задание из ОГЭ по математике предлагает найти площади, углы, длины геометрических фигур, нарисованных на фоне в клетку. Задание 18 с кратким ответом, в ответ идет только число.
Реальные задания №18 по геометрии из банка ФИПИ
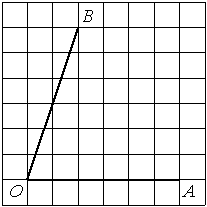
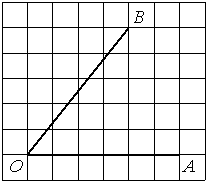
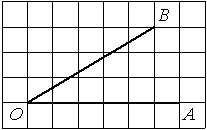
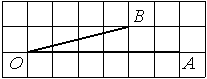
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=6/2=3.
Ответ: 3
AE8B22
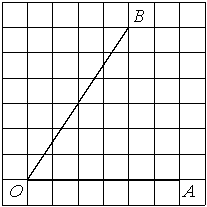
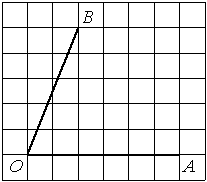
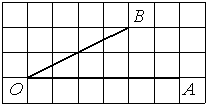
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=6/4=1,5.
Ответ: 1,5
09C3B1
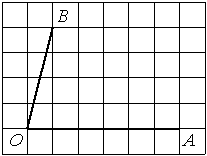
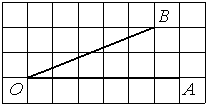
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=5/4=1,25.
Ответ: 1,25
739060
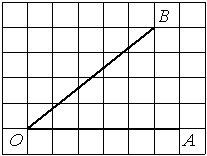
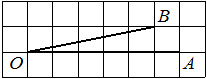
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=5/2=2,5.
Ответ: 2,5
0747AA
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4/1=4.
Ответ: 4
9C09A9
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4/5=0,8.
Ответ: 0,8
A1ECAA
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=3/5=0,6.
Ответ: 0,6
887E42
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=2/4=0,5.
Ответ: 0,5
201054
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=2/5=0,4.
Ответ: 0,4
E73651
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=1/5=0,2.
Ответ: 0,2
A601D0
Найдите тангенс угла AOB, изображённого на рисунке.
Решение:
Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=1/4=0,25.
Ответ: 0,25
51BEC9
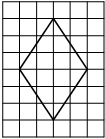
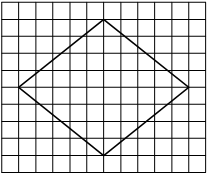
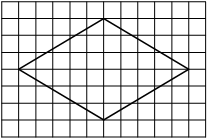
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*4=12
Ответ: 12
F519DD
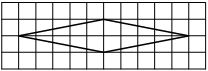
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10*2=10
Ответ: 10
704DB1
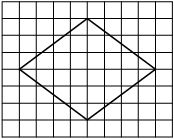
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*8=24
Ответ: 24
2F4DA5
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 6*2=6
Ответ: 6
1F239C
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 4 = 16
Ответ: 16
33E327
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 6 = 36
Ответ: 36
0B92D0
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 2 = 8
Ответ: 8
3B5D8B
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 4 = 20
Ответ: 20
CFCA33
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 8 = 40
Ответ: 40
3B008A
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 6 = 30
Ответ: 30
8372E0
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 4 = 24
Ответ: 24
FFD1EE
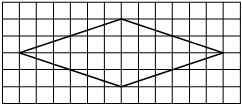
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение:
Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 2 = 12
Ответ: 12
E2A932
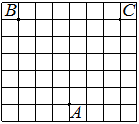
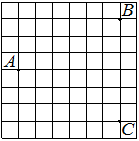
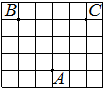
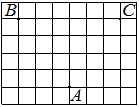
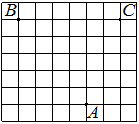
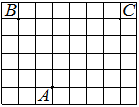
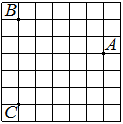
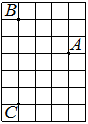
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3
969F4E
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5
AFB9A1
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1
D234F7
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2
68F679
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 4
9672D7
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5
3F311F
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6
C598DA
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 8
FCC29D
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7
0DBF9B
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6
B73FA9
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1
78BDFE
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7
CB1715
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3
107F53
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2
5B4C37
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
FEDC09
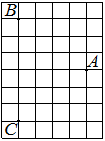
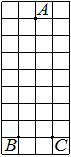
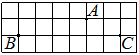
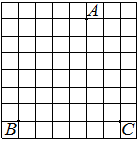
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6
C563EA
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5
B2853A
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
FE13B1
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2
C8BF73
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5
A4B62F
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2
DA3762
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 7
C576A6
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 1
9D880E
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4
078B48
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6
854014
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 3
B4DCCF
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
Решение:
Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 8
259D23
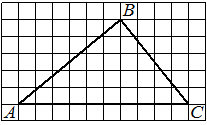
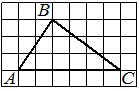
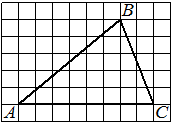
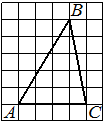
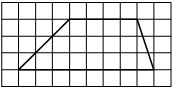
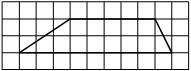
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
9C2804
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
BC4EBE
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
7ECBCE
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
D2D94B
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
8F5C52
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
686EFB
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
07C968
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
E3456A
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3
794271
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4
A1906B
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2
E52B99
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Решение:
Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5
E331C7
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6
F7FF65
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8
AAC1BC
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7
2BD44A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8
6DE9A6
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 4
39A91A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9
197283
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 5
2EA9C2
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7
ED1F0E
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9
10323E
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10
ED4E1A
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6
4FAEEC
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Решение:
Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10
F8232E
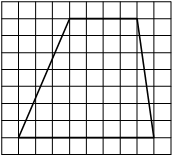
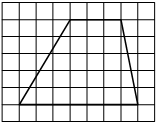
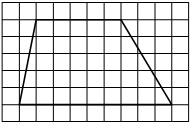
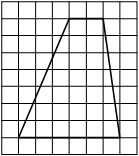
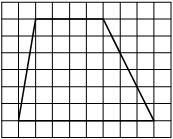
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+7) : 2 = 4
Ответ: 4
351A72
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (6+10) : 2 = 8
Ответ: 8
5EFE19
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (4+8) : 2 = 6
Ответ: 6
C05266
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+10) : 2 = 6
Ответ: 6
CFD6D8
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (3+7) : 2 = 5
Ответ: 5
3BD771
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+8) : 2 = 5
Ответ: 5
869450
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+5) : 2 = 3
Ответ: 3
19D522
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (2+6) : 2 = 4
Ответ: 4
A28F9D
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (1+9) : 2 = 5
Ответ: 5
2EF821
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (3+9) : 2 = 6
Ответ: 6
45A5FF
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (5+9) : 2 = 7
Ответ: 7
7AAADC
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.
Решение:
Длина средней линии трапеции равна полусумме её оснований, т. е. (4+10) : 2 = 7
Ответ: 7
321F00
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
87C214
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6
6CB64A
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
4801B0
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
DEA70E
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
6D0D8F
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
8D9098
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8
90A16B
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
F3D7EA
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
35106F
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10
1C594B
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6
E4F439
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
Решение:
Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12
657F97
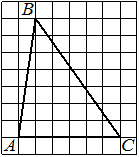
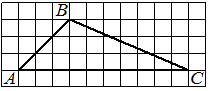
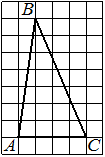
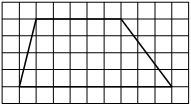
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 3 = 9
Ответ: 9
E873D3
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 5 = 20
Ответ: 20
9E69AF
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 3 = 12
Ответ: 12
53C928
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 5 = 15
Ответ: 15
EE2C25
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 10 = 25
Ответ: 25
1B4EAF
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 9 = 36
Ответ: 36
94B40E
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 4 = 10
Ответ: 10
F50FF8
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 6 = 21
Ответ: 21
3A7F81
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 4 * 3 = 6
Ответ: 6
DFB4EA
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 8 = 28
Ответ: 28
7AEBD7
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 10 * 7 = 35
Ответ: 35
4718F7
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Решение:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 2 = 14
Ответ: 14
0C5645
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (7+3) * 4= 20
Ответ: 20
695D77
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 7= 42
Ответ: 42
07B1AD
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 3 = 18
Ответ: 18
4774FE
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 2= 14
Ответ: 14
284762
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 4= 28
Ответ: 28
2916B2
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 5= 25
Ответ: 25
867701
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 5= 35
Ответ: 35
B5D99F
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 7= 28
Ответ: 28
B11571
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 6= 36
Ответ: 36
E46263
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 3= 12
Ответ: 12
283DE4
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 2= 10
Ответ: 10
383C46
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 6= 30
Ответ: 30
2E7B84
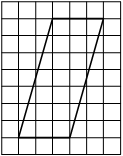
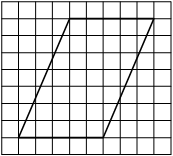
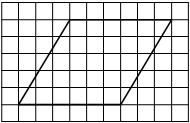
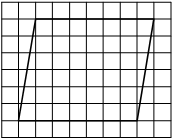
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 4 = 28
Ответ: 28
71E23E
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 2 = 10
Ответ: 10
3BD9B6
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 4 = 20
Ответ: 20
5C5046
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 3 = 18
Ответ: 18
566A4E
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 6 = 36
Ответ: 36
0275CC
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 3 * 7 = 21
Ответ: 21
E81F8D
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 7 = 35
Ответ: 35
2A59D7
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 2 = 14
Ответ: 14
5FC71A
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 5 = 30
Ответ: 30
257B6F
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 6 = 42
Ответ: 42
839354
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 4 * 3 = 12
Ответ: 12
C1A1AF
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
Решение:
Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 5 = 25
Ответ: 25
9B4AE0
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 14
11403B
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 8
CDF457
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 15
06B968
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 10
AFB70E
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 13
C4025D
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 16
E4CBB2
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 9
211628
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 17
5D3FCF
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 19
320729
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 18
C72856
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 12
BB2950
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Решение:
Считаем клетки внутри фигуры.
Ответ: 11
F78C61
Вычисление площадей фигур на клетчатой бумаге разными способами
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Авдеева Е.А. 1
1МБОУ «Карагайская средняя общеобразовательная школа №1»
Ашмарина Н.С. 1
1МБОУ «Карагайская средняя общеобразовательная школа №1»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Ещё в начальной школе мы освоили формулы нахождения площадей прямоугольника S = a • b, квадрата S = a2 и прямоугольного треугольника
S = (a • b) : 2.
При изучении математики в 5 классе мы тоже применяли эти формулы для вычисления площадей фигур. А также освоили основные свойства площадей: равные фигуры имеют равные площади; площадь фигуры равна сумме площадей её частей. В учебнике по математике для 5 класса есть задачи на клетчатой бумаге на нахождение площадей фигур. [1]
Мне стало очень интересно, какие способы решения таких задач существуют. При изучении литературы выявилось, что их достаточное количество. Я решила изучить их и проверить какой из них самый результативный, т.е. малозатратный по времени и дает безошибочный результат.
Проблема: Существует ли самый результативный способ нахождения площади фигуры на клетчатой бумаге?
Гипотеза: Самым эффективным способом вычисления площадей на клетчатой бумаге будет способ по формуле Пика.
Цель работы: Изучить способы решения задач на клетчатой бумаге и выбрать самый наилучший.
Задачи:
- Изучить литературу по теме исследования.
- Выбрать и изучить способы нахождения площадей фигур на клетчатой бумаге.
- Подобрать задачи.
- Провести эксперимент.
- Сделать выводы.
Объект исследования: фигуры на клетчатой бумаге.
Предмет исследования: площадь фигур.
Методы исследования:
1) теоретический – изучение литературы;
2) эмпирический – эксперимент, анализ, сравнение;
3) математический – построение таблиц, вычисления.
Актуальность данной темы выбрана желанием показать разнообразие способов решения одной задачи. При решении олимпиадных задач я часто находилась в затруднении при встрече с задачами на клетчатой бумаге. А увидев такие задачи в КИМах ЕГЭ, ОГЭ приняла решение исследовать задачи на клетчатой бумаге и помочь выпускникам освоить их, чтобы как можно меньше времени тратить на выполнение таких заданий.
Рассмотрим основные способы решения таких задач в исследовательской работе.
Основная часть
2.1 Площадь фигуры как сумма площадей её частей
Задача 1. Найдём площадь фигуры АВСD (см.рис.1). Если клетки размером 1х1см.
Разобьем фигуру АВСD на части (1 и 2).
По свойству площадей:
S = S1 + S2 = (2•3):2 + 3•2 = 3 + 6 = 9 см²
Ответ: 9 см²
Рис.1
Задача 2. Найдём площадь фигуры АВСD (см.рис.2). Если клетки размером 1х1см.
Разобьем фигуру АВСD на части (1, 2, 3 и 4).
По свойству площадей:
S = S1 + S2 + S3 + S4 =
= (1•4):2 + (1•3):2 + 1•1 + (1•2):2 =
= 2 + 1,5 + 1 + 1 = 5,5 см²
Ответ: 5,5 см²
Рис.2
Задача 3. Найдём площадь фигуры АВСD (см. рис.3). Если клетки размером 1х1см.
Разобьем фигуру АВСD на части (1, 2 и 3).
По свойству площадей:
S = S1 + S2 + S3 = (1•4):2 + (3•3):2 + (1•3):2 = 2 + 4,5 + 1,5 = 8 см²
Ответ: 8 см²
Рис.3
2.1 Площадь фигуры как часть площади прямоугольника
Задача 4. Найдём площадь фигуры АВСD (см. рис.4). Если клетки размером 1х1см.
Опишем около фигуры АВСD прямоугольник.
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2, 3 и 4):
S = Sпр – S1 – S2 – S3 – S4 =
= 4•4 – (3•1):2 – (3•1):2 – (3•1):2 – (3•1):2 =
=16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см2. Ответ: 10 см²
Рис.4
Задача 5. Найдём площадь фигуры АВСD (см. рис.5). Если клетки размером 1х1см.
Опишем около фигуры АВСD прямоугольник.
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2 и 3):
S = Sпр – S1 – S2 – S3 =
= 4•4 – (4•4):2 – (2•1):2 – (2•1):2 = 16 – 8 – 1 – 1 =
= 6 см². Ответ: 6 см²
Рис. 5
Задача 6. Найдём площадь фигуры АВСD (см.рис.6). Если клетки размером 1х1см.
Опишем около фигуры АВСD прямоугольник.
Из площади прямоугольника вычтем площади полученных простых фигур (1, 2, 3 и 4):
S = Sпр – S1 – S2 – S3 – S4 =
= 3•6 – (4•1):2 – (2•2):2 – (4•1):2 – (2•2):2 =
= 18 – 2 – 2 – 2 – 2 = 10 см². Ответ: 10 см²
2.3 Формула Пика
Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.
Нарисуем на листе многоугольник с вершинами в узлах (рис. 7) и найдем его площадь. [2]
Оказывается площади многоугольников, вершины которых расположены в узлах сетки, можно проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника.
Рис. 7
Рис. 8
Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рис.8). Обозначим через В — количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника вычисляется по формуле:
S = В + 4 · = В + – 1.
Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, освоили формулу S = В + – 1. Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки! Это и есть формула Пика. [5]
Она секретной не является. Информация о ней в интернете имеется. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим. Автор этой формулы австрийский математик Георг Пик (приложение 1). [2]
Можно убедиться в том, что формула Пика верна для всех рассмотренных выше примеров. Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.
Рассмотрим применение формулы Пика на примерах:
Задача 7. Найдем площадь треугольника (см. рис.9). Отметим узлы (пересечение линий) на границе треугольника и внутри треугольника:
В = 34 (обозначены черным), Г = 15 (обозначены серым).
S= 34 + 15/2 – 1 = 40,5 ед² Ответ: 40,5
Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. [7]
Рис.9
Задача 8. Вычислим площадь пятиугольника (см.рис.10).
Отметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:
В = 43 (обозначены черным),
Г = 14 (обозначены серым).
S= 43 + 14/2 – 1 = 49 ед² Ответ: 49.
Рис.10
Конечно, есть ещё способы нахождения фигур на клеточной бумаге. Например, можно просто считать количество целых клеток внутри фигуры, а из оставшихся кусочков «складывать» целые клетки, но это довольно долго и трудно, особенно если фигура сложной формы.
Можно находить площади фигур на клеточной бумаге, используя формулы площади произвольного треугольника, трапеции, ромба, параллелограмма. Но для этого нужно знать эти формулы и уметь ими пользоваться.
И есть такие фигуры на клеточной бумаге, для которых эти формулы применить очень трудно, да и затратно по времени. А на экзамене по математике в 9-м и в 11-м классе каждая минута дорога!
2.4 Эксперимент и исследование
Мы решили провести эксперимент для того, чтобы выяснить какой из рассмотренных способов является самым эффективным, т.е. результативным (решение без ошибок) и малозатратным по времени.
Обучающимся 9-го и 11-го классов (13 и 8 человек соответственно) мы показали и объяснили способы нахождения площадей фигур на клетчатой бумаге. Ученики решали задачи с помощью способов описанных в п.2.1, 2.2 (приложение 2) [3], [6], [7]. Каждому нужно было решить по четыре задачи и засечь время их выполнения.
Затем рассказали им о формуле Пика, показали на примерах её применение и предложили решить другие задачи на клетчатой бумаге, но по формуле Пика (снова засекали время).
Результаты эксперимента представлены в таблицах (приложение 3).
Общие результаты эксперимента:
|
Затраченное время — среднее значение (мин) |
Количество уч-ся, допустивших ошибки |
Безошибочных работ |
||||||||||
|
T1 |
T2 |
Т3 |
О1 |
О2 |
О3 |
Б1 |
Б2 |
Б3 |
||||
|
11 класс (13 учеников) |
2,9 |
2,8 |
2,0 |
9 |
10 |
9 |
4 |
3 |
4 |
|||
|
9 класс (8 учеников) |
2,4 |
2,3 |
1,4 |
8 |
6 |
3 |
— |
2 |
5 |
|||
|
Всего (21 ученик) |
2,7 |
2,6 |
1,7 |
17 |
16 |
12 |
4 |
5 |
9 |
Заключение
Выполненный эксперимент показал, что:
- Из двух классов почти никто не знал формулу Пика.
- 17 из 21 учащихся допустили ошибки при вычислении площадей фигур, используя одно из свойств площадей – площадь фигуры равна сумме площадей ее частей;
- 16 из 21 учащихся допустили ошибки при вычислении площадей фигур на клетчатой бумаге, используя правило площади фигуры, как части площади прямоугольника;
- 12 из 21 учащихся допустили ошибки при решении задач, используя формулу Пика;
- количество ошибок, допущенных при решении задач по формуле Пика, сократилось;
- количество безошибочных работ увеличилось;
- время, затраченное на решение по формуле Пика, сократилось.
Существует достаточное количество способов нахождения площадей фигур на клетчатой бумаге. Мы рассмотрели основные из них. Задачи, поставленные в самом начале нашей работой, выполнили. Все способы нахождения площадей фигур на клетчатой бумаге хороши, но самым результативным оказался способ решения по формуле Пика!
Наша гипотеза подтвердилась. А тем выпускникам, которые недостаточно знают формулы площадей фигур или имеют проблемы с геометрией, эта работа – неоспоримая помощь в подготовке к выполнению таких заданий.
Список использованных источников и литературы
- Виленкин В.Я. Математика 5 класс: учебник для учащихся общеобразовательных школ / В.Я. Виленкин. – М. : Мнемозина, 2016. – 280 с.
- Смирнова И.М. Геометрия на клетчатой бумаге: учебно-методическое пособие / И.М. Смирнова, В.А. Смирнов – М: Чистые пруды, 2009. – 32 с.
- Смирнова И.М. Геометрические задачи с практическим содержанием: пособие для учащихся / И.М. Смирнова, В.А. Смирнов – М.: Чистые пруды, 2010. – 136 с.
- Википедия. Пик. Георг. [Электронный ресурс]. – Режим доступа: https://ru.wikipedia, свободный. – Загл. с экрана.
- Жарковская Н.М., Рисс Е.А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17. – [Электронный ресурс]. – Режим доступа: http://mat.1september.ru/2009/23/gazeta_23_09.pdf, свободный. – Загл. с экрана.
- ФИПИ. Открытый банк заданий ЕГЭ 2017-2018 по математике. – [Электронный ресурс]. – Режим доступа: http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege, свобоный. – Загл. с экрана.
- Математика? Легко!!! Площади фигур. – [Электронный ресурс]. – Режим доступа: https://matematikalegko.ru/category/plocshadi-figur, свободный. – Загл. с экрана.
- Фигуры на квадратной решётке — «РЕШУ ОГЭ»: математика. ОГЭ — [Электронный ресурс]. – Режим доступа: https://oge.sdamgia.ru/test?theme=14, свободный. Загл. с экрана.
Приложение 1
Георг Алекса?ндр Пик (нем. Georg Alexander Pick; 10 августа 1859 г. – 13 июля 1942 г.) – австрийский математик. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. 16 апреля 1880 года под руководством Лео Кёнигсбергера Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо было пройти хабилитацию. Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифферен-циальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца-Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [4]
Приложение 2
Вычислить площадь фигуры, используя одно из свойств площадей – площадь фигуры равна сумме площадей ее частей.
- Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
- Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
Вычислить площадь фигуры, используя правило пощади фигуры как части площади прямоугольника.
- Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
- Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
- Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
Вычислить площадь фигуры, используя формулу Пика.
- Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
- Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
- Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
- Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.
Приложение 3
Результаты эксперимента в 9-м классе:
|
Затраченное время |
Количество ошибок |
|||||||
|
T1 |
T2 |
T3 |
О1 |
О2 |
О3 |
|||
|
1/9 |
2,1 |
2,57 |
2,0 |
3 |
2 |
4 |
||
|
2/9 |
1,09 |
2,36 |
1,28 |
3 |
3 |
4 |
||
|
3/9 |
1,38 |
2,15 |
1,20 |
3 |
1 |
2 |
||
|
4/9 |
0,51 |
1,10 |
0,50 |
1 |
1 |
|||
|
5/9 |
6,10 |
3,50 |
2,01 |
2 |
1 |
|||
|
6/9 |
1,10 |
— |
1,03 |
2 |
4 |
|||
|
7/9 |
1,13 |
1,52 |
0,55 |
2 |
||||
|
8/9 |
5,35 |
1,45 |
2,20 |
2 |
||||
|
Всего (8 учеников) |
2,4 |
2,3 |
1,4 |
8 |
6 |
3 |
Индекс 1 – решение задач, используя одно из свойств вычисления площадей – площадь фигуры равна сумме площадей ее частей.
Индекс 2 – решение задач, используя правило площади фигуры, как части площади прямоугольника.
Индекс 3 – решение задач по формуле Пика.
Результаты эксперимента в 11-м классе:
|
Затраченное время |
Количество ошибок |
|||||||
|
T1 |
T2 |
T3 |
О1 |
О2 |
О3 |
|||
|
1/11 |
1,00 |
1,30 |
1,00 |
|||||
|
2/11 |
4,55 |
3,15 |
2,10 |
4 |
1 |
|||
|
3/11 |
3,10 |
4,00 |
2,08 |
4 |
3 |
|||
|
4/11 |
2,55 |
3,33 |
2,12 |
1 |
1 |
|||
|
5/11 |
2,39 |
2,20 |
2,03 |
1 |
1 |
|||
|
6/11 |
2,58 |
1,44 |
1,10 |
2 |
3 |
|||
|
7/11 |
1,59 |
2,28 |
3,03 |
2 |
2 |
1 |
||
|
8/11 |
3,30 |
3,45 |
2,50 |
1 |
3 |
4 |
||
|
9/11 |
3,50 |
2,44 |
2,05 |
3 |
2 |
1 |
||
|
10/11 |
3,50 |
4,00 |
1,10 |
4 |
2 |
4 |
||
|
11/11 |
2,07 |
3,21 |
1,30 |
2 |
3 |
|||
|
12/11 |
3,58 |
2,06 |
3,08 |
2 |
1 |
|||
|
13/11 |
4,15 |
3,20 |
3,28 |
3 |
1 |
|||
|
Всего (13 учеников) |
2,9 |
2,8 |
2,0 |
17 |
16 |
12 |
Индекс 1 – решение задач, используя одно из свойств вычисления площадей – площадь фигуры равна сумме площадей ее частей.
Индекс 2 – решение задач, используя правило площади фигуры, как части площади прямоугольника.
Индекс 3 – решение задач по формуле Пика.
Просмотров работы: 1515