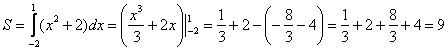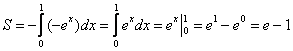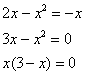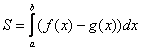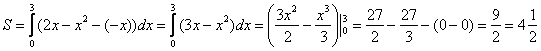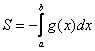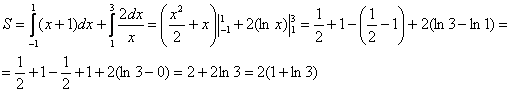Как найти площадь графика производной

Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:

Пример 10
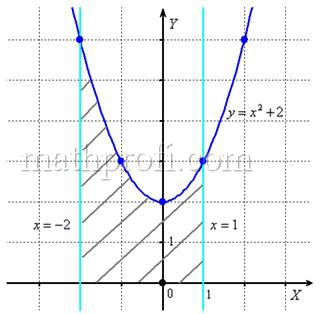
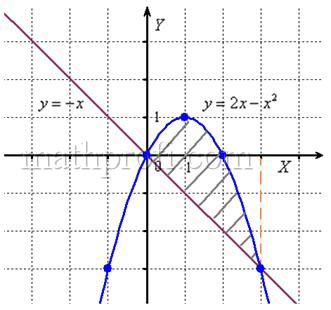
Вычислить площадь фигуры, ограниченной линиями .

И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.

В нашей задаче: прямая  определяет ось , прямые  параллельны оси  и парабола  симметрична относительно оси , для неё находим несколько опорных точек:

Искомую фигуру желательно штриховать:

Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке   график функции  расположен над осью , поэтому искомая площадь:

Ответ:

После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.

И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

Пример 11
Вычислить площадь фигуры, ограниченной линиями  и осью

Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :

Пример 12
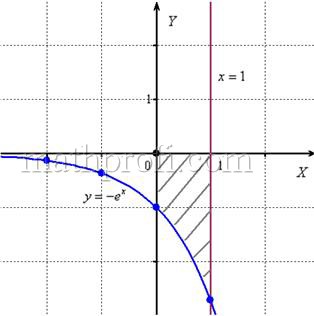
Вычислить площадь фигуры, ограниченной линиями ,  и координатными осями.

Решение: найдём несколько опорных точек для построения экспоненты:

и выполним чертёж, получая фигуру площадью около двух клеток:

Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле: .
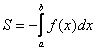
В данном случае:

Ответ:  – ну что же, очень и очень похоже на правду.

На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:

Пример 13
Найти площадь плоской фигуры, ограниченной линиями , .

Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы  и прямой , поскольку здесь будут находиться пределы интегрирования.  Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:

таким образом:

Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».

С прямой  всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
 – именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:

Выполним чертеж:

А теперь рабочая формула: если на отрезке  некоторая непрерывная функция  больше либо равна непрерывной функции , то площадь фигуры, ограниченной графиками этих функций и отрезками прямых , можно найти по формуле:

Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.

В нашем примере очевидно, что на отрезке  парабола располагается выше прямой, а поэтому из  нужно вычесть

Завершение решения может выглядеть так:

На отрезке : , по соответствующей формуле:

Ответ:

Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 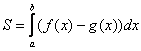. Поскольку ось  задаётся уравнением , то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу  либо

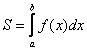
А сейчас пара типовых задач для самостоятельного решения

Пример 14
Найти площадь фигур, ограниченных линиями:

а) , .

б) , ,

Решение с чертежами и краткими комментариями в конце книги

В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:

Пример 15
Вычислить площадь фигуры, ограниченной линиями

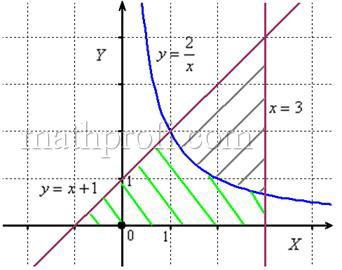
Решение: выполним бесхитростный чертёж,

хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую  можно недочертить до оси , и тогда мы вовсе не увидим нужную фигуру.

Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:

1) на отрезке  над осью  расположен график прямой ;
2) на отрезке  над осью  расположен график гиперболы .

Совершенно понятно, что площади можно (и нужно) сложить:

Ответ:

И познавательный пример для самостоятельного решения:

Пример 16
Вычислить площадь фигуры, ограниченной линиями , ,  и координатными осями.

Итак, систематизируем важные моменты этой задачи:

На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс  зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.

Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.

Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой  и прямой , где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:

и находим его корни:
 – нижний предел интегрирования,  – верхний предел.

Во-вторых, не всегда понятен «внешний вид» линии, и функция  (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html

После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.

Составляем определённый интеграл или несколько интегралов по формуле 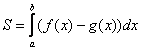, все основные вариации мы разобрали выше.

Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.

Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!

1.9. Объём тела вращения

1.7. Геометрический смысл определённого интеграла

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Содержание:

1. Примеры с решением

Пусть требуется найти площадь фигуры, ограниченной графиками функций и . Площадь требуемой фигуры на рисунке можно найти, вычитая из площади площадь

Каждую площадь можно вычислить как определенный интеграл на заданном промежутке.

Эти суждения можно обобщить следующим образом.

Так как функции и непрерывны на отрезке и на этом отрезке выполняется условие (т.е.график функции ) расположен выше графика функции то площадь ограниченная графиками функций и прямыми можно выразить следующим выражением:

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Графики функций не имеют общих точек.

Примеры с решением

Пример 1.

Найдите площадь, ограниченную графиками функций и и прямыми

Решение:

=

Графики функций пересекаются в двух точках.

Пример 2.

Найдите площадь, ограниченную графиками функций

Решение:

Найдем абсциссы точек пересечения графиков функций.

Полученные значения являются границами определенного интеграла.

Возможно вам будут полезны данные страницы:

Пример 3.

Найдите площадь, заключенную между графиками функций и

Решение:

Найдем абсциссы точек пересечени графиков.

Значит, графики пересекаются в точках с абсциссами По графикам функций также видно, что площадь, которую мы должны найти, состоит из площади, ограниченной графиками на промежутке и на промежутке На промежутке выполняется условие на промежутке выполняется условие (разность функций учитываются при записи интеграла).

! Вычислите требуемую площадь при помощи интеграла

Какой результат вы получили?

Пример 4.

Члены школьного клуба юных конструкторов работают над созданием нового двигателя для автомобиля, который будет меньше засорять окружающую среду. Для нового мотора изменение количества частиц (млрд), загрязняющих атмосферу, в год можно выразить следующим образом: Количество загрязняющих частиц, выбрасывамых старым мотором имеет вид:

a) В какой год они будут выбрасывать в атмосферу одинаковое количество частиц?

b) Какова разница между количеством вредных частиц, выброшенных в атмосферу, за этот период

Решение:

а) при удовлетворяющего условию количество вредных частиц будет одинаково.

Значение не соответствует смыслу задачи. На 3-ий год новый мотор будет давать такое же количество вредных частиц, как и старый. b) Разность количества вредных частиц равна разности площадей на промежутке [0;3].

(млрд. частиц)

Пример 5.

Вычислить площадь фигуры, ограниченной параболой и окружностью

Решение:

Сначала схематически изобразим эту площадь. Из рисунка видим

что заданные кривые ограничивают две различающиеся плоские фигуры (меньшую и большую). Каждая из этих фигур, в свою очередь, состоит из двух симметричных относительно оси частей.

Поэтому достаточно вычислить площадь верхней части каждой фигуры и затем умножить ее на два.

Найдем сначала площадь меньшей фигуры. Преобразуем уравнение окружности и определим координаты ее центра и величину радиуса.

Следовательно, центр окружности находится в точке а ее радиус Найдем точки и пересечения обеих линий, решая систему двух

уравнений

Найдем уравнение границы (части окружности) Из условия на ординаты точек границы имеем

по этой же причине уравнение нижней части границы на отрезке

По формуле (1) находим

но

— это площадь четверти окружности. Площадь всей окружности равна Второй интеграл легко вычисляется Теперь найдем искомую площадь

Теперь, чтобы найти площадь большей фигуры, необходимо из площади круга вычесть площадь меньшей фигуры:

Проверим значение первого интеграла

Обозначим

тогда при при (четвертая четверть). Поэтому

Пример 6.

Вычислить площадь фигуры, ограниченной линиями и

Решение:

Второе уравнение запишем так , отсюда следует, что это означает, что вся фигура (парабола) расположена левее точки она симметрична относительно оси так как при замене на уравнение не изменяется. Ветви параболы направлены влево; ее вершина находится в точке Определим точки ее пересечения с осью

Ветви второй параболы направлены также влево, а ее вершина совпадает с началом координат.

Определим точки пересечения этих кривых из решения системы

Одна точка пересечения вторая —

Изобразим эту фигуру на чертеже. Здесь проще вычислить площадь по формуле (2) т. е.

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

26 мая

Как за­ра­бо­тать +20–30 бал­лов на ЕГЭ бла­го­да­ря раз­бо­рам ЕГЭ с Даль­не­го Вос­то­ка

Новости

28 мая

Что сроч­но пов­то­рить к зав­траш­не­му ЕГЭ рус­ско­му язы­ку

24 мая

Обновлённая панель инструментов

22 мая

Беседы Решу ЕГЭ по подготовке к ЕГЭ

11 мая

Решение досрочных ЕГЭ по всем предметам

5 мая

Обновленный поиск заданий по ключевым словам

1 мая

Новый сервис: можно исправить ошибки!

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Из определения
производной (3) следует, что приращение
функции Δf,
обусловленное
малым приращением аргумента Δх,
можно приближенно представить в виде
Δf ≈
.
Это равенство выполняется тем точнее,
чем меньше Δх.
Если взять
бесконечно малое приращение аргумента
Δх, последнее
соотношение станет точным. Приращение
функции Δf
при этом
тоже станет бесконечно малым. Чтобы
отличать бесконечно малое (или
элементарное) приращение аргумента и
функции от конечного приращения, их
обозначают соответственно dx
и
df.
Ясно, что
элементарное приращение функции
находится по формуле

.
(7)

П р и м е р 6. Тело
брошено с начальной скоростью v₀=20,0м/с.
Его высота над уровнем земли меняется
по закону

v₀t—gt²/2
g=9,81м/с².
Определить перемещение Δh
тела за
промежуток времени Δt=10,0мс,
происшедшее
после первой секунды движения.

Считая Δt
малым, найдем
Δh
по приближенной формуле

(v₀—gt)Δt=(20,0-9,81·1,00)·0,01=0,1019м.

Точное вычисление
по формуле

дает результат Δh=0,10151м.
Отличие обоих результатов сказывается
только в четвертой значащей цифре.
Исходные данные приведены с тремя
значащими цифрами, следовательно, оба
результата практически совпадают.

6.Приближенное вычисление площади под графиком фукции.

Интегральная
сумма

На рис. 4 изображен
график функции у=f(х),
причем f(х)>0.
Требуется найти площадь фигуры,
ограниченной сверху графиком функции
f(х),
слева и справа – отрезками прямых,
проведенных через точки х=а
и х=b
параллельно оси ординат, снизу – осью
х.

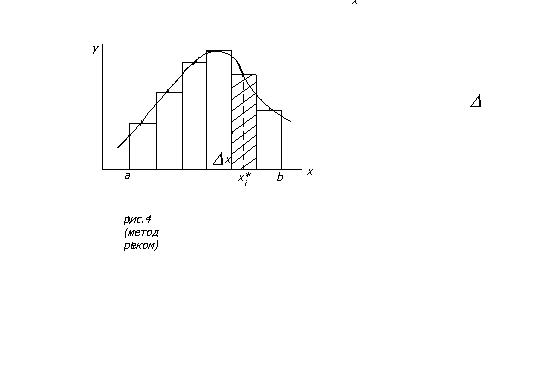
Рис.4 К понятию
определенного интеграла

Для вычисления
площади разобьем участок оси х
между точками а
и b
на n отрезков
длиной Δх₁
Δх₂…
Δх_n.
Построим n
прямоугольников с основаниями
соответственно Δх₁
Δх₂…
Δх_n
и высотами f(х₁^*),
f(х₂^*),…
f(х_n^*),
где х_i^*
— любая точка, лежащая внутри отрезка
оси х с
номером i(i=1,
2,…n). Ясно,
что искомая площадь S
приближенно равна сумме площадей
прямоугольников. Площадь прямоугольника
с номером i
очевидно равна

,
следовательно,

.
(8)

Выражение, стоящее
в правой части формулы (8), называется
интегральной суммой. Приближенное
равенство в формуле (8) будет выполняться
тем точнее, чем меньше отрезки Δх_i.

7. Точное вычисление площади под графиком функции.

Определенный
интеграл

Чтобы получить
точное выражение для площади S,
следует взять предел выражения (8),
устремив длины всех отрезков Δх_i
к нулю:

.
(9)

Очевидно, что число
слагаемых в сумме (9) при этом будет
стремиться к бесконечности.

Таким образом,
вычисление площади под графиком функции
сводится к вычислению предела от
интегральной суммы. Аналогично, вычисление
многих физических величин часто сводится
к вычислению предела некоторой
интегральной суммы. Предел интегральной
суммы (9) называется определенным
интегралом от функции f(х)
в пределах от а
до b.
Для обозначения определенного интеграла
принята запись

.
(10)

При этом полагают
по определению

=-
.

Приведем пример,
в котором необходимо использовать
понятие интеграла.

П р и м е р 7.
Известно, что плотность воздуха в
атмосфере меняется с высотой h
над уровнем моря по закону

,
где ρ₀—плотность
воздуха на уровне моря, a=Mg/RT,
M—относительная
молекулярная масса воздуха, g-ускорение
свободного падения, R-газовая
постоянная, Т-абсолютная
температура воздуха. Необходимо
определить массу воздуха в столбе
высотой Н
и площадью основания S.

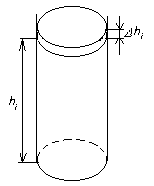
Рис.5 К примеру 7

Разобьем весь
столб воздуха на элементарные слои
толщиной Δh₁,
Δh₂,…
Δh_n,
высота i-го
слоя над уровнем моря составляет h_i
, а его объем ΔV_i=SΔh_i
(рис.5). Так как толщина слоя невелика,
можно считать, что в пределах каждого
слоя плотность воздуха практически
постоянна, поэтому масса воздуха,
заключенного в объеме ΔV_i,
составляет

,
а масса воздуха во всем столбе

.
(11)

В правой части
формулы (11) стоит интегральная сумма.
Если перейти к пределу Δh_i→0,
то приближенное равенство станет точным,
а интегральная сумма перейдет в интеграл:

.
(12)

Этот интеграл
будет вычислен в примере 9.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #