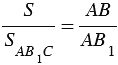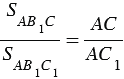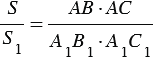Комментарии преподавателя
Повторение темы «Площадь». Решение задач
1. Повторение теоретической части главы «Площадь»
Вначале уделим внимание тому, что вспомним все основные теоремы, формулы и факты, полученные нами при изучении главы «Площадь», и акцентируем внимание на их особенностях. Затем рассмотрим сложный пример на комплексное применение нескольких из упомянутых фактов, касающихся площадей фигур.
1. Площадь квадрата равна квадрату его стороны (см. Рис. 1). 
.
Рис. 1. Квадрат
2. Площадь прямоугольника равна произведению его сторон (см. Рис. 2). 
.
Рис. 2. Прямоугольник
3. Площадь параллелограмма равна произведению основания на опущенную на него высоту (см. Рис. 3). 
.
Рис. 3. Параллелограмм
4. Площадь произвольного треугольника равна половине произведения основания на опущенную на него высоту (см. Рис. 4). 
.
Рис. 4. Произвольный треугольник
5. Площадь прямоугольного треугольника равна половине произведения катетов (см. Рис. 5). 
.
Рис. 5. Прямоугольный треугольник
6. Если у двух треугольников высоты равны (
), то их площади относятся, как основания (см. Рис. 6). 
. Полезный факт, необязательный к изучению.
Рис. 6
7. Медиана треугольника делит его на два равновеликих треугольника (см. Рис. 7). 
.
Рис. 7
8. Площадь ромба равна половине произведения диагоналей (см. Рис. 8). 
. Однако, поскольку ромб является частным случаем параллелограмма, то его площадь можно находить и по формуле площади параллелограмма.
Рис. 8. Ромб
9. Если у двух треугольников равны углы (
), то их площади относятся, как произведение сторон, заключающих данные углы (см. Рис. 9). 
. Полезный факт, не обязательный к изучению.
Рис. 9
10. Площадь трапеции равна произведению полусуммы ее оснований на высоту (см. Рис. 10). 
.
Рис. 10. Трапеция
11. Теорема Пифагора. Для прямоугольного треугольника с катетами 
и 
и гипотенузой 
квадрат гипотенузы равен сумме квадратов катетов 
(см. Рис. 11).
Теорема, обратная теореме Пифагора. Для всякой тройки положительных чисел 
, такой, что 
, существует прямоугольный треугольник с катетами 
и гипотенузой .
Рис. 11
12. Формула Герона. Применяется для нахождения площади треугольника, если известны длины его сторон (см. Рис. 12). 
, где 
полупериметр треугольника.
Рис. 12
2. Рассмотрение сложного примера
Пример 1. Через вершину прямого угла прямоугольного треугольника с катетами 6 м и 8 м проведен перпендикуляр к гипотенузе. Вычислить площади образовавшихся треугольников.
Решение. Изобразим Рис.13.
Рис. 13
Нам известно: 
высота в 
.
Найдем по теореме Пифагора гипотенузу треугольника: 
.
Для того чтобы в дальнейшем выразить высоту треугольника, вычислим его площадь с помощью катетов: 
. Выразим высоту треугольника 
из формулы площади произвольного треугольника: 
.
Рассмотрим треугольник 
(первый из тех, на которые высота разбила треугольник ). Его площадь как прямоугольного 
. Поскольку сторона 
не известна, найдем ее по теореме Пифагора: 
. Тогда 
.
Площадь треугольника 
(второго из тех, на которые высота разбила треугольник ) можно найти аналогично либо путем вычитания из площади треугольника площади треугольника . Но воспользуемся тем же методом, который мы уже применяли в этой задаче. 
прямоугольный, следовательно, 
. Найдем 
: 
. Тогда 
.
Ответ: 
; 
.
ИСТОЧНИК
http://x-uni.com/geometriya/8-klass/video/povtorenie-temy-ploschad
http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/96-test-po-geometrii-8-klass-obobshchenie-temy-ploshchad-variant-1.html
http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/97-test-po-geometrii-8-klass-obobshchenie-temy-ploshchad-variant-2.html
http://www.uchportal.ru/_ld/105/10586_zad_ploschadi.rar
http://rushkolnik.ru/tw_files2/urls_3/891/d-890061/890061_html_m5ff065f.jpg
http://cs1-48v4.vk-cdn.net/p24/3551abddfac0c8.mp3?extra=amJxaBk9gfTT0lPmsOEwb8Rn_T2twbNJH1OUazYT-T9cSSu4_1787ibMzOu6ytv1rZKrpdEq7XnWZN1f-bjAuKyWIFf7mzw
На прошлом уроке мы с вами говорили, что подобными
называются треугольники, у которых углы соответственно равны, а
сходственные стороны пропорциональны.
Число k,
равное отношению сходственных сторон подобных треугольников, называется коэффициентом
подобия.
Напомним, что подобие треугольников обозначается
следующим образом .
На этом уроке мы докажем теорему об отношении
площадей двух подобных треугольников.
Теорема. Отношение
площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство.
,
–
коэффициент подобия.
,
.
,
.
,
,
Следовательно, .
Что и требовалось доказать.
Задача. Площади подобных
треугольников и
равны
соответственно см2
и см2.
Сторона см.
Найдите сходственную ей сторону треугольника
.
Решение.
Выше мы доказали, что отношение площадей двух
подобных треугольников равно квадрату коэффициента подобия. ,
,
.
,
,
(см).
Ответ: см.
Задача. Докажите, что
отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство.
,
–
коэффициент подобия.
,
,
,
,
,
.
,
.
,
,
.
Что и требовалось доказать.
Задача. Треугольники и
подобны.
Сходственные стороны и
соответственно
равны см
и м.
Найдите отношение периметров треугольников и
.
Решение:
м
см.
.
.
Ответ: .
Итак, на этом уроке мы доказали, что отношение
площадей двух подобных треугольников равно квадрату коэффициента подобия. А
также решили несколько задач. Причём при решении одной из них установили, что
отношение периметров двух подобных треугольников равно коэффициенту подобия.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
33 379
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
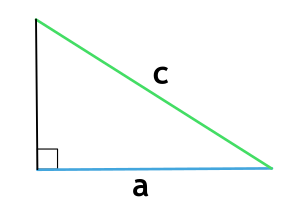
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
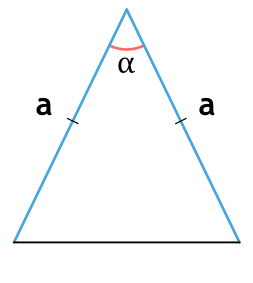
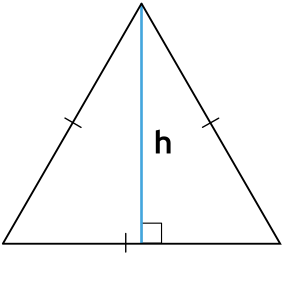
Если он равнобедренный
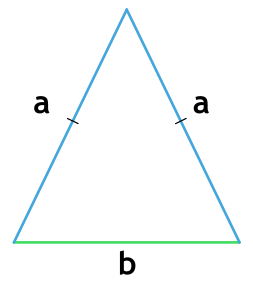
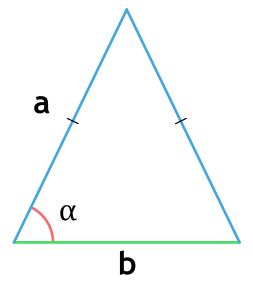
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
Если известна сторона и высота
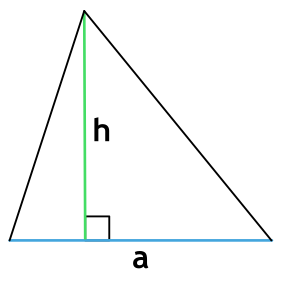
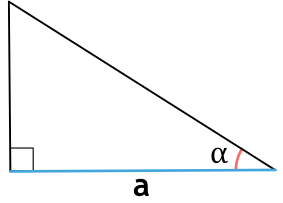
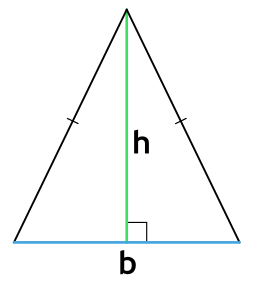
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
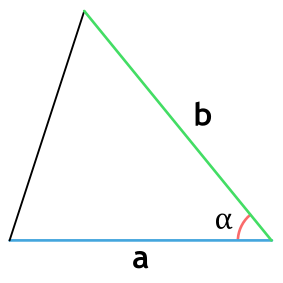
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Делайте так:
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
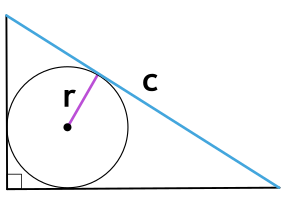
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
( 32 оценки, среднее 4.44 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь треугольника
Одну из сторон треугольника часто называют основанием. Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведенную к основанию.
Теорема
Площадь треугольника равна половине произведения его основания на высоту
Доказательство
Дано: 
АВС, СН — высота, S — площадь АВС
Доказать: S =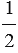 
АВ 
СН
Доказательство:
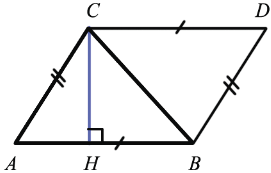
Достроим данный треугольник до параллелограмма ABCD так, как показано на рисунке. АВС = DCB (по трем сторонам (ВС — общая, AB = CD и АС = BD как противоположные стороны параллелограмма ABCD)), а у равных многоугольников равные площади, значит площади данных треугольников равны. Следовательно, площадь S — площадь АВС равна половине площади параллелограмма ABCD, т.е. S = АВ СН. Теорема доказана.
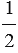
Следствие 1
Следствие 2
Если высоты двух треугольников равны, то их площади относятся как основания
Теорема
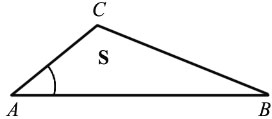
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
Доказательство
Дано: АВС, СН — высота, S — площадь АВС, А1В1С1, В1Н1 — высота, S1 — площадь А1В1С1, 
А = А1
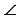
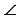
Доказать: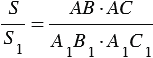 
Доказательство:
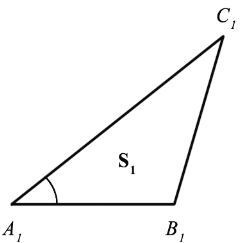
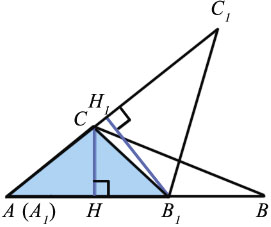
Наложим треугольник А1В1С1 на треугольник АВС так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и А1С1 наложились соответственно на лучи АВ и АС.
Треугольники АВС и АВ1С имеют общую высоту СН, поэтому
Треугольники АВ1С и АВ1С1 также имеют общую высоту — В1Н1, поэтому
Перемножая полученные равенства, находим:
или 
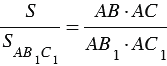
Теорема доказана.
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 515,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 571,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 4,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 838,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 841,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 867,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 947,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1208,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1243,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1277,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника — равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
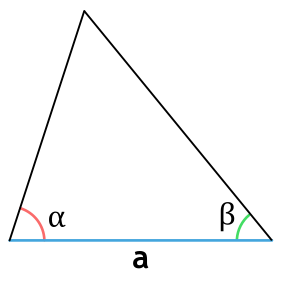
- через сторону и два прилежащих угла
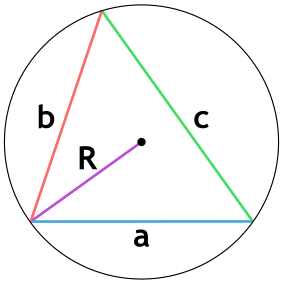
- через радиус описанной окружности и 3 стороны
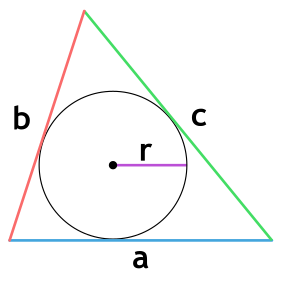
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
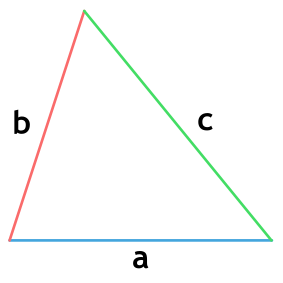
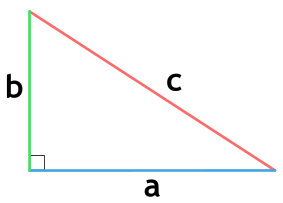
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Площадь треугольника через основание и высоту
{S = dfrac{1}{2} cdot a cdot h}
a — длина основания
h — высота, проведенная к основанию
Площадь треугольника через две стороны и угол между ними
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b — стороны треугольника
α — угол между сторонами a и b
Площадь треугольника через сторону и два прилежащих угла
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 — (alpha + beta)}
a — сторона треугольника
α и β — прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c — стороны треугольника
R — радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r cdot dfrac{a + b + c}{2}}
a, b и c — стороны треугольника
r — радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c — стороны треугольника
p — полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
Площадь прямоугольного треугольника через катеты
{S = dfrac{1}{2} cdot a cdot b}
a и b — стороны треугольника
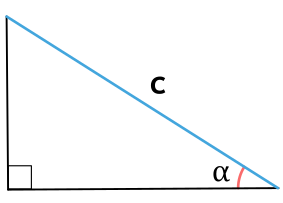
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c — гипотенуза прямоугольного треугольника
α — прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a — катет прямоугольного треугольника
α — прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r cdot (r+c)}
r — радиус вписанной окружности
c — гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 cdot c_2}
с1 и с2 — отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c — стороны треугольника
p — полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2}}
a — катет прямоугольного треугольника
c — гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
{S = dfrac{b}{4} sqrt{4a^2 — b^2}}
a — боковая сторона равнобедренного треугольника
b — основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a — боковая сторона равнобедренного треугольника
b — основание равнобедренного треугольника
α — угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
{S = dfrac{1}{2} cdot b cdot h}
b — основание равнобедренного треугольника
h — высота, проведенная к основанию равнобедренного треугольника
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a — боковые стороны равнобедренного треугольника
α — угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b — основание равнобедренного треугольника
α — угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник — треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону
{S = dfrac{sqrt{3} cdot a^2}{4}}
a — сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
{S = dfrac{h^2}{sqrt{3}}}
h — высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности
{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R — радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 sqrt{3} cdot r^2}
r — радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 — 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 — 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 — a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 — 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 — 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 — b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 — 4^2} = sqrt{4 cdot 49 — 16} = sqrt{196 — 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 — b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 — 30^2} = dfrac{30}{4} sqrt{4 cdot 289 — 900} = dfrac{30}{4} sqrt{1156 — 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .