Как найти площадь для 3 класса математика - AvtoShod.ru

Математика, 3 класс

Урок №22. Площадь прямоугольника

Перечень вопросов, рассматриваемых в теме:

Как вычислить площадь прямоугольника?
В каких единицах измеряется площадь?
Какими способами можно сравнить геометрические фигуры?

Глоссарий по теме:

Площадь – внутренняя часть любой плоской геометрической фигуры.

Квадрат – это прямоугольник, у которого все стороны равны.

Прямоугольник – это четырёхугольник, у которого все углы прямые.

Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.

2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.

3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.

Теоретический материал для самостоятельного изучения

Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.

Найдём площадь геометрической фигуры.

Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.

Найдём площадь прямоугольника со сторонами 6 см и 3 см.

Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см²

Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.

S = a ∙ b

S – площадь

a – длина

b – ширина

Задания тренировочного модуля:

1. Заполните пропуски в таблице.

а	5		6	3
b		8	9
S	15	56		24

Правильный ответ:

а	5	7	6	3
b	3	8	9	8
S	15	56	54	24

2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.

12 см; 32 см; 24 см²; 32 см²; 24; 12 см².

Правильный ответ:32см².

Источник

Главная
Справочники
Справочник по математике для начальной школы
Основы геометрии
Площадь фигуры

В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.

Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией

Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.

Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.

Сравнение площадей фигур

При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.

Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.

Сравнение площадей способом наложения

Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.

Сравнение площадей заданной меркой

Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.

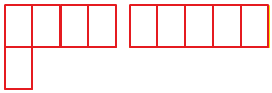
Например, меркой может быть вот такой прямоугольник :

В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.

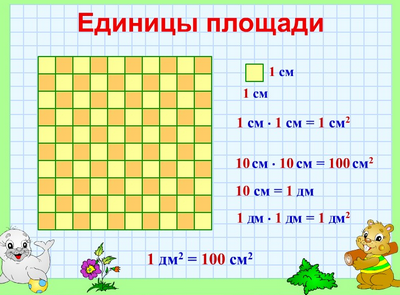
Единицы площади

В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.

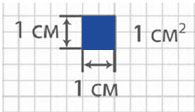
Квадратный сантиметр

Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²

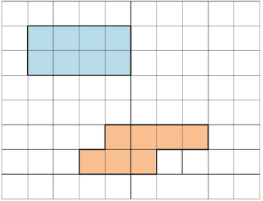
Определим площадь данных фигур:

В синей фигуре 8 см², а в красной фигуре – 7 см².

8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.

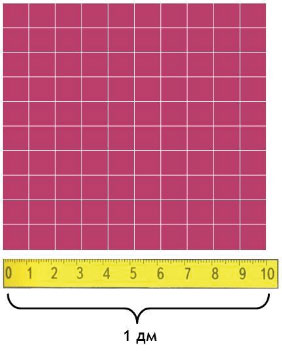
Квадратный дециметр

Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²

Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:

1 дм² = ? см²

Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть

10 • 10 = 100 см²

Значит, 1 дм² = 100 см²

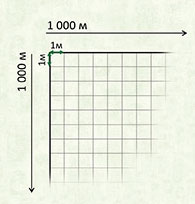
Квадратный метр

Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²

Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.

1 м² = 100 дм²

Квадратный километр

Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²

Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.

1 км² = 1000000 м²

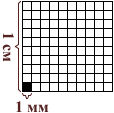
Квадратный миллиметр

Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²

Этой единицей мы пользуемся для измерения очень маленьких площадей.

1 см² = 100 мм²

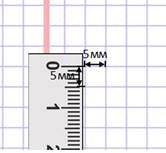
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.

Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Ар

Ар — это площадь квадрата со стороной 10 м.

Слово «ар» при числах сокращённо записывают так:

1 а, 20 а, 97 а.

1 а² = 100 м², поэтому ар часто называют соткой.

Гектар

Гектар — это площадь квадрата со стороной 100 м.

Слово «гектар» при числах сокращённо записывают так:

1 га, 20 га, 530 га.

Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.

Ар и гектар используются при измерении земельных участков.

Советуем посмотреть:

Площадь прямоугольника

Круг. Шар. Овал

Треугольники

Многоугольники

Угол. Виды углов

Обозначение геометрических фигур буквами

Периметр многоугольника

Окружность

Основы геометрии

Правило встречается в следующих упражнениях:

2 класс

Страница 43. Урок 17,
Петерсон, Учебник, часть 2

Страница 44. Урок 17,
Петерсон, Учебник, часть 2

Страница 79. Урок 32,
Петерсон, Учебник, часть 2

Страница 85. Урок 35,
Петерсон, Учебник, часть 2

Страница 91. Урок 38,
Петерсон, Учебник, часть 2

Страница 27. Урок 9,
Петерсон, Учебник, часть 3

Страница 33. Урок 11,
Петерсон, Учебник, часть 3

Страница 47. Урок 16,
Петерсон, Учебник, часть 3

Страница 51. Урок 17,
Петерсон, Учебник, часть 3

Страница 52. Урок 18,
Петерсон, Учебник, часть 3

3 класс

Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 41,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 44,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 94. Урок 35,
Петерсон, Учебник, часть 1

Страница 39. Урок 15,
Петерсон, Учебник, часть 2

4 класс

Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 65,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 53. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 78,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 32. Урок 11,
Петерсон, Учебник, часть 1

Источник

Инфоурок

›

Начальные классы

›Презентации›Презентация по математике на тему: «Площадь прямоугольника» (3 класс)

Скачать материал

аудиоформат

Сейчас обучается 121 человек из 45 регионов

Описание презентации по отдельным слайдам:

1 слайд

Урок
математики
3 класс
2 слайд

Вспоминаем то,
что важно
ПЛОЩАДЬ
3 слайд

Проблемная ситуация
4 слайд

Какой участок выбрать?
Проблемная ситуация
5 слайд

Э – хе – хе! Так не пойдет!
6 слайд

Определяем основные вопросы урока
Как быстрее найти площадь прямоугольника?
Как вычислить площадь прямоугольника, не разбивая на квадратики фигуру?
Научиться находить площадь прямоугольника новым способом
Тема урока
«Площадь прямоугольника»
7 слайд

Совместное открытие знаний
8 слайд

9 см
3 см
Совместное открытие знаний
9 • 3 = 27 см2
9 слайд

а
b
Совместное открытие знаний
S = а • b
Чтобы найти площадь прямоугольника, надо длину умножить на ширину
10 слайд

Применяем знания
Вычислите площадь синего прямоугольника по формуле.
Решение: а = 8 см, в = 4 см 8 • 4 = 32 кв.см.
Решение: а = 8 см, в = 4 см 8 • 4 = 32 кв.см.
а = 8 см
b = 4 см
S — ?
Проверьте себя!
Решение:
S= a • b
S=8 • 4 =32 (см2) -площадь прямоугольника
Ответ: S=32 см2
11 слайд

Спасибо,
ребятушки!
13 слайд

Составьте план своих действий.
Для этого выберите только необходимые действия и расставьте их по порядку.
Памятка
«Как найти площадь прямоугольника»
14 слайд

Памятка
«Как найти площадь прямоугольника»
Измерить длину прямоугольника
Измерить ширину прямоугольника
Длину умножить на ширину
Применяем знания
15 слайд

4
Применяем знания
1
1
3
2
5
1
3
4
Задание. Лесным гномам выделили под строительство домов одинаковые участки. Помоги гномам найти участки с одинаковой площадью. Раскрась их красным цветом. (Проведи необходимые измерения и вычисли площадь фигур, воспользовавшись формулой).
16 слайд

4
1
1
3
Спасибо вам, ребята!
17 слайд

«5»
«4»

Поздравляем с успешной «охотой»!

Краткое описание документа:

Тип урока: урок открытия нового знания

Форма урока: урок – исследование.

Цель урока: посредством формированияумения вычислять площадь прямоугольника с использованием формулы развивать у учащихся навыки решения простых задач на вычисление площади геометрической фигуры.

Планируемые образовательные результаты учащихся

Личностные:

• способность к милосердию (желанию помочь ближнему);

• опыт самодисциплины и самоорганизации;

• интерес к интеллектуальному творчеству.

Метапредметные:

• сотрудничество с одноклассниками в решении учебных задач;

• освоение метапредметных понятий «вычисление», «величина»;

• опыт осуществления логических операций анализа, синтеза, сравнения.

Предметные:

• умение вычислять площадь прямоугольника новым способом с использованием формулы;

• расширение опыта решения простых задач на нахождение площади геометрической фигуры.

Используемые технологии:

-проблемно – поисковый метод;

-интерактивные технологии (работа в группе, в паре);

-ИКТ.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 264 590 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

23.03.2019
500
3

23.03.2019
1113
11

23.03.2019
319
0

23.03.2019
574
2

23.03.2019
251
2

23.03.2019
2135
92

23.03.2019
1697
66

23.03.2019
245
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Организация проектно-исследовательской деятельности учащихся в рамках реализации ФГОС»
Курс повышения квалификации «Актуальные проблемы обучения детей с нарушением слуха в образовательных организациях общего и среднего профессионального образования»
Курс повышения квалификации «Сопровождение детского отдыха: от вожатого до руководителя детского лагеря»
Курс повышения квалификации «Профессиональная компетентность педагогов в условиях внедрения ФГОС»
Курс профессиональной переподготовки «Организация инклюзивного обучения в сфере образования»
Курс профессиональной переподготовки «Тьюторское сопровождение обучающихся в системе инклюзивного образования»
Курс повышения квалификации «Система работы учителя-дефектолога при обучении и воспитании детей с особыми образовательными потребностями (ООП) в общеобразовательном учреждении»
Курс повышения квалификации «Активизация познавательной деятельности младших школьников с ограниченными возможностями здоровья (ОВЗ) как стратегия повышения успешной учебной деятельности»
Курс повышения квалификации «Применение современных педагогических технологий в образовательном процессе в условиях реализации ФГОС»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс повышения квалификации «Разработка адаптированных образовательных программ в условиях ФГОС СПО»
Курс повышения квалификации «Применение методов арт-терапии в работе со старшими дошкольниками и младшими школьниками»
Курс повышения квалификации «Организация работы с обучающимися с ограниченными возможностями здоровья (ОВЗ) в соответствии с ФГОС»
Курс повышения квалификации «Система диагностики предметных и метапредметных результатов в начальной школе»

Настоящий материал опубликован пользователем Пожарникова Наталья Евгеньевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 6 лет и 7 месяцев
- Подписчики: 0
- Всего просмотров: 9603
- Всего материалов:
  
  3

Источник

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Периметр – сумма длин всех сторон фигуры.

Нахождение периметра

Р ф. = а + b + c + …

Р пр. = (а + b) · 2

Р кв. = а · 4

Чтобы найти площадь фигуры, надо длину умножить на ширину.

Нахождение площади

S пр. = а · b

S кв. = а · а

Источник

Дата публикации: 08 апреля 2017.

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P_ABCD, где А, В, С, D – это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P_ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P_ABCD.

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.

2. Напишем формулу для расчета периметра данного прямоугольника:

P_ABCD = 2 * (AB + BС)

3. Подставим в формулу наши данные:

P_ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P_ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P_ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P_ABCD= 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P_ABCD = 4 * AB

3. Подставим в формулу наши данные:

P_ABCD = 4 * 6 см = 24 см

Ответ: P_ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры.
Площадь измеряется квадратными единицами длины: см², м², дм² и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S.

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.

Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S_AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S_AKMO= AK * KM = 7 см * 2 см = 14 см².

Ответ: 14 см².

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.

В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S_AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S_AKMО = AK * KM = 8 см * 8 см = 64 см²

Ответ: 64 см².

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Источник

Сравнение площадей фигур

Сравнение площадей способом наложения

Сравнение площадей заданной меркой

Единицы площади

Квадратный сантиметр

Квадратный дециметр

Квадратный метр

Квадратный километр

Квадратный миллиметр

Ар

Гектар

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Описание презентации по отдельным слайдам:

Краткое описание документа:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

Что такое прямоугольник и квадрат

Что такое периметр прямоугольника? Формула расчета периметра

Формула расчета периметра квадрата

Задачи на нахождение периметра прямоугольника

Где используется расчет периметра прямоугольника?

Что такое площадь прямоугольника?

Формула вычисления площади квадрата

Задачи на нахождение площади прямоугольника и квадрата

Не пропустите также: