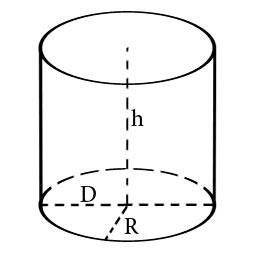
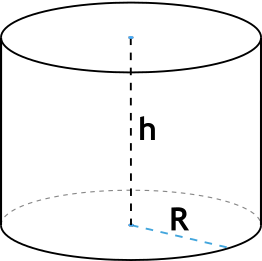
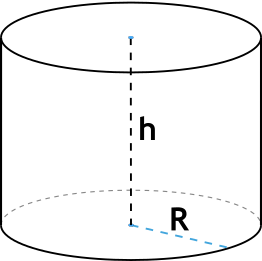
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
-
Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
При помощи нашего калькулятора вы легко сможете узнать площадь цилиндра. Так же если вам необходимо узнать площадь бочки, круглой цистерны, круглого бака и т.д., то это калькулятор то, что Вам нужно.
|
|
|
| Вычислить площадь цилиндра через: | |
| Вычислить: | |
| Длина радиуса R: | |
| Высота цилиндра h: |
Для того что бы вычислить площадь цилиндра необходимо знать его высоту и радиус или диаметр. Если нам известны указанные величины, для нас не составит труда вычислить площадь.
Полная площадь цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
S=2πR(h+R)
- Если нам известен диаметр:
S=πD(h+D/2)
Площадь боковой поверхности цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
S=2πRh
- Если нам известен диаметр:
S=πDh
Где S – площадь, R – радиус, D – диаметр, h — высота, π – число Пи которое всегда примерно равно 3,14.
Чтобы найти площадь поверхности цилиндра необходимо знать радиус его основания и высоту. Очень важно понимать, что существует две поверхности — боковая и полная. Площадь боковой поверхности включает в себя площадь поверхности цилиндра без учета площади его оснований. Полная же площадь основания цилиндра включает как площадь боковой поверхности, так и обоих оснований цилиндра.
На нашем сайте вы можете рассчитать и объем цилиндра
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые её пересекают.
Содержание:
- калькулятор площади поверхности цилиндра
- формула площади поверхности цилиндра
- формула площади боковой поверхности цилиндра
- примеры задач
Формула площади поверхности цилиндра
{S_{полн} = 2pi R(h+R)}
R — радиус основания цилиндра
h — высота цилиндра
Формула площади боковой поверхности цилиндра
{S_{бок} = 2pi Rh}
R — радиус основания цилиндра
h — высота цилиндра
Примеры задач на нахождение площади поверхности цилиндра
Задача 1
Найдите площадь поверхности цилиндра если его высота равна 5см а радиус 6см.
Решение
Так как необходимо найти площадь полной поверхности цилиндра, воспользуемся первой формулой. Подставим в нее значения из условия и произведем вычисления.
S_{полн} = 2pi R(h+R) = 2pi cdot 6(5+6) = 12pi cdot 11 = 132 pi : см^2 approx 414.69023 : см^2
Ответ: 132 pi : см^2 approx 414.69023 : см^2
Чтобы проверить правильность ответа можно использовать калькулятор .
Задача 2
Найдите площадь боковой поверхности цилиндра, если радиус основания равен 2см а высота 7см.
Решение
Для решения этой задачи нам потребуется вторая формула.
S_{бок} = 2pi Rh = 2pi cdot 2 cdot 7 = 28 pi : см^2 approx 87.96459 : см^2
Ответ: 28 pi : см^2 approx 87.96459 : см^2
Осталось убедиться, что задача решена верно, для этого используем калькулятор .
Площадь поверхности цилиндра
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности цилиндра
Чтобы посчитать площадь поверхности цилиндра воспользуйтесь нашим очень удобным онлайн калькулятором:
Площадь боковой поверхности
Высота цилиндра h =
=
Площадь боковой поверхности цилиндра Sбпц =
0
Округление ответа: Округление числа π:
Площадь полной поверхности
Высота цилиндра h =
=
Площадь полной поверхности цилиндра Sппц =
0
Округление ответа: Округление числа π:
Просто введите данные и получите ответ.
Теория
Площадь боковой поверхности цилиндра
Как вычислить площадь боковой поверхности цилиндра Sбпц, зная высоту цилиндра h и его радиус r (или диаметр d)?
Формулы
Через радиус:
Sбпц = 2⋅π⋅r⋅h
Через диаметр:
Sбпц = π⋅d⋅h
Пример #1
К примеру, посчитаем площадь боковой поверхности цилиндра с высотой 5 см и радиусом 1.5 см:
Sбпц = 2 ⋅ 3.14 ⋅ 1.5 ⋅ 5 = 6.28 ⋅ 7.5 = 47.1 см²
Пример #2
Посчитаем площадь боковой поверхности цилиндра с высотой 10 см и диаметром 4 см:
Sбпц = 3.14 ⋅ 4 ⋅ 10 = 125.6 см²
Площадь полной поверхности цилиндра
Как вычислить площадь полной поверхности цилиндра Sппц, зная высоту цилиндра h и его радиус r (или диаметр d)?
Формулы
Через радиус:
Sппц = 2⋅π⋅r⋅(h+r)
Через диаметр:
Sппц = π⋅d²2 + π⋅d⋅h
Пример #1
К примеру, посчитаем площадь полной поверхности цилиндра с высотой 8 см и радиусом 2 см:
Sппц = 2 ⋅ 3.14 ⋅ 2 ⋅ (8+2) = 6.28 ⋅ 2 ⋅ 10 = 125.6 см²
Пример #2
Посчитаем площадь полной поверхности цилиндра с высотой 2 м и диаметром 0.5 м:
Sппц = 3.14⋅0.5²2 + 3.14⋅0.5⋅2 = 0.3925 + 3.14 = 3.5325 м²
См. также
Как рассчитать площадь цилиндра
На данной странице калькулятор поможет рассчитать площадь поверхности цилиндра онлайн. Для расчета задайте высоту и радиус.
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Боковая поверхность
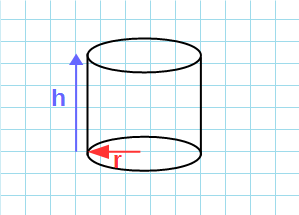
Формула площадь боковой поверхности цилиндра через высоту и радиус:
π — константа равная (3.14); r — радиус основания; h — высота цилиндра.
Полная поверхность

Формула площадь полной поверхности цилиндра через высоту и радиус:
π — константа равная (3.14); r — радиус основания; h — высота цилиндра.