Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
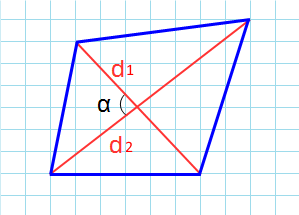
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
d1, d2 — диагонали; α — угол между диагоналями.
Через стороны и противолежащие углы
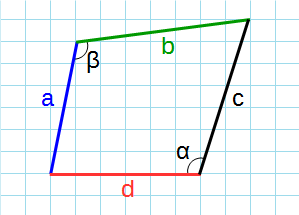
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника; α, β — противолежащие углы.
Площадь вписанного четырехугольника в окружность
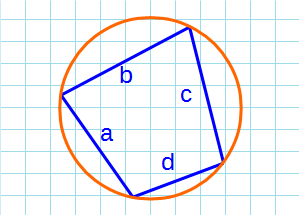
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника.
Площадь описанного четырехугольника около окружности через радиус
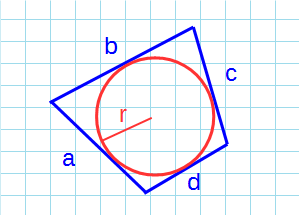
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
p — полупериметр четырехугольника; r — радиус вписанной окружности; a, b, c, d — стороны четырехугольника.
Площадь описанного четырехугольника около окружности через стороны и противолежащие углы
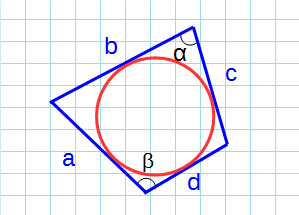
Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы:
p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника; α, β — противолежащие углы.
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
-
Расчет площади
- 1. Через диагонали и угол между ними
- 2. По всем сторонам (формула Брахмагупты)
- 3. Через полупериметр и радиус вписанной окружности
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
3. Через полупериметр и радиус вписанной окружности
Формула расчета
S = p ⋅ r
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Калькулятор расчета площади четырехугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  |
S = ab | |
 |
|||
 |
|||
| Параллелограмм |  |
||
 |
|||
 |
|||
| Квадрат |  |
S = a 2 | |
 |
S = 4r 2 | ||
 |
|||
 |
|||
| Ромб |  |
||
 |
|||
 |
|||
 |
|||
 |
|||
| Трапеция |  |
||
 |
S = m h | ||
 |
|||
 |
|||
| Дельтоид |  |
S = ab sin φ | |
 |
 |
||
 |
|||
 |
|||
| Произвольный выпуклый четырёхугольник |  |
||
| Вписанный четырёхугольник |  |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
 |
|
 |
|
 |
|
| Параллелограмм | |
 |
|
 |
|
 |
|
| Квадрат | |
 |
S = a 2
где |
 |
S = 4r 2 |
 |
|
 |
|
| Ромб | |
 |
|
 |
|
 |
|
 |
|
 |
|
| Трапеция | |
 |
|
 |
|
 |
|
 |
|
| Дельтоид | |
 |
|
 |

где |
 |
|
 |
|
| Произвольный выпуклый четырёхугольник | |
 |
|
| Вписанный четырёхугольник | |
 |
| Прямоугольник |
 |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Квадрат
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
Ромб
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
Дельтоид
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
Произвольный выпуклый четырёхугольник
φ – любой из четырёх углов между ними
Вписанный четырёхугольник
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
http://www.resolventa.ru/spr/planimetry/sqf.htm
Area of a quadrilateral is the space inside the boundary of a quadrilateral or in other words, the space enclosed by the edges of a quadrilateral. A quadrilateral can be defined as a closed two-dimensional shape that has four sides or edges, and also four corners or vertices. In mensuration, the shape of objects is classified based on the number of sides of the polygon. For example, a shape with three edges is a triangle, a shape with four edges is a quadrilateral, a shape with five edges is a pentagon, and so on. Quadrilaterals or any polygons can be classified into two categories, regular quadrilaterals/polygons i.e., all sides are of equal length, and irregular quadrilaterals i.e., all sides are not equal.
What is a Quadrilateral?
A quadrilateral is a polygon with four sides. A closed two-dimensional figure, formed by joining the four non-collinear points is called a quadrilateral. A quadrilateral has four sides, four angles, and four vertices. The sides of the quadrilateral may or may not be equal. Various types of quadrilaterals can be defined based on the properties of their angles, sides, and diagonals, some of which are as follows:
- Rectangle
- Square
- Rhombus
- Parallelogram
- Trapezium
- Kite
Properties of Quadrilateral
All quadrilaterals have some common properties that are as follows:
- A closed figure has four sides.
- The summation of the Interior angles of a quadrilateral is 360 degrees.
- The four sides can vary in length or maybe equal depending upon the type of quadrilateral.
What is the Area of Quadrilateral?
Area of a quadrilateral is the space enclosed by all the boundaries of a quadrilateral. Area of a quadrilateral is measured in square units such as m2, in2, cm2, etc. Area of a regular quadrilateral is calculated by using different formulas. For calculating the area of irregular quadrilateral various formulas are used which are discussed below in this article.
Area of Quadrilateral Formula by Dividing it into Two Triangles
In a quadrilateral ABCD, the length of the diagonal BD is ‘d’. ABCD can be divided into two triangles Δ ABD, and Δ BCD by the diagonal BD. For calculating the area of the quadrilateral ABCD we calculate the area of individual triangles and add them accordingly. But for calculating area of a triangle, its height must be known. Let us assume that the heights of the triangles ABD and BCD be h1 and h2 respectively.
Area of the triangle ABD = (1/2) × d × h1.
Area of the triangle BCD = (1/2) × d × h2.
From the figure, the area of the quadrilateral ABCD = area of ΔABD + area of ΔBCD.
Area of the quadrilateral ABCD = (1/2) × d × h1+ (1/2) × d × h2 = (1/2) × d ×( h1+h2 ).
Thus, the formula used to find the area of a quadrilateral is,
Area of Quadrilateral = (1/2) × Diagonal × (Sum of heights) = (1/2) × d ×( h1+h2 )
Area of Quadrilateral with Vertices
If vertices of a quadrilateral are given then its area is calculated by the given formula. Suppose A(x1, y1), B(x2, y2), C(x3, y3), and D(x4, y4) be the vertices of a quadrilateral ABCD.
Then its area is calculated by using two different methods which are discussed below:
Area of Quadrilateral Using Coordinates
Follow the directions of the arrow, and add the diagonal products, i.e., x1y2, x2y3, x3y4, and x4y1.
(x1y2 + x2y3 + x3y4 + x4y1)….(i)
Now, follow the dotted arrows and add the diagonal products, i.e., x2y1, x3y2, x4y3, and x1y4.
(x2y1 + x3y2 + x4y3 + x1y4)….(ii)
Now, subtract equation (ii) from (i) and multiply the result by 1/2.
(1/2) × [(x1y2 + x2y3 + x3y4 + x4y1) – (x2y1 + x3y2 + x4y3 + x1y4)]
Thus, the formula for the area of the quadrilateral when vertices are given:
Area of Quadrilateral Using Area of Triangle
For this method, we divide the given quadrilateral into two triangles and then find the area of each triangle separately. At last, both the area of triangles are added to find the final area of the quadrilateral.
Area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD
Area of a triangle with vertices P(x1, y1), Q(x2, y2), and R(x3, y3) is given by
Area of Quadrilateral Using Bretschneider′s Formula
When two opposite angles and all the sides of a quadrilateral are given, we can calculate its area using Bretschneider’s Formula which is the extension of heron’s formula for quadrilaterals and is given as follows:
How to find the Area of a Quadrilateral?
Area of a quadrilateral is found by using the steps discussed below:
Step 1: Mark the length of the diagonal and the length of the perpendicular to it from both vertices.
Step 2: Put these values in the given formula Area = (1/2) × d ×( h1+h2 ), where d is the length of the diagonal and h1, h2 are lengths of the perpendicular from diagonal to opposite vertices.
Step 3: Answer obtained from the above step is the required area and is measured in unit2
Area of Some Quadrilaterals
Some specific quadrilaterals are very common and are used in our daily life and their formula for areas are explained in the article given below:
Area of a Square
A square is a special case of a rectangle in which the four sides are equal and all the sides are parallel to each other. In a square diagonal bisect perpendicularly to each other.
Read More on Area of Square
Area of a Rectangle
A rectangle is a closed figure having four sides in which opposite sides are equal and parallel to each other and the diagonals of the rectangles bisect at 90 degrees.
Read More on Area of Rectangle
Area of Rhombus
A Rhombus is a special case of the square in which all the four sides and opposite angles are the same in measure and the opposite sides are parallel and the sum of the adjacent angles of a rhombus is equal to 180 degrees.
Where D1 and D2 are the length of diagonals of Rhombus.
Read More on Area of Rhombus
Area of Parallelogram
The quadrilateral in which opposite sides are equal and parallel to each other is known as a parallelogram. In this, diagonals bisect each other and the opposite angles are of equal measure in which the sum of two adjacent angles of a parallelogram is equal to 180 degrees.
Read More on Area of Parallelogram
Area of Trapezium
This quadrilateral is somewhat different from the others as there is only one pair of the opposite side of a trapezium parallel to each other and the adjacent sides are supplementary to each other and the diagonals bisect each other in the same ratio.
Read More on Area of Trapezium
Area of Kite
Kite is a special quadrilateral in which each pair of consecutive sides is congruent, but the opposite sides are not congruent. In this, the largest diagonal of a kite bisects the smallest diagonal.
where, D1 = long diagonal of kite(CD), D2 = short diagonal of kite(AB)
Read More on Area of Kite
Solved Example on Area of Quadrilateral
Example 1: Find the area of the quadrilateral ABCD when its vertices are (1, 2), (5, 6), (4, −6), and (−5, 2).
Solution:
Let A(1, 2), B(5, 6), C(4, -6), and D(-5, 2) be the vertices of a quadrilateral ABCD.
A(1, 2) = (x1, y1), B(5, 6) = (x2, y2), C(4, -6) = (x3, y3), D(-5, 2) = (x4, y4)
We know that,
Area of Quadrilateral = (1/2) × [(x1y2 + x2y3 + x3y4 + x4y1) – (x2y1 + x3y2 + x4y3 + x1y4)]
⇒ Area of Quadrilateral = (½). {[1(6) + 5(-6) + 4(2) + (-5)2] – {[5(2) + 4(6) + (-5)(-6) + 1(2)]}
⇒ Area of Quadrilateral = (½).[(6 – 30 + 8 – 10) – (10 + 24 + 30 + 2)]
⇒ Area of Quadrilateral = (½) [-26 – 66]
⇒ Area of Quadrilateral = 92/2 (area is never negative)
⇒ Area of Quadrilateral = 46 unit2
Example 2: Find the area of the trapezium if height is 5 cm and AB and CD are given as 10 and 6 cm respectively.
Solution:
Given, AB = 10cm, CD = 6cm, height = 5cm
According to the formulae,
Area of Trapezium = (1/2) h (AB+CD)
⇒ Area of Trapezium = 1/2 x 5 x (10 + 6)
⇒ Area of Trapezium = 40 cm2
Example 3: Find the area of a kite whose longest and shortest diagonals are 20cm and 10cm respectively.
Solution:
Length of longest diagonal, D1= 20 cm
Length of shortest diagonal, D2= 10 cm
So, Area of kite =1/2 x D1 x D2
⇒ Area of kite = 1/2 x 20 x 10
⇒ Area of kite = 100 cm2
Example 4: Calculate the area of a parallelogram, if the base and height are 10 m and 15 m respectively.
Solution:
Given, base = 10 m and height = 15 m
Area of Parallelogram = Base x Height
⇒ Area of Parallelogram = 10 x 15
⇒ Area of Parallelogram = 150 m2
Example 5: Given the area of the rhombus is 120-meter square then find the length of one of the diagonals if the other diagonal is of length 12 m.
Solution:
Since we know that,
Area of Rhombus = (1/2) x Diagonal1 x Diagonal2
Putting all the known values, we get
120 = (1/2) x Diagonal 1 x Diagonal 2
Diagonal 2 = 20 m
FAQs on Area of Quadrilateral
Question 1: What is the area of a quadrilateral?
Answer:
Area of the quadrilateral is the region inside the boundary of a quadrilateral. It is the total space occupied by a quadrilateral in 2-D plane. It is measured in square units.
Question 2: How to find the area of a quadrilateral?
Answer:
Area of quadrilateral is found using formula given below:
Area of Quadrilateral = (1/2) × [(x1y2 + x2y3 + x3y4 + x4y1) – (x2y1 + x3y2 + x4y3 + x1y4)]
where (x1, y1), (x2, y2), (x3, y3), and (x4, y4) are the vertices of a quadrilateral.
Question 3: What are the different types of quadrilaterals?
Answer:
Different types of quadrilateral are:
- Square
- Rectangle
- Rhombus
- Kite
- Parallelogram
- Trapezium
Question 4: Write the uses of quadrilaterals.
Answer:
Area of quadrilateral is used in the field of architecture, agriculture, design, and navigation also it helps to find distance between two points. It is required to find the area of buildings, park and other complexes.
Question 5: How to calculate the area of a quadrilateral if one of its diagonals and both perpendiculars from the vertices are given?
Answer:
When the diagonal(d) and the length of both perpendiculars (h, H) from the vertices are given, then the area of the quadrilateral is calculated by the formula:
Area of quadrilateral = (½) × d × (h + H)
Question 6: What are the two main types of quadrilaterals?
Answer:
The two main types of a quadrilateral are
- Regular Quadrilateral
- Irregular Quadrilateral
Question 7: How to find the Area of a Quadrilateral using Heron’s Formula?
Answer:
To find area of triangle using Heron’s Formula use the following steps:
Step 1: Divide the quadrilateral in two triangles by joining its diagonal.
Step 2: Find the area of both triangles using Heron’s formula.
Step 3: Add both the areas to get the final answer.
§3. Площади четырёхугольников
В школьном учебнике выведены следующие формулы площади параллелограмма:
`S=a*h_a=b*h_b`, (6)
`S=a*bsinvarphi` (7)
Где `a` и `b` — стороны параллелограмма, `h_a` и `h_b` — высоты к ним, `varphi` — величина угла между сторонами параллелограмма.
Докажем теорему о площади четырёхугольника.
Площадь выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними, т. е
`S=1/2d_1d_2sinalpha` (8)
где `d_1` и `d_2` — диагонали четырёхугольника, `alpha` — величина угла между ними.
`ABCD` — выпуклый четырёхугольник, диагонали которого `AC` и `BD` пересекаются в точке `O` под углом `alpha` (рис. 15). Через вершины `A` и `C` проведём прямые, параллельные диагонали `BD`, а через вершины `B` и `D` проведём прямые, параллельные диагонали `AC`. Проведённые прямые в пересечении образуют параллелограмм со сторонами, равными диагоналям `BD` и `AC`, и углом `alpha`. Площадь параллелограмма равна `AC*BD*sinalpha`, а площадь четырёхугольника `ABCD` равна, как легко видеть, половине его площади, т. е.
`S_(ABCD)=1/2AC*BD*sinalpha`.
Площадь ромба равна половине произведения его диагоналей. Это сразу следует из доказанной формулы, т. к. диагонали ромба перпендикулярны.
Найти площадь параллелограмма, стороны которого равны `a` и `b` `(a!=b)`, а угол между диагоналями равен `alpha(alpha<90^@)`.
Пусть `O` — точка пересечения диагоналей параллелограмма `ABCD` (рис. 16), `AB=a`, `AD=b`. Обозначим `BD=2x`, `AC=2y`.
Применим теорему косинусов к треугольникам`AOB` и `AOD` (заметим, что `/_AOD=180^@-alpha)`, будем иметь: `a^2=x^2+y^2-2xycosalpha`, `b^2=x^2+y^2+2xycosalpha`. По теореме 3 площадь `S` параллелограмма `ABCD` будет равна `1/2AC*BDsinalpha=2xysinalpha`. Заметим, что это выражение легко можно найти, не определяя `x` и `y` из системы. Действительно, из двух уравнений для `x` и `y` получим `b^2-a^2=4xycosalpha`. По условию `b!=a`, следовательно, `cosa!=0` и `xy=(b^2-a^2)/(4cosalpha)`. Выражаем площадь параллелограмма по формуле (8):
`S=2xysinalpha=(b^2-a^2)/2 «tg»alpha`.
Середины сторон выпуклого четырёхугольника `ABCD` являются вершинами другого четырёхугольника (четырёхугольника Вариньона). Доказать, что четырёхугольник Вариньона — параллелограмм и его площадь равна половине площади `S` четырёхугольника `ABCD`.
1. Проведём диагонали `AC` и `BD`. Середины сторон обозначим `K`, `L`, `M` и `N` (рис. 17). По определению `KL` — средняя линия треугольника `ABC`, по теореме о средней линии `KL«||«AC`, `KL=1/2AC`.
Аналогично, `NM` — средняя линия треугольника `ADC`, `NM«||«AC`, `NM=1/2AC`.
В четырёхугольнике `KLMN` противоположные стороны `KL` и `NM` равны и параллельны, по признаку `KLMN` — параллелограмм.
Если рассмотреть стороны `LM` и `KN`, то точно также установим, что `LM«||«BD«||«KN` и `LM=KN=1/2BD`.
2. Из параллельности `KL«||«AC` и `KN«||«BD` следует, что угол `LKN` параллелограмма `KLMN` равен углу между диагоналями четырёхугольника `ABCD` (обозначим угол `alpha`).
Имеем `S_(KLMN)=KL*KNsinalpha=1/2AC*1/2BDsinalpha`, а по теореме 3
`S_(ABCD)=1/2AC*BD*sinalpha`.
Из этого следует `S_(KLMN)=1/2S_(ABCD)`, ч. т. д.
Рассмотрим несколько задач, где определяется или используется площадь трапеции. Напомним,
что площадь трапеции равна произведению полусуммы оснований на её высоту, т. е.
`S=(a+b)/2h`. (9)
Найти площадь трапеции, если её основания равны `16` и `44`, а боковые стороны равны `17` и `25`.
Через вершину `C` проведём `CK«||«BA` (рис. 18). `ABCK` — параллелограмм, его противоположные стороны равны, поэтому в треугольнике `KCD` определяются все стороны: `KC=AB=25`, `CD=17`, `KD=AD-BC=28`.
По формуле Герона вычисляем площадь этого треугольника: `p=36`, `S_(KCD)=210`.
С другой стороны, `S_(KCD)=1/2KD*CF`, если `CF_|_AD`. Отсюда находим `CF=(2S_(KCD))/(KD)=15` и вычисляем площадь трапеции
`S_(ABCD)=1/2(BC+AD)CF=450`.
Отрезок длины `m`, параллельный основаниям трапеции, разбивает её на две трапеции (рис. 19). Найти отношение площадей этих трапеций, если основания трапеции равны `a` и `b` `(b < a)`.
Пусть `BC=b`, `AD=a` и `MN=m`, и `MN«||«AD`. Проведём `CE«||«BA` и `NF«||«BA`, а также `CK_|_MN` и `NP_|_AD`. Обозначим `CK=h_1`, `NP=h_2`. Далее, т. к. `CE«||«NF`, то `/_ECN=/_FND`, а из `MN«||«AD` следует `/_ENC=/_FDN`. Следовательно, треугольники `ECN` и `FND` имеют по два равных угла, они подобны. Из подобия имеем `(EN)/(FD)=(CN)/(ND)`. Прямоугольные треугольники `KCN` и `PND` также подобны и `(CK)/(NP)=(CN)/(ND)`, поэтому `(EN)/(FD)=(CK)/(NP)`, т. е. `(m-b)/(a-m)=(h_1)/(h_2)`. Если `S_1` и `S_2` — площади трапеций `MBCN` и `AMND`, то
`S_1=1/2(b+m)h_1`, `S_2=1/2(a+m)h_2`
и
`(S_1)/(S_2)=((m+b)h_1)/((a+m)h_2)=(m^2-b^2)/(a^2-m^2`.













































