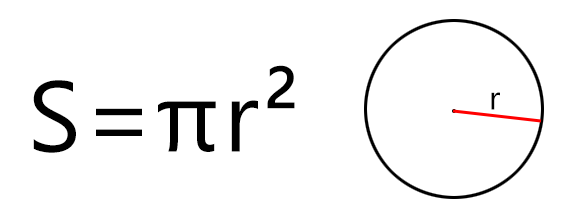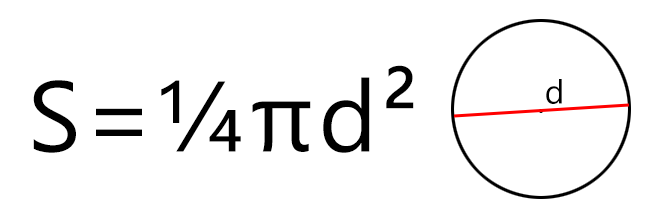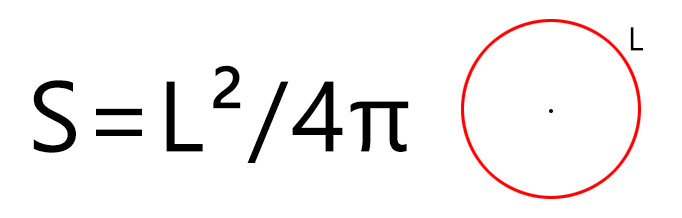Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
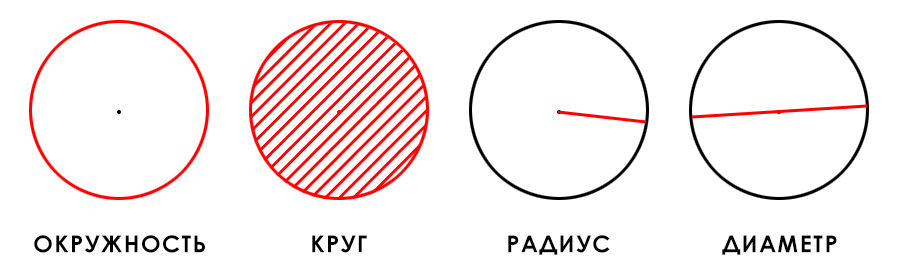
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Через радиус
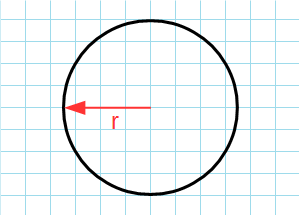
Формула для нахождения площади круга через радиус:
π — константа равная (3.14); r — радиус круга.
Через диаметр
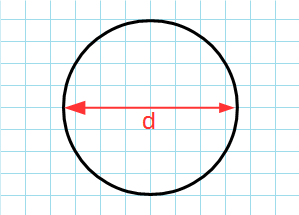
Формула для нахождения площади круга через диаметр:
π — константа равная (3.14); d — диаметр.
Через длину окружности

Формула для нахождения площади круга через длину окружности:
π — константа равная (3.14); l — длина окружности.
Площадь круга. Онлайн-калькулятор
Онлайн калькулятор для расчета площади круга. Рассчитать площадь круга можно двумя способами: через радиус и диаметр круга. После выбора вариант расчета, задайте радиус или диаметр и нажмите кнопку «Рассчитать». Наш калькулятор выведет результат расчета площади, а также покажет подробное решение, с помощью которого можно посмотреть как был получен результат.

Выберите способ расчета площади:
Рассчитать
Круг – это плоскость, которая ограничена окружностью.
Как найти площадь круга?
Площадь круга рассчитывается двумя способами:
1) через радиус круга
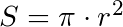
r – радиус круга.
2) через диаметр круга

d – диаметр круга.
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас
слышал про эту знаменитую спортивную игру. Всем известно,
что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть
людей скажут, что форму шара, а часть, что формы сферы. Так кто же
из них прав? И в чем разница между сферой и шаром?
Важно!
Шар — это пространственное тело. Внутри шар
чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
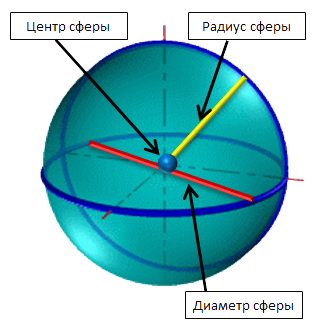
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
Важно!
Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.
Как найти площадь сферы
Запомните!
Формула площади сферы:
S = 4πR2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π R2 =
4πR · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
-
Вычислите площадь сферы, если её радиус равен
1 м. (возьмите π как
3)
Вспомнив, как выделить целую часть
и перемножить дроби,
воспользуемся формулой площади сферы:
S = 4 · πR2 =
4 · 3 ·
(1 ) 2 =
4 · ·
() 2 =
4 · ·
=
=
= =
=
=
45
м2
Как найти объем шара
Запомните!
- Формула объема шара:
V = πR3
Зная определение степени,
можно записать формулу объема шара следующим образом.
-
V =
π R3 =π R · R · R;
Для отработки полученных знаний решим задачу на объем шара.
Зубарева 6 класс. Номер 691(а)
Условие задачи:
-
Вычислите радиус шара, если его объем равен
4 м3 (возьмите π как
3)
Выразим из формулы объема шара радиус.
- V =
π R3 -
π R3
= V -
π R3
=
-
R3
=
Подставим в формулу известные нам значения. Число π
возьмем как задано в задании «3».
R3
= (3 ·
4) /
(4 · 3)
Чтобы не запутаться, отдельно рассчитаем
числитель дроби.
3 ·
4 =
3 ·
=
=
Теперь снова подставим полученное значение в нашу формулу:
-
R3
=
/ (4 · 3)=
/ (4 · )
=
/ () =
=
· () =
= =
=
= 1
- R3 = 1
- R = 1 м
Важно!
Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 февраля 2019 в 22:59
Руслан Магомедов
Профиль
Благодарили: 0
Сообщений: 1
Руслан Магомедов
Профиль
Благодарили: 0
Сообщений: 1
Рассчитайте объем чашки высотой 7 см с диаметром 6,5 с
0
Спасибо
Ответить
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d — диаметр, а π – константа, равная 3,1415…):
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L — длина окружности, а π – константа, равная 3,1415…):
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
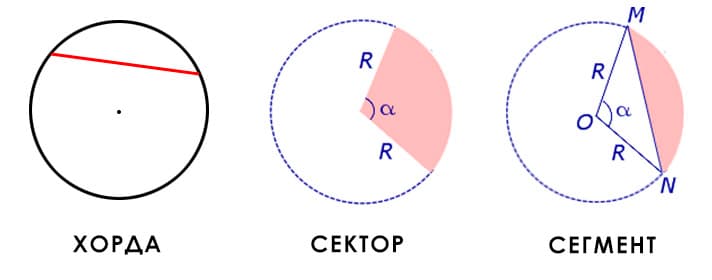
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Найти площадь круга поможет калькулятор онлайн, который быстро и точно вычислит искомую величину. Площадь круга можно считать через диаметр или радиус. Здесь есть 2 калькулятора которыми мы рассчитываем площадь круга через диаметр и через радиус.
Калькулятор площади круга через диаметр
Калькулятор площади круга через радиус
Расчет площади круга на калькуляторе онлайн
Расчет площади круга пожалуй самый популярный вопрос в сети. Этот расчет может пригодиться практически любому человеку, начиная от школьника и заканчивая инженером. Поэтому мы тоже решили обязательно добавить на наш сайт точный калькулятор площади круга. Просто введите диаметр или радиус круга, нажмите на кнопку «Рассчитать» и мгновенно получите результат. Даже нажимать на неё не обязательно, всё на автомате. Результаты выводятся в нужных вам единицах измерения.
Площадь круга в основном считается двумя способами, а именно:
- площадь круга через диаметр
- площадь круга через радиус
Каким именно способом пользоваться решать вам. Он зависит от конкретной задачи и имеющихся исходных данных (размеров).
Наш онлайн-калькулятор площади круга удобен тем, что можно выбрать различные единицы измерения диаметра круга и рассчитанной площади круга. Стоит только переключиться и всё будет тут же пересчитано. К тому же у него очень хорошая точность, в чём вы можете легко убедиться сами.
И еще, имейте ввиду, что калькулятор округляет результат до 3-х знаков после запятой. Для обычных расчётов этого вполне достаточно. Если понадобится еще большая точность, напишите об этим в комментариях.
Формула площади круга через диаметр
S = π * D2 / 4 , где
S — площадь круга,
D — диаметр круга,
π — число «Пи».
Формула площади круга через радиус
S = π * R2 , где
S — площадь круга,
R — радиус круга,
π — математическая константа.
Как видите формулы для расчёта площадей круга очень простые, однако лучше всего площадь круга вычислит онлайн калькулятор. В таком случае будет меньше ошибок и не будет путаницы в единицах измерения.
Таблица площади круга в зависимости от диаметра
| Диаметр круга, см | Площадь круга, см2 |
|---|---|
| 1 | 0,79 |
| 2 | 3,14 |
| 3 | 7,07 |
| 4 | 12,57 |
| 5 | 19,64 |
| 10 | 78,54 |
| 15 | 176,72 |
| 20 | 314,16 |
| 25 | 480,87 |
| 50 | 1963,50 |
| 100 | 7853,98 |
| 200 | 31415,93 |
Пригодилось? Добавьте в закладки чтобы не потерять или нажмите на «поделиться».
Было полезно? Поделитесь с друзьями!