Всего: 99 1–20 | 21–40 | 41–60 | 61–80 | 81–99
Добавить в вариант
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 7,5. Найдите объем исходной призмы.
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 48 и высота равна 7.
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 40 и высота равна 15.
Площадь боковой поверхности цилиндра равна а высота — 1. Найдите диаметр основания.
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 3 и 9, а второго — 6 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Стороны основания правильной шестиугольной пирамиды равны 14, боковые рёбра равны 25. Найдите площадь боковой поверхности этой пирамиды.
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6, а боковое ребро равно
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 5, а второго — 5 и 6. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 5, а второго — 5 и 6. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 4 и 6, а второго — 2 и 8. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 7 и 9, а второго — 2 и 9. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 5 и 6, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?
Сторона основания правильной четырехугольной пирамиды равна 4, а боковое ребро равно Найдите объем пирамиды.
Основания трапеции равны 16 и 22, боковая сторона, равная 10, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
Сторона основания правильной четырехугольной пирамиды равна 6, а боковое ребро равно Найдите объем пирамиды.
В правильной треугольной призме ABCA1B1C1 стороны оснований равны боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, и A1B1 и точку С.
Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
Площадь боковой поверхности конуса в
раз больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 43. Найдите площадь боковой поверхности исходной призмы.
Источник: ЕГЭ по математике — 2015. Досрочная волна, вариант ФИПИ
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно
Источники:
Демонстрационная версия ЕГЭ — 2018;
Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Всего: 99 1–20 | 21–40 | 41–60 | 61–80 | 81–99
Формулы объёма и площади поверхности. Многогранники.
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
 Куб |
|
|
 Параллелепипед |
|
|
 Прямоугольный параллелепипед |
|
|
 Призма |
|

|
 Пирамида |
|

|
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат),
(маленький прямоугольник),
Подставим все данные в формулу: 
Ответ: 424.
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник),
(маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно,
большая боковая грань призмы.
Поэтому или
откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
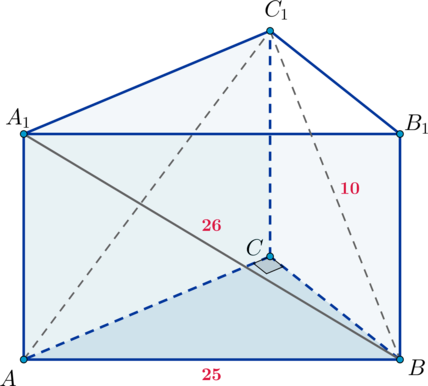
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда
(по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда
следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как
высота воды
должна быть в 81 раз меньше, чем
Она равна
(см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту
Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, 
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
|
Источник: Решу ЕГЭ Задача на обыкновенную формулу Герона, которая позволяет вычислить площадь треугольника по длинам всех его сторон. Боковая поверхность данной пирамиды — это 6 равнобедренных треугольников с основанием 16 и сторонами 17 каждый. Полупериметр каждого такого треугольника — (16 + 17 + 17) / 2 = 25 25 — 16 = 9 25 — 17 = 8 Площадь такого треугольника — это (25 * 8 * 8 * 9)^1/2 = 5 * 3 * 8 = 120, площадь всех шести треугольников равна, соответственно, 120 * 6 = 720, это и будет ответом. Конечно, есть и более простая формула для расчета площади именно равнобедренного треугольника по его основанию и боковой стороне. Однако она будет все той же переделанной формулой Герона для частного случая. Знаете ответ? |
Тема 13.
Задачи по стереометрии
13
.
17
Нахождение объема или площади поверхности
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи по стереометрии
Решаем задачи
Показать ответ и решение
а) Так как
то по теореме о трех перпендикулярах
Следовательно,
—
прямоугольный.
б) Заметим, что и
следовательно, по признаку перпендикулярности прямой и плоскости
Следовательно, — высота пирамиды
с основанием
Так как — прямоугольный, то
По теореме Пифагора имеем:
Тогда искомый объем равен
Ответ:
б)
Критерии оценки
|
Содержание критерия |
Балл |
|
Имеется верное доказательство |
3 |
|
Обоснованно получен верный ответ в |
2 |
|
ИЛИ |
|
|
имеется верное |
|
|
Имеется верное доказательство |
1 |
|
ИЛИ |
|
|
при обоснованном решении пункта |
|
|
ИЛИ |
|
|
обоснованно получен верный ответ в |
|
|
Решение не соответствует ни одному |
0 |
|
Максимальный балл |
3 |
Показать ответ и решение
а) Рассмотрим прямоугольник в плоскости
В нём
— это средняя линия, значит,
Отсюда так как
по условию.
В плоскости грани проведём через точку
прямую, перпендикулярную
Пусть она пересекает сторону
в точке
то есть
Заметим, что
как диагонали квадрата, следовательно,
Рассмотрим треугольники и
Они подобны, так как
значит,
В кубе ребро
перпендикулярно грани
значит,
Через точки
и
в
плоскостях и
соответственно проведем прямые
и
параллельные
Точки
и
лежат на и
соответственно. Тогда
Плоскость образована прямыми
и
, которые перпендикулярны прямой
значит,
Тогда — это плоскость
Точка
значит, искомое отношение равно
б) Рассмотрим многогранник отсечённый от куба плоскостью
Он является прямой призмой с
основанием и высотой
так как треугольник
лежит в плоскости
а
и
Пусть длина каждого ребра куба равна Тогда, так как
то отрезки
Поскольку прямоугольный, то имеем:
Объём всего куба равен тогда имеем:
Ответ:
б)
Критерии оценки
|
Содержание критерия |
Балл |
|
Имеется верное доказательство |
3 |
|
Обоснованно получен верный ответ в |
2 |
|
ИЛИ |
|
|
имеется верное |
|
|
Имеется верное доказательство |
1 |
|
ИЛИ |
|
|
при обоснованном решении пункта |
|
|
ИЛИ |
|
|
обоснованно получен верный ответ в |
|
|
Решение не соответствует ни одному |
0 |
|
Максимальный балл |
3 |
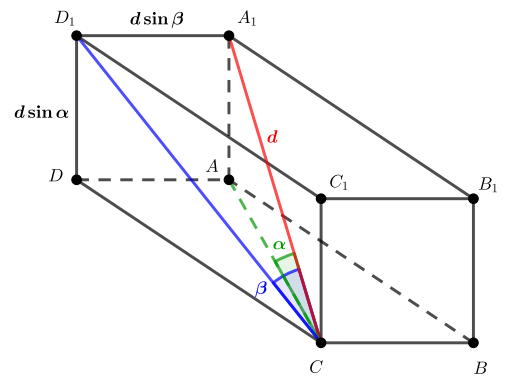
Показать ответ и решение
Будем считать, что — длина диагонали
,
— это угол между диагональю и гранью
, а
— угол
между диагональю и гранью .
Известно, что угол между прямой и плоскостью равен углу между прямой и ее проекцией на эту плоскость. Также
мы знаем, что проекциями диагонали на грани в прямоугольном параллелепипеде являются соответствующие
диагонали граней. Из этого получаем, что .
— прямоугольный с прямым углом
,
— прямоугольный с прямым углом
, кроме того,
— прямоугольник и
, тогда
По теореме Пифагора для треугольника
Итого, объем параллелепипеда равен
Ответ:
Показать ответ и решение
а) Пусть – высота пирамиды,
– точка пересечения медиан. Следовательно,
Так
как по условию , то можно обозначить
,
. Тогда
.
Следовательно, ,
,
.
Так как перпендикулярна плоскости
, то нужно построить две пересекающиеся прямые в
плоскости , которым
будет перпендикулярна.
Первая прямая: так как , то проведем через точку
прямую
. Тогда
().
Вторая прямая: так как , то
. Следовательно, проведем
, тогда
(
).
Следовательно, проходит через точки
.
Заметим, что пересечет плоскость
по прямой, параллельной
(в противном случае
будет иметь общую точку с , что невозможно, так как
).
Следовательно, и проходит через
.
Из подобия :
Из
подобия :
б) Рассмотрим пирамиду .
– высота этой пирамиды,
– трапеция
().
Следовательно,
Так
как , то
. Следовательно,
Из
подобия :
Из
пункта а)
Из
подобия :
Следовательно,
Показать ответ и решение
1) 
Пусть – высота пирамиды, то есть
– точка пересечения биссектрис основания. Рассмотрим
основание . Так как центр вписанной в треугольник окружности лежит на пересечении
биссектрис, то – центр вписанной окружности. Пусть
– биссектрисы, тогда
также
медиана и высота, так как . Следовательно,
, следовательно,
и есть
радиус вписанной окружности.
Проведем . Тогда
. Пусть
. Тогда
.
Тогда из подобия :
Следовательно, . Тогда
.
Значит, площадь основания
2) 
Заметим, что прямоугольный, следовательно, для того, чтобы найти высоту пирамиды,
нужно найти . Из прямоугольного
:
Следовательно,
Следовательно, объем пирамиды равен
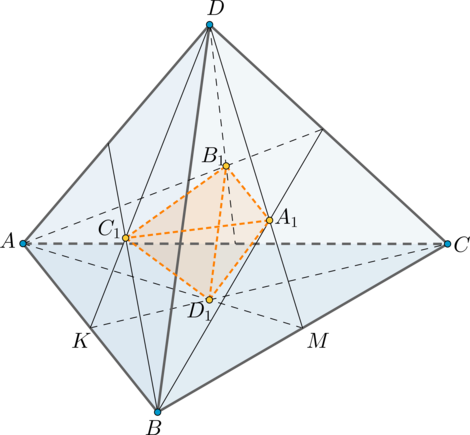
Площадь полной поверхности тетраэдра равна . Найдите площадь полной поверхности
пирамиды, вершинами которой являются точки пересечения медиан граней данного тетраэдра.
Показать ответ и решение
Пусть – тетраэдр, точки
— точки пересечения медиан в гранях
соответственно.
1) Т.к. медианы точкой пересечения делятся в отношении , считая от вершины, то
. Следовательно,
по углу и двум прилежащим
пропорциональным сторонам. Таким образом, (
как соответственные)
и .
Аналогичным образом можно доказать, что ,
.
2) с коэффициентом
, то есть
. А вот
с
коэффициентом (т.к.
– средняя линия), то есть
.
Следовательно, .
Аналогично доказывается, что ,
.
3) Таким образом, все ребра тетраэдра в три раза меньше соответствующих ребер
тетраэдра , а это значит, что каждая грань тетраэдра
подобна с коэффициентом
соответствующей грани тетраэдра .
4) Т.к. площади подобных треугольников относятся как квадрат коэффициента подобия, то площадь
каждой грани тетраэдра равна
от площади соответствующей грани тетраэдра
.
Следовательно,
Показать ответ и решение
Способ 1.
1) Рассмотрим правильную пирамиду ,
– высота (которая падает в точку
пересечения диагоналей основания), .
Напомним, что у правильной пирамиды все боковые грани представляют собой равные равнобедренные
треугольники.
Введем вспомогательный угол между боковым ребром и основанием: .
Тогда , следовательно,
.
Тогда, т.к. площадь треугольника равна полупроизведению сторон на синус угла между
ними,
2) Теперь необходимо выразить через данные в условии величины.
Проведем – медиану и высоту в равнобедренном
. Тогда
как диагональ квадрата, следовательно,
. В
:
Разделим равенство на равенство
и получим:
Тогда .
3) Таким образом,
4) Подставляя значения из условия, находим, что
Способ 2.
Пусть длина квадрата основания равна . Тогда
а
Выразим
квадраты длин и
по теореме Пифагора для треугольника
Запишем теорему косинусов для , выразив квадрат стороны
Подставим полученное выражение для в формулу
.
Выразим площадь треугольника
Тогда
Ответ:
В основании треугольной пирамиды лежит равносторонний треугольник
.
Все боковые грани наклонены к плоскости основания под углом . Пирамида не является
правильной.
а) Докажите, что высота пирамиды падает в центр вневписанной для треугольника
окружности.
б) Найдите объем пирамиды, если , а сторона основания равна
.
Показать ответ и решение
Таким образом, . Таким образом, тока
равноудалена от прямых
. Значит, это либо центр вписанной в
окружности, либо центр вневписанной
окружности (касающейся стороны и продолжений двух других сторон). Т.к. пирамида не является
правильной, то первый вариант не подходит, чтд.
б) Обозначим . Пусть для определенности
– центр окружности, касающейся
стороны и продолжений сторон
и
. Тогда
лежит на биссектрисе угла
.
Следовательно, – биссектриса, а т.к.
– правильный, то
. Следовательно, точка
лежит на биссектрисе
.
Значит, . Т.к. отрезки касательных, проведенных из одной точки, равны, то
. Следовательно,
. К тому же
(как половина
).
Значит,
Следовательно, . Из прямоугольного
Таким образом, объем пирамиды равен
Ответ:
б)
Показать ответ и решение
а) Рассмотрим пирамиду В ней по условию
Так как и
— равнобедренные, причем
— общее основание, то высоты к основаниями попадут в одну точку
— в середину стороны
Тогда
Таким образом,
— линейный угол двугранного угла
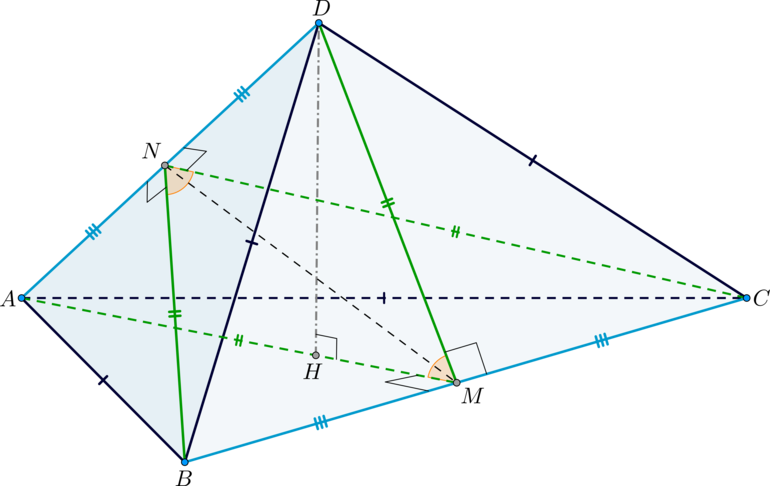
Аналогичным образом строится угол — линейный угол двугранного угла
где
— середина
Таким образом,
Так как по трем сторонам, то
Аналогично
Значит,
и
—
равнобедренные и подобные по двум пропорциональным сторонам и углу между ними.
Заметим, что плоскости и
имеют две общие точки — это точки
и
. Следовательно, они пересекаются по
прямой Отрезок
— это высота в
и
к основаниям
и
соответственно. Следовательно, эти
треугольники равны. Следовательно, Что и требовалось доказать.
б) 
Из пункта а) также следует, что
Так как двугранные углы равны то
и
— равносторонние.
Пусть
Проведем высоту пирамиды Так как
то по теореме о трех перпендикулярах
Таким образом,
точка должна лежать на
причем на середине, так как
— равносторонний. Тогда
Найдем по теореме Пифагора из
Таким образом,
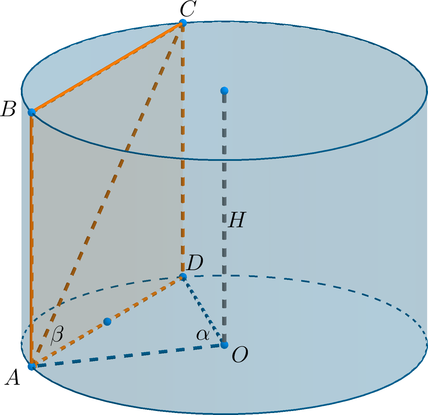
Параллельно оси цилиндра проведена плоскость, отсекающая от окружности основания дугу, градусная мера которой равна
Диагональ сечения наклонена под углом к основанию цилиндра.
а) Найдите объем цилиндра, если высота цилиндра равна
б) Вычислите объем цилиндра, если
Показать ответ и решение
а) Сечение цилиндра данной плоскостью — это прямоугольник где
Дуга
следовательно,
центральный угол
Объем цилиндра равен
Здесь следовательно, необходимо найти
Рассмотрим прямоугольный треугольник В нем имеем:
Заметим, что — равнобедренный. Тогда по теореме косинусов
Тогда имеем:
Следовательно, объем цилиндра равен
б) Подставляя значения из условия, получаем:
Критерии оценки
|
Содержание критерия |
Балл |
|
Имеется верное доказательство |
3 |
|
Обоснованно получен верный ответ в |
2 |
|
ИЛИ |
|
|
имеется верное |
|
|
Имеется верное доказательство |
1 |
|
ИЛИ |
|
|
при обоснованном решении пункта |
|
|
ИЛИ |
|
|
обоснованно получен верный ответ в |
|
|
Решение не соответствует ни одному |
0 |
|
Максимальный балл |
3 |
Образующая усеченного конуса составляет с плоскостью нижнего основания угол . Диагональ его
осевого сечения перпендикулярна образующей конуса. Сумма длин окружностей оснований равна
.
а) Найдите площадь боковой поверхности усеченного конуса.
б) Вычислите эту площадь, если ,
.
Показать ответ и решение
а)
Обозначим за и
– радиусы нижнего и верхнего оснований усеченного конуса соответственно.
Тогда из условия сумма длин окружностей оснований равна
2) Для того, чтобы найти площадь боковой поверхности усеченного конуса, нужно из
площади боковой поверхности всего конуса вычесть площадь боковой поверхности маленького
конуса:
Заметим, что и
– прямоугольные, следовательно,
Значит, площадь боковой поверхности уже приобретает вид:
Необходимо найти .
3) Т.к. , то
– прямоугольный, следовательно,
Из данных второго пункта мы можем сказать, что
Таким образом, имеем:
Но , следовательно,
, следовательно,
Подставляя это значение для в
, находим, что
Таким образом,
4) Значит, площадь боковой поверхности равна
б) Подставляя значения из условия и помня, что , найдем площадь боковой
поверхности:
Ответ:
а)
б)
Показать ответ и решение
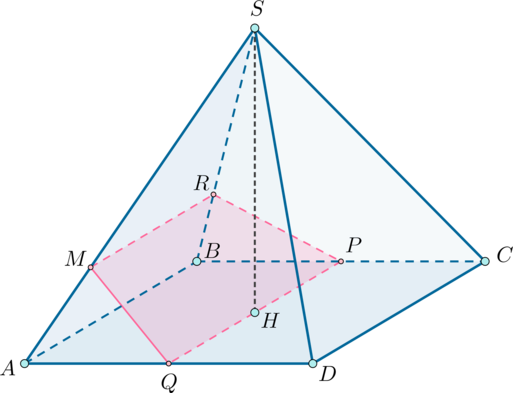
а) Пусть – высота пирамиды, следовательно, так как пирамида правильная,
– точка
пересечения диагоналей квадрата . Тогда отрезок
пройдет через точку
, причем
. Построим сечение пирамиды плоскостью
.
Плоскости и
пересекаются по прямой
, плоскости
и
— по
прямой . Так как
, то плоскости
и
пересекутся по прямой
.
Действительно, если это не так, то есть , то
– это общая точка плоскости
и плоскости
, следовательно,
. Но
, следовательно,
,
что невозможно, так как .
Таким образом, – трапеция.
Так как , то по теореме Фалеса
. Так как пирамида правильная,
то ее боковые ребра равны, следовательно, . Также
и все боковые грани
представляют собой равные равнобедренные треугольники, то есть, например, .
Следовательно, , откуда
.
Значит, – равнобедренная трапеция.
б) Нужно найти отношение . Пусть
,
.
То есть нужно найти .
Введем обозначения: . Тогда
.
Найдем . Тогда
.
В пирамиде
– вершина,
– основание. Для того, чтобы найти ее объем, нужно
найти высоту .
Пусть – середина
. Так как
– середина
и трапеция
равнобедренная, то
, то есть
– высота трапеции.
Утверждение: точка лежит на прямой
.
Действительно, пусть проведена . Тогда, так как
(наклонная), то по
теореме о трех перпендикулярах (проекция). Так как к одной прямой в плоскости
не может быть проведено два различных перпендикуляра и
, следовательно,
.
Прямая пересечет
в точке
– середине
(так как
– середина
и
).
.
с коэффициентом
, следовательно,
.
Рассмотрим плоскость и трапецию
:
Из :
. Так как
,
, то
, следовательно,
Тогда по теореме косинусов из (
):
Заметим, что
По
теореме синусов их :
Тогда из прямоугольного :
Таким образом,
Тогда
Также
Следовательно,
Ответ:
б)
Показать ответ и решение
Если – точка пересечения прямых
и
, то
. Так как также
(так как трапеция равнобедренная), то равносторонний и
. Следовательно, и
.
Пусть – центр основания конуса,
– вершина. Тогда
.
Заметим, что если в плоскости провести
, то
(так как
и
). Следовательно, прямые
и
параллельны, следовательно, лежат в одной
плоскости, причем это плоскость (так как
).
Рассмотрим грань . Пусть
– радиус вписанной окружности. Тогда
по
свойству прямоугольного треугольника., следовательно,
можно найти из прямоугольного :
лежит против угла
, значит,
. Также по теореме Пифагора можно найти
.
Следовательно,
Рассмотрим : он подобен
, значит,
Следовательно, .
Тогда объем конуса равен:
Ответ:
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение объемов и площадей
Напомним объемы некоторых пространственных фигур:
(blacktriangleright) Объем пирамиды ({large{V=dfrac{1}{3}S_{text{осн}}h}}) , где (S_{text{осн}}) – площадь основания, (h) – высота.
(blacktriangleright) Объем призмы ({large{V=S_{text{осн}}cdot
h}}), где (S_{text{осн}}) – площадь основания, (h) – высота.
Т.к. параллелепипед — частный случай призмы, то его объем ищется по той же формуле.
(blacktriangleright) Объем прямоугольного параллелепипеда ({large{V=abc}}), где (a, b, c) – три различных боковых ребра.
(blacktriangleright) Объем куба ({large{V=a^3}}), где (a) – ребро куба.
(blacktriangleright) Объем конуса ({large{V=dfrac{1}{3}pi
r^2h}}), где (r) – радиус основания, (h) – высота конуса.
(blacktriangleright) Объем цилиндра ({large{V=pi r^2h}}), где (r) – радиус основания, (h) – высота цилиндра.
(blacktriangleright) Объем шара ({large{V=dfrac{4}{3}pi R^3}}), где (R) — радиус шара.
Задание
1
#2885
Уровень задания: Легче ЕГЭ
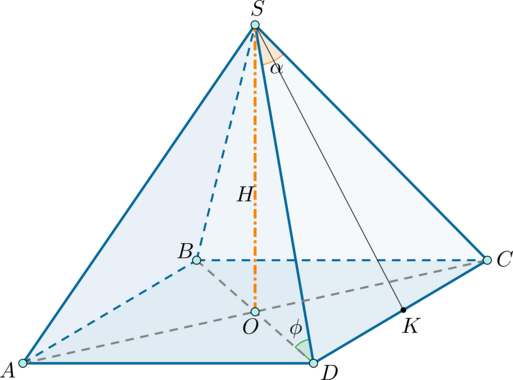
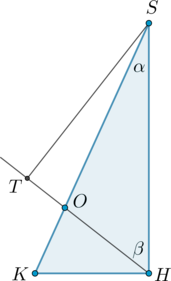
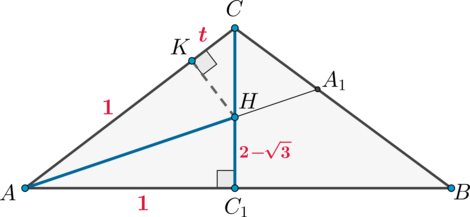
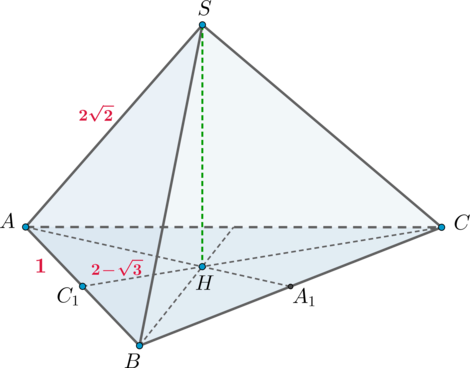
Дана пирамида (SABC) с вершиной (S), высота которой падает в точку пересечения биссектрис основания, являющегося равнобедренным треугольником с (AC=CB). Известно, что радиус вписанной в треугольник (ABC) окружности равен (2-sqrt3), (AB=2), (AS=2sqrt2). Найдите объем пирамиды.
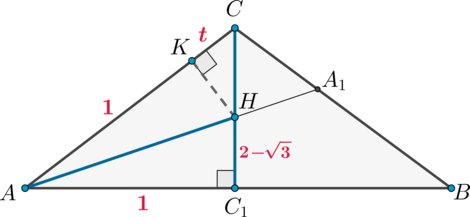
1)
Пусть (SH) – высота пирамиды, то есть (H) – точка пересечения биссектрис основания. Рассмотрим основание (ABC). Так как центр вписанной в треугольник окружности лежит на пересечении биссектрис, то (H) – центр вписанной окружности. Пусть (AA_1, CC_1) – биссектрисы, тогда (CC_1) также медиана и высота, так как (AC=CB). Следовательно, (HC_1perp AB), следовательно, (HC_1=r) и есть радиус вписанной окружности.
Проведем (HK=rperp AC). Тогда (AK=AC_1=1). Пусть (CK=t). Тогда (CC_1=sqrt{AC^2-AC_1^2}=sqrt{t(t+2)}). Тогда из подобия (triangle
KCHsim triangle ACC_1): [dfrac{HK}{AC_1}=dfrac{CK}{CC_1} quadRightarrowquad
dfrac{2-sqrt3}1=dfrac t{sqrt{t(t+2)}} quadRightarrowquad
t=dfrac2{sqrt3}-1] Следовательно, (AC=t+1=dfrac2{sqrt3}). Тогда (CC_1=dfrac1{sqrt3}).
Значит, площадь основания [S_{ABC}=dfrac12cdot ABcdot CC_1=dfrac1{sqrt3}.]
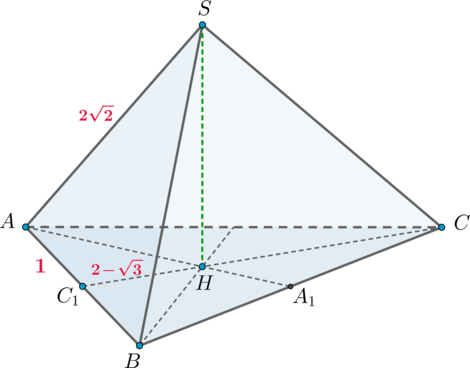
2)
Заметим, что (triangle ASH) прямоугольный, следовательно, для того, чтобы найти высоту пирамиды, нужно найти (AH). Из прямоугольного (AC_1H): [AH^2=AC_1^2+C_1H^2=1+(2-sqrt3)^2=4(2-sqrt3).] Следовательно, [SH=sqrt{AS^2-AH^2}=sqrt{8-4(2-sqrt3)}=sqrt{4sqrt3}=2sqrt[4]3.]
Следовательно, объем пирамиды равен [V=dfrac13cdot SHcdot
S_{ABC}=dfrac2{3sqrt[4]3}.]
Ответ:
(dfrac2{3sqrt[4]3})
Задание
2
#2291
Уровень задания: Равен ЕГЭ
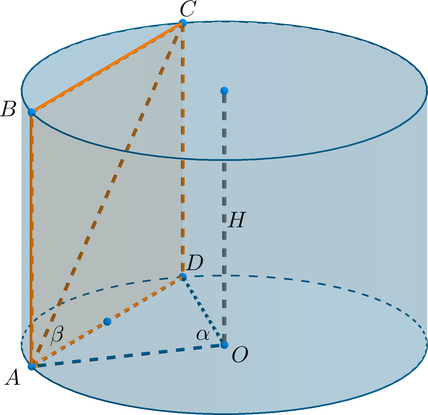
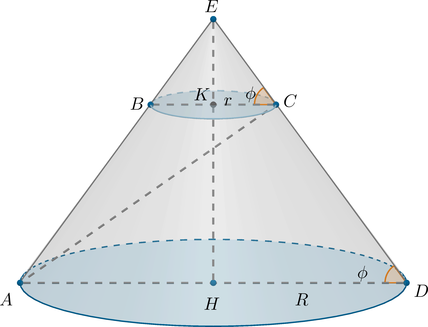
Параллельно оси цилиндра проведена плоскость, отсекающая от окружности основания дугу, градусная мера которой равна (alpha). Диагональ сечения наклонена под углом (beta) к основанию цилиндра.
а) Найдите объем цилиндра, если высота цилиндра равна (H).
б) Вычислите объем цилиндра, если (H=dfrac2{sqrt[3]{pi}}), (alpha=60^circ), (beta=30^circ).
а) Сечение цилиндра данной плоскостью – это прямоугольник (ABCD), где (AB=CD=H).
Дуга (buildrelsmileover{AD}=alpha), следовательно, центральный угол (angle AOD=alpha).
Объем цилиндра равен [V=pi R^2cdot H]
где (R=AO); следовательно, необходимо найти (R^2).
Рассмотрим прямоугольный треугольник (ACD). Из него [mathrm{ctg},beta=dfrac{AD}{CD} quad Rightarrow quad
AD=CDcdot mathrm{ctg},beta=Hcdot mathrm{ctg},beta]
Заметим, что (triangle AOD) – равнобедренный. Тогда по теореме косинусов [AD^2=AO^2+DO^2-2cdot AOcdot DOcdot cosalpha quad
Rightarrow quad (Hmathrm{ctg},beta)^2=2R^2(1-cosalpha)]
Отсюда [R^2=dfrac{H^2mathrm{ctg}^2,beta}{2(1-cosalpha)}]
Следовательно, [V=dfrac{pi
H^3mathrm{ctg}^2,beta}{2(1-cosalpha)}]
б) Подставляя значения из условия, получаем:
[V=dfrac{picdot frac8{pi}cdot (sqrt3)^2}{2left(1-frac12right)}=24.]
Ответ:
б) (24)
Задание
3
#3142
Уровень задания: Сложнее ЕГЭ
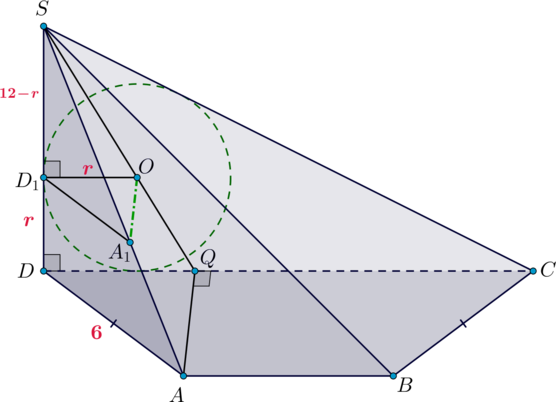
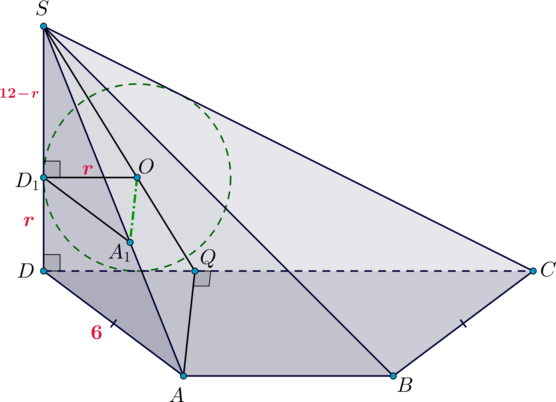
В основании четырехугольной пирамиды (SABCD) лежит равнобедренная трапеция (ABCD), причем (AD=BC=6), (CD>AB). Угол между прямыми (AD) и (BC) равен (60^circ). Известно, что (SD=12) – высота пирамиды.
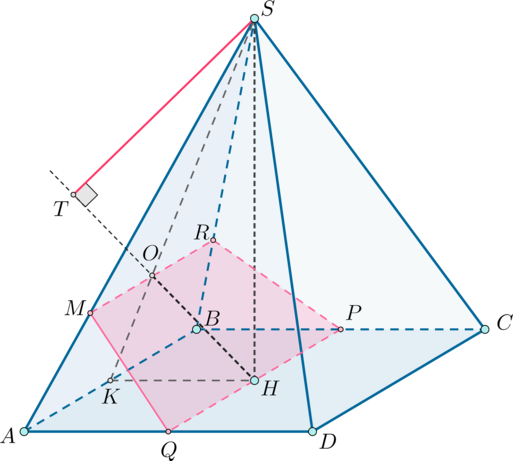
Внутри пирамиды расположен конус так, что основание конуса – вписанная в треугольник (SCD) окружность, а вершина конуса принадлежит ребру (AS). Найдите объем конуса.
Если (E) – точка пересечения прямых (AD) и (BC), то (angle
AEB=60^circ). Так как также (angle BAE=angle ABE) (так как трапеция равнобедренная), то (triangle AEB) равносторонний и (angle BAE=60^circ). Следовательно, и (angle ADC=angle
BCD=60^circ).
Пусть (O) – центр основания конуса, (A_1) – вершина. Тогда (A_1Operp (SCD)).
Заметим, что если в плоскости (ABC) провести (AQperp CD), то (AQperp (SCD)) (так как (AQperp CD) и (AQperp SD)). Следовательно, прямые (A_1O) и (AQ) параллельны, следовательно, лежат в одной плоскости, причем это плоскость (SAQ) (так как (A_1in SA)).
Рассмотрим грань (SCD). Пусть (OD_1perp SD) – радиус вписанной окружности. Тогда (DD_1=r) по свойству прямоугольного треугольника.
(triangle SD_1Osim triangle SDQ), следовательно, [dfrac{SD_1}{SD}=dfrac{D_1O}{DQ} quadRightarrowquad
dfrac{12-r}{12}=dfrac r{DQ}] (DQ) можно найти из прямоугольного (triangle DQA): (DQ) лежит против угла (angle DAQ=30^circ), значит, (DQ=frac12DA=3). Также по теореме Пифагора можно найти (AQ=3sqrt3).
Следовательно, [dfrac{12-r}{12}=dfrac r3 quadRightarrowquad r=dfrac{12}5] Рассмотрим (triangle ASQ): он подобен (triangle A_1SO), значит, [dfrac{A_1O}{AQ}=dfrac{SO}{SQ}=dfrac{SD_1}{SD}=dfrac{frac{48}5}{12}=
dfrac45] Следовательно, (A_1O=frac45AQ=frac{12sqrt3}5).
Тогда объем конуса равен: [V=dfrac13cdot picdot r^2cdot A_1O=dfrac13cdot picdot
left(dfrac{12}5right)^2cdot
dfrac{12sqrt3}5=dfrac{576}{125}sqrt3pi]
Ответ:
(dfrac{576}{125}sqrt3pi)
Задание
4
#2455
Уровень задания: Сложнее ЕГЭ
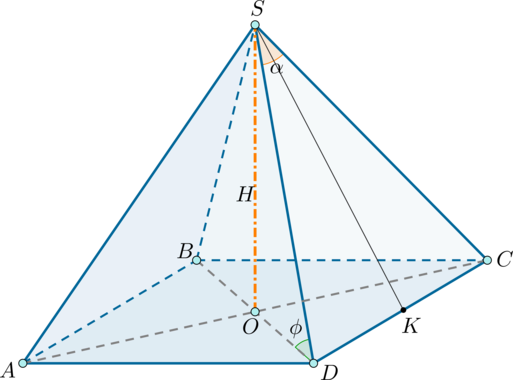
Найдите площадь боковой поверхности правильной четырехугольной пирамиды, высота которой равна (H), а величина плоского угла при вершине равна (alpha). Вычислите эту площадь, если (H=3), (alpha=30^circ).
1) Рассмотрим правильную пирамиду (SABCD), (SO=H) – высота (которая падает в точку пересечения диагоналей основания), (angle
CSD=alpha).
Напомним, что у правильной пирамиды все боковые грани представляют собой равные равнобедренные треугольники.
Введем вспомогательный угол между боковым ребром и основанием: (angle SOD=phi).
Тогда (sinphi=dfrac{SO}{SD}), следовательно, (SD=dfrac{H}{sinphi}=SC).
Тогда, т.к. площадь треугольника равна полупроизведению сторон на синус угла между ними,
[S_{text{бок.пов.}}=4cdot dfrac12SDcdot SCcdot sinalpha=
dfrac{2H^2cdot sinalpha}{sin^2phi}]
2) Теперь необходимо выразить (sinphi) через данные в условии величины.
Проведем (SK) – медиану и высоту в равнобедренном (triangle SCD). Тогда [sinangle
DSK=sindfrac{alpha}2=dfrac{DK}{SD}=dfrac{CD}{2SD} qquad (1)]
(BD=sqrt2cdot CD) как диагональ квадрата, следовательно, (OD=frac{sqrt2}2CD). В (triangle SOD):
[cosphi=dfrac{OD}{SD}=dfrac{CD}{sqrt2SD} qquad (2)]
Разделим равенство ((1)) на равенство ((2)) и получим:
[dfrac{sindfrac{alpha}2}{cosphi}=dfrac1{sqrt2} quad Rightarrow
quad cosphi=sqrt2sindfrac{alpha}2]
Тогда (sin^2phi=1-cos^2phi=1-2sin^2dfrac{alpha}2=cosalpha).
3) Таким образом, [S_{text{бок.пов.}}=dfrac{2H^2sinalpha}{cosalpha}=
2H^2cdot mathrm{tg},alpha.]
4) Подставляя значения из условия, находим, что
[S_{text{бок.пов.}}=6sqrt3.]
Ответ:
(2H^2cdot mathrm{tg},alpha;quad 6sqrt3)
Задание
5
#2454
Уровень задания: Сложнее ЕГЭ
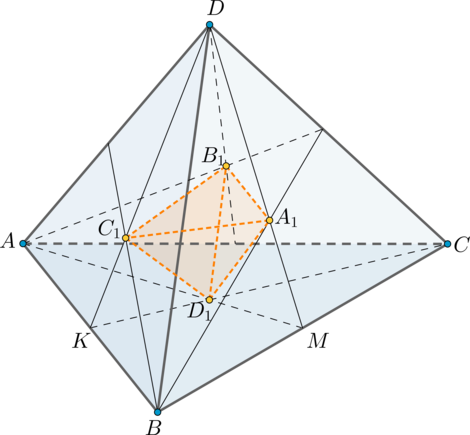
Площадь полной поверхности тетраэдра равна (9). Найдите площадь полной поверхности пирамиды, вершинами которой являются точки пересечения медиан граней данного тетраэдра.
Пусть (DABC) – тетраэдр, точки (A_1, B_1, C_1, D_1) — точки пересечения медиан в гранях (DBC, DAC, DAB, ABC) соответственно.
1) Т.к. медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (DA_1:A_1M=AD_1:D_1M=2:1). Следовательно, (triangle
MADsim triangle MA_1D_1) по углу и двум прилежащим пропорциональным сторонам. Таким образом, (D_1A_1parallel DA) ((angle MA_1D_1=angle MDA) как соответственные) и (D_1A_1=frac13DA).
Аналогичным образом можно доказать, что (D_1B_1=frac13DB), (D_1C_1=frac13DC).
2) (triangle DC_1A_1sim triangle DKM) с коэффициентом (frac23), то есть (C_1A_1=frac23KM). А вот (triangle BKMsim triangle BAC) с коэффициентом (frac12) (т.к. (KM) – средняя линия), то есть (KM=frac12AC).
Следовательно, (C_1A_1=frac23KM=frac23cdot
frac12AC=frac13AC).
Аналогично доказывается, что (A_1B_1=frac13AB), (B_1C_1=frac13BC).
3) Таким образом, все ребра тетраэдра (A_1B_1C_1D_1) в три раза меньше соответствующих ребер тетраэдра (ABCD), а это значит, что каждая грань тетраэдра (A_1B_1C_1D_1) подобна с коэффициентом (frac13) соответствующей грани тетраэдра (ABCD).
4) Т.к. площади подобных треугольников относятся как квадрат коэффициента подобия, то площадь каждой грани тетраэдра (A_1B_1C_1D_1) равна (frac19) от площади соответствующей грани тетраэдра (ABCD). Следовательно,
[S_{A_1B_1C_1D_1}=dfrac19S_{ABCD}=frac19cdot 9=1.]
Ответ: 1
Задание
6
#2292
Уровень задания: Сложнее ЕГЭ
Образующая усеченного конуса составляет с плоскостью нижнего основания угол (phi). Диагональ его осевого сечения перпендикулярна образующей конуса. Сумма длин окружностей оснований равна (2pi
m).
а) Найдите площадь боковой поверхности усеченного конуса.
б) Вычислите эту площадь, если (m=3sqrt2), (phi=arccosfrac15).
а)
1) Достроим усеченный конус до целого конуса. Тогда (EH) – высота, (ED) – образующая всего конуса; (CD) – образующая усеченного конуса, (ABCD) – осевое сечение усеченного конуса, (AC) – диагональ этого сечения, которая перпендикулярна (CD).
(angle EDH=phi) – угол между образующей и плоскостью нижнего основания.
Обозначим за (R) и (r) – радиусы нижнего и верхнего оснований усеченного конуса соответственно. Тогда из условия сумма длин окружностей оснований равна
[2pi m=2pi r+2pi R quad Rightarrow quad R+r=m]
2) Для того, чтобы найти площадь боковой поверхности усеченного конуса, нужно из площади боковой поверхности всего конуса вычесть площадь боковой поверхности маленького конуса:
[S=pi Rcdot ED-pi rcdot EC=pi (Rcdot ED-rcdot EC)]
Заметим, что (triangle EKC) и (triangle EHD) – прямоугольные, следовательно, [cos phi=dfrac{KC}{EC}=dfrac{HD}{ED} quad
Rightarrow quad EC=dfrac{KC}{cos phi}=dfrac{r}{cos phi}
quadtext{ и }quad ED=dfrac{HD}{cos phi}=dfrac{R}{cos phi}]
Значит, площадь боковой поверхности уже приобретает вид:
[S=pileft(dfrac{R^2}{cosphi}-dfrac{r^2}{cosphi}right)=
dfrac{pi}{cosphi}cdot (R-r)(R+r)= dfrac{pi}{cosphi}cdot
mcdot (R-r)]
Необходимо найти (R-r).
3) Т.к. (ACperp CD), то (triangle ACD) – прямоугольный, следовательно, [cos phi=dfrac{CD}{AD} quad Rightarrow quad
CD=ADcdot cos phi=2Rcdot cos phi]
Из данных второго пункта мы можем сказать, что [CD=ED-EC=dfrac{R}{cos phi}-dfrac{r}{cos phi}=dfrac{R-r}{cos phi}]
Таким образом, имеем: [2Rcdot cos phi=dfrac{R-r}{cos phi}
quad Rightarrow quad R(1-2cos^2phi)=r quad Leftrightarrow
quad r=-Rcdot cos2phi]
Но (R+r=m), следовательно, (R-Rcdot cos2phi=m), следовательно, [R=dfrac{m}{1-cos 2phi}]
Подставляя это значение для (R) в (r=-Rcdot cos2phi), находим, что [r=dfrac{mcdot cos 2phi}{cos2phi-1}]
Таким образом, [R-r=dfrac{m(1+cos2phi)}{1-cos2phi}]
4) Значит, площадь боковой поверхности равна
[S=dfrac{pi}{cosphi}cdot
mcdotdfrac{m(1+cos2phi)}{1-cos2phi}=pi m^2cdot
dfrac{1+2cos^2phi-1}{cosphi(1-1+2sin^2phi)}=pi m^2cdot
dfrac{cosphi}{sin^2phi}]
б) Подставляя значения из условия и помня, что (sin^2phi=1-cos^2phi), найдем площадь боковой поверхности:
[S=picdot (3sqrt2)^2cdot
dfrac{cosleft(arccosfrac15right)}{1-cos^2left(arccosfrac15right)}=
dfrac{15}4pi=3,75pi]
Ответ:
а) (pi m^2cdot
dfrac{cosphi}{sin^2phi})
б) (3,75pi)

УСТАЛ? Просто отдохни