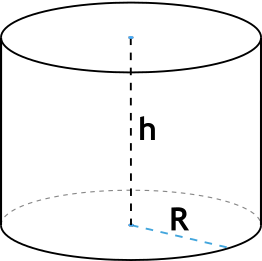
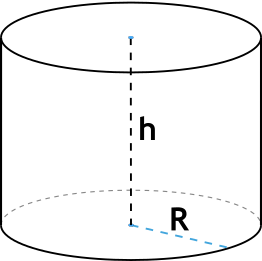
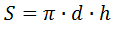В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
-
Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
Чтобы найти площадь поверхности цилиндра необходимо знать радиус его основания и высоту. Очень важно понимать, что существует две поверхности — боковая и полная. Площадь боковой поверхности включает в себя площадь поверхности цилиндра без учета площади его оснований. Полная же площадь основания цилиндра включает как площадь боковой поверхности, так и обоих оснований цилиндра.
На нашем сайте вы можете рассчитать и объем цилиндра
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые её пересекают.
Содержание:
- калькулятор площади поверхности цилиндра
- формула площади поверхности цилиндра
- формула площади боковой поверхности цилиндра
- примеры задач
Формула площади поверхности цилиндра
{S_{полн} = 2pi R(h+R)}
R — радиус основания цилиндра
h — высота цилиндра
Формула площади боковой поверхности цилиндра
{S_{бок} = 2pi Rh}
R — радиус основания цилиндра
h — высота цилиндра
Примеры задач на нахождение площади поверхности цилиндра
Задача 1
Найдите площадь поверхности цилиндра если его высота равна 5см а радиус 6см.
Решение
Так как необходимо найти площадь полной поверхности цилиндра, воспользуемся первой формулой. Подставим в нее значения из условия и произведем вычисления.
S_{полн} = 2pi R(h+R) = 2pi cdot 6(5+6) = 12pi cdot 11 = 132 pi : см^2 approx 414.69023 : см^2
Ответ: 132 pi : см^2 approx 414.69023 : см^2
Чтобы проверить правильность ответа можно использовать калькулятор .
Задача 2
Найдите площадь боковой поверхности цилиндра, если радиус основания равен 2см а высота 7см.
Решение
Для решения этой задачи нам потребуется вторая формула.
S_{бок} = 2pi Rh = 2pi cdot 2 cdot 7 = 28 pi : см^2 approx 87.96459 : см^2
Ответ: 28 pi : см^2 approx 87.96459 : см^2
Осталось убедиться, что задача решена верно, для этого используем калькулятор .
Этот онлайн калькулятор площади боковой поверхности цилиндра поможет быстро и точно найти площадь только боковой поверхности цилиндра. При этом площадь оснований цилиндра не учитывается.
Калькулятор площади боковой поверхности цилиндра позволяет сделать расчет двумя различными способами. Выбор которго зависит от предоставленных данных о цилиндре.
Сделав расчет площади боковой поверхности цилиндра на этом калькуляторе Вы получите детальное пошаговое решение с выводом формул и промежуточных результатов, и также полный ответ.
- Калькулятор
- Инструкция
- Теория
- История
- Сообщить о проблеме

Способ расчета площади боковой поверхности цилиндра:
Диаметр d:
Высота h:
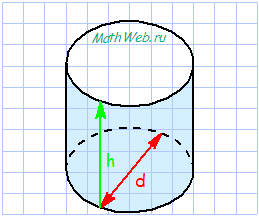
Площадь боковой поверхности цилидра в развретке предстваляет из себя прямоугольник.
Формула площади боковой поверхности цилиндра
где d — диаметр основания, h — высота цилиндра.
Решение:
S = π·d·h
= π·12.8·3.5
= π·44.8
= 44.8·π
=
140.739
Ответ: Площадь боковой поверхности цилидра с диаметром основания 12.8 и высотой 3.5 равна 140.739
Цилиндрическая поверхность называется боковой поверхностью цилиндра. Две параллельные поверхности называются основаниями цилиндра.
Площадью боковой поверхности цилидра является прямоугольник, который получается путем развертки боковой поверхности в плоскость.
Скачать все формулы нахождения площади поверхности цилиндра в формате Word/PDF
Похожие калькуляторы
-
Площадь поверхности цилиндра онлайн калькулятор (2 способа)
-
Объём цилиндра онлайн калькулятор (3 способа)
-
Площадь поверхности призмы онлайн калькулятор
-
Площадь поверхности параллелепипеда онлайн калькулятор
-
Площадь поверхности цилиндра онлайн калькулятор (2 способа)
Калькуляторы других категорий
-
Деление в столбик онлайн. Калькулятор наглядного деления.
-
Сторона треугольника 14 формул расчет онлайн
-
Перевод чисел из одной системы счисления в любую другую онлайн
-
Сложение, умножение и деление чисел в различных системах счисления
-
Умножение в столбик онлайн. Калькулятор наглядного умножения.
| Ваша оценка? |
Как рассчитать площадь цилиндра
На данной странице калькулятор поможет рассчитать площадь поверхности цилиндра онлайн. Для расчета задайте высоту и радиус.
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Боковая поверхность
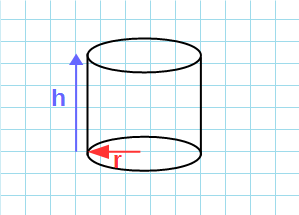
Формула площадь боковой поверхности цилиндра через высоту и радиус:
π — константа равная (3.14); r — радиус основания; h — высота цилиндра.
Полная поверхность

Формула площадь полной поверхности цилиндра через высоту и радиус:
π — константа равная (3.14); r — радиус основания; h — высота цилиндра.
Площадь поверхности цилиндра
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности цилиндра
Чтобы посчитать площадь поверхности цилиндра воспользуйтесь нашим очень удобным онлайн калькулятором:
Площадь боковой поверхности
Высота цилиндра h =
=
Площадь боковой поверхности цилиндра Sбпц =
0
Округление ответа: Округление числа π:
Площадь полной поверхности
Высота цилиндра h =
=
Площадь полной поверхности цилиндра Sппц =
0
Округление ответа: Округление числа π:
Просто введите данные и получите ответ.
Теория
Площадь боковой поверхности цилиндра
Как вычислить площадь боковой поверхности цилиндра Sбпц, зная высоту цилиндра h и его радиус r (или диаметр d)?
Формулы
Через радиус:
Sбпц = 2⋅π⋅r⋅h
Через диаметр:
Sбпц = π⋅d⋅h
Пример #1
К примеру, посчитаем площадь боковой поверхности цилиндра с высотой 5 см и радиусом 1.5 см:
Sбпц = 2 ⋅ 3.14 ⋅ 1.5 ⋅ 5 = 6.28 ⋅ 7.5 = 47.1 см²
Пример #2
Посчитаем площадь боковой поверхности цилиндра с высотой 10 см и диаметром 4 см:
Sбпц = 3.14 ⋅ 4 ⋅ 10 = 125.6 см²
Площадь полной поверхности цилиндра
Как вычислить площадь полной поверхности цилиндра Sппц, зная высоту цилиндра h и его радиус r (или диаметр d)?
Формулы
Через радиус:
Sппц = 2⋅π⋅r⋅(h+r)
Через диаметр:
Sппц = π⋅d²2 + π⋅d⋅h
Пример #1
К примеру, посчитаем площадь полной поверхности цилиндра с высотой 8 см и радиусом 2 см:
Sппц = 2 ⋅ 3.14 ⋅ 2 ⋅ (8+2) = 6.28 ⋅ 2 ⋅ 10 = 125.6 см²
Пример #2
Посчитаем площадь полной поверхности цилиндра с высотой 2 м и диаметром 0.5 м:
Sппц = 3.14⋅0.5²2 + 3.14⋅0.5⋅2 = 0.3925 + 3.14 = 3.5325 м²