Строение атома
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: планетарная модель атома.
Атомы каждого химического элемента имеют строго индивидуальный линейчатый спектр, присущий только данному элементу и не меняющийся от опыта к опыту. Как это можно объяснить? Как вывести формулу, дающую весь набор частот атомного спектра? Чтобы сделать это, нужно узнать, как устроен атом.
Модель Томсона
Первую модель строения атома придумал английский физик Джозеф Джон Томсон (удостоенный Нобелевской премии за открытие электрона). В конечном счёте она оказалась неверной, но сыграла важную роль, будучи стимулом последующих экспериментальных исследований Резерфорда. Физики называли модель Томсона «пудинг с изюмом».
Согласно Томсону атом представляет собой шар размером порядка см. По этому шару некоторым образом распределён положительный заряд, а внутри шара, подобно изюминкам, находятся электроны (рис. 1).
Рис. 1. Модель атома Томсона
Суммарный заряд электронов в точности равен положительному заряду шара, поэтому атом в целом электрически нейтрален.
Излучение атомов объясняется колебаниями электронов около положений равновесия (как вы помните, любой ускоренно движущийся заряд излучает электромагнитные волны). Однако вся совокупность экспериментальных данных по атомным спектрам не укладывалась в модель Томсона. Например, для некоторых химических элементов были подобраны формулы, хорошо описывающие их спектры, но эти формулы из модели Томсона никак не следовали.
Опыты Резерфорда
Верна ли модель Томсона? Как в действительности распределены положительные и отрицательные заряды внутри атома? Чтобы ответить на эти вопросы, нужен был эксперимент, позволяющий проникнуть внутрь атома. Ученик Томсона, знаменитый английский физик Эрнест Резерфорд предложил с этой целью бомбардировать атом высокоэнергетичными ?-частицами и смотреть, как они будут отклоняться положительным зарядом атома.
Что такое -частицы? Потоки этих частиц — так называемые «альфа-лучи» — были обнаружены при радиоактивном распаде некоторых элементов (например, радия). В результате тщательных исследований, проведённых опять-таки Резерфордом, было установлено, что каждая
-частица имеет положительный заряд, равный по модулю удвоенному заряду электрона, и массу, превышающую массу электрона примерно в
раз. То есть,
-частица оказалась полностью ионизованным (лишённым электронов) атомом гелия.
Резерфорд говорил об -частицах как об ионах гелия; сейчас мы знаем, что это ядра гелия.
Но в те времена об атомных ядрах ещё ничего не знали — о них Резерфорду лишь предстояло догадаться, глядя на результаты своих знаменитых опытов!
Энергия -частиц очень велика — достаточно сказать, что скорость их вылета из радиоактивного образца составляет примерно
скорости света. Поэтому интересно было выяснить, на какие углы будут отклоняться столь мощные «снаряды» при рассеянии на отдельных атомах, а точнее — на их положительных зарядах.
Пучок -частиц направлялся на тончайшую золотую фольгу. Как гласит история, Резерфорд не сомневался в том, что углы отклонения должны быть весьма малы: имея столь огромную энергию,
-частицы должны проходить сквозь фольгу как нож сквозь масло. Только «для очистки совести», на всякий случай, он попросил учеников посмотреть, не возникает ли рассеяния
-частиц на большие углы.
Каково же было всеобщее удивление, когда такие частицы обнаружились! Да, как и следовало ожидать, подавляющая доля -частиц отклонялась несущественно. Но совсем небольшая их часть (примерно одна частица из нескольких тысяч) отклонялась на угол, больший
(рис. 2).
Рис. 2. Рассеяние -частиц на атомах
Эти отклонения казались совершенно невероятными. По словам Резерфорда, дело выглядело так, словно артиллерийский снаряд налетел на кусок бумаги и от удара повернул назад.
А «бумагой» в образном сравнении Резерфорда служил атом, устроенный согласно модели Томсона. Действительно, допустим, что положительный заряд атома «размазан» по всему атому, то есть шару радиусом
см. Этот положительный заряд создаёт электрическое поле, тормозящее и отклоняющее
-частицы. Вблизи атома потенциал данного поля:
Расчёты, однако, показывают, что такое поле оказывается слишком слабым — его тормозящего действия никак не хватит для того, чтобы остановить -частицу и отбросить её назад!
Таким образом, наличие -частиц, отброшенных фольгой, опровергло модель Томсона. Что же было предложено взамен?
Планетарная модель атома
Чтобы отбросить -частицу, положительный заряд атома должен создавать куда более сильное электрическое поле, чем то, которое получается в модели Томсона. А чтобы создать такое поле, положительный заряд должен быть сосредоточен в области, гораздо меньшей размера атома.
Размер этой области можно вычислить. Если положительный заряд занимает область размером
, то вблизи заряда создаётся электрическое поле с потенциалом
Зная кинетическую энергию -частицы, можно найти величину тормозящего потенциала
, а затем и размер
положительно заряженной области. Вычисления, проведённые Резерфордом, дали следующий результат:
см.
Эта величина на пять порядков (в сто тысяч раз!) меньше размера атома. Так на смену модели Томсона пришла планетарная модель атома (рис. 3).
Рис. 3. Планетарная модель атома
В центре атома находится крошечное положительно заряженное ядро, вокруг которого, словно планеты вокруг Солнца, движутся электроны. Между ядром и электронами действуют силы кулоновского притяжения, но упасть на ядро электроны не могут за счёт своего движения — точно так же, как и планеты не падают на Солнце, хоть и притягиваются к нему.
Заряд ядра по модулю равен суммарному заряду электронов, так что атом в целом электрически нейтрален. Однако электроны могут быть выбиты из своих орбит и покинуть атом — тогда атом превращается в положительно заряженный ион.
Масса электронов составляет очень малую часть общей массы атома. Например, в атоме водорода всего один электрон, и его масса в раз меньше массы ядра. Следовательно, почти вся масса атома сосредоточена в ядре — и это при том, что ядро в сто тысяч раз меньше самого атома.
Чтобы лучше почувствовать соотношение масштабов атома и ядра, представьте себе, что атом стал размером с Останкинскую телебашню ( м). Тогда ядро окажется горошиной размером
мм, лежащей у вас на ладони. И тем не менее, почти вся масса атома заключена в этой горошине!
Разберем задачи ЕГЭ по темам: «Строение атома», «Энергетические уровни», «Ядро атома», «Электронные оболочки», «Протоны и нейтроны».
Задача 1.
Ядро элемента претерпевает альфа-распад. Как изменятся следующие физические величины: зарядовое число, массовое число у образовавшегося (дочернего) ядра по отношению к исходному?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Зарядовое число | Массовое число |
| 1 | 1 |
Решение:
При решении подобных задач выделяют следующие виды радиоактивных распадов:
1) α-распад (альфа-распад) – распад ядер, сопровождающийся выбросом α-частицы, которая является ядром атома гелия ;
2) β-распад (бета-распад) – распад ядер, сопровождающийся выбросом β-частицы, которая является электроном ;
3) γ-распад (гамма-распад) – распад ядер, сопровождающийся выбросом γ-квантов, не имеющих заряда и массы.
Составление ядерных реакций основывается на законах сохранения заряда и массы. Таким образом, суммарное зарядовое число в левой части уравнения должно быть равно суммарному зарядовому числу в правой части уравнения. То же самое относится и к массовому числу.
Запишем ядерную реакцию для данной задачи.
.
Уменьшение зарядового числа Z произошло на 2 единицы, а массового числа на 4 единицы.
| Зарядовое число | Массовое число |
| 2 | 2 |
Ответ: 22
Задача 2.
Как изменяются с уменьшением массового числа изотопов одного и того же элемента число нейтронов в ядре и число электронов в электронной оболочке соответствующего нейтрального атома?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в ответ выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Число нейтронов в ядре | Число электронов в электронной оболочке нейтрального атома |
| 1 | 1 |
Решение:
Изотопы – это атомы одного и того же химического элемента, отличающиеся количеством нейтронов в атомном ядре. Количество протонов у всех изотопов данного химического элемента одинаковое.
Массовое число определяется суммой масс протонов и нейтронов. Масса электронов не влияет на массу атома, при этом считается, что вся масса атома сосредоточена в ядре.
При уменьшении массового числа изотопов одного и того же элемента число нейтронов в ядре, соответственно, уменьшается. Число электронов в электронной оболочке нейтрального атома остается неизменным. Так как атом нейтральный, то количество протонов и количество электронов будут равны между собой.
| Число нейтронов в ядре | Число электронов в электронной оболочке нейтрального атома |
| 2 | 3 |
Ответ: 23
Задача 3.
Для некоторых атомов характерной особенностью является возможность захвата атомным ядром одного из ближайших к нему электронов. Как при захвате электрона изменяются массовое число атомного ядра и число нейтронов в ядре?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Массовое число ядра | Число нейтронов в ядре |
| 1 | 1 |
Решение:
При захвате ядром одного из электронов происходит превращение протона в нейтрон. Так как массовое число ядра определяется количеством протонов и нейтронов, то увеличение числа нейтронов на единицу и уменьшение числа протонов на единицу, не изменит конечного результата. Поэтому массовое число ядра не изменится.
Превращение протона в нейтрон увеличит общее количество нейтронов в ядре.
| Массовое число ядра | Число нейтронов в ядре |
| 3 | 1 |
Ответ: 31
Задача 4.
В первом эксперименте атомы водорода облучают потоком фотонов такой частоты, что электроны в атомах переходят с энергетического уровня с номером n > 1 на энергетический уровень с номером n + 1. При постановке второго эксперимента частоту фотонов подбирают такой, что электроны в атомах переходят с энергетического уровня с номером n − 1 на энергетический уровень с номером n. Определите, как изменяются во втором эксперименте по сравнению с первым длина волны падающего на атом фотона и приращение энергии атома в результате поглощения фотона.
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Длина волны падающего на атом фотона |
Приращение энергии атома в результате поглощения фотона |
| 1 | 1 |
Решение:
Рассчитаем энергию поглощенного фотона при переходе с уровня n на уровень n+1. Для этого воспользуемся формулой энергетических уровней атома водорода.
Для второго перехода с уровня n-1 на уровень n этот переход можно представить в виде:
Найдем разность этих энергий:
Преобразовав это выражение, получим:
Разность этих энергий отрицательная, так как числитель (по условию n > 1). Поэтому энергия фотона во втором переходе больше, чем в первом.
Согласно формуле Планка, увеличение энергии соответствует уменьшению длины волны.
| Длина волны падающего на атом фотона |
Приращение энергии атома в результате поглощения фотона |
| 2 | 1 |
Ответ: 21
Вот таким удивительным объектом оказался атом. Однако планетарная модель атома, объяснив результаты опытов Резерфорда по рассеянию -частиц, оказалась лишь первым шагом на пути к пониманию внутриатомных процессов. А именно, планетарная модель приводила к одному серьёзному противоречию, и преодоление этого противоречия Нильсом Бором положило начало физике атома. Читаем следующий листок!
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Строение атома» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 октября 2015;
проверки требует 1 правка.
Планетарная модель атома: ядро (красное) и электроны (зелёные)
Планета́рная моде́ль а́тома, или модель атома Резерфорда — исторически важная модель строения атома предложенная Эрнстом Резерфордом в классической статье, опубликованной в 1911 г. на основании анализа и статистической обработке результатов экспериментов по рассеиванию альфа-частиц в тонкой золотой фольге, выполненных Гейгером и Марсденом в 1909 г.
В этой модели Резерфорд описывает атом состоящим из крохотного положительно заряженного ядра, в котором сосредоточена почти вся масса атома, вокруг которого вращаются электроны, — подобно тому, как планеты движутся вокруг Солнца.
Планетарная модель атома соответствует современным представлениям о строении атома с уточнениями, что движение электронов не может быть описано законами классической механики и имеет квантовомеханическое описание.
Исторически, планетарная модель Резерфорда пришла на смену «модели сливового пудинга» Джозефа Джона Томсона, которая предполагает, что отрицательно заряженные электроны помещены внутрь положительно заряженного атома с распределённым по всему объему атома положительным зарядом, подобно изюминкам в пироге.
Предыстория[править | править вики-текст]
К 1904 году японский физик Нагаока разработал раннюю, как оказалось впоследствии, ошибочную «планетарную модель» атома («атом типа Сатурна»)[1]. Модель была построена на аналогии с расчётами устойчивости колец Сатурна (кольца уравновешены из-за очень большой массы планеты). Модель Нагаоки была неверна, но два следствия из нее оказались пророческими:
- ядро атома действительно очень массивно;
- электроны удерживаются на орбите благодаря электростатическим силам (подобно тому, как кольца Сатурна удерживаются гравитационными силами).
Новую модель строения атома Резерфорд предложил в 1911 году анализом экспериментов по рассеиванию альфа-частиц в золотой фольге, проведённого под его руководством[2].
При этом рассеянии большое, неожиданно статистически необъяснимое, количество альфа-частиц рассеивалось на большие углы, что свидетельствовало о том, что центр рассеяния имеет небольшие размеры, в нём сосредоточен значительный электрический заряд и масса атома.
Расчёты Резерфорда показали, что рассеивающий центр, заряженный положительно или отрицательно, должен быть по крайней мере в 3000 раз меньше размера атома, который в то время уже был известен и оценивался как примерно 10−10 м. Поскольку в то время электроны уже были известны, а их масса и заряд определены, то рассеивающий центр, который позже назвали ядром, должен был иметь противоположный электронам заряд. Резерфорд не связал величину заряда с атомным номером. Этот вывод был сделан позже. А сам Резерфорд предположил, что заряд ядра пропорционален атомной массе. Связь электрического заряда ядра с атомным номером химического элемента установил Генри Мозли в экспериментах, выполненных в 1913 г.
Недостатком планетарной модели была невозможность объяснения ею устойчивости атомов. Из классической электродинамики следует, что если электроны движутся вокруг ядра, испытывая центростремтельное ускорение как планеты вокруг Солнца, то они по законам классической электродинамики должны были бы излучать электромагнитные волны, терять орбитальную энергию движения и в результате упасть на ядро.
Это противоречие было снято следующим шагом в развитии планетарной модели (модель Бора), постулирующая другие, отличные от классических законы движения электронов. Полностью, противоречащие эксперименту, выводы классической электродинамики смогло решить развитие квантовой механики.
Примечания[править | править вики-текст]
- ↑ Bryson Bill. A Short History of Nearly Everything. — Broadway Books. — ISBN 0767908171.
- ↑ E. Rutherford, The Scattering of α and β Particles by Matter and the Structure of the Atom, Philosophical Magazine. Series 6, vol. 21. May 1911
FAQ
Планетарная модель атома
Физик Михаил Высоцкий об открытии ядра атома, модели атома Бора и принципе неопределенности Гейзенберга
Над материалом работали
Коржуев А. Планетарная модель атома и теория Бора: история, гипотезы, эксперимент //Квант. — 1997. — № 2. — С. 18-20.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Заканчивается XX век. Как он будет назван: веком электроники, авиации, компьютеров? Трудно сказать, но наверняка физики XXI века, оглядываясь в прошлое, назовут его веком квантовой механики, возникновению которой и предшествовали открытия, связанные с «устройством» атома и его закономерностях. О них мы и поговорим.
Немного истории
Начнем со спектроскопии. В 1859 году Г.Кирхгоф и Р.Бунзен разработали метод спектрального анализа и объяснили, в частности, происхождение четырех темных линий поглощения в спектре Солнца. Их обнаружил еще в 1814 году Й.Фраунгофер, а теперь, 45 лет спустя, было показано, что эти линии хорошо совпадают с яркими линиями в спектрах, испускаемых накаленными газами и парами различных веществ в обычных земных условиях. В 1885 году И.Бальмер опубликовал статью, в которой установил, что длины волн этих линий с хорошей точностью подчиняются формуле
(~lambda = k dfrac{m^2}{m^2 — 2^2},)
где m = 3,4,5 и 6, а k — некоторая постоянная, и могут быть приписаны водороду. Вскоре были обнаружены еще пять линий водорода, но уже в ультрафиолетовой области солнечного спектра поглощения, и их длины волн также с хорошей точностью укладывались в формулу Бальмера. Кстати, эта формула в 1890 году была переписана Ю.Ридбергом для волновых чисел:
(~nu^* = dfrac{1}{lambda} = dfrac{nu}{c} = dfrac 4k left(dfrac{1}{2^2} — dfrac{1}{m^2} right).)
Коэффициент (~dfrac 4k) получил название постоянной Ридберга R (по современным данным R = 10973731,77 м-1). Затем обнаружили целых три серии линий в инфракрасной области спектра атома водорода, которые тоже охватывались упомянутой формулой. И вообще, как оказалось, все пять серий линий можно описать одной формулой — формулой Бальмера — Ридберга
(~nu^* = R left(dfrac{1}{n^2} — dfrac{1}{m^2} right),)
где для каждой серии число n свое: n = 1, 2, 3, 4, 5, а внутри серии число m принимает ряд значений, начиная с n + 1. Однако, фундаментального физического обоснования закономерностей линейчатых спектров в то время не было. В частности, существовавшая «пудинговая» модель атома Дж.Дж.Томсона, согласно которой отрицательно заряженные электроны, как изюминки в пудинге, были распределены в неком жидком положительно заряженном веществе, к указанным результатам не приводила.
Теперь следует вспомнить о том, что в 1900 году М.Планку для объяснения закономерностей теплового излучения пришлось выдвинуть идею о квантовой, дискретной структуре излучения и распространения света (уже имевшую, кстати сказать, к моменту рождения «экспериментальное подтверждение» — еще в 1887 году Г. Герц наблюдал внешний фотоэффект), и не забыть о явлениях, также подтверждавших сложное строение атома, — открытии Дж.Дж.Томсоном электрона, обнаружении радиоактивности и термоэлектронной эмиссии.
Что же было общим для всех этих явлений? Очевидно, то, что они не могли быть удовлетворительно объяснены, исходя из существовавших в то время представлений о строении атома. Однако (и история физики это подтверждает) накопление такого рода фактов может происходить достаточно долго, пока не произойдет «скачок» — такое событие в истории науки, которое вынесет окончательный приговор либо в пользу накопившихся фактов, либо в пользу опровергаемой ими теории. Таким «скачком» в истории атома стали опыты Резерфорда, которые легли в основу создания новой теории строения атома.
Опыты Резерфорда
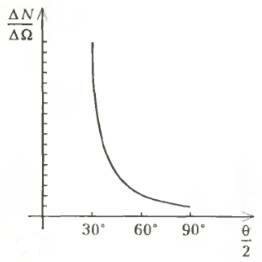
Еще с 1906 года Э.Резерфорд изучал прохождение α-частиц через различные по своим свойствам вещества, а в декабре 1910 года им была выведена формула, описывающая рассеяние α-частиц. Из формулы следовало, что для конкретного источника (с заданными плотностью потока и кинетической энергией частиц) число частиц ΔN, рассеивающихся в телесном угле ΔΩ, связано с углом рассеяния θ соотношением
(~dfrac{Delta N}{Delta Omega} sim dfrac{1}{sin^4 dfrac{theta}{2}} .)
Соответствующий график изображен на рисунке 1 (коэффициент пропорциональности условно принят за 1).
Рис. 1
Помощники Резерфорда (Гейгер и Марсден) провели многие недели в полной темноте, регистрируя вспышки рассеянных фольгой α-частиц на люминесцирующих экранах (они насчитали около двух миллионов различных актов рассеяния). И что же? Оказалось, что некоторые частицы (хотя их относительно мало) отклоняются на очень большие углы — иногда больше 90°, а согласно Томсону такого быть не должно. Полученные данные неопровержимо свидетельствовали о том, что о «пудинге» не может быть и речи. В мае 1911 года Резерфорд впервые опубликовал свои результаты в статье «Рассеяние α-частиц веществом и строение атома», в которой увидела свет ядерная модель атома и обсуждалось ее резкое противоречие модели атома Томсона. Атом по Резерфорду подобен планетарной системе: тяжелое положительно заряженное ядро (Солнце) и вращающиеся по орбитам вокруг него электроны (планеты).
Зададимся, однако, вопросом: был ли Резерфорд одинок в своем отрицании «пудинговой» модели? Неужели никто больше не видел всей сложности противоречий в вопросе о строении атома и не пытался как-то изменить эту модель? История физики свидетельствует: такие попытки были, и были задолго до 1911 года. Например, французский физик Ж.Перрен еще в 1901 году упоминал в своих лекциях о возможности существования ядерно-планетарной структуры атома. А в 1904 году модель сатурноподобного атома предложил японец Х.Нагаока: центральную положительную частицу окружало в его атоме кольцо электронов, двигавшихся с одной и той же угловой скоростью (чем не Сатурн с кольцами?). Неизвестно точно, встречался ли Резерфорд с Нагаокой (который путешествовал примерно в это время по Европе и был даже в Манчестере), но в указанной статье ссылки на эту модель есть. Еще одна, интересная на наш взгляд, аналогичная модель была предложена английским астрофизиком Дж.Никольсоном примерно в 1911 — 1912 годах — он построил ее для объяснения ряда линий непонятного происхождения в спектрах туманностей.
Список можно было бы и продолжить. Однако вернемся к опытам Резерфорда и его статье. Ряд фраз из нее свидетельствовали о том, что сам исследователь не мог не понимать, что его модель противоречит классической электродинамике Максвелла — поскольку ускоренно движущийся заряд должен непрерывно излучать, электрон (в планетарной модели) должен очень быстро упасть на ядро, всего за 10-8 с. Как же тогда может идти речь об устойчивости атома? Да и спектр излучения по классическим представлениям должен быть непрерывным (а не линейчатым), так как частота обращения должна непрерывно меняться. Ядерно-планетарная модель, таким образом, до предела обостряла противоречие теории с наблюдаемой устойчивостью атома. Ситуация возникла драматическая, и самому Резерфорду не было суждено выпутаться из всех противоречий. А выход, тем не менее, был найден.
Гипотеза Бора
Нильс Бор (1885-1962)
Незаурядность Нильса Бора как ученого проявилась довольно рано. В 1905 году, будучи еще студентом Копенгагенского университета, он исследовал колебания струй жидкости с целью измерения коэффициента поверхностного натяжения и был удостоен за работу золотой медали. Магистерскую диссертацию Бор посвятил электронной теории металлов (1909 г.), а затем приступил к докторской диссертации и доказал принципиальную невозможность создания теории магнитных свойств вещества на основе только классических представлений (1911 г.). После защиты диссертации ученый отправляется в Кембридж на годичную стажировку к Дж. Дж.Томсону, где в октябре 1911 года на Кавендишском обеде знакомится с Резерфордом и получает право поработать у него в Манчестерской лаборатории. В это время (весна- осень 1912 г.) Бор и приходит к мысли о том, что из противоречия ядерно-планетарной модели и классической электродинамики придется выбираться с помощью квантовых представлений Планка.
Вернувшись после стажировки в Копенгаген, Бор интенсивно работает и к марту 1913 года готовит три статьи, в которых содержатся основы всей его теории. В сентябре 1913 года Бор выступает с докладом о своих новых результатах в Бирмингеме на заседании Британской ассоциации развития науки. Аудитория — самая авторитетная и взыскательная: корифеи классической физики Рэлей, Джине, Лоренц, Томсон. Доклад был принят патриархами науки весьма прохладно и иронично (лорд Рэлей ограничился лишь замечанием, что людям, которым за 60, уже нет смысла высказывать суждения о новых идеях). Положение изменилось в благоприятную сторону лишь после публикации ряда статей в научных журналах. Первым поддержал Бора Дж.Джине: «Доктор Бор дал в высшей степени остроумное, плодотворное и — я думаю … — убедительное объяснение закономерностей в спектральных линиях».
Как уже было сказано, к середине второго десятилетия XX века в физике утвердилась идея Планка о дискретном характере энергии атомов, а также идея Эйнштейна о квантовой структуре атома. Что же сделал Бор? Прежде всего он добавил положение о том, что следует отказаться от важнейшего вывода классической электродинамики о непрерывном характере излучения энергии электроном, движущимся вокруг ядра. Взамен были предложены стационарные состояния атома, в которых излучения нет, и возможность перехода между ними либо с излучением, либо с поглощением энергии. Естественно, чтобы решиться на такой шаг, требовалось большое научное мужество. Бор им обладал.
Впоследствии из принятых Бором допущений остались два известных его постулата и правило квантования орбит. Из выражения для энергии электрона, движущегося по орбите,
(~W = dfrac{m upsilon^2}{2} — dfrac{ze^2}{4 pi varepsilon_0 r})
и уравнения второго закона Ньютона
(~dfrac{m upsilon^2}{r} = dfrac{ze^2}{4 pi varepsilon_0 r^2},)
а также используя идею квантования момента импульса в стационарном состоянии
(~m upsilon r = dfrac{h}{2 pi} n,)
легко получить знаменитую боровскую формулу для энергии электрона в атоме:
(~W_n = -dfrac{mz^2e^4}{4 varepsilon^2_0 h^2 n^2} .)
Эта энергия, как видно, представляет собой квантованную величину (принимает дискретный ряд значений, соответствующих целочисленным n = 1, 2, …). Сам Бор писал об этом так: «Разным n соответствуют ряд значений Wn, соответствующих различным конфигурациям системы, в которых нет излучения, а потому они будут стационарными, пока система не будет возмущена извне».
Интересно, что еще в начале февраля 1913 года по совету одного из коллег Бор сопоставил свой результат с формулой Бальмера — Ридберга для спектра атома водорода (до этого он о ней ничего не знал) и предположил, что так называемые спектральные термы — величины (~dfrac{R}{n^2}) и (~dfrac{R}{m^2}) — пропорциональны энергии электрона в атоме в разных стационарных состояниях. Следующий шаг — предположение о том, что при переходе атома из одного стационарного состояния в другое излучается один квант энергии, откуда и получается знаменитое правило частот (фактически второй постулат Бора)
(~h nu_{n_1 to n_2} = W_{n1} — W_{n2},)
(~nu = dfrac{mz^2e^4}{4 varepsilon^2_0 h^3} left(dfrac{1}{n^2_2} — dfrac{1}{n^2_1} right).)
Совпадение с формулой Бальмера — Ридберга абсолютное, что говорит о хорошем согласии теории с экспериментом. Сохранилось свидетельство известного физика Д.Хевеши о том, что когда об этом блестящем подтверждении теории Бора узнал Эйнштейн, он был потрясен тем фактом, что частота излучения, оказывается, не зависит от частоты вращения электрона в атоме: «Большие глаза Эйнштейна стали еще больше, и он сказал мне: «Тогда это одно из величайших открытий».
Сам же Бор в введении к статье «Связывание электрона положительным ядром» пишет о той большой роли, которую играет в его теории постоянная Планка: «Только существование кванта действия h препятствует слиянию электронов с ядрами в нейтральную частицу практически бесконечно малого размера… Только оно одно дало полное объяснение замечательным зависимостям между физическими и химическими свойствами элементов — зависимостям, выраженным в периодической таблице Менделеева».
Принцип соответствия
Отрицая классическую электродинамику, Бор тем не менее все время пытается найти связь между новой и старой теориями и в 1912 году формулирует свой знаменитый принцип соответствия. Согласно этому принципу, физическая теория, явившаяся обобщением и развитием некоторой классической теории, в ряде предельных случаев должна давать результаты, совпадающие с классическими.
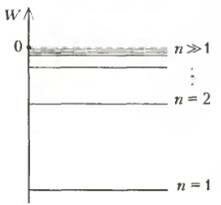
В боровской теории атома это следует понимать так: при больших квантовых числах п выводы теории должны соответствовать классическим представлениям. Для атома водорода, например, при больших квантовых числах «расстояния» между соседними энергетическими уровнями оказываются очень малыми (рис. 2), т.е. уровни становятся квазинепрерывными — это и есть отброшенные классические представления. В работе «О спектре водорода» Бор с помощью этого принципа вычисляет постоянную Ридберга. Попробуйте самостоятельно воспроизвести ход его мыслей.
Рис. 2
Теория и эксперимент
Может ли какой-нибудь эксперимент подтвердить результаты теории? Слово А.Эйнштейну: «Опыт никогда не скажет теории «да», но говорит в лучшем случае «может быть», большей частью — просто «нет». Когда опыт согласуется с теорией, для нее это означает «может быть», когда же противоречит ей, объявляется приговор «нет». Таким образом, суждение о том, сколько и каких экспериментов необходимо, чтобы подтвердить истинность теории, не может быть абсолютно безупречным — чем их больше, тем больше у исследователя степень уверенности, что теория достоверна. Но абсолютной уверенности нет никогда — на определенном этапе разработки проблемы может «подвернуться» факт, экспериментальный результат, противоречащий ей, и, если это не случайность, следует серьезно задуматься: всегда ли верна теория (а иногда и о том, верна ли она вообще).
Несмотря на большое число экспериментов, свидетельствовавших в пользу теории Бора, ряд фактов она объяснить не смогла (например, интенсивность спектральных линий, количественный расчет атома гелия, дублетные линии в спектрах и многое другое). В чем же причина? Очевидно, во внутренней противоречивости теории и в попытках соединить несоединимое — классику и квантовые постулаты, и не только в предельных случаях, а во всей области действия.
В 1926-1927 годах Э.Шрёдингер и В.Гейзенберг, опираясь на теорию Бора и многочисленные экспериментальные и теоретические посылки, заложили фундамент последовательной теории строения атома — квантовой механики. А что же теория Бора? Ряд ее результатов, например правила квантования Бора — Зоммерфельда, стали тем предельным случаем, в котором квантовая механика пересеклась с теорией Бора. Некоторые результаты представляют огромный исторический интерес, а идея дискретности микромира — важнейший отправной пункт дальнейших исследований ученых. Теория Бора, по словам Эйнштейна, была «наивысшей музыкальностью в области мысли». Высокую оценку трудов ученого дал и Резерфорд: «Я рассматриваю труды Бора как величайший триумф человеческой мысли».
В 1922 году Бор получил Нобелевскую премию по физике «За заслуги в изучении строения атома».
В
начале ХХ века уже было известно, что в
состав атома входят электроны. Поскольку
атом электрически нейтрален, а электрон
имеет отрицательный заряд, то было
очевидным, что в состав атома входит и
положительный заряд. Масса атома
значительно превышала массу его
электронов. Резерфорд поставил задачу
опытным путём изучить распределение
положительного заряда внутри атома.
В своём опыте он
подверг бомбардировке альфа-частицами
тонкую золотую фольгу. Альфа-частицы
имели положительный заряд, а их масса
почти в 2000 раз превышала массу электрона.
Золотая фольга была очень тонкой толщиной
10–6
м, но по атомным меркам её толщина
составляла около 10000 атомных слоёв.
Ожидалось, что золотая фольга станет
серьёзной преградой на пути альфа-частиц,
но оказалось напротив. Основной поток
альфа-частиц свободно пролетал сквозь
преграду. Из этого вытекало, что атом
внутри практически пустой, т.е.
положительный заряд занимает очень
малый объём атома. Однако отдельные
альфа-частицы (очень малая часть)
отклонились на значительные углы от
первоначального направления. Из этого
вытекало, что с маленьким положительным
ядром атома связана практически вся
его масса.
На основании
результатов опыта Резерфорд предложил
следующую модель атома. В
центре атома расположено положительное
массивное ядро, вокруг которого вращаются
электроны как планеты вокруг Солнца.
Из опыта оценили размер ядра как 10–14
м, когда
размер атома, полученный ранее, составлял
порядка 10–10м.
Электроны на орбитах атома удерживала
сила кулоновского притяжения, действующая
между разноимёнными зарядами.
Постулаты бора
Планетарная модель
атома была наилучшей из всех предложенных,
однако имела существенные противоречия.
При движении заряженной частицы с
ускорением должна излучаться
электромагнитная волна. В модели атома
электроны имеют центростремительное
ускорение, однако при этом атом не
излучает волны. Более того, при излучении
волны атом должен терять энергию, радиус
орбиты должен уменьшаться и электрон
должен упасть на ядро. Возникали
непреодолимые противоречия, из которых
уже следовало, что классический подход
к описанию атома не совсем подходит или
совсем не подходит.
Для того чтобы
пассивно не ждать, когда будет придумана
новая теория, а конструктивно работать
с планетарной моделью атома Бор предложил
принять три постулата. Постулаты это
некоторые утверждения, заложенные в
основу новой теории. Они могут обсуждаться
или доказываться, но не в рамках этой
новой теории.
Первый
постулат.
Существуют
стационарные состояния атома, находясь
в которых, он не излучает энергии.
Второй
постулат. В
стационарном состоянии атома электрон,
двигаясь по круговой орбите, имеет
квантованные (дискретные) значения
момента импульса, которые
удовлетворяют условию
(1)
где
L
= mr
момент импульса электрона; m
и
— его масса и скорость; r
— радиус его орбиты; n
= 1, 2, 3,…, h
постоянная Планка.
Третий
постулат. Испускание
(или поглощение) света атомом происходит
только тогда, когда электрон переходит
из одного стационарного состояния в
другое. При этом испускается (или
поглощается) один световой фотон, энергия
которого определяется
соотношением
h
= Wn
Wi,
(2)
где
Wn
и Wi
энергия верхнего и нижнего состояния
соответственно. Если происходит переход
из состояния с меньшей энергией в
состояние с большей энергией, то
наблюдается поглощение энергии (света).
Испускание наблюдается при уменьшении
энергии атома, а поглощение при увеличении.
Отсюда
(3)
Соседние файлы в папке ЛЕКЦИИ ЭКОНОМ
- #
- #
- #
- #
- #
- #
- #
- #
- #