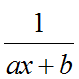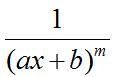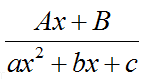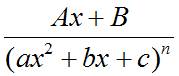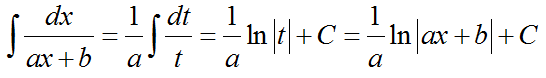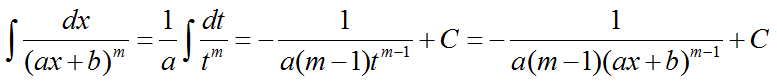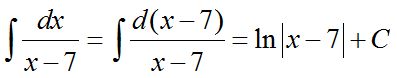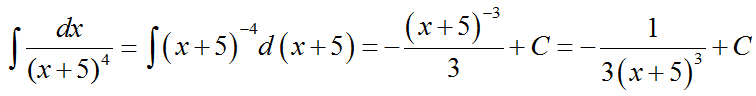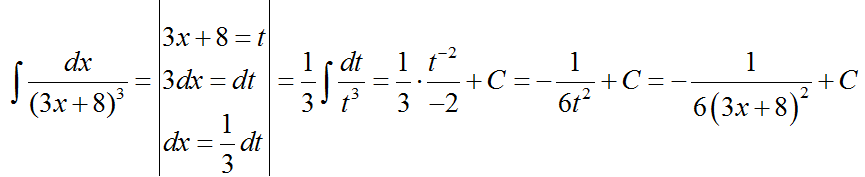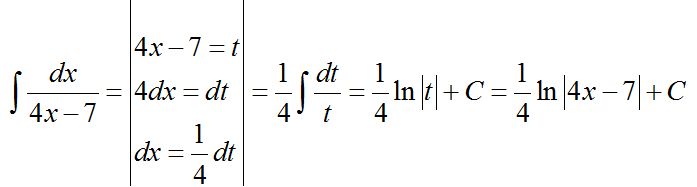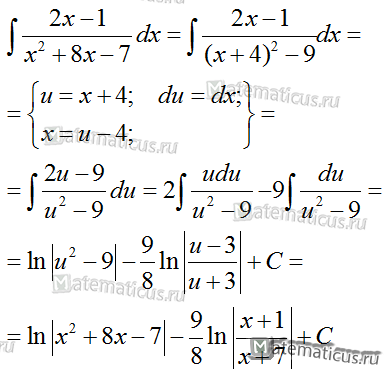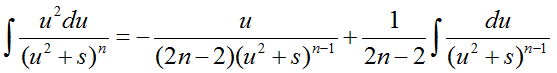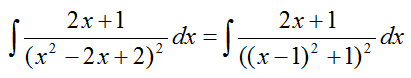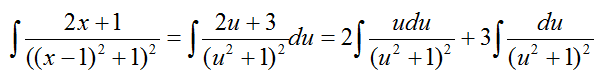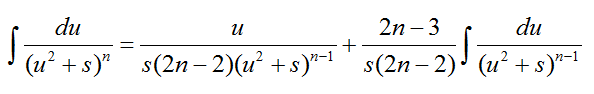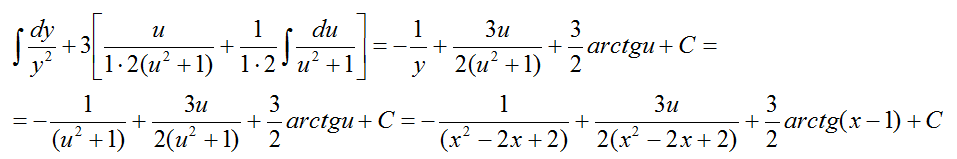Задача
нахождения неопределенного интеграла
дробно рациональной функции сводится
к интегрированию простейших дробей.
Поэтому рекомендуем для начала
ознакомиться с разделом теории разложение
дроби на простейшие.
Пример.
Найти
неопределенный интеграл .
Решение.
Так
как степень числителя подынтегральной
функции равна степени знаменателя, то
для начала выделяем целую часть,
проводя деление
столбиком многочлена на многочлен:
Поэтому, 
Разложение
полученной правильной рациональной
дроби на
простейшие дроби имеет вид.
Следовательно,
Полученный
интеграл представляет собой интеграл
простейшей дроби третьего типа. Забегая
немного вперед, отметим, что взять его
можно методом подведения
под знак дифференциала.
Так
как ,
то.
Поэтому
Следовательно,
Теперь
перейдем к описанию методов интегрирования
простейших дробей каждого из четырех
типов.
Интегрирование
простейших дробей первого типа
Для
решения этой задачи идеально подходит метод
непосредственного интегрирования:
Пример.
Найти
множество первообразных функции
Решение.
Найдем
неопределенный интеграл ,
используя свойства первообразной,
таблицу первообразных и правило
интегрирования.
К
началу страницы
Интегрирование
простейших дробей второго типа
Для
решения этой задачи также подходит
метод непосредственного интегрирования:
Пример.
Найдите
неопределенный интеграл 
Решение.
К
началу страницы
Интегрирование
простейших дробей третьего типа
Для
начала представляем неопределенный
интеграл 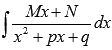
виде суммы:
Первый
интеграл берем методом подведения под
знак дифференциала:
Поэтому,
У
полученного интеграла преобразуем
знаменатель:
Следовательно,
Формула
интегрирования простейших дробей
третьего типа принимает вид:
Пример.
Найдите
неопределенный интеграл .
Решение.
Используем
полученную формулу:
Если
бы у нас не было этой формулы, то как бы
мы поступили:
9. Интегрирование простейших дробей четвертого типа
Первый
шаг – подводим под знак дифференциала:
Второй
шаг – нахождение интеграла вида 
Интегралы подобного вида находятся с
использованием рекуррентных формул.
(Смотрите разделинтегрирование
с использованием рекуррентных формул).
Для нашего случая подходит следующая
рекуррентная формула:
Пример.
Найдите
неопределенный интеграл
Решение.
Для
данного вида подынтегральной функции
используем метод подстановки. Введем
новую переменную (смотрите
раздел интегрирование
иррациональных функций):
После
подстановки имеем:
Пришли
к нахождению интеграла дроби четвертого
типа. В нашем случае имеем коэффициенты М
= 0, р = 0, q = 1, N = 1 и n
= 3.
Применяем рекуррентную формулу:
После
обратной замены получаем
результат:
10. Интегрирование тригонометрических функций.
Множество
задач сводится к нахождению интегралов
трансцендентных функций, содержащих
тригонометрические функции. В данной
статье сгруппируем наиболее часто
встречающиеся виды подынтегральных
функций и на примерах рассмотрим методы
их интегрирования.
-
Начнем
с интегрирования синуса, косинуса,
тангенса и котангенса.
Из
таблицы первообразных сразу заметим,
что и
.
Метод
подведения под знак дифференциалапозволяет
вычислить неопределенные интегралы
функций тангенса и котангенса:
К
началу страницы
-
Поясним,
как были найдены формулыи
,
находящиеся в таблице первообразных.
Разберем
первый случай, второй абсолютно
аналогичен.
Воспользуемся методом
подстановки:
Пришли
к задаче интегрирования
иррациональной функции. Здесь нам
также поможет метод подстановки:
Осталось
провести обратную замену иt
= sinx:
К
началу страницы
-
Отдельно
хочется остановиться на интегралах,
содержащих степени тригонометрических
функций, вида.
Подробно
о принципах их нахождении можете
ознакомиться в разделеинтегрирование
с использованием рекуррентных формул.
Если изучите вывод этих формул, то без
особого труда сможете брать интегралы
вида,
гдеm и n –
натуральные числа.
К
началу страницы
-
Когда
тригонометрические функции идут в
комбинациях с многочленами или
показательными функциями, то
применяется метод
интегрирования по частям. В этом
разделе даны рекомендации для нахождения
интегралов,
.
К
началу страницы
-
Максимум
творчества приходится вкладывать,
когда подынтегральная функция содержит
тригонометрические функции с различными
аргументами.
Здесь
на помощь приходят основные формулы
тригонометрии. Так что выписывайте их
на отдельный листочек и держите перед
глазами.
Пример.
Найти
множество первообразных функции 
Решение.
Формулы
понижения степени дают и
.
Поэтому
Знаменатель
представляет собой формулу синуса
суммы, следовательно,
Приходим
к сумме трех интегралов.
К
началу страницы
-
Подынтегральные
выражения, содержащие тригонометрические
функции, иногда можно свести к дробно
рациональным выражениям, используя
стандартную тригонометрическую
подстановку.
Выпишем
тригонометрические формулы, выражающие
синус, косинус, тангенс через тангенс
половинного аргумента:
При
интегрировании нам также понадобится
выражение дифференциала dx через
тангенс половинного угла.
Так
как 
то
То
есть, ,
где.
Пример.
Найти
неопределенный интеграл .
Решение.
Применим
стандартную тригонометрическую
подстановку:
Таким
образом, .
Разложение
на простейшие дробиподынтегральной
функции приводит нас к сумме двух
интегралов:
Осталось
провести обратную замену :
11.
Рекуррентные формулы – это формулы,
выражающие n-ый
член последовательности через предыдущие
члены. При нахождении интегралов они
не редко используются.
Мы
не ставим целью перечислить все
рекуррентные формулы, а хотим дать
принцип их получения. Вывод этих формул
основан на преобразовании подынтегральной
функции и применении метода
интегрирования по частям.
К
примеру, неопределенный интеграл можно
взять, используя рекуррентную формулу.
Вывод
формулы 
Используя
формулы тригонометрии, можно записать:
Полученный
интеграл найдем методом интегрирования
по частям. В качестве функции u(x)возьмем cosx,
следовательно, .
Поэтому,
Возвращаемся
к исходному интегралу:
То
есть,
Что
и требовалось показать.
Аналогично
выводятся следующие рекуррентные
формулы:
-
Для
нахождения интегралов видаиспользуется
рекуррентная формула,n –
натуральное число. -
Для
нахождения интегралов видаиспользуется
рекуррентная формула.
-
Для
нахождения интегралов видаиспользуется
рекуррентная формула.
-
Для
нахождения интегралов видаиспользуется
рекуррентная формула.
Пример.
Найти
неопределенный интеграл .
Решение.
Используем
рекуррентную формулу из четвертого
пункта (в нашем примере n
= 3):
Так
как из таблицы первообразных имеем ,
то
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интегрирование рациональных дробей
Рациональной дробью называется дробь вида
– многочлены степени m и n соответственно. Рациональная дробь называется правильной , если степень числителя меньше степени знаменателя (m Пример 1
Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.
Алгоритм интегрирования рациональной дроби
1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:

3. Представим дробь
виде суммы простейших дробей с неопределенными коэффициентами.
- Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.
- Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях x.
- Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая равным действительным корням знаменателя.
- Подставим найденные коэффициенты A1,A2,…,Cs,Ds в разложение дроби.
- Проинтегрируем простейшие дроби.
Примеры интегрирования рациональных функций
Пример 4.
Корни знаменателя: x=1, а x 2 +1 = 0 не имеет действительных корней.
Тогда разложение для данной дроби имеет вид:
Приводя полученные дроби к общему знаменателю, получим тождество:
Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.
Подставим найденные коэффициенты в разложение и проинтегрируем дроби.
Интегрирование рациональных функций и метод неопределённых коэффициентов
Алгоритм интегрирования рациональных функций
Рациональная функция — это дробь вида , числитель и знаменатель которой — многочлены или произведения многочленов.
Из урока «Интегрирование некоторых рациональных дробей и иррациональностей» известно, что рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе. В том же уроке говорилось о том, как представить неправильную дробь в виде суммы её целой части и некоторой правильной дроби.
На этом уроке будем учиться интегрировать такие рациональные функции, которые представлены в виде правильных дробей. Для этого существует метод неопределённых коэффициентов, основанный на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.
Приведённый ниже алгоритм интегирования рациональных функций будет пошагово проиллюстрирован в примерах.
Алгоритм интегрирования рациональных функций
- Шаг 1. Определить вид многочлена в знаменателе дроби (он может иметь действительные, кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить дробь на простые дроби, в числителях которых — неопределённые коэффициенты, число которых равно степени знаменателя.
- Шаг 2. Определить значения неопределённых коэффициентов. Для этого потребуется решить систему уравнений, сводящуюся к системе линейных уравнений.
- Шаг 3. Найти интеграл исходной рациональной функции (дроби) как сумму интегралов полученных простых дробей, к которым применяются табличные интегралы.
Переходим к первому шагу алгоритма
Шаг 1: разложение исходной дроби
Многочлен в знаменателе имеет действительные корни. То есть, в знаменателе имеет место цепочка сомножителей вида , в которой каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
Пример 1. Шаг 1. Дан интеграл от рациональной функции .
От нас требуется разложить подынтегральное выражение — правильную дробь на простые дроби.
Решение. Дискриминант уравнения положительный, поэтому многочлен в знаменателе имеет действительные корни. Получаем следующее разложение исходной дроби на сумму простых дробей:
.
Пример 2. Шаг 1.Дан интеграл от рациональной функции
.
Решение. Разложим знаменатель подынтегрального выражения на множители. Сначала можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь:
.
Для разложения квадратного трёхчлена в скобках решаем квадратное уравнение:
Получаем разложение знаменателя на множители в подынтегральном выражении:
.
Дискриминант решённого выше квадратного уравнения положительный, то есть имеем дело со случаем, когда многочлен в знаменателе имеет действительные корни. Разложение исходной дроби подынтегрального выражения будет следующим:
.
Как и в первом примере, числа, обозначенные большими буквами, пока неизвестны. Отсюда и название — метод неопределённых коэффициентов.
Многочлен в знаменателе имеет кратные действительные корни. Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида , то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
Пример 3. Шаг 1. Дан интеграл от рациональной функции .
Решение. Представляем разность квадратов в виде произведения суммы и разности .
Тогда подынтегральное выражение запишется в виде
,
все уравнения с многочленами которого имеют действительные корни. Это случай кратных действительных корней, так как последний сомножитель находится во второй степени. Получаем следующее разложение исходной дроби на простые дроби:
Как видим, в этом случае нужно понижать степень кратного многочлена с исходной до первой и записывать простую дробь с каждой из этих степеней в знаменатель.
Пример 4. Шаг 1. Дан интеграл от рациональной функции .
Решение. Уравнения с многочленами в знаменателе имеют действительные корни, а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее разложение исходной дроби на простые дроби:
.
Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля. В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в числителе нужно записывать линейное выражение с переменной x (это выражение — последнее в следующей записи):
Пример 5. Шаг 1. Дан интеграл от рациональной функции .
Решение. Уравнение в скобках имеет комплексные корни, а оба сомножителя присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:
.
Пример 6. Шаг 1. Дан интеграл от рациональной функции .
Решение. Представим знаменатель дроби в подынтегральном выражении в виде следующего произведения сомножителей:
.
Решение. Уравнение с последним сомножителем имеет комплексные корни, а все сомножители присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:
Многочлен в знаменателе имеет кратные комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
То есть в сумме простых дробей число простых дробей с линейным выражением в числителе должно быть равно степени сомножителя, имеющего комплексные корни.
Пример 7. Шаг 1. Дан интеграл от рациональной функции .
Решение. Квадратный трёхчлен имеет комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
.
Пример 8. Шаг 1. Дан интеграл от рациональной функции .
Решение. Квадратный трёхчлен в знаменателе имеет комплексные корни и присутствует в подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:
.
Шаг 2: нахождение неопределённых коэффициентов
На первом шаге мы представили подынтегральные дроби в виде суммы дробей с неопределёнными коэффициентами. В начале этого шага потребуется привести полученную сумму дробей к общему знаменателю. После этого в их числителях будут произведения неопределённых коэффициентов на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях.
Полученное таким образом выражение приравнивается к числителю исходной дроби. Затем составляется система из уравнений, в которых степени икса одинаковы. Путём решения системы и находятся неопределённые коэффициенты. Для решения достаточно знать, как системы уравнений решаются методом подстановки и методом сложения.
Пример 1. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:
.
Раскрываем скобки и приравниваем полученое к полученному выражению числитель исходной подынтегральной дроби:
.
В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:
.
Сокращаем все иксы и получаем эквивалентную систему уравнений:
.
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:
Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:
Решаем полученную систему:
Итак, , отсюда получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:
Как и в предыдущих примерах составляем систему уравнений:
Сокращаем иксы и получаем эквивалентную систему уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
После известных действий с полученной суммой должна получиться следующая система уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:
.
Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем:
Можно заметить, что если принять за значение икса единицу, то второе и третье слагаемые в правой части равенства обратятся в нули и нет необходимости их вычислять. Тогда получаем, что . Далее по уже отработанной схеме получаем систему уравнений:
Решая систему, получаем следующие значения неопределённых коэффициентов:
.
Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Шаг 3: нахождение интеграла исходной функции (дроби)
Полученные простые дроби и интегировать проще. К исходной сумме дробей применяется правило интеграла суммы (интеграл суммы равен сумме интегралов) и табличные интегралы. Чаще всего требуется применять табличные интегралы, приводящие к натуральному логарифму и арктангенсу.
Пример 1. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Интегрируем изначальную рациональную функцию как сумму дробей и используем табличный интеграл 10, приводящий к натуральному логарифму:
Последнее действие с натуральным логарифмом — приведение к единому выражению под логарифмом — может требоваться при выполнении работ, но требуется не всегда.
Пример 2. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Вновь применяем табличный интеграл, приводящий к натуральному логарифму:
Пример 3. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
.
В результате интегрирования получаем сумму натуральных логарифмов и одной простой дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:
Пример 4. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
В результате интегрирования получаем сумму натуральных логарифмов и одной дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:
Пример 5. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Интегрируем и получаем сумму натурального логарифма и арктангенса:
Пример 6. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Опять получаем сумму натурального логарифма и арктангенса:
Пример 7. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Интегрируя, получаем натуральные логарифмы и дробь:
Приведение к единому логарифму попробуйте выполнить самостоятельно.
Пример 8. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:
.
Интегрируя, получаем сумму натурального логарифма, арктангенса и дроби:
Примеры интегрирования рациональных функций (дробей)
Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей:
, , .
Пример 1
Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя ( 3 ) меньше степени многочлена числителя ( 4 ). Поэтому, вначале необходимо выделить целую часть дроби.
1. Выделим целую часть дроби. Делим x 4 на x 3 – 6 x 2 + 11 x – 6 :
Отсюда
.
2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, 3, 6, –1, –2, –3, –6 .
Подставим x = 1 :
.
Итак, мы нашли один корень x = 1 . Делим на x – 1 :
Отсюда
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.
3. Разложим дробь на простейшие.
.
Итак, мы нашли:
.
Интегрируем.
Пример 2
Здесь в числителе дроби – многочлен нулевой степени ( 1 = x 0 ). В знаменателе – многочлен третьей степени. Поскольку 0 , то дробь правильная. Разложим ее на простейшие дроби.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x ). То есть целый корень может быть одним из чисел:
1, 3, –1, –3 .
Подставим x = 1 :
.
Итак, мы нашли один корень x = 1 . Делим x 3 + 2 x – 3 на x – 1 :
Итак,
.
Решаем квадратное уравнение:
x 2 + x + 3 = 0 .
Находим дискриминант: D = 1 2 – 4·3 = –11 . Поскольку D 0 , то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на ( x – 1)( x 2 + x + 3) :
(2.1) .
Подставим x = 1 . Тогда x – 1 = 0 ,
.
Подставим в (2.1) x = 0 :
1 = 3 A – C ;
.
Приравняем в (2.1) коэффициенты при x 2 :
;
0 = A + B ;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.
Вычисляем I 2 .
.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0 . Поэтому знак модуля можно опустить.
Пример 3
Здесь под знаком интеграла стоит дробь из многочленов. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3 . Степень многочлена знаменателя дроби равна 4 . Поскольку 3 , то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, –1, –2 .
Подставим x = –1 :
.
Итак, мы нашли один корень x = –1 . Делим на x – (–1) = x + 1 :
Итак,
.
Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, –1, –2 .
Подставим x = –1 :
.
Итак, мы нашли еще один корень x = –1 . Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.
Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на ( x + 1) 2 ( x 2 + 2) :
(3.1) .
Подставим x = –1 . Тогда x + 1 = 0 ,
.
Продифференцируем (3.1):
;
.
Подставим x = –1 и учтем, что x + 1 = 0 :
;
; .
Подставим в (3.1) x = 0 :
0 = 2 A + 2 B + D ;
.
Приравняем в (3.1) коэффициенты при x 3 :
;
1 = B + C ;
.
Итак, мы нашли разложение на простейшие дроби:
.
Автор: Олег Одинцов . Опубликовано: 10-05-2015
http://function-x.ru/integral201.html
http://1cov-edu.ru/mat_analiz/integrali/neopredelennie/ratsionalnye/primery/
Простыми или элементарными называются дроби, следующих типов (всего их 4 типа):
где m, n – натуральные числа и m≥2, n≥2, D=b2 – 4ac<0.
Интегрирование простых дробей 1-ого и 2-ого типов.
Формула для интегрирования дробей первого типа:
Формула для интегрирования дробей второго типа:
Решения первого и второго типов интегралов просты. Преобразуются к табличному виду за счёт подстановки t = ax + b.
Рассмотрим примеры решений интегралов простых дробей первого и второго типов.
1.
2.
3.
4.
Интегрирование простых дробей 3-ого типа.
Общее решение уравнения третьего типа можно представить формулой:
Рассмотрим пример интегрирование простой дроби третьего типа
Интегрирование простых дробей 4-ого типа.
Общее решение такого уравнения можно представить формулой:
Здесь первый интеграл находим с помощью подстановки — t = u2 +s и преобразовываем к табличному виду $int {frac{{dt}}{{{t^n}}}} $, второй — используя рекуррентную формулу и метод интегрирования по частям:
Рассмотрим пример интегрирование простой дроби четвертого типа:
Пример
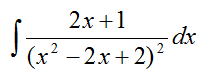
Решение
Пусть u=x-1, тогда x=u-1 и du=dx, получаем
Сделаем подстановку для правого выражения.
Пусть y=u2+1, тогда dy=2udu и воспользуемся формулой
имеем
1. Интегрирование рациональных дробей.
2. Алгоритм интегрирования рациональной дроби.
3. Примеры интегрирования рациональных функций.
Интегрирование рациональных дробей
Рациональной дробью называется дробь вида
– многочлены степени m и n соответственно. Рациональная дробь называется правильной , если степень числителя меньше степени знаменателя (m<n), в противном случае дробь называется неправильной .
Простейшими элементарными дробями называются дроби следующего вида:
Пример 1
Пример 2
Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.
Пример 3.
Алгоритм интегрирования рациональной дроби
1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:

3. Представим дробь
виде суммы простейших дробей с неопределенными коэффициентами.
- Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.
- Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях x.
- Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая равным действительным корням знаменателя.
- Подставим найденные коэффициенты A1,A2,…,Cs,Ds в разложение дроби.
- Проинтегрируем простейшие дроби.
Примеры интегрирования рациональных функций
Пример 4.
Корни знаменателя: x=1, а x2+1 = 0 не имеет действительных корней.
Тогда разложение для данной дроби имеет вид:
Приводя полученные дроби к общему знаменателю, получим тождество:
Пример 5.
Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.
Подставим найденные коэффициенты в разложение и проинтегрируем дроби.
Интегрирование простейших рациональных дробей
Напомним, что дробно-рациональными называют функции вида
$$
f(x) = frac{P_n(x)}{Q_m(x)},
$$
в общем случае являющиеся отношением двух многочленов %%P_n(x)%% и %%Q_m(x)%%.
Если %%m > n geq 0%%, то рациональную дробь называют правильной, в противном случае — неправильной. Используя правило деления многочленов, неправильную рациональную дробь можно представить в виде суммы многочлена %%P_{n — m}%% степени %%n — m%% и некоторой правильной дроби, т.е.
$$
frac{P_n(x)}{Q_m(x)} = P_{n-m}(x) + frac{P_l(x)}{Q_n(x)},
$$
где степень %%l%% многочлена %%P_l(x)%% меньше степени %%n%% многочлена %%Q_n(x)%%.
Таким образом, неопределенный интеграл от рациональной функции можно представить суммой неопределенных интегралов от многочлена и от правильной рациональной дроби.
Интегралы от простейших рациональных дробей
Среди правильных рациональных дробей выделяют четыре типа, которые относят к простейшим рациональным дробям:
- %%displaystyle frac{A}{x — a}%%,
- %%displaystyle frac{A}{(x — a)^k}%%,
- %%displaystyle frac{Ax + B}{x^2 + px + q}%%,
- %%displaystyle frac{Ax + B}{(x^2 + px + q)^k}%%,
где %%k > 1%% — целое и %%p^2 — 4q < 0%%, т.е. квадратные уравнения не имеют действительных корней.
Вычисление неопределенных интегралов от дробей первых двух типов
Вычисление неопределенных интегралов от дробей первых двух типов не вызывает затруднений:
$$
begin{array}{ll}
int frac{A}{x — a} mathrm{d}x &= Aint frac{mathrm{d}(x — a)}{x — a} = A ln |x — a| + C, \
\
int frac{A}{(x — a)^k} mathrm{d}x &= Aint frac{mathrm{d}(x — a)}{(x — a)^k} = A frac{(x-a)^{-k + 1}}{-k + 1} + C = \
&= -frac{A}{(k-1)(x-a)^{k-1}} + C.
end{array}
$$
Вычисление неопределенного интегралов от дробей третьего типа
Дробь третьего типа сначала преобразуем, выделив полный квадрат в знаменателе:
$$
frac{Ax + B}{x^2 + px + q} = frac{Ax + B}{(x + p/2)^2 + q — p^2/4},
$$
так как %%p^2 — 4q < 0%%, то %%q — p^2/4 > 0%%, которое обозначим как %%a^2%%. Заменив также %%t = x + p/2, mathrm{d}t = mathrm{d}x%%, преобразуем знаменатель и запишем интеграл от дроби третьего типа в форме
$$
begin{array}{ll}
int frac{Ax + B}{x^2 + px + q} mathrm{d}x &= int frac{Ax + B}{(x + p/2)^2 + q — p^2/4} mathrm{d}x = \
&= int frac{A(t — p/2) + B}{t^2 + a^2} mathrm{d}t = int frac{At + (B — A p/2)}{t^2 + a^2} mathrm{d}t.
end{array}
$$
Последний интеграл, используя линейность неопределенного интеграла, представим в виде суммы двух и в первом из них введем %%t%% под знак дифференциала:
$$
begin{array}{ll}
int frac{At + (B — A p/2)}{t^2 + a^2} mathrm{d}t &= Aint frac{t mathrm{d}t}{t^2 + a^2} + left(B — frac{pA}{2}right)int frac{mathrm{d}t}{t^2 + a^2} = \
&= frac{A}{2} int frac{mathrm{d}left(t^2 + a^2right)}{t^2 + a^2} + — frac{2B — pA}{2}int frac{mathrm{d}t}{t^2 + a^2} = \
&= frac{A}{2} ln left| t^2 + a^2right| + frac{2B — pA}{2a} text{arctg}frac{t}{a} + C.
end{array}
$$
Возвращаясь к исходной переменной %%x%%, в итоге для дроби третьего типа получаем
$$
int frac{Ax + B}{x^2 + px + q} mathrm{d}x = frac{A}{2} ln left| x^2 + px + qright| + frac{2B — pA}{2a} text{arctg}frac{x + p/2}{a} + C,
$$
где %%a^2 = q — p^2 / 4 > 0%%.
Вычисление интеграла 4 типа сложно, поэтому в этом курсе не рассматривается.


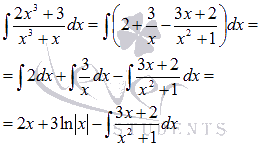























 и
и ,
,

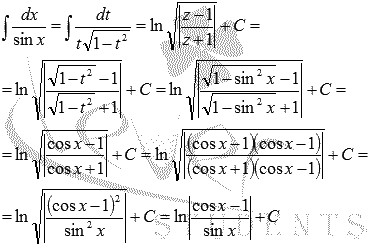

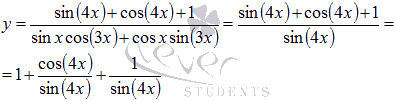






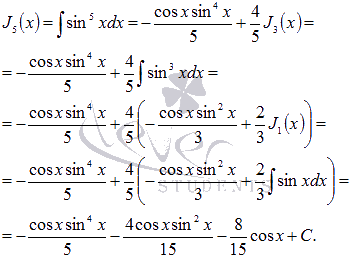





 используется
используется