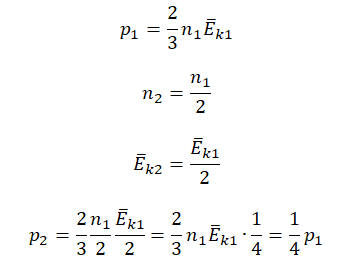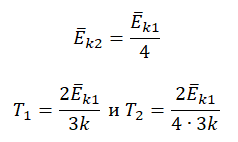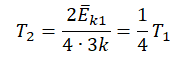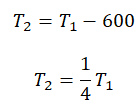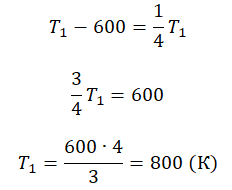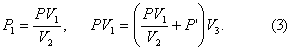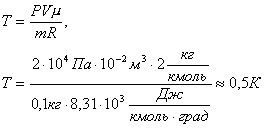Как найти первоначальное давление газа в физике

Определение

Идеальный газ — газ, удовлетворяющий трем условиям:

Молекулы — материальные точки.
Потенциальная энергия взаимодействия молекул пренебрежительно мала.
Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 ^oC).
По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

∆t = ∆T

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

T = t + 273

Если особо важна точность, следует использовать более точную формулу:

T = t + 273,15

Пример №1. Температура воды равна ^oC. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p=23n−Ek

p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p=13m0n−v2

m0— масса одной молекулы газа;

n — концентрация молекул газа;

−v2 — среднее значение квадрата скорости молекул газа.

Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости:

v=√−v2

p=13ρ−v2

ρ — плотность газа

p=nkT

k — постоянная Больцмана (k = 1,38∙10^–3 Дж/кг)

T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v=√3kTm0=√3RTM

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R=NAk=8,31 Дж/К·моль

Температура — мера кинетической энергии молекул идеального газа:

−Ek=32kT

T=2−Ek3k

Полная энергия поступательного движения молекул газа определяется формулой:

E=N−Ek

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Следовательно:

Составим систему уравнений:

Отсюда:

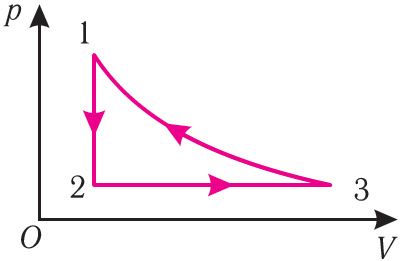
Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

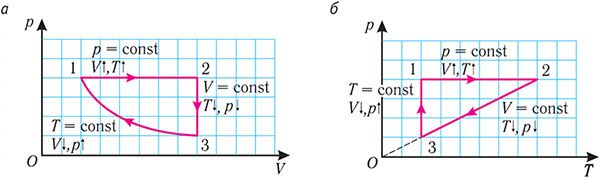
График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1=p2V2T2

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17560

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Ответ:

а) 13p1

б) 2p1

в) 23p1

г) 43p1

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для состояний 1 и 2.

4.Выразить искомую величину.

Решение

Исходные данные:

• Начальное давление: p₀.

• Начальная концентрация молекул: n₁ = 3n.

• Конечная концентрация молекул: n₂ = n.

• Начальная средняя энергия хаотичного движения молекул: E_k1 = E_k.

• Конечная средняя энергия хаотичного движения молекул: E_k2 = 2E_k.

Основное уравнение МКТ:

p=23n−Ek

Составим уравнения для начального и конечного состояний:

p1=23n1−Ek1=233n−Ek=2n−Ek

p2=23n2−Ek2=23n2−Ek=43n−Ek

Отсюда:

n−Ek=p12=3p24

p2=4p16=23p1

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18416

Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Концентрации кислорода и водорода в сосуде равны. Следовательно, n₁ = n₂ = n.

• Давление кислорода вдвое выше давления водорода. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n−Ek1

p2=23n2−Ek2 или p=23n−Ek2

Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:

−Ek1=3pn

−Ek2=3p2n

Поделим уравнения друг на друга и получим:

−Ek1−Ek2=3pn·2n3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18824

В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение концентрации молекул аргона к концентрации молекул неона.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.

• Давление аргона в 2 раза больше давления неона. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n1−Ek

p2=23n2−Ek2 или p=23n2−Ek

Выразим концентрации молекул газа из каждого уравнения:

n1=3p−Ek

n2=3p2−Ek

Поделим уравнения друг на друга и получим:

n1n2=3p−Ek·2−Ek3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 10.9k

Источник

Решебник по физике за 10, 11 класс (А.П. Рымкевич, 2001 год),
задача №511
к главе «25. Изопроцессы».

1 Если нет специальных оговорок, то при решении задач этого параграфа можно атмосферное давление принимать равным 100 кПа. В задачах 514—526 процесс считать изотермическим, в задачах 527—533 — изобарным и в задачах 534—540 — изохорным.

V₂ = 5 л, ΔP = 60 кПа. Найти: P.

Ответ

Проверено экспертом

Пусть газ находится в плотном сосуде, тогда его объем не меняется

раз объем не меняется (также допускаем, что масса тоже неизменна), то справедлив закон Шарля:

P0 / T0 = (P0 + 2*10^(4)) / T,

P0 T = T0 (P0 + 2*10^(4)).

дальше, в теории, можно выразить P0, но, как по мне, проще решить линейное уравнение:

Решение отдельных задач

Задача 1. При сжатии газа его объем уменьшился на 2 л, а давление увеличилось в 2 раза. Найти первоначальный объем газа V ₁ .

Обозначим Δ V изменение объема газа, P ₁ и P ₂ – давления газа до и после сжатия.

Решение. Судя по условию задачи, здесь процесс изотермический. Правда следовало бы добавить, что процесс сжатия происходит медленно, потому что, если бы он происходил быстро, то это был уже адиабатный процесс, при котором температура газа тоже меняется. Но, как правило, при условии задач на газовые процессы об этом упомянуть забывают, поэтому мы и обратили на этот момент внимание.

Произведем вычисления V ₁= 2·2л=4л

Задача 2. В узкой откачанной и запаянной с двух концов горизонтальной трубке посредине находится столбик ртути длиной 0,3 м. Если трубку поставить вертикально, столбик ртути сместится на 15 см. Определить давление в трубке до того как из нее откачали воздух, если ее длина 1м, а плотность ртути13,6·10 3 кг/м 3 .

Решение. По условию задачи температура газа остается постоянной, поэтому при решении задачи можно применить закон Бойля-Мариотта. Состояние воздуха в трубке в горизонтальном положении определялось параметрами: объемом V ₁ и давлением P . Выразим объем через поперечное сечение трубки S и высоту воздушного столбика , то есть

При вертикальном положении трубки состояние газа в верхней части трубки определялось параметрами: объемом и давлением P ₁. В нижней части трубки объем стал и давление P ₂= P ’+ P ₁. Столбик ртути находился в равновесии, когда давление воздуха в нижней части трубки равно сумме давления воздуха в верхней части трубки и давление столбика ртути P ’= ρgh .

Запишем закон Бойля-Мариотта для состояния газа в верхней части трубки

и для нижней части трубки

Выражение P ₁, полученное из (1), подставим в (2)

В равенство (3) подставим значения

Задача 3. Газ массой 12·10 -3 кг занимает объем 6·10 -3 м 3 при температуре 180 0 С. При какой температуре плотность этого газа будет равна 6 кг/м 3 .

Решение: Плотность газа при постоянном давлении и массе обратно пропорциональна объему, то есть

но при постоянном давлении объем прямо пропорционален абсолютной температуре 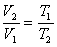тогда . Отсюда , но , окончательно получим

Задача 4. Определить на сколько изменилась масса гелия, находящегося в баллоне объемом 0,25 м 3 под давлением 10 6 Па при температуре 20 0 С, если из баллона была выпущена часть массы газа, после чего давление понизилось до 10 5 Па, а температура уменьшилась до 10 0 С.

Решение. До того как часть газа была выпущена из баллона его состояние определялось такими параметрами: давление Р₁, объем V _, масса m ₁, температура Т₁. После того как часть газа была выпущена из баллона, состояние газа стало определяться параметрами: Р₂, V , m ₂, T ₂.Запишем уравнение Менделеева-Клапейрона для первого и второго состояния газа

где V – объем газа, который по условию задачи остается неизменным; μ – молекулярный вес гелия. Выразим из этих уравнений m ₁ и m ₂ и найдем их разность Δ m

Задача 5. Определить объем баллона со сжатым углекислым газом, находящимся под давлением в 100 атмосфер при температуре 27 0 С, если при нормальных условиях то же количество углекислого газа занимает объем 1,3 м 3 .

Решение. При нормальных условиях состояние газа определяется параметрами: Т, P , V . При данных условиях – параметрами Т, P , V . Так как масса газа не изменялась, то для решения задачи можно воспользоваться уравнением объединенного газового закона:

Задача 6. При какой температуре находилось 100 г водорода в баллоне объемом 10 л, если давление при этом было 2 . 10 4 Па?

m=100 г=0,1кг
μ=2 кг/кмоль
V =10л=10 -2 м 3
P =2·10 4 Па
R =8,3·10 3 Дж/кмоль·град

Решение. Из уравнения Менделеева-Клапейрона PV = m /_µ· RT находим температуру:

Задача 7. Определить плотность азота при температуре 27 0 С и давлении 760 мм рт. ст.

t =27 0 C
T =300К
P =760мм рт. ст. » 10 5 Па
μ=28 кг/кмоль
R =8,3·10 3 Дж/кмоль·град

Решение. Из уравнения Менделеева-Клапейрона найдем плотность азота PV = m /_µ· RT откуда

Задача 8. Определить по графику зависимость объема от температуры. Характер изменения давления, под которым находился газ во время нагревания, показан на рисунке (а).

Решение. Для решения задачи необходимо из начала координат провести изобары, на которых лежат точки 1 и 2 (см. рисунок (б)). Точка 1 лежит на изобаре, которая составляет с осью абсцисс меньший угол, чем изобара, проходящая через точку 2. Из уравнения газового состояния следует, что тангенс угла наклона изобары пропорционален 1/ P . Тогда из рисунка видим, что давление газа убывает при переходе из состояния 1 в состояние 2. Нагревание производилось при уменьшающемся давлении газа.

Источник

Печатать книгу

Сайт:	Профильное обучение
Курс:	Физика. 10 класс
Книга:	§ 6. Изотермический, изобарный и изохорный процессы
Напечатано::	Гость
Дата:	Понедельник, 29 Май 2023, 07:30

Свойство газов существенно изменять предоставленный им объём широко используют в тепловых двигателях. Анализируя процессы, происходящие с газом в этих устройствах, важно знать, каким законам подчиняются газы и каковы условия применимости этих законов.

Процессы в газах часто происходят так, что изменяются только два параметра из пяти (p, V, T, m, M). Если при постоянных массе и молярной массе ещё один из макропараметров (p, V, T), входящих в уравнение состояния идеального газа, не изменяется, то такие процессы называют изопроцессами.

Изотермический процесс. Процесс изменения состояния физической системы при постоянной температуре (T = const) называют изотермическим.

Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то из уравнения Клапейрона–Менделеева следует:

Давление данной массы газа при постоянных молярной массе и температуре обратно пропорционально его объёму.

Это утверждение называют законом Бойля–Мариотта.

Справедливость закона Бойля–Мариотта можно продемонстрировать экспериментально, используя установку, представленную на рисунке 18 в § 5.

Если медленно изменять объём газа, находящегося в сосуде, то вследствие теплообмена с окружающей средой можно поддерживать температуру газа в сосуде практически постоянной. При этом уменьшение объёма газа при вращении винта 3 повлечёт за собой увеличение его давления и некоторое незначительное увеличение температуры. И наоборот, увеличение объёма приведёт к уменьшению давления и некоторому незначительному уменьшению температуры газа^*.

От теории к практике

1. Почему пузырьки воздуха, находящиеся в жидкости, поднимаясь вверх, увеличиваются в объёме?

2. Если, не отрываясь, выпить из пластиковой бутылки газированную воду, то можно обнаружить, что бутылка деформируется. Почему?

Рис. 22

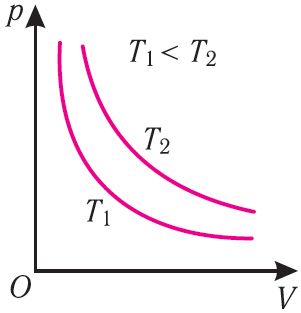
График изотермического процесса, совершаемого идеальным газом, в координатах (p, V) представляет собой гиперболу (рис. 22). В физике такую кривую называют изотермой. Разным значениям температуры газа соответствуют разные изотермы. Согласно соотношениям (6.1) для одинаковых объёмов газов с одинаковыми количествами вещества и разными температурами чем больше давление, тем выше температура (рис. 22).

Многочисленные опыты показали, что исследованные газы подчиняются закону Бойля–Мариотта тем точнее, чем меньше их плотность. При значительном увеличении давления газа этот закон перестаёт выполняться.

От теории к практике

Изобразите графики изотермического процесса в координатах (p, T) и (V, T).

Интересно знать

Лёгкие расположены в грудной клетке, объём которой при дыхании периодически изменяется благодаря работе межрёберных мышц и диафрагмы. К огда грудная клетка расширяется, давление воздуха в лёгких становится меньше атмосферного, и воздух через воздухоносные пути устремляется в лёгкие — происходит вдох. При выдохе объём грудной клетки уменьшается, что вызывает уменьшение объёма лёгких. Давление воздуха в них становится выше атмосферного, и воздух из лёгких устремляется в окружающую среду.

* Незначительное изменение температуры газа принципиально необходимо для теплообмена с термостатом — передача тепла возможна только при разных температурах тел. ↑

Изобарный процесс. Процесс изменения состояния газа при постоянном давлении (p = const) называют изобарным.

В 1802 г. французский учёный Жозеф Гей-Люссак (1778–1850) рассмотрел этот процесс для воздуха, водорода, кислорода и азота.

Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются, то объём газа, как следует из уравнения Клапейрона–Менделеева:

Объём данной массы газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре.

Это утверждение называют законом Гей-Люссака.

Рис. 23

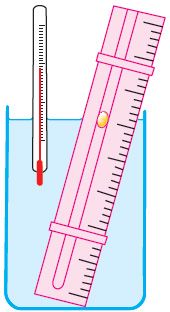
Справедливость закона Гей-Люссака можно продемонстрировать экспериментально, используя установку, представленную на рисунке 23. Жидкость в сосуде находится в тепловом равновесии с тонкой трубкой, заполненной воздухом, запертым капелькой масла. При увеличении температуры жидкости объём воздуха, находящегося в трубке под капелькой масла, возрастает и капелька движется вверх. При уменьшении температуры объём воздуха уменьшается — и капелька движется вниз.

От теории к практике

Можно ли считать расширение газа при медленном нагревании его в цилиндре с подвижным поршнем изобарным процессом?

Рис. 24

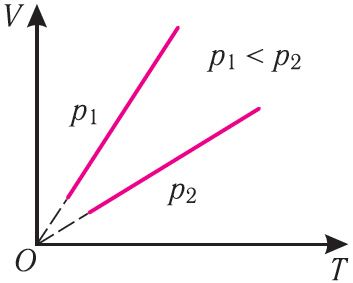
Поскольку V ~ T, то в координатах (V, T) график изобарного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 24). Эту линию называют изобарой.

Изобара реальных газов не может быть продлена до нулевого значения температуры (на графике пунктирная линия), потому что при низких температурах все газы существенно отличаются от модели «идеальный газ» и при дальнейшем уменьшении температуры превращаются в жидкости.

В одних и тех же координатах (V, T) можно построить несколько изобар, которые соответствуют разным давлениям данной массы идеального газа при неизменной молярной массе. Анализ соотношений (6.2) позволяет сделать вывод, что большему давлению соответствует меньший наклон изобары к оси температур (см. рис. 24).

От теории к практике

Изобразите графики изобарного процесса в координатах (p, V) и (p, T).

Изохорный процесс. Процесс изменения состояния газа при постоянном объёме (V = const) называют изохорным.

Впервые этот процесс рассмотрел в 1787 г. французский учёный Жак Шарль (1746–1823)^*.

Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то давление газа, как следует из уравнения Клапейрона–Менделеева:

Давление данной массы газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре.

Это утверждение называют законом Шарля.

Рис. 25

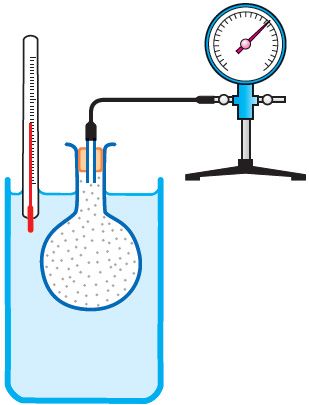
Справедливость закона Шарля можно продемонстрировать экспериментально, используя установку, представленную на рисунке 25. Колба, наполненная воздухом и соединённая с манометром, находится в тепловом равновесии с жидкостью в сосуде. При увеличении температуры жидкости давление воздуха в колбе возрастает, а при уменьшении температуры — давление воздуха уменьшается.

От теории к практике

Идеальный газ определённой массы изохорно охлаждают так, что его температура уменьшается от t₁ = 327 °С до t₂ = 7 °С. Во сколько раз уменьшается давление газа?

Рис. 26

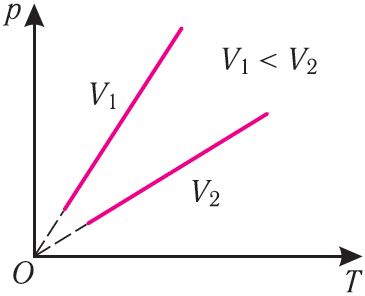
В координатах (p, T) график изохорного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 26). Эту линию называют изохорой.

Как и в случае изобарного процесса, изохора реальных газов не может быть продлена до нулевого значения температуры.

В одних и тех же координатах (p, T) можно построить несколько изохор, соответствующих разным объёмам данной массы газа при неизменной молярной массе. Анализ соотношений (6.3) показывает, что большему объёму соответствует меньший наклон изохоры к оси температур (см. рис. 26).

От теории к практике

Изобразите графики изохорного процесса в координатах (p, V) и (V, T).

1. Как связаны давление и объём идеального газа при изотермическом процессе?

2. Как связаны объём и абсолютная температура идеального газа при изобарном процессе?

3. Как связаны давление и абсолютная температура идеального газа при изохорном процессе?

4. При выполнении каких условий справедлив каждый из законов изопроцессов в реальном газе?

5. Объём идеального газа определённой массы и неизменного химического состава изобарно увеличили в b = 1,5 раза, а затем давление газа изохорно уменьшили в c = 3 раза.

а) Как изменилась абсолютная температура газа в результате первого процесса?

б) Как изменилась абсолютная температура газа в результате второго процесса?

в) Во сколько раз начальная абсолютная температура газа отличается от его конечной температуры?

Рис. 27

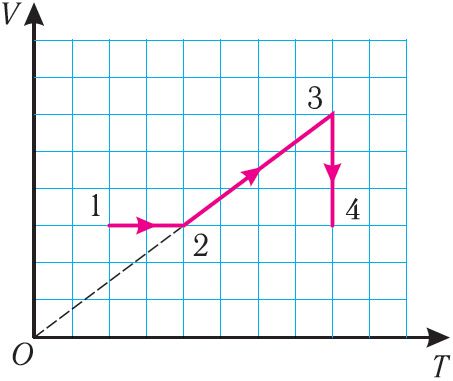
6. На рисунке 27 представлен график трёх процессов изменения состояния идеального газа определённой массы и неизменного химического состава.

а) Какому процессу соответствует участок 1 2 графика? Во сколько раз увеличилось давление газа в этом процессе?

б) Какому процессу соответствует участок 2 3 графика? Во сколько раз увеличились объём и абсолютная температура газа в этом процессе?

в) Какому процессу соответствует участок 3 4 графика? Как и во сколько раз изменились объём и давление газа в этом процессе?

г) Во сколько раз следует уменьшить температуру газа, чтобы изохорно перевести газ из состояния 4 в состояние 2?

* Несмотря на то что Шарль не опубликовал результаты своих исследований, история физики отдаёт приоритет открытия ему. ↑

Примеры решения задач

Решение. На участке 1 2 объём газа прямо пропорционален абсолютной температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика следует, что в состоянии 2 температура и объём газа больше в 4 раза, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом:

переход , , , ,
происходит изобарное нагревание газа.

В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается в 4 раза. Из соотношения (6.3) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его абсолютной температуре. Поэтому можно записать:

переход , , ,
происходит изохорное охлаждение газа.

Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается в 4 раза, что влечёт за собой, согласно закону Бойля–Мариотта, увеличение давления газа в 4 раза:

переход , ,
происходит изотермическое сжатие газа.

Опираясь на сделанные выводы, представим все три процесса в координатах (p, V) и (p, T) (рис. 29, а, б).

Рис.

Рис. 29

Пример 2. При изотермическом расширении идеального газа определённой массы его объём увеличился от V₁ = 2,0 л до V₂ = 5,0 л, а давление уменьшилось на Δp = –15 кПа. Определите первоначальное давление газа.

Дано:
V₁ = 2,0 л = 2,0 · 10^–3 м³
V₂ = 5,0 л = 5,0 · 10^–3 м³
Δp = –15 кПа = –1,5 · 10⁴ Па

р₁ — ?

Решение: Так как температура и масса газа не изменяются, то его начальное и конечное состояния связаны законом Бойля–Мариотта, т. е. . С учётом того, что , получим:

Откуда $fraction numerator increment p V subscript 2 over denominator V subscript 1 minus V subscript 2 end fraction$ .

$p subscript 1 space equals space fraction numerator negative 1 comma 5 times 10 to the power of 4 space Па times 5 comma 0 times 10 to the power of negative 3 end exponent space straight м cubed over denominator 2 comma 0 times 10 to the power of negative 3 end exponent space straight м cubed minus 5 comma 0 times 10 to the power of negative 3 end exponent space straight м cubed end fraction space equals space 2 comma 5 times 10 to the power of 4 space Па space equals space 25 space кПа$ .

Ответ: .

Пример 3. В двух сосудах вместимостью V₁ = 20 л и V₂ = 30 л находятся химически не реагирующие идеальные газы, давления которых p₁ = 1,0 МПа и p₂ = 0,40 МПа соответственно. Определите давление газов в сосудах после того, как их соединили тонкой короткой трубкой. Температура газов до и после соединения сосудов одинаковая.

Дано:
V₁ = 20 л = 2,0 · 10^-2 м³
V₂ = 30 л = 3,0 · 10^-2 м³
p₁ = 1,0 МПа = 1,0 · 10⁶ Па
p₂ = 0,40 МПа = 4,0 · 10⁵ Па
T = const

р — ?

Решение: Давление смеси газов равно сумме парциальных давлений (закон Дальтона): . Найдём парциальное давление каждого газа после соединения сосудов. Так как температура и массы газов не изменяются, то начальное и конечное состояния каждого газа связаны законом Бойля–Мариотта, т. е.

, .

Следовательно, парциальные давления газов после соединения сосудов: $p subscript 1 superscript apostrophe equals fraction numerator p subscript 1 V subscript 1 over denominator V subscript 1 plus V subscript 2 end fraction$ , $p subscript 2 superscript apostrophe equals fraction numerator p subscript 2 V subscript 2 over denominator V subscript 1 plus V subscript 2 end fraction$ . Тогда $p equals fraction numerator p subscript 1 V subscript 1 plus p subscript 2 V subscript 2 over denominator V subscript 1 plus V subscript 2 end fraction$ .

$p equals fraction numerator 1 comma 0 times 10 to the power of 6 space Па times 2 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed plus 4 comma 0 times 10 to the power of 5 space Па times 3 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed over denominator 2 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed plus 3 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed end fraction equals 6 comma 4 times 10 to the power of 5 space Па equals 0 comma 64 space МПа.$

Ответ: p = 0,64 МПа.

Упражнение 5

1. При изобарном увеличении температуры идеального газа, находящегося в герметично закрытом цилиндре, на ΔT = 60,0 К его объём увеличился в β = 1,21 раза. Определите начальную абсолютную температуру газа.

2. Изобразите графически процесс изобарного охлаждения определённой массы идеального газа в координатах (p, T); (V, T); (V, p).

3. Идеальный газ определённой массы сначала изобарно расширили, а затем изотермически сжали до первоначального объёма. Изобразите графически эти процессы в координатах (V, T); (p, V).

Рис. 30

4. На рисунке 30 представлен график изменения состояния определённой массы идеального газа. (Переход 3 1 осуществляется при неизменной температуре.) Изобразите графически этот процесс в координатах (T, V) и (p, T).

5. При температуре t₁ = –3,0 °С манометр на баллоне со сжатым кислородом показывал давление p₁ = 1,8 · 10⁶ Па, а при температуре t₂ = 27 °С — давление p₂ = 2,0 · 10⁶ Па. Определите, была ли утечка газа из баллона.

6. В герметичном сосуде, заполненном воздухом (), лежит полый металлический шарик, диаметр которого d = 4,0 см, а масса m = 0,64 г. Определите минимальное значение давления воздуха, накачиваемого в сосуд, при котором бы шарик поднялся вверх, если температура t = 17 °С остаётся постоянной.

7. Идеальный газ, давление которого p₁ = 4 · 10⁵ Па, занимал объём V₁ = 2 л. Сначала газ изотермически расширили до объёма V₂ = 8 л, а затем изохорно нагрели, в результате чего его абсолютная температура увеличилась в α = 3 раза. Определите давление р₃ газа в конце процесса, если при переходе из начального состояния в конечное масса газа оставалась неизменной.

Источник

Закон Бойля-Мариотта — один из фундаментальных законов физики и химии, который связывает изменения давления и объема газообразных веществ. При помощи нашего калькулятора легко решить простые задачи по физике или химии.

Закон Бойля-Мариотта

Изотермический газовый закон был открыт ирландским ученым Робертом Бойлем, который проводил опыты над газами под давлением. При помощи U-образной трубки и обычной ртути Бойль установил простую закономерность, что в каждый момент времени произведение давления на объем газа неизменно. Если говорить сухим математическим языком, то закон Бойля-Мариотта гласит, что при неизменной температуре произведение давления и объема постоянно:

P×V = const.

Для сохранения постоянного соотношения величины должны изменяться в разные стороны: во сколько раз уменьшится одна величина, во столько же раз увеличится другая. Следовательно, давление и объем газа обратно пропорциональны и закон можно переписать в следующем виде:

P1×V1 = P2×V2,

где P1 и V1 — начальные значения давления и объема соответственно, а P2 и V2 — конечные значения.

Применение закона Бойля-Мариотта

Наилучшей иллюстрацией проявления открытого Бойлем закона является погружение пластиковой бутылки под воду. Известно, что если газ помещен в баллон, то давление на вещество будет определяться только стенками баллона. Другое дело, когда это пластичная бутылка, которая легко изменяет свою форму. На поверхности воды (давление 1 атмосфера) закрытая бутылка будет сохранять свою форму, однако при погружении на глубину 10 м на стенки сосуда будет действовать давление в 2 атмосферы, бутылка начнет сжиматься, а объем воздуха уменьшится в 2 раза. Чем глубже будет погружаться пластиковая тара, тем меньший объем будет занимать воздух внутри нее.

Это простая демонстрация действия газового закона иллюстрирует важный вывод для многих дайверов. Если на поверхности воды баллон с воздухом имеет емкость 20 л, то при погружении на глубину 30 м, воздух внутри сожмется в три раза, следовательно, воздуха для дыхания на такой глубине будет в три раза меньше, чем на поверхности.

Помимо дайверской темы, закон Бойля-Мариотта в действии можно наблюдать в процессе сжатия воздуха в компрессоре или в расширении газов при использовании насоса.

Наша программа представляет собой онлайн-инструмент, при помощи которого легко рассчитать пропорцию для любого газового изотермического процесса. Для использования инструмента вам требуется знать три любые величины, а калькулятор автоматически рассчитает искомую.

Примеры работы калькулятора

Школьная задача

Рассмотрим простую школьную задачку, в которой требуется найти первоначальный объем газа, если давление изменилось с 1 до 3 атмосфер, а объем уменьшился до 10 л. Итак, у нас есть все данные для расчета, которые требуется ввести в соответствующие ячейки калькулятора. В итоге получаем, что первоначальный объем газа составлял 30 литров.

Еще о дайвинге

Вспомним пластиковую бутыль. Представим, что мы погрузили бутыль, наполненную 19 л воздуха на глубину 40 м. Как изменится объем воздуха на поверхности? Это более сложная задачка, но только потому, что нам требуется перевести глубину в давление. Мы знаем, что на поверхности воды атмосферное давление составляет 1 бар, а при погружении в воду давление увеличивается на 1 бар каждые 10 м. Это означает, что на глубине 40 м бутыль будет под давлением приблизительно 5 атмосфер. У нас есть все данные для расчета, и в результате мы увидим, что объем воздуха на поверхности увеличится до 95 литров.

Заключение

Закон Бойля-Мариотта встречается в нашей жизни довольно часто, поэтому вам несомненно пригодится калькулятор, который автоматизирует расчеты по этой простой пропорции.

Источник

Закон Бойля – Мариотта – один из основных газовых законов, открытый в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году. Закон является частным случаем уравнения состояния идеального газа.

Закон Бойля – Мариотта гласит: при постоянной температуре и массе идеального газа произведение его давления и объема постоянно. В математической форме это утверждение записывается следующим образом:

(pV = const),

где (p) – давление газа; (V) – объем газа.

Важно уточнить, что в данном законе газ рассматривается, как идеальный. На самом деле, все газы в той или иной мере отличаются от идеального. Чем выше молекулярная масса газа, тем больше это отличие.

Закон Бойля – Мариотта, закон Шарля и закон Гей-Люссака, дополненные законом Авогадро, образуют уравнение состояния идеального газа.

Закон Шарля – объем газа при постоянном давлении прямо пропорционален его абсолютной температуре. Эта зависимость была впервые выведена Жаком Шарлем в 1787 г. Его иногда называют законом Гей-Люссака, поскольку Жозеф Гей-Люссак заново вывел его и уточнил в 1802 г.

Закон Гей-Люссака – закон пропорциональной зависимости объема газа от абсолютной температуры при постоянном давлении, названный в честь французского физика и химика Жозефа Луи Гей-Люссака, впервые опубликовавшего его в 1802 году (в англоязычной литературе закон Гей-Люссака обычно называют законом Шарля и наоборот). Кроме того, законом Гей-Люссака называют также химический закон объемных отношений.

Процесс, протекающий при постоянном давлении, называется изобарным. На диаграмме в координатах t этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах р, t он изображается прямой, называемой изохорой. Процесс, протекающий при постоянной температуре, называется изотермическим. На диаграмме р, V этот процесс изображается прямой, называемой изотермой.

Работа – это один из способов изменения внутренней энергии, легко рассчитать работу газа в изобарном процессе. На данном этапе необходимо подчеркнуть, что сила давления газа на всем пути не меняется и, по третьему закону Ньютона, (|F_2| = |F_1|), знак работы находим из формулы (A = Fs cosα.) Если (α = 0^{circ}), то (A > 0), если (α = 180^{circ}), то (A < 0). На графике зависимости (р(V)) работа численно равна площади под графиком.

Пусть газ расширяется или сжимается изотермически. Например, газ сжимается под поршнем, давление изменяется, и в любой момент времени (p=frac vVRT.)

При бесконечно малом перемещении поршня на (dl) мы получим бесконечно малое изменение объема (dV), а давление р можно считать постоянным. По аналогии с нахождением механической работы переменной силы, составим простейшее дифференциальное соотношение (dA = pdV), тогда (A=intlimits_{V_1}^{V_2}pdV,) и, зная зависимость (p (V)), запишем (A=intlimits_{V_1}^{V_2}vRTfrac {dV}V.) Это табличный интеграл типа (intlimits_{x_1}^{x_2}frac{dx}x). Работа газа в этом случае отрицательна, т. к. (alpha = 180^circ):

(A=vRTlnfrac{V_2}{V_1}<0,)

т. к. (V_2 < V_1). Полученную формулу можно переписать, используя соотношение

(frac {V_2}{V_1}=frac{p_1}{p_2}.)

Чем можно пренебречь в случае идеального газа?
В цилиндре под поршнем изобарически охлаждают (10) л газа от (127^{circ}C) до (7^{circ}C). Объем охлажденного газа равен
Изобарно увеличили температуру (2) молей идеального газа с (20) до (120^{circ}C). Количество теплоты, которое было при этом сообщено, равно ((R = 8,31) Дж/(моль · К)
Чтобы изобарно увеличить объем двух молей идеального одноатомного газа в (5) раз, ему необходимо передать количество теплоты, равное
При постоянном давлении (10^5) Па объем воздуха, находящегося в помещении, увеличился на (200) дм(^3). При этом газ совершил работу, равную
В закрытом сосуде при температуре (150) К находится (6) моль одноатомного идеального газа. Если средняя квадратичная скорость его молекул возросла в (1,5) раза, то газу передано количество теплоты, равное ((R=8,31)Дж/(моль · К))
Работа идеального газа равна нулю в процессе
Изобарному процессу соответствуют участки
На графиках представлены процессы
Если в теплоизолированном сосуде газ сжимается, то температура газа
Чтобы при постоянном давлении объем газа увеличился в (2) раза, его температуру нужно
В закрытом сосуде при температуре (27^{circ}C) находится (3) моль одноатомного идеального газа. Если средняя квадратичная скорость его молекул возросла в (1,5) раза, то газу передано количество теплоты, равное
Газ в количестве 1 кмоль при давлении 1 МПа и температуре 127°C занимает объем ( R = 8,31 Дж/(моль · К)
Газ совершает работу при переходе из состояния (1) в состояние (3). Если (p_1=0,1) МПа, (V_1=1) л, (T_2 =2T_1), (T_3 =2T_2), то работа газа равна
При постоянном давлении (2cdot10^5) Па объем воздуха, находящегося в помещении, увеличился на (2) м(^3). При этом газ совершил работу, равную
Если концентрация газа увеличится в (3) раза, а скорость уменьшится в (3) раза, то его давление
Идеальный газ сначала нагревался при постоянном объеме, потом его объем увеличивался при постоянном давлении, затем при постоянной температуре давление газа уменьшалось до первоначального. Эти изменения представлены
На увеличение внутренней энергии газа пошло (10%) подведенного к нему тепла. Если его внутренняя энергия возросла на (4) кДж, то газ совершил работу, равную
Газ при температуре (273^{circ}C) занимает объем в (4) м(^3). Какой объем занимает этот газ при температуре (546^{circ}C) и при прежнем давлении?
Что приводит к изменению внутренней энергии идеального газа при данной массе?
На каком из ниже представленных рисунков изображена изобара идеального газа?
Определите работу по ниже представленному рисунку, если газ перешел из состояния (1) в состояние (3) в процессе (1-2-3.)
На увеличение внутренней энергии газа пошло (30%) подведенного к нему тепла. Какую работу совершил газ, если его внутренняя энергия возросла на (3) кДж?
За счет какого процесса совершается работа при адиабатном расширении идеального газа?
Определите количество теплоты, необходимое для изобарного увеличения объема пяти молей идеального одноатомного газа в (4) раза.
Если при температуре (27^{circ}C) давление газа в закрытом сосуде равнялось (90) кПа, то какое давление будет у газа при температуре (t=-23^{circ}C)?
Идеальный газ имеет температуру (T_0 = 150) К и давление (P_0= 0,!8) кПа. Не меняя массу и объем газа, температуру уменьшили на (25%). Как при этом изменилось давление газа?
Физическую величину, определяемую выражением (frac{mRT}{MV}), можно измерить в таких единицах измерения, как
Во сколько раз увеличится давление газа в баллоне, если его нагреть от (-330^{circ}C) до (+330^{circ}C)?
Когда объем газа уменьшили на (50) мл, его давление возросло в (3) раза. Каков был его первоначальный объем?
Газ занимает объем в (2) м(^3) при нормальных условиях. Его изотермически сжали до давления в (9,8) МПа. Какой объем теперь занимает газ?
На графике представлена зависимость давления от температуры идеального одноатомного газа. Выберите правильные утверждения.
(5) молей идеального одноатомного газа, который находился при температуре (+27^{circ}C), не меняя давление, нагрели. Абсолютная температура газа при этом увеличилась в (4) раза. Какое количество теплоты было сообщено этому газу? (Универсальная газовая постоянная – (8,!31 frac{Дж}{мольcdot К})).
Не меняя температуры, объем газа уменьшили в (6) раз. Давление газа (P_2) при этом по отношению к первоначальному давлению (P_1)
Уравнение Менделеева – Клапейрона может быть записано в виде
Найдите начальную температуру газа, если при уменьшении его объема на (20%) его давление возросло на (40%), а температура увеличилась на (36) К.
В закрытом баллоне находится газ под давлением (10) кПа. Если температура газа повысится в (2) раза, чему станет равным давление газа?
Как изменится температура газа, если, не меняя давления, его объем увеличить в полтора раза?