- Главная
- Справочники
- Справочник по математике для начальной школы
- Вычитание
Познакомимся с вычитанием.
Рассмотрим числовой ряд и вспомним, в каком порядке идут числа.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
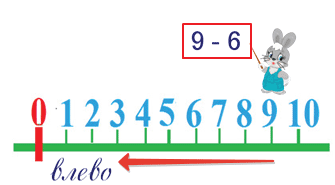
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Вычитает число 6.
Из какого числа он вычитает число 6?
Из числа 9. Мы поставили зайчика на число 9.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 6.
На каком делении он остановится? На числе 3.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
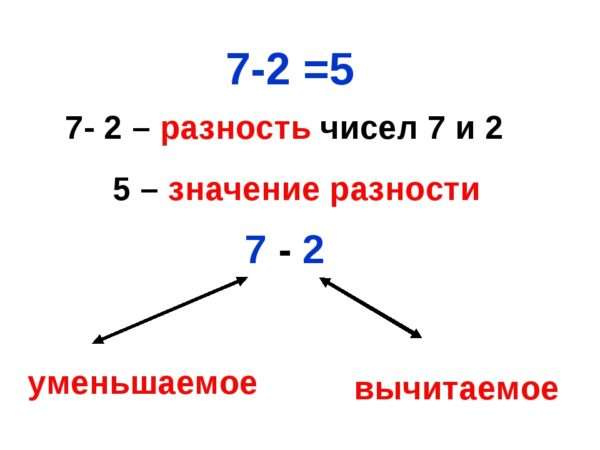
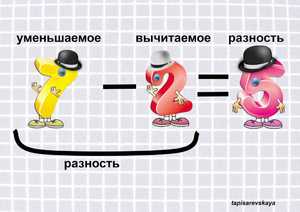
9 — 6 = 3
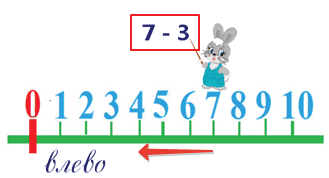
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Вычитает число 3.
Из какого числа он вычитает число 3?
Из числа 7. Мы поставили зайчика на число 7.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 3.
На каком делении он остановится? На числе 4.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
7 — 3 = 4
Как называются числа при вычитании?
Число, из которого вычитают, становится МЕНЬШЕ, уменьшается, поэтому его называют «уменьшаемое».
Число, которое вычитают, называют «вычитаемое».
Число, которое получается в результате вычитания, называют «разность».
Рассмотри рисунок.
У жонглёра было 9 шариков.
Когда несколько шариков упало, осталось ещё 5 шариков.
Сколько шариков упало?
Каким действием будем находить? Вычитанием.
9 — 4 = 5
Как называются числа при вычитании?
9 — уменьшаемое
4 — вычитаемое
5 — разность
Как найти неизвестное вычитаемое
Рассмотри рисунок.
У жонглера было 9 шариков. Когда несколько шариков упало, осталось 5. Упали, значит, убрали.
Решаем вычитанием. Что нужно найти?
Нужно найти вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
9 — 5 = 4
Вычитаемое равно 4.
Упало 4 шарика.
Как найти неизвестное уменьшаемое
Что известно?
Вычитаемое — 4.
Разность — 5.
Нужно найти уменьшаемое.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
5 + 4 = 9
Проверка вычитания
Если к разности прибавить вычитаемое, получится уменьшаемое.
Именно эта связь между разностью, уменьшаемым и вычитаемым используют для проверки вычитания.
Например, 35 — 15 = 20.
Правильно ли произведено вычисление? Можно проверить так:
20 + 15 = 35, мы к разности прибавили вычитаемое и получили уменьшаемое. Значит, вычисление произведено верно и пример решен правильно.
Советуем посмотреть:
Табличное вычитание
Письменное вычитание в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 38,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 47,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 53,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 68,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 83,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32. Урок 21,
Петерсон, Учебник, часть 1
Страница 13. Урок 7,
Петерсон, Учебник, часть 2
Страница 47. Урок 24,
Петерсон, Учебник, часть 2
Страница 72. Урок 37,
Петерсон, Учебник, часть 3
Страница 91. Повторение,
Петерсон, Учебник, часть 3
2 класс
Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 68,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 110,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 9,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 19. Урок 9,
Петерсон, Учебник, часть 1
3 класс
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 11,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 18,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 8. Урок 2,
Петерсон, Учебник, часть 1
Страница 42. Урок 16,
Петерсон, Учебник, часть 2
Страница 32. Урок 15,
Петерсон, Учебник, часть 3
Страница 37. Урок 17,
Петерсон, Учебник, часть 3
4 класс
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 68,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 9. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 41. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 83. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 85. Тест 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
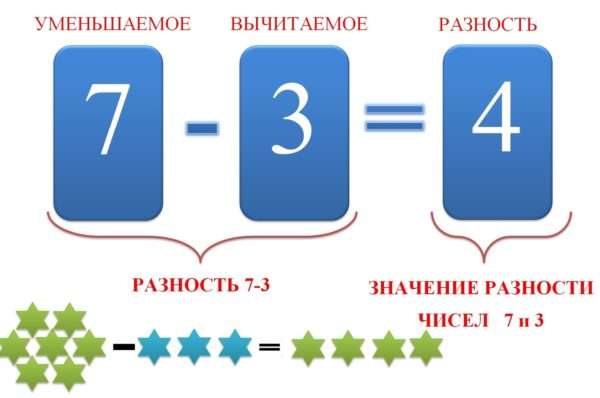
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | 11 | = | 7 | |
| 14 | 5 | = | 9 | |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Найти неизвестное вычитаемое можно двумя способами. Лучше всего, конечно, знать правило:
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Как быть, если правило забылось? Поможет такой способ: нужно придумать легкий пример на вычитание, понять, что нужно сделать, чтобы в нем найти вычитаемое, и точно так же поступить для нахождения вычитаемого в своем примере.
Например: 7-3=4. Здесь вычитаемое — 3. Чтобы найти 3, нужно из 7 вычесть 4.
Рассмотрим, как найти вычитаемое, на примерах:
1)
| 75 | — | x | = | 28 |
| ум. | в. | р. |
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого отнять разность:
x=75-28
x=47
Ответ:47.
2)
| 432 | — | t | = | 300 |
| ум. | в. | р. |
Чтобы найти вычитаемое, из уменьшаемого вычитаем разность:
t=432-300
t=132
Ответ: 132.
Позже мы рассмотрим более сложные примеры, в которых, помимо вычитания, будут и другие действия.
Вычитание чисел
Что такое вычитание?
Вычитание – это арифметическое действие обратное сложению, посредством которого из одного числа вычитают (отнимают) столько единиц, сколько их содержится в другом числе.
Число, из которого вычитают, называется уменьшаемым, число, которое указывает сколько единиц будет вычтено из первого числа, называется вычитаемым. Число, получаемое в результате вычитания, называется разностью (или остатком).
Рассмотрим вычитание на примере. На столе лежит 9 конфет, если съесть 5 конфет, то их останется 4. Число 9 является уменьшаемым, 5 – вычитаемым, а 4 – остатком (разностью):
Для записи вычитания используется знак — (минус). Он ставится между уменьшаемым и вычитаемым, при этом уменьшаемое записывается слева от знака минус, а вычитаемое – справа. Например, запись 9 — 5 означает, что из числа 9 вычитается число 5. Справа от записи вычитания ставят знак = (равно), после которого записывают результат вычитания. Таким образом, полная запись вычитания выглядит так:
Эта запись читается так: разность девяти и пяти равняется четырём или девять минус пять равно четыре .
Чтобы в результате вычитания получить натуральное число или 0, уменьшаемое должно быть больше вычитаемого или равно ему.
Рассмотрим, как, используя натуральный ряд, можно выполнить вычитание и найти разность двух натуральных чисел. Например, нам необходимо вычислить разность чисел 9 и 6, отметим в натуральном ряду число 9 и отсчитаем от него влево 6 чисел. Получим число 3:
Вычитание также можно использовать для сравнения двух чисел. Желая сравнить между собой два числа, мы задаёмся вопросом, на сколько единиц одно число больше или меньше другого. Чтобы узнать это, надо из большего числа вычесть меньшее. Например, чтобы узнать, на сколько 10 меньше 25 (или на сколько 25 больше 10), надо из 25 вычесть 10. Тогда найдём, что 10 меньше 25 (или 25 больше 10) на 15 единиц.
Проверка вычитания
где 15 – это уменьшаемое, 7 – это вычитаемое, а 8 – разность. Чтобы узнать правильно ли было выполнено вычитание, можно:
-
вычитаемое сложить с разностью, если получится уменьшаемое, то вычитание было выполнено верно:
от уменьшаемого отнять разность, если получится вычитаемое, то вычитание было выполнено верно:
Как найти разность чисел в математике

Арифметические действия с числами
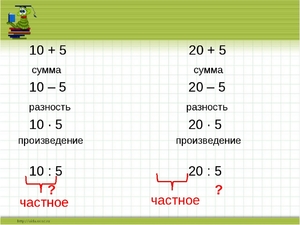
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
- сумма — результат, получившийся при сложении чисел;
- разность — результат, получившийся при вычитании чисел;
- произведение — результат умножения чисел;
- частное — результат деления.
Это интересно: что такое модуль числа?
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
- сумма — прибавить;
- разность — отнять;
- произведение — умножить;
- частное — разделить.
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
Разность чисел означает, насколько одно из них больше другого.
- Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
- Это вычитание одного числа из другого.
- Это цифра, составляющая остаток при минусовании двух величин.
- Это величина, являющаяся результатом вычитания двух значений.
- Разность показывает количественное различие между двумя цифрами.
- Это результат одного из четырёх арифметических действий, которым является вычитание.
- Это то, что получится, если из уменьшаемого отнять вычитаемое.
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
- Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
- Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
- Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
- Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
- Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
- Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Простые примеры
- Пример 1. Найти разницу двух величин.
20 — уменьшаемое значение,
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.
- Пример 2. Найти уменьшаемое.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
- Пример 3. Найти вычитаемое значение.
17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
- Пример 4. Найти разницу трёх значений.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
Ответ: 40 — разница трёх значений.
- Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
- Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
- Удвоенное число — это величина, умноженная на два.
- Утроенное число — это величина, умноженная на три.
- Удвоенная разность — это разница величин, умноженная на два.
- Утроенная разность — это разница величин, умноженная на три.
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
- Пример 7. Найти разницу величин 7 и 18.
7 — уменьшаемая величина;
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
- Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых;
- произведение — умножением множителей;
- частное — делением делимого на делитель.
Вот такая интересная арифметика.
Слагаемое, сумма; уменьшаемое, вычитаемое, разность.
Вы здесь: Главная 



Автор: Юргель Ольга Александровна
1 класс (1-4)
- закрепить знание названий компонентов сложения и вычитания; продолжить работу по формированию прочных, осознанных, доведенных до автоматизма навыков вычислений в пределах 20;
- развивать математическую речь учащихся;
- воспитывать аккуратность при работе в тетради.
Оборудование: изображение инопланетян, буквы с примерами, линейка с рисунками и примеры к ней.
Сегодня к нам на урок прилетели гости. Это необычные гости. Хотите отгадать, кто это? Для этого нужно решить примеры на карточках с буквами и поставить их по порядку под соответствующими числами:
Дети решают примеры на карточках (сложение и вычитание в пределах 20 с ответами от 1 до 12, в соответствии с таблицей). Читают появившееся слово: инопланетяне.
— Правильно! Это инопланетяне. А вот и они. (На доску прикрепляется изображение инопланетян.)
Приземление состоялось. Они пока еще не знают нашего языка и говорят со мной мысленно. Это называется телепатией. Они говорят мне, что хотят изучить Землю и людей. И они хотят познакомиться с вами.
Первое, что они хотят исследовать, это ваша сообразительность. Для этого они просят представить в виде десятков и единиц числа. А какие это числа, попробуем мысленно прочитать. Инопланетяне посылают нам сигнал. Ну-ка, кто угадает числа?
Дети называют числа, если число двузначное, значит, верно прочитали мысли. Число представляют в виде суммы разрядных слагаемых.
На планете, где живут наши гости, вместо цифр используются другие значки. Посмотрите, они привезли с собой линейку:
а) Сравните числа: листочек и вишенка; груша и звездочка; морковка и флажок; солнышко и гриб.
Записываются неравенства с использованием данных значков.
б) Решите примеры:
Записывают примеры на доске.
А теперь давайте-ка покажем, как мы умеем решать наши земные примеры:
Дети решают примеры на счетных веерах.
III Работа над темой урока.
— А теперь внимание, инопланетяне мысленно стараются помочь вам получше запомнить компоненты сложения. Как называются числа, которые мы складываем?(Слагаемые.)
Дети повторяют сначала тихо, потом все громче и громче.
— Как называется результат сложения? (Сумма.)
Назовите слагаемые и сумму:
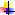

— А теперь решите-ка вот этот пример:
Теперь почувствуйте, как ваша память снова включается. Почувствовали?
19 – это уменьшаемое.
Как вы думаете, почему этот компонент так назвали? (Потому что это число будет меньше, когда вычтем.)
4 – это вычитаемое. (Хором)
Почему так называется? (Мы его вычитаем.)
— А то, что получилось в результате – это разность. (Хором.)
Примеры № 4 (Дети работают в парах.)
Найдите примеры, где в результате должна получиться сумма. Запишите и решите любой. А теперь объясните соседу, где слагаемые, а где сумма.
Найдите примеры, где в ответе получится разность. Запишите и решите любой. Объясните соседу, где уменьшаемое, где вычитание, а где разность.
Решение уравнений. Нахождение неизвестного вычитаемого. 1-й класс
Цель урока: знакомство с правилом нахождения неизвестного вычитаемого.
1) Продолжить формирование умения решать уравнения с неизвестными слагаемыми; учить решать уравнения с неизвестными вычитаемыми. Сравнить данные типы уравнений через взаимосвязь действий сложения и вычитания.
2) Развивать операции мышления (анализ, синтез, сравнение, классификацию), моделирующую деятельность, пространственное мышление.
3) Формировать систему ценностей, направленную на максимальный вклад каждого в коллективную деятельность.
Методы обучения: проблемно-поисковый метод.
Формы познавательной деятельности учащихся: сочетание фронтальной формы работы с групповой и индивидуальной.
Учебник математики 1 класс. Аргинская И.И.
Демонстрационный материал: таблица с латинскими буквами, таблица с понятием уравнения, магнитофон для физкультминутки.
Содержание урока:
1. Организационный момент.
Организация класса, проверка готовности к уроку, задание положительной мотивации.
– Каждый урок – открытие. Сегодня мы будем открывать для себя что-то новое. Это новое связано с понятием “равенство” и “неизвестное число”. Догадались, о чём пойдёт речь на уроке? ( Об уравнениях.) Что такое уравнение? ( Равенство, в котором есть неизвестное число.)
Как всегда на уроке будем повторять то, что нами уже было открыто.
На доске числа: 15, 7 ,8.
Что вы можете о них сказать?
Дети: 7 и 8 – однозначные числа, 15 – двузначное число. С ними можно составить выражения.
– Составьте, пожалуйста, запишите в тетради. Что получилось?
Проверка на доске.
– Что мы сейчас вспомнили?
Дети: Что действия сложения и вычитания взаимосвязаны.
– Измените первое равенство так, чтобы второе слагаемое было неизвестно. Что получилось? (Уравнение.) Решите его.
Проверка на доске.
Как мы находим неизвестное слагаемое?
Дети: Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
– Измените третье равенство так, чтобы вычитаемое было неизвестно.
Что получилось? (Уравнение.)
Проверка на доске.
– Как его решить? Что неизвестно? (Вычитаемое.) Чему в третьем равенстве равно вычитаемое? (7) Как получить 7?
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть значение разности.
Чем похожи уравнения?
Дети: В них одинаковые числа. И решаются они одинаково, действием вычитания.
А теперь правило решения уравнения с неизвестным вычитаемым прочитайте в учебнике на странице 118 № 293
– Сравните пары уравнений. Какая между ними связь?
5. Закрепление. Рефлексия.
Решите в тетради первое и второе уравнения № 293 по вариантам.
Проверка решения на доске.
Дома составите три своих уравнения с неизвестными вычитаемыми и решите их.
Под музыку учитель спокойно и медленно говорит.
“Сядьте поудобнее, расслабьтесь, закройте глаза, руки на колени ладонями вверх, представляйте всё, о чём я буду говорить.
Представьте в себе сердце маленькую звёздочку. Эта звёздочка состоит из двух половинок. Первая половина – то, о чём вы мечтаете и на что надеятесь. Вторая – то, что вы делаете, чтобы добиться успеха. Рисуйте до тех пор, пока не почувствуете, что достигли цели и вам удалось то, к чему вы стремились. Мысленно порадуйтесь: “Я заслужил удачу!” Откройте глаза и скажите уверенно вслух: “Я смогу сделать то, что мне надо сделать!”
1)Выделение “лишнего объекта”
Задание №295 на странице 119.
Назови “лишний” рисунок. Объясни свой ответ.
“Лишний левый рисунок в нижнем ряду, потому что там дети идут в школу, а на остальных – из школы” “А ещё он лишний, потому что на нём дети идут, а на остальных – стоят”.
“Лишний рисунок левый в верхнем ряду, там дом, а на остальных школа”.
“Лишний рисунок правый в нижнем ряду, там зима, на остальных лето”.
“Лишний рисунок правый в верхнем ряду, на нём мальчиков меньше чем девочек, на остальных – поровну”.
“Лишний рисунок средний в верхнем ряду, там все дети разговаривают, на других – один говорит – другие слушают”.
2) Виды многоугольников.
– Как называется фигура? (треугольник)
– Можно назвать по-другому? (многоугольник)
– А ещё? Когда мы ещё не знали многоугольников, как называли такие фигуры? (замкнутые ломаные линии)
Что можно сказать о латинских буквах, которые использованы для обозначения фигур? ( Они пишутся так, же как и русские) Назовите буквы, которые и читаются как русские. (М,А,О,К)
МАН, МНВ, МАВ, МОС, МСК, МОК.(6)
Сколько других многоугольников?
НАОС, ВНСК, ВАОК.(3)
Сколько всего? Запишем выражение.
3) Двузначные числа. Разряд десятков.
20 21 22 23 24 25 26 27 28 29
10 11 12 13 14 15 16 17 18 19
– Чем похожи, чем различаются числа первой и второй строки? ( У них разные цифры в разряде единиц, и разные – в разряде десятков)
– На сколько, каждое число второй строки, меньше числа стоящего над ним?
– Какое общее название подходит всем числам? (двузначные)
– Дальше задание будете выполнять двумя группами.
Работать будем с числами второй строки. Первая группа выпишет числовой ряд, в котором первое число – наименьшее двузначное число, всего в ряду – 5 чисел. Вторая группа запишет числовой ряд – первое число которого – сумма чисел 8 и 7, в ряду 5 чисел.
– Уменьши на 10 каждое число числового ряда. Запиши результат
7. Вычитание натуральных чисел и его свойства. Правила
В вазе лежало 15 мандаринов. Мы с друзьями съели 7 штук.
Сколько мандаринов осталось в вазе?
Понятно, что если к оставшемуся количеству ( х ) добавить 7 мандаринов,
их снова станет 15 .
Значит нам известно одно слагаемое и сумма ,
а второе слагаемое надо найти.
Для этого в математике есть действие. Оно называется вычитание,
х = 15 – 7 = 8 ; так как 8 + 7 = 15 .
15 — уменьшаемое, 7 — вычитаемое, 8 — разность.
Число, из которого вычитают, называют уменьшаемым,
а число, которое вычитают, вычитаемым.
Результат вычитания называют разностью.
Если мы используем натуральные числа, то уменьшаемое обязательно
должно быть больше вычитаемого.
Разность двух чисел показывает, на сколько уменьшаемое
больше вычитаемого, или,
на сколько вычитаемое меньше уменьшаемого.
9 больше 4 на 5 .
243 – ( 143 + 39 ) = 243 – 182 = 61.
Но гораздо удобнее считать так:
243 – ( 143 + 39 ) = 243 – 143 – 39 = 100 – 39 = 61.
Значит: a – ( b + c ) = a – b – c .
В этом выражении мы вычитаем сумму из числа, можно сделать иначе,
сначала вычесть из уменьшаемого одно слагаемое, а потом
из полученной разности второе слагаемое.
Такое свойство называют свойством вычитания суммы из числа.
Рассмотрим еще пример:
371 – 55 – 45 = 316 – 45 = 271 .
Но удобнее найти сумму вычитаемых и вычесть ее из уменьшаемого:
371 – 55 – 45 = 371 – ( 55 + 45 ) = 371 – 100 = 271 .
Рассмотрим еще три примера с одинаковыми результатами.
( 5 + 4 ) – 3 = 9 – 3 = 6 ;
5 + ( 4 – 3 ) = 5 + 1 = 6 ;
( 5 – 3 ) + 4 = 2 + 4 = 6 .
значит: ( 5 + 4 ) – 3 = 5 + ( 4 – 3 ) = ( 5 – 3 ) + 4 .
или: ( a + b ) – c = a + ( b – c ) , если с
3) 523 – ( 250 + 123 ) =
Решите примеры удобным способом и заполните поля :
1) 242 – 63 – 37 = 242 –
2) 761 – 46 – 314 = 761 –
3) 436 – 209 – 121 = 436 –
Вычислите, выбирая удобный порядок выполнения действий.
1) 87 – 49 – 27 = 60 –
2) 120 – 64 – 36 = 120 –
3) 88 – 53 – 18 = 70 –
4) 43 – 15 – 25 = 43 –
Найдите значение выражения, применяя для упрощения вычислений свойства вычитания.
1) 339 – ( 150 + 139 ) = 200 –
2) 851 – 467 – 233 = 851 –
3) 423 – 145 – 255 = 423 –
4) 572 – ( 90 + 372 ) = 200 –
Выберите верное числовое выражение.
1) 173 – 84 2) 70 + 29 3) 184 – 84 Неверно. Не кликай на пустое поле. Неверно. 356 + 67 – 156 =
1) 200 + 67 2) 433 – 156 3) 424 – 156 Неверно. Неверно. Не кликай на пустое поле. 248 – ( 148 + 17 ) =
1) 248 – 175 2) 248 – 164 3) 100 – 17 Неверно. Неверно. Неверно. Не кликай на пустое поле. Неверно. Неверно. 185 – 57 – 23 =
1) 185 – 80 2) 127 – 23 3) 138 – 23 Неверно. Не кликай на пустое поле. 329 – ( 129 + 50 ) =
1) 329 – 179 2) 200 + 50 3) 200 – 50 Неверно. Неверно. Неверно. Не кликай на пустое поле. Неверно. Неверно. Нeвeрнo. Задание выполнено.
Выберите верное числовое выражение.
1) 174 – 85 2) 163 – 85 3) 60 + 19 Неверно. Не кликай на пустое поле. Неверно. Неверно. 348 + 73 – 148 =
1) 200 + 73 2) 422 – 148 3) 431 – 148 Неверно. Не кликай на пустое поле. 356 – ( 256 + 40 ) =
1) 356 – 295 2) 356 – 286 3) 100 – 40 Неверно. Неверно. Неверно. Не кликай на пустое поле. Неверно. Неверно. 260 – 48 – 52 =
1) 202 – 52 2) 211 – 52 3) 260 – 100 Неверно. Не кликай на пустое поле. Неверно. Неверно. 350 – 36 – 14 =
1) 315 – 14 2) 350 – 50 3) 304 – 14 Неверно. Не кликай на пустое поле. Неверно. Нeвeрнo. Задание выполнено. Неверно.
Это интересно:
- Постановление правительства рф о негосударственной экспертизе Постановление правительства рф о негосударственной экспертизе
Личный кабинет заявителя временно недоступен.
С 01.07.2018 подача заявки на проведение негосударственной экспертизы будет осуществляться только в электронном виде через личный кабинет заявителя на сайте Негосударственной […] - Субсидии малому бизнесу челябинской области Субсидии малому бизнесу челябинской области
В ответ на Ваши обращения, поступившие на сайт «Экономика Челябинской области», сообщаем следующее.
1. На региональном уровне уполномоченным органом по вопросам, касающимся предоставления государственных услуг по содействию самозанятости […] - Принят ли закон о тунеядстве в россии Закон о тунеядстве в россии 2018 принят или нет
Сумма на в России в 2018 году Что предоставляет собой данная легитимная корректировка?
Последние новости про на в России 2018 и его сумма Минтруд предлагает ввести в России на 2018.
Максим Тополин, занимающий пост главы Министерства труда […] - Суды города сумы Теги > Заречный районный суд г. Сумы
В суде провели день открытых дверей для младших школьников
В очередной раз Заречный районный суд. Сумы стал не только местом, где вершится правосудие, но и площадкой для очередной экскурсии.
В Сумах будут рассматривать отмену 4 гривен в […] - Брежнева и развод с мужем Правда о разводе Веры Брежневой и Константина Меладзе: мнение экстрасенса
Недавно в сети прокатилась волна новостей о том, что Вера Брежнева и Константин Меладзе разводятся. Поклонники начали бить тревогу по этому поводу, поэтому появилась надобность разъяснить ситуацию. Поэтому […] - Закон рф об образовании ст 50 Главная | Закон РФ «Об образовании» | Статья 50. Права и социальная поддержка обучающихся, воспитанников
Статья 50. Права и социальная поддержка обучающихся, воспитанников
(в ред. Федерального закона от 22.08.2004 N 122-ФЗ)
(см. текст в предыдущей редакции)
1. Права и обязанности […] - Сколько статьей в ук рф Уголовный кодекс Российской Федерации
Уголовный кодекс РФ от 13 июня 1996 г. N 63-ФЗ (внесены правки от 27 мая, 25 июня 1998 г., 9 февраля, 15, 18 марта, 9 июля 1999 г., 9, 20 марта, 19 июня, 7 августа, 17 ноября, 29 декабря 2001 г., 4, 14 марта, 7 мая, 25 июня, 24, 25 июля, 31 октября […] - Ходатайство о восстановлении срока коап Примерная форма ходатайства о восстановлении срока обжалования постановления по делу об административном правонарушении (подготовлено экспертами компании «Гарант»)
Настоящая форма разработана в соответствии со ст. 30.3 КоАП РФ.
В [ наименование суда/органа, в который
[ Ф. И. О. […]
Содержание материала
- Предварительный просмотр:
- Видео
- Нахождение неизвестного множителя
- Поиск вычитаемого
- Правила нахождения уменьшаемого
- Свойства сложения
- Общие правила
- Другие методы
- Сложение в столбик многозначных чисел
Предварительный просмотр:
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Видео
Нахождение неизвестного множителя
Посмотрим на два уравнения: x·2=20 и 3·x=12. В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a·b=c при a и b, не равных , c: a=b, c: b=c и наоборот.
Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2. Проводим деление натуральных чисел и получаем 10. Запишем последовательность равенств:
x·2=20x=20:2x=10.
Подставляем десятку в исходное равенство и получаем, что 2·10=20. Значение неизвестного множителя было выполнено правильно.
Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x·=11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.
Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.
Поиск вычитаемого
Нахождение вычитаемого — это такой же простой процесс, как и поиск уменьшаемого. Уравнение может иметь следующий вид: 7-x=3. Мы имеем разность — результат вычитания, и уменьшаемое число. Формулировка правила: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Так, если мы вычитаем из одного числа неизвестное число и получаем определённый результат (разность), значит, для поиска неизвестного вычитаемого вычтем из известного числа разность. В нашем примере x=7−3, результат равен 4. Для проверки вычтем 4 из 7, и получим 3 — решение верное. Ещё один вариант проверки — сложить 3 и 4. Так как сумма равна 7, решение правильное.
Правила нахождения уменьшаемого

При поиске уменьшаемого уравнение может выглядеть следующим образом: x-2=4. Мы имеем разность — результат вычитания и число, которое вычитаем. Необходимо найти уменьшаемое — самое большое число в примере. Формулировка правила: чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Так, если мы вычитаем из неизвестного числа другое число и получаем результат, известный нам, то для поиска уменьшаемого необходимо сложить разность и вычитаемое. Простейший пример: дома были конфеты. Их количество мы не знаем. После того как Дима съел 2 конфеты, их осталось 4. Вопрос: сколько их всего было изначально? Для того чтобы узнать, прибавим 2 к 4 и получим результат — было 6 конфет. Для проверки вычтем 2 из 6. Получим результат 4 — решение верное.
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Общие правила
Для того чтобы гораздо быстрее решать элементарные уравнения, необходимо знать некоторые правила математики и логики. Здесь даже навыки арифметики не имеют такого решающего значения, как понимание того, что именно необходимо находить.
В случае с неизвестным слагаемым оно находится очень просто. От перестановки слагаемых сумма не меняется. То есть совершенно неважно, какой вид имеет уравнение x+2=6, или 2+x=6. В любом случае компонент x будет равен 4.

Дело в том, что уравнения с одним неизвестным предусмотрены школьной программой третьего класса. А ученики могут путаться и испытывать трудности в их решении, не зная этого правила.
Первое, с чего стоит начинать развитие навыка решения — это многократное повторение. Достаточно решать 5—10 уравнений в день с одним неизвестным компонентом, и уже через несколько дней ученик будет справляться с подобными заданиями гораздо быстрее. И только потом можно переходить к более сложным заданиям.

А также для улучшения понимания необходимо решать обратные уравнения. Что это значит? Вычитание — процесс, обратный сложению. То есть при сложении 3 и 4 сумма равна 7. А при вычитании 4 из 7 разность равна 3. В первом уравнении можно искать неизвестные слагаемые. При этом решать его с теми же числами, но на поиск уменьшаемого или вычитаемого.
Решение подобных уравнений точно не навредит ученику, это лишь ускорит процесс формирования навыка. При проверке и решении обратных уравнений в голове откладывается взаимосвязь между всеми компонентами примеров, а их решение практически доводит до автоматизма. Главное — постоянно тренировать этот навык.
Другие методы
Правило, которое позволяет быстро найти неизвестное слагаемое, довольно простое. Однако для того, чтобы облегчить его понимание, из него можно вывести правила, связанные с вычитанием.
Так, в примерах со сложением мы имеем два слагаемых и сумму: 3+5=8. Здесь 3 и 5 — слагаемые, а 8 — сумма. А в примерах с вычитанием мы имеем:
- Уменьшаемое.
- Вычитаемое.
- Разность.
Например, 7 — 4=3. В этом случае уменьшаемое — 7, вычитаемое — 3, а разность — 4. Уменьшаемое и вычитаемое также могут быть неизвестными. И крайне важно знать, как их вычислять.
Сложение в столбик многозначных чисел
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Итак, допустим, что нам нужно найти сумму : 5728+803


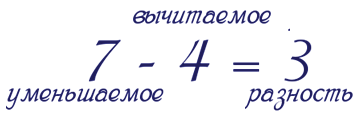



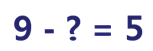





 Разность чисел означает, насколько одно из них больше другого.
Разность чисел означает, насколько одно из них больше другого.





