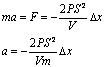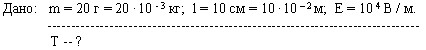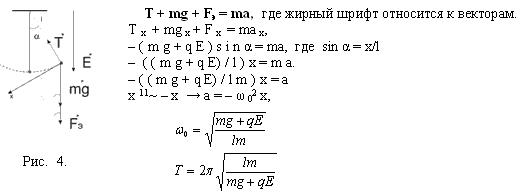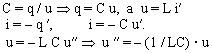Как найти период малых колебаний шарика - AvtoShod.ru

Найти период малых вертикальных колебаний шарика на натянутой струне

Опубликовано сб, 09/21/2019 — 20:53 пользователем fizportal.ru

4.18. Найти период малых вертикальных колебаний шарика массы $m = 40$ г, укрепленного на середине горизонтально натянутой струны длины $l = 1,0$ м. Натяжение струны считать постоянным и равным $F = 20$ Н.

Решение:

Расставим силы, действующие на шарик при малом отклонении $x$ вниз (рис.)

$ma = mfrac{d^2x}{dt^2} = mg – 2Fsintheta$,

Так как отклонения малые, то справедливо равенство для малых углов

$sintheta approx theta$

тогда

$ma = mfrac{d^2x}{dt^2} = mg – 2Ftheta$. (1)

Из геометрии рисунка

$theta approx frac{x}{l/2}$.

Перепишем уравнение (1)

$mfrac{d^2x}{dt^2} = mg – 2Ffrac{x}{l/2} = mg – 4Ffrac{x}{l}$.

Или

$frac{d^2x}{dt^2} = g – 4Ffrac{x}{ml} approx -frac{4F}{ml}(x — mgfrac{l}{4F})$.

Откуда

$omega^2 = frac{4F}{ml}$,

а с учетом того, что

$omega = frac{2pi}{T}$,

получаем

$T = pi sqrt frac{ml}{F}$.

Ответ: $T = pi sqrt frac{ml}{F}$.

Источник

Решение. Шарик подвешен на нити будем считать математическим маятником.
Период колебаний математического маятника определяется по формуле:

[ T=2cdot pi cdot sqrt{frac{A}{g}} (1). ]

Математический маятник находится в поле действия нескольких сил. Силы тяжести и силы Архимеда.
g – эффективное ускорение, характеризующее результирующее действие этих сил.
Силы направлены в противоположные стороны:

[ vec{g}={{vec{g}}_{0}}+vec{a} (2). ]

g₀ – ускорение свободного падения, g₀ = 10 м/с².
Определим а. Покажем рисунок.

[ begin{align}
& vec{g}={{{vec{g}}}_{0}}+vec{a}. \
& oY: g={{g}_{0}}-frac{{{rho }_{1}}cdot {{g}_{0}}cdot V}{m}, V=frac{m}{rho }, g={{g}_{0}}-frac{{{rho }_{1}}cdot {{g}_{0}}cdot m}{mcdot rho }, g={{g}_{0}}-frac{{{rho }_{1}}cdot {{g}_{0}}}{rho }, \
& frac{{{rho }_{1}}}{rho }=frac{1}{3}, g={{g}_{0}}-frac{1cdot {{g}_{0}}}{3}, g=frac{2cdot {{g}_{0}}}{3} (3). \
end{align}
]

Подставим (3) в (2)

[ T=2cdot pi cdot sqrt{frac{3cdot A}{2cdot {{g}_{0}}}} (4). ]

Т = 1,0 с.

« Последнее редактирование: 15 Февраля 2015, 07:12 от alsak »

Записан

Источник

Механические колебания.

Гармонические колебания.
Уравнение гармонических колебаний.
Пружинный маятник.
Математический маятник.
Свободные и вынужденные колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: nu =1/T . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

к оглавлению ▴

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение x=0 . Основная задача механики в данном случае состоит в нахождении функции x(t) , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на pi /2 , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина alpha , равная значению фазы при t=0 , называется начальной фазой. Начальная фаза отвечает начальной координате тела: $x_{0}=Acos alpha$ .

Величина называется omega циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное 2 pi радиан: , откуда

$omega = frac{displaystyle 2pi }{displaystyle T}$ (2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

$x=Acos(frac{displaystyle 2pi t }{displaystyle T}+ alpha), x=Acos(2 pi nu t + alpha)$ .

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину $x_{0}$ и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае $x_{0}=A$ , поэтому можно положить alpha=0 . Мы получаем закон косинуса:

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае $x_{0}=0$ , так что можно положить . Получаем закон синуса:

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

к оглавлению ▴

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

$v_{x}=dot{x}=-Aomega sin(omega t+alpha )$ . (4)

Теперь дифференцируем полученное равенство (4):

$a_{x}=ddot{x}=-Aomega^{2} cos(omega t+alpha )$ . (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем $-omega^{2}$ :

$a_{x}=-omega^{2}x$ . (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

$ddot{x}+omega^{2}x=0$ . (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой omega и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

к оглавлению ▴

Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате x=0 отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости vec F со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

$ma_{x}=F_{x}$ . (8)

Если x>0 (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и $F_{x}<0$ . Наоборот, если x<0 , то $F_{x}>0$ . Знаки и $F_{x}$ всё время противоположны, поэтому закон Гука можно записать так:

$F_{x}=-kx$

Тогда соотношение (8) принимает вид:

$ma_{x}=-kx$

или

$a_{x}=-frac{displaystyle k}{displaystyle m}x$ .

Мы получили уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle k}{displaystyle m}$ .

Циклическая частота колебаний пружинного маятника, таким образом, равна:

$omega =sqrt{frac{displaystyle k}{displaystyle m}}$ . (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

$T=2 pi sqrt{frac{displaystyle m}{displaystyle k}}$ . (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

к оглавлению ▴

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

$ma_{x}=T_{x}$ .

Если маятник занимает положение как на рисунке (т. е. x>0 ), то:

$T_{x}=-Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Если же маятник находится по другую сторону от положения равновесия (т. е. x<0 ), то:

$T_{x}=Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Итак, при любом положении маятника имеем:

$ma_{x}=-Tfrac{displaystyle x}{displaystyle l}$ . (11)

Когда маятник покоится в положении равновесия, выполнено равенство T=mg . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

$ma_{x}=-mgfrac{displaystyle x}{displaystyle l}$ ,

или

$a_{x}=-frac{displaystyle g}{displaystyle l}x$ .

Это — уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle g}{displaystyle l}$ .

Следовательно, циклическая частота колебаний математического маятника равна:

$omega =sqrt{frac{displaystyle g}{displaystyle l}}$ . (12)

Отсюда период колебаний математического маятника:

$T=2pi sqrt{frac{displaystyle l}{displaystyle g}}$ . (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

к оглавлению ▴

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы F(t) , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна $omega_{0}$ , а вынуждающая сила зависит от времени по гармоническому закону:

$F(t)=F_{0}cos omega t$ .

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
omega вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

Мы видим, что вблизи частоты $omega=omega_{r}$ наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: $omega_{r} approx omega_{0}$ , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, $omega_{r} = omega_{0}$ , а амплитуда колебаний возрастает до бесконечности при $omega Rightarrow omega_{0}$ .

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Рассмотрим теперь единый подход к решению задач на расчет периода различных видов колебаний.

Например, колебания совершают различные маятники, струны музыкальных инструментов, молекулы газа в звуковых волнах и молекулы жидкости в морских волнах. Колебания совершают атомы в твердых телах и электроны, входящие в состав атомов. Колебания заряда и тока происходят в колебательных контурах радиоприемников и телевизоров. По таким же законам происходят изменения напряженности электрического поля и индукции магнитного поля в электромагнитной волне.

Главное заключается в том, что все эти различные физические явления описываются одинаковыми математическими уравнениями, то есть подчиняются одинаковым законам.

Рассмотрим решения задач на различные виды свободных колебаний. Потери энергии в таких колебательных системах пренебрежимо малы.

В механике.

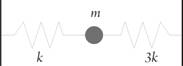
Задача 1. Шарик присоединен к двум пружинам так, как изображено на рисунке. Масса шарика равна m, жесткость одной пружины равна k, жесткость другой – 3k. Определите период малых колебаний шарика T.

Рис. 1.

Если шарик сдвинуть на расстояние x от положения равновесия, то согласно второму закону Ньютона m a = – k x – 3 k x = – 4 k x, откуда находим a = – ( 4 k / m ) x или x″= – (4 k/m) x.

Сравнивая это уравнение с уравнением колебаний x″ = – ω² x, получаем:

Период колебаний:

В молекулярной физике.

Задача 2. В сосуде, разделенном подвижным поршнем массой m и площадью поперечного сечения S, находится идеальный газ. Когда поршень расположен ровно посередине сосуда, давление газа в каждой половине p, объем половины сосуда равен V. Определите период малых колебаний поршня, считая процесс колебаний изотермическим, трением пренебречь.

Объем каждой из частей , ,

значит,

откуда получаем значение силы

Так как ∆ х < V / S, то

Согласно второму закону Ньютона получим:

где а – ускорение поршня.

т. е. х ´´ ~ – x , а это значит, что «х» изменяется по законам синуса или косинуса и
a = x “ = – ω0 2 x. Поэтому

Рис. 3.

В электростатике.

Задача 3. Шарик массой m = 20 г подвешен на шелковой нити длиной l = 10 см. Шарик имеет положительный заряд q = + 10^–5 Кл и находится в однородном электрическом поле напряженностью Е = 10⁴ В / м, направленном вертикально вниз. Каков период малых колебаний шарика?

Отведем заряженный шарик, находящийся в электрическом поле на малый угол α. Показываем силы на него действующие.Применяем второй закон Ньютона, учитывая, что сила, возвращающая заряженный шарик в положение равновесия и угол отклонения шарика из положения равновесия имеют противоположное направление – это означает знак «–».

Задача 4. Колебательный контур, состоящий из конденсатора емкостью С и катушки индуктивностью L, подключен через ключ К к источнику с постоянной ЭДС ε и внутренним сопротивлением r (рис. 5).

Рис. 5.

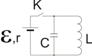
Ключ замыкают, а после того как устанавливается постоянный режим, размыкают его. Найти зависимость напряжения на конденсаторе от времени после размыкания ключа. Омическим сопротивлением катушки пренебречь.

При замкнутом ключе через катушку течет постоянный ток I = ε / r. Напряжение на конденсаторе и заряд на нем равны нулю, так как напряжение на конденсаторе равно напряжению на катушке, а оно, при отсутствии активного сопротивления катушки, равно нулю. Из начальных условий t = 0 u = 0 и i = ε / r следует, что напряжение на конденсаторе в зависимости от времени изменяется по закону синуса

После размыкания ключа в колебательном контуре начнутся свободные электромагнитные колебания. Пусть в некоторый момент времени заряд на конденсаторе q, а напряжение на конденсаторе равно u. Напряжение на катушке будет тоже u.

Это означает, что напряжение изменяется по гармоническому закону, а уравнение

, а амплитуда напряжения

Зависимость напряжения на конденсаторе от времени после размыкания ключа имеет вид

Задачи для самостоятельного решения.

1. Шарик массой m = 20 г, подвешен на шелковой нити и помещен над положительно заряженной плоскостью, создающей вертикальное однородное электрическое поле напряженностью. Шарик имеет положительный заряд Кл. Период малых колебаний шарика Т = 1 с. Чему равна длина нити?

2. При отклонении из положения равновесия ареометр в сосуде с водой совершает гармонические колебания с периодом 1 с. Каков будет период колебаний ареометра в керосине? Сопротивлением среды пренебречь. (1, 12 с )

3. Маятник с периодом колебаний 1 с представляет собой шарик массой 16 г, подвешенный на нити, не проводящей электричество. Шарик электризуют отрицательным зарядом и помещают в электрическое поле, Период колебаний маятника Т1 = 0, 95 с. Вычислить напряженность электрического поля, если заряд на шарике равен Кл. (В/м )

4. В колебательном контуре, состоящем из катушки индуктивности и воздушного конденсатора, величина тока меняется со временем по гармоническому закону: i = I м cos ω t . Когда ток контуре оказывается равным нулю, в пространство между пластинами конденсатора быстро вводят диэлектрическую пластину с диэлектрической проницаемостью ε. Время этого внешнего воздействия мало по сравнению с периодом колебаний в контуре. Найдите зависимость тока в контуре от времени после внесения пластины.

Такой подход к обучению поможет обучающимся быть более уверенными в себе при решении задач на нахождение периода гармонических колебаний. Эта информация обеспечит понимание применения метода аналогий в решении задач на различные виды колебаний.

Литература

Лабковский, В.Б. 220 задач по физике с решениями: кн. для учащихся 10 –11 кл. общеобразоват. учреждений / В.Б. Лабковский. – М. : Просвещение, 2006. –256 с. :ил. – (Задачник).
Гомонова, А.И., Плетюшкин, В.А., Погожев В.А. Задачи по физике. Пособие для учащихся 9-11 классов. – М.: Экзамен (Серия «Экзамен»), 1998. – 192 с.
Панов, Н.А., Шабунин, С.А., Тихонин, Ф.Ф. Единый государственный экзамен. Физика. Типовые тестовые задания: Учебно-практическое пособие / Н.А. Панов, С.А. Шабунин, Ф.Ф. Тихонин. – М.: Издательство «Экзамен», 2003. – 56 с.
Орлов, В.А., Никифоров, Г.Г., Ханнанов, Н.К. Учебно-тренировочные материалы для подготовки к единому государственному экзамену. Физика / Орлов В.А., Никифоров Г.Г., Ханнанов Н.К. – М.: Интеллект-Центр, 2005 –248 с.

Источник

2018-05-31

Найти период малых вертикальных колебаний шарика массы $m = 40 г$, укрепленного на середине горизонтально натянутой струны длины $l = 1,0 м$. Натяжение струны считать постоянным и равным $F = 10 Н$.

Решение:

Расположим и покажем силы, действующие на шар, в положении, когда оно находится на расстоянии x от недеформированного положения струны.

В этом положении неуравновешенная сила, приложенная к шару, направленна вниз

$= mg — 2F sin theta$

По закону Ньютона $m ddot{x} = mg — 2 F sin theta$

$= mg — 2F theta$ (когда $theta$ мало)

$= mg — 2F frac{x}{l/2} = mg — frac{2F}{l} x$

Таким образом, $ddot{x} = g — frac{4F}{ml}x = — frac{2F}{ml} left ( x — frac{mgl}{4F} right )$

Подставляя $x^{ prime} = x — frac{mgl}{T}$, мы получаем

$ddot{x}^{ prime} = — frac{4T}{ml}x^{ prime}$

Таким образом, $T = pi sqrt{ frac{ml}{F} } = 0,2 с$

Источник

Найти период малых вертикальных колебаний шарика на натянутой струне

Механические колебания.

Гармонические колебания.

Уравнение гармонических колебаний.

Пружинный маятник.

Математический маятник.

Свободные и вынужденные колебания.

Не пропустите также: