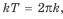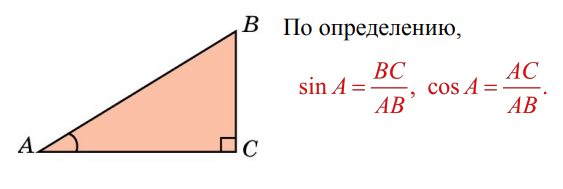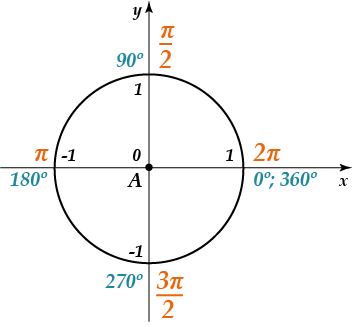Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции 
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции 
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции 
. Это можно записать так:
.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции


Синус — нечетная функция: 
Синус — периодическая функция с наименьшим положительным периодом :

вид графика функции

, а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние
, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение
. Тогда соответствующее значение
, то есть график функции
проходит через начало координат.
На оси значение

, при которых


Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, 


Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому 

Промежутки возрастания и убывания. Учитывая периодичность функции 



Если 




Рис.2 Рис.3
Если 




Проведенное исследование позволяет обоснованно построить график функции 







Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной 


на

Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой 
График функции 

. Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой

колебания, 


СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число)
.
- Область значений:
-
Функция четная:
(график симметричен относительно оси
).
- Функция периодическая с периодом
:
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции 

Рис.7
Для точек единичной окружности абсциссы находятся в промежутке 

точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции 

Как видим, наибольшее значение функции 

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при 
Косинус — четная функция: 

Косинус — периодическая функция с наименьшим положительным периодом 



Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси 







Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 


Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому 
Промежутки возрастания и убывания. Учитывая периодичность функции 


Если 





Если 





Рис.8 Рис.9
Проведенное исследование позволяет построить график функции 
. Но график функции


Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки 
абсциссы и ординаты этих точек. Так как 
прямоугольника 



Укажем также формулы, которые нам понадобятся далее:
Тогда,
Таким образом, 
Учитывая, что 

его параллельным переносом вдоль оси


Рис.11
Рис.12
СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции 
Свойства функции 
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
СВОЙСТВО ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
На этой странице вы узнаете
- Как найти углы у апельсина?
- Кто сказал “Ты как хочешь, а я уехала!”
Люди пользуются тригонометрией с древнейших времен. Добывая еду с помощью лука и стрел, человек уже применял знания, которые мы разберем в этой статье.

Единичная тригонометрическая окружность
Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1
Так как длина всей окружности равна 2π, сделаем вывод, что половина окружности — это π, а четверть — это π2.

Теперь разделим окружность сначала на восемь частей, а потом ту же окружность на двенадцать частей. Рассчитаем значения полученных точек.

Заметим, что точка 0 совпадает с точкой 2π. Это означает, что мы сделали один оборот по окружности. Но мы можем продолжать идти так и дальше: тогда эта же точка будет принимать значения 4π, 6π, 8π.
Для удобства представим, что окружность — это половинка апельсина. Длина корочки апельсина равна 2π. А теперь будем делить 2π на 4, 8 и 12. Таким образом, получившиеся кусочки апельсина будут являться углами на тригонометрической окружности.

Движение по тригонометрической окружности можно сравнить с движением по числовой прямой, закрученной в спираль.

Аналогично можно двигаться и против движения часовой стрелки, но это уже будет отрицательная спираль.


Как записать множество точек, находящихся в одной точке окружности, но на разных витках спирали?
Так как тригонометрические функции — это периодические функции, то и значения в точках будут повторяться с определенным интервалом: то есть с интервалом 2πk, где k принадлежит множеству целых чисел.
Пример: π + 2πk, k ∈ Z
Теперь рассмотрим значения синусов и косинусов, определенных на окружности точек.
На положительных частях осей они представлены как (frac{1}{2}), (frac{sqrt{2}}{2}), (frac{sqrt{3}}{2}), а на отрицательных — (-frac{1}{2}), (-frac{sqrt{2}}{2}), (-frac{sqrt{3}}{2}).

Для нахождения значения синуса или косинуса известного угла нужно провести перпендикулярную прямую к прямой, предназначенной этой функции. Значение, в котором она пересечет прямую функции будет являться значением этой тригонометрической функции от известного числа.
Пример:
Нужно узнать чему равно (sin frac{pi}{3})
Сначала найдем (frac{pi}{3}) на окружности, затем проведем перпендикулярную прямую к прямой синусов. Ответом является значение в точки пересечения.

(sin frac{pi}{3} = frac{sqrt{3}}{2})
Теперь проведём ещё две прямые для обозначения прямых тангенса и котангенса. Отметим на них значения для точек окружности.

Для нахождения значения тангенса или котангенса известного угла нужно провести прямую через точку (0; 0) и это число на окружности. Значение, в котором она пересечет прямую данной функции, будет являться значением этой тригонометрической функции от известного числа.
Пример:
Нужно узнать чему равно (ctg frac{2 pi}{3})
Сначала найдем (frac{2 pi}{3}) на окружности, затем проведём прямую через (0; 0) и эту точку на окружности. Ответом является значение в точки пересечения проведенной прямой и прямой котангенсов.

(ctg frac{2 pi}{3} = -frac{sqrt{3}}{3})
Примеры тригонометрии можно найти и в жизни. Например: когда мы режем морковку, нож находится под углом (frac{pi}{2}) к поверхности доски.

Графики тригонометрических функций
Как уже было сказано ранее, тригонометрические функции — это периодические функции.
То есть, значения этих функций повторяются через определенный период. Теперь рассмотрим подробнее графики таких функций.
Находя значения у для разных значений х и соединяя точки, можно получить следующие графики функций.
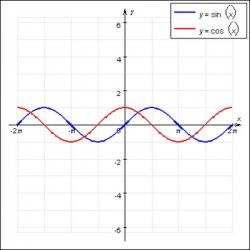
График y = sin x — синусоида.

График y = cos x — косинусоида.

График y = tgx — тангенсоида.

Важно: тангенсоида никогда не может принимать значения (frac{pi}{2}); (frac{3 pi}{2}); (frac{5 pi}{2}) и т. д. Так как тангенс — это синус делить на косинус, а делить на ноль нельзя, следовательно, косинус не равен нулю. Данные значения отмечены на графике пунктирными линиями.
График y = ctgx — котангенсоида.

Важно: котангенсоида никогда не может принимать значения 0; π; 2π и т. д., так как котангенс — это косинус делить на синус. Делить на ноль нельзя, значит синус не равен нулю. Данные значения отмечены на графике пунктирными линиями.
Каждую из рассмотренных выше функций можно сдвигать по осям Х и Y и растягивать по оси Y. Давайте рассмотрим такие растяжения и сдвиги.
Коэффициент перед тригонометрической функцией
Чем больше коэффициент перед тригонометрической функцией, тем сильнее она вытягивается по вертикали.
Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида растягиваются по аналогии.


Сдвиг по оси Y
График тригонометрической функции сдвигается по оси Y на прибавленную к значению y константу.
Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида сдвигаются по аналогии.


Сдвиг по оси Х
График тригонометрической функции сдвигается по оси Х на прибавленную к значению х константу.
Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида сдвигаются по аналогии.
Важно: при прибавлении положительной константы — сдвиг влево, при вычитании положительной константы — сдвиг вправо.


Косинусоида, она такая. Сказала — и подвинулась на 2 вверх и вправо. Как она это сделала?
Рассмотрим сдвиг косинусоиды по двум осям сразу
Изначальный вид функции: y=cos x
Сдвиг на 2 вверх: y = cos x + 2
Сдвиг на вправо: y = cos(x — π) + 2
Получилось, что функция косинусоиды после сдвигов — это y=cos(x — π) + 2
Фактчек
- Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1.
- Один проход по окружности — это 2π.
- Двигаться по окружности можно как в положительную, так и в отрицательную сторону.
- График функции — это представление функции на координатной плоскости.
- Коэффициент перед функцией отвечает за растяжение графика функции вдоль оси Y.
- Константа, прибавляемая к х или y, отвечает за сдвиг функции относительно изначального значения.
Проверь себя
Задание 1.
Чему равно (sin frac{5 pi}{4})?
- (frac{sqrt{3}}{2})
- (frac{sqrt{2}}{2})
- (-frac{sqrt{2}}{2})
- 1
Задание 2.
Чему равно (cos frac{pi}{3})?
- 1
- (frac{1}{2})
- (-frac{1}{2})
- (frac{sqrt{3}}{2})
Задание 3.
Чему равно (ctg frac{pi}{2})?
- 0
- 1
- (sqrt{3})
- (frac{sqrt{2}}{2})
Задание 4.
Куда будет сдвиг (sin(x + frac{4 pi}{3}))?
- Вправо
- Влево
- Вверх
- Вниз
Задание 5.
Куда будет сдвиг ctg x + 2?
- Вправо
- Влево
- Вниз
- Вверх
Ответы: 1. — 3; 2. — 2; 3. — 1; 4. — 2; 5. — 4.
Как найти период тригонометрической функции
Тригонометрические функции периодичны, то есть повторяются через определенный период. Благодаря этому достаточно исследовать функцию на этом промежутке и распространить найденные свойства на все остальные периоды.
Инструкция
Если вам дано простое выражение, в котором присутствует лишь одна тригонометрическая функция (sin, cos, tg, ctg, sec, cosec), причем угол внутри функции не умножен на какое-либо число, а она сама не возведена в какую-либо степень – воспользуйтесь определением. Для выражений, содержащих sin, cos, sec, cosec смело ставьте период 2П, а если в уравнении есть tg, ctg – то П. Например, для функции у=2 sinх+5 период будет равен 2П.
Если угол х под знаком тригонометрической функции умножен на какое-либо число, то, чтобы найти период данной функции, разделите стандартный период на это число. Например, вам дана функция у= sin 5х. Стандартный период для синуса – 2П, разделив его на 5, вы получите 2П/5 – это и есть искомый период данного выражения.
Чтобы найти период тригонометрической функции, возведенной в степень, оцените четность степени. Для четной степени уменьшите стандартный период в два раза. Например, если вам дана функция у=3 cos^2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите внимание, функции tg, ctg в любой степени периодичны П.
Если вам дано уравнение, содержащее произведение или частное двух тригонометрических функций, сначала найдите период для каждой из них отдельно. Затем найдите минимальное число, которое умещало бы в себе целое количество обоих периодов. Например, дана функция у=tgx*cos5x. Для тангенса период П, для косинуса 5х – период 2П/5. Минимальное число, в которое можно уместить оба этих периода, это 2П, таким образом, искомый период – 2П.
Если вы затрудняетесь действовать предложенным образом или сомневаетесь в ответе, попытайтесь действовать по определению. Возьмите в качестве периода функции Т, он больше нуля. Подставьте в уравнение вместо х выражение (х+Т) и решите полученное равенство, как если бы Т было параметром или числом. В результате вы найдете значение тригонометрической функции и сможете подобрать минимальный период. Например, в результате упрощения у вас получилось тождество sin (Т/2)=0. Минимальное значение Т, при котором оно выполняется, равно 2П, это и будет ответ задачи.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
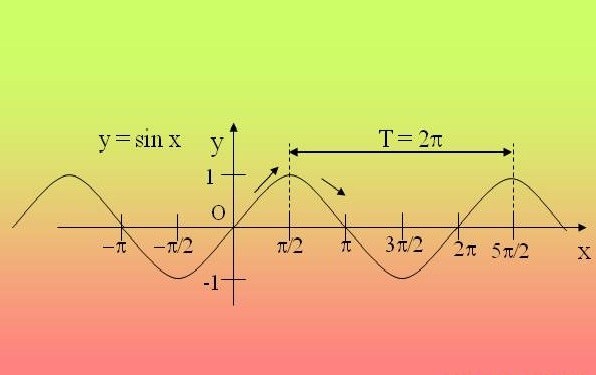
Как определить период по графику
Многие математические функции имеют одну особенность, облегчающую их построение, — это периодичность, то есть повторяемость графика на координатной сетке через равные промежутки.
Самыми известными периодическими функциями математики являются синусоида и косинусоида. Эти функции имеют волнообразный характер и основной период, равный 2П. Также частным случаем периодической функции является f(x)=const. На позицию х подходит любое число, основного периода данная функция не имеет, так как представляет собой прямую.
Вообще функция является периодической, если существует такое целое число N, которое отлично от нуля и удовлетворяет правилу f(x)=f(x+N), таким образом обеспечивая повторяемость. Период функции — это и есть наименьшее число N, но не ноль. То есть, например, функция sin x равна функции sin (x+2ПN), где N=±1, ±2 и т.д.
Иногда при функции может стоять множитель (например sin 2x), который увеличит или сократит период функции. Для того чтобы найти период по , необходимо определить экстремумы функции — самую высокую и самую низкую точки графика функции. Так как синусоида и косинусоида имеют волнообразный характер, это достаточно легко сделать. От данных точек постройте перпендикулярные прямые до пересечения с осью Х.
Расстояние от верхнего экстремума до нижнего будет половиной периода функции. Удобнее всего вычислять период от пересечения графика с осью Y и, соответственно, нулевой отметки по оси х. После этого необходимо умножить полученное значение на два и получить основной период функции.
Для простоты построения графиков синусоиды и косинусоиды необходимо отметить, что если при функции стоит целое число, то ее период удлинится (то есть 2П необходимо умножить на этот коэффициент) и график будет выглядеть более мягко, плавно; а если число дробное, наоборот, сократится и график станет более «острым», скачкообразным на вид.
Определения
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.
Синус угла А обозначается sin A.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
Косинус угла А обозначается cos A.
Наглядно это видно на следующем рисунке:
Функция косинуса: свойства и значения функции косинус
Определение
Функцией косинуса называют элементарную тригонометрическую функцию, выражающую зависимость угла при вершине треугольника от отношения прилежащей его стороны к гипотенузе.
- Основные свойства функции косинус следующие:
- Область определения функции косинуса (значений, которые может принимать аргумент x) – множество всех действительных чисел;
- Значения функции косинус – это (+1) и (-1) и множество действительных чисел между ними.
- Наименьшее значение функции косинус равно 1, а наибольшее – (-1);
- Функция чётная, т. е. cos(-x) = cos(x);
- Функция периодическая. Её период равен 2π;
- Наибольшего своего значения функция косинус x достигает в точках x=2πk;
- Наименьшее значение функции косинус x будет в точках x= π/2+2πk;
- Область возрастания функции cos(x): -π+2πk<=x<=2πk;
- Область убывания функции cos(x): 2πk<= π+2πk;
- Функция не имеет разрывов, т. е. непрерывна.
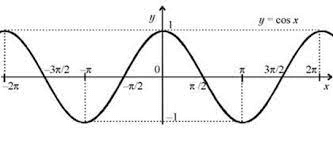
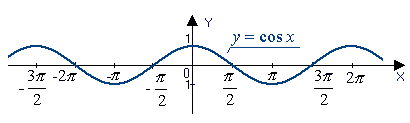
График функции косинус
Графиком функции является косинусоида. Он получается из графика синуса с помощью параллельного переноса на расстояние [frac{pi}{2}] влево. Он выглядит следующим образом:
Как построить график функции косинус икс
График функции косинуса можно построить следующим образом:
Используем данные единичной окружности, приведённой на рисунке выше.
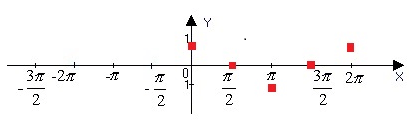
Из рисунка единичной окружности видно, что в точке ноль ордината функции равна единице. В точке π/2 по оси X значение Y равно 0. В точке π по оси X ордината равна (-1). В точке 3π/2 значение функции снова равно 0, а в точке 2π значение по оси X равно 1. Отметим все названные точки.
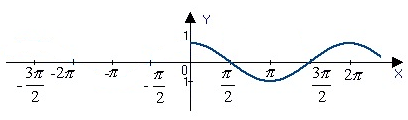
Соединим их плавной линией
Т. к. наша функция чётная (свойство №4), её график симметричен оси Y. Зеркально отразим его. Помимо этого нам известно, что период функции равен 2π. Из данного свойства следует неограниченная повторяемость кусочка функции между 0 и 2π в обе стороны вдоль оси X. График функции косинус x построен.
Нет времени решать самому?
Наши эксперты помогут!
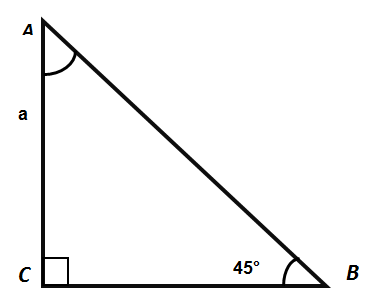
Как найти значение функции косинуса при x равном 45 градусам
Построим прямоугольный треугольник с катетами, равняющимися единице. Сумма углов любого треугольника, как известно, равна 180 градусам. Если вычтем из них прямой угол, получим сумму двух оставшихся углов. Это углы при вершинах A и B. Так как катеты равны, то и выше названные углы равны и каждый из них составляет (180 – 90)/2 = 45 градусов.
По теореме Пифагора гипотенуза его в этом случае будет равна [c=sqrt{a^{2}+a^{2}}=sqrt{1+1}=sqrt{2}]
Из определения косинуса находим [cos (a)=1 / sqrt{2}]
После вычисления и округления числа получим 0,7071. Это и есть косинус 45 градусов.

![file.[2]](https://ya-znau.ru/information/userfiles/73/file.%5B2%5D.jpg)
![file.[3]](https://ya-znau.ru/information/userfiles/73/file.%5B3%5D.jpg)

![file.[4]](https://ya-znau.ru/information/userfiles/73/file.%5B4%5D.jpg)