Как найти период колебаний
Для нахождения периода колебаний возьмите время, за которое произошло некоторое количество колебаний и поделите на это количество. Для определения периода колебаний математического маятника измерьте его длину и рассчитайте период. Для пружинного маятника определите его жесткость и массу груза. Чтобы определить период электромагнитных колебаний, найдите емкость и индуктивность контура.

Вам понадобится
- секундомер, пружинный и математический маятник, катушка и конденсатор.
Инструкция
Простейший способ определения периода колебаний Возьмите секундомер и включив его, отсчитайте некоторое количество колебаний. Как правило, прлучается от 10 до 30 штук. Затем время в секундах, за которое произошли эти колебания, поделите на их количество. В результате получите значение периода в секундах.
Определение периода колебаний математического маятника Возьмите математический маятник (малое тело на длинной нити) и измерьте длину нити в метрах. Затем длину это значение поделите на число 9,81 из результата извлеките квадратный корень, а получившееся число умножьте на число 6,28. Это и будет периодом колебаний математического маятника.
Определение периода колебаний пружинного маятника Измерьте массу груза, который будет колебаться на пружине. Затем узнайте жесткость пружины. Если она не известна, возьмите груз и с помощью динамометра определите его вес (в неподвижном состоянии он будет равен силе тяжести), затем подвесьте на пружину и с помощью линейки найдите ее удлинение в метрах. Затем вес тела поделите на удлинение пружины и получите ее жесткость в ньютонах на метр. Чтобы найти период колебаний пружинного маятника, массу груза поделите на жесткость пружины, из полученного числа извлеките квадратный корень и умножьте его на 6,28.
Определение периода электромагнитных колебаний Для этого найдите индуктивность катушки и емкость конденсатора в колебательном контуре. Если они не известны, примените электронный тестер, задав соответствующие настройки. Индуктивность измеряйте в генри, а емкость в фарадах. После этого перемножьте полученные значения индуктивности и емкости, извлеките из числа квадратный корень, а результат умножьте на 6,28.
Видео по теме
Полезный совет
Во всех случаях, когда известна частота колебаний, для того чтобы найти их период, достаточно число 1 поделить на значение частоты.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
В первой части нашей работы мы должны будем с вами с
помощью экспериментальной установки исследовать зависимость периода свободных
колебаний нитяного маятника от его длины.
Для выполнения этой работы нам предлагается использовать
оборудование из комплекта № 5 в составе: штатив с муфтой и креплением для нити,
груз с крючком, нить, электронный секундомер и метровую линейку или мерную
ленту.
Прежде чем приступить к работе давайте с вами вспомним, что маятником
называется твёрдое тело, совершающее под действием приложенных сил
колебания около неподвижной точки или вокруг оси.
Существует несколько видов маятников. Но наиболее часто
встречающиеся, это пружинный маятник, представляющий собой груз,
прикреплённый к пружине, и способный совершать колебания вдоль горизонтальной
или вертикальной оси.
И нитяной маятник — шарик, подвешенный на нити,
способный совершать колебательное движение.
Теперь давайте вспомним, что любое колебательное движение
характеризуется амплитудой, частотой и периодом колебаний.
Амплитуда колебаний — это наибольшее смещение
колеблющегося тела от положения равновесия.
Частота
колебаний — это
число колебаний, совершаемых телом за единицу времени. Обозначается она
греческой буквой ν. А единицей её измерения в системе СИ является герц
[Гц]:
И, наконец, период
колебаний — это наименьший промежуток времени, через который полностью
повторяется состояние колебательной системы. Обозначается период большой буквой
Т. Единица измерения — секунда [с]:
Ещё в
середине XVII века нидерландский учёный Христиан Гюйгенс показал, что «период малых
колебаний математического маятника зависит от длины подвеса и ничего более»:
И в первой
части нашей работы мы с вами должны будем проверить, как зависит период
колебаний маятника от его длины.
Итак, для
начала давайте соберём экспериментальную установку. Для этого закрепим
перекладину в муфте у верхнего края стержня штатива. Штатив разместим на столе
так, чтобы конец перекладины выступал за край поверхности стола. Далее подвесим
к перекладине с помощью нити груз из набора. И сразу же установим длину нити в
1 м. Электронный секундомер переведём в ручной режим работы.
Далее мы
сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с
горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого
много меньше длины нити — это положение равновесия маятника. Далее изображаем
маятник в положении максимального отклонения (не более 15° от положения
равновесия.
Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, период колебаний равен отношению промежутка времени,
в течение которого тело совершило N полных колебаний, к числу этих
колебаний:
Так как нам необходимо будет провести несколько измерений, то
давайте с вами составим таблицу. В первой колонке мы укажем номера опытов. Во
второй колонке мы запишем значения длины маятника, которые нам даны в условии
задания. Число колебаний маятника мы запишем в третью колонку (во всех опытах
оно будет одинаковым и равно 30). Четвёртую колонку мы отведём для записи
времени совершения заданного числа колебаний. А в последнюю колонку будем
записывать значения периода колебаний маятника.
Теперь приступим непосредственно к работе. Итак, отклоняем
нить маятника на угол не более 10—15° (можно помочь себе транспортиром). Затем
отпускаем груз и даём маятнику совершить два — три полных колебания, чтобы
процесс колебаний стал установившимся. В момент прохождения маятником крайнего
положения запускаем секундомер. Теперь нам остаётся только дождаться, пока
маятник не совершит 30 полных колебаний. По окончании последнего колебаний
останавливаем секундомер.
Значение промежутка времени, за которое маятник совершил
заданное число колебаний, записываем в таблицу с учётом погрешности измерения:
Теперь уменьшим длину нити маятника в два раза и повторим
эксперимент. По окончании тридцатого колебания останавливаем секундомер и
записываем значение промежутка времени в таблицу.
Наконец уменьшаем длину маятника до 25 см и, включив секундомер,
вновь отсчитываем 30 полных колебаний. Не забываем записать в таблицу значение
промежутка времени с учётом погрешности измерения:
Прямые измерения мы с вами завершили. Теперь определяем
период колебаний. Для этого подставляем в расчётную формулу значения
промежутков времени и числа полных колебаний для каждого из трёх случаев:
Теперь хорошо видно, что чем меньше длина нити маятника, тем
меньше его период колебаний. Поэтому в выводе напишем: при уменьшении
длины нити период свободных колебаний нитяного маятника уменьшается.
Во второй части работы мы с вами должны будем
проверить, зависит ли период колебаний нитяного маятника от массы груза.
Оборудование мы будем использовать практически то же самое:
штатив с муфтой и креплением для нити, набор грузов с крючками, нить,
электронный секундомер и метровую линейку или мерную ленту.
Итак, для
начала давайте соберём экспериментальную установку. Для этого закрепим
перекладину в муфте у верхнего края стержня штатива. Штатив разместим на столе
так, чтобы конец перекладины выступал за край поверхности стола. Далее подвесим
к перекладине с помощью нити один груз из набора. Длина маятника по условию
задания у нас должна быть равна 1 м. Электронный секундомер переведём в ручной
режим работы.
Далее мы
сделаем рисунок нашей установки. Для этого нарисуем сначала штатив с
горизонтальной стойкой. И «привязываем» к стойке нить с грузом, размер которого
много меньше длины нити — это положение равновесия маятника. Далее изображаем
маятник в положении максимального отклонения (не более 15° от положения
равновесия.
Теперь
запишем формулы, которыми будем пользоваться при выполнении данной работы. Как
мы уже вспоминали, период колебаний равен отношению промежутка времени,
в течение которого тело совершило N полных колебаний, к числу этих
колебаний:
Так как нам необходимо будет провести несколько измерений, то
давайте с вами составим таблицу. В первой колонке мы укажем номера опытов. Во
второй колонке мы запишем значения массы маятника, которые нам даны в условии
задания. Число колебаний маятника мы запишем в третью колонку (во всех опытах
оно будет одинаковым и равно 30). Четвёртую колонку мы отведём для записи
времени совершения заданного числа колебаний. А в последнюю колонку будем
записывать значения периода колебаний маятника.
Теперь приступим непосредственно к работе. Итак, отклоняем
нить маятника на угол не более 10—15° (можно помочь себе транспортиром). Затем
отпускаем груз и даём маятнику совершить два — три полных колебания, чтобы
процесс колебаний стал установившимся. В момент прохождения маятником крайнего
положения запускаем секундомер. Теперь нам остаётся только дождаться, пока
маятник не совершит 30 полных колебаний. По окончании последнего колебаний
останавливаем секундомер. Значение промежутка времени, за которое маятник
совершил 30 колебаний, записываем в таблицу с учётом погрешности измерения:
Теперь подвесим к маятнику второй груз и повторим
эксперимент. По окончании тридцатого колебания останавливаем секундомер и
записываем значение промежутка времени в таблицу.
Наконец, увеличиваем массу маятника до 300 г и, включив секундомер,
вновь отсчитываем 30 полных колебаний. Не забываем записать в таблицу значение
промежутка времени с учётом погрешности измерения:
Прямые измерения мы с вами завершили. Теперь определяем
период колебаний. Для этого подставляем в расчётную формулу значения
промежутков времени и числа полных колебаний для каждого из трёх случаев:
Таким образом видим, что в пределах погрешности измерений
период колебаний маятника остаётся неизменным. Поэтому в выводе мы
напишем: период колебаний нитяного маятника не зависит от массы груза.
Что касается исследования зависимости частоты колебаний
маятника от его длины, то вся работа остаётся примерно такой же,
что и в нашей первой работе, где мы определяли период колебаний. Отличие будет
состоять только в расчётной формуле. Ведь частота определяет число колебаний,
совершаемых телом за единицу времени:
То же самое
касается и исследования зависимости
частоты колебаний нитяного маятника от массы груза. Ведь в любом
случае, частота — это величина, обратная периоду колебаний.
Формула периода колебаний математического маятника
Формула периода колебаний математического маятника
Математический маятник
Определение
Математический маятник — это частный случай физического маятника, масса которого находится в одной точке.
Обычно математическим маятником считают маленький шарик (материальную точку), имеющий большую массу, подвешенный на длинной нерастяжимой нити (подвесе). Это идеализированная система, которая совершает колебания под воздействием силы тяжести. Только для углов порядка 50-100 математический маятник является гармоническим осциллятором, то есть совершает гармонические колебания.
Изучая качание паникадила на длинной цепи Галилей изучал свойства математического маятника. Он понял, что период колебаний данной системы не зависит от амплитуды при малых углах отклонения.
Формула для периода колебаний математического маятника
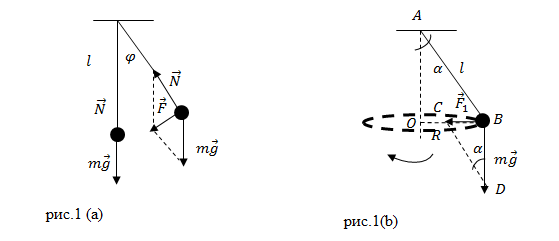
Пусть точка подвеса маятника неподвижна. Груз, подвешенный к нити маятника, движется по дуге окружности (рис.1(a)) с ускорением, на него действует некоторая возвращающая сила ($overline{F}$). Данная сила изменяется при движении груза. В результате чего расчет движения становится сложным. Введем некоторые упрощения. Пусть маятник совершает колебания не в плоскости, а описывает конус (рис.1 (b)). Груз в этом случае перемещается по окружности. Период интересующих нас колебаний будет совпадать с периодом конического движения груза. Период обращения конического маятника по окружности равен времени, которое тратит груз на один виток по окружности:
[T=frac{L}{v}=frac{2pi R}{v}left(1right),]
где $L$ — длина окружности; $v$ — скорость движения груза. Если углы отклонения нити от вертикали малые (небольшие амплитуды колебаний) то полагают, что возвращающая сила ($F_1$) направлена по радиусу окружности, которую описывает груз. Тогда эта сила равна центростремительной силе:
[F_1=frac{mv^2}{R}left(2right).]
Рассмотрим подобные треугольники: AOB и DBC (рис.1 (b)).
[F_1=mg{sin alpha =mgfrac{R}{l} }left(3right).]
Приравниваем правые части выражений (2) и (3), выражаем скорость движения груза:
[frac{mv^2}{R}=mgfrac{R}{l} to v=Rsqrt{frac{g}{l}}left(4right).]
Полученную скорость подставим в формулу (1), имеем:
[T=frac{2pi R}{Rsqrt{frac{g}{l}}}to ]
[T=2pi sqrt{frac{l}{g}}left(5right).]
Из формулы (5) мы видим, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения. Формулу (5) для периода математического маятника называют формулой Гюйгенса, она выполняется, когда точка подвеса маятника не движется.
Используя зависимость периода колебаний математического маятника от ускорения свободного падения, определяют величину данного ускорения. Для этого измеряют длину маятника, рассматривая большое количество колебаний, находят период $T$, затем вычисляют ускорение свободного падения.
Примеры задач с решением
Пример 1
Задание. Как известно, величина ускорения свободного падения зависит от широты. Каково ускорение свободного падения на широте Москвы, если период колебаний математического маятник длиной $l=2,485cdot {10}^{-1}$м равен T=1 c?textit{}
Решение. За основу решения задачи примем формулу периода математического маятника:
[T=2pi sqrt{frac{l}{g}}left(1.1right).]
Выразим из (1.1) ускорение свободного падения:
[g=lfrac{4{pi }^2}{T^2}.]
Вычислим искомое ускорение:
[g=0,2485cdot frac{4{pi }^2}{1^2}=9,81 (frac{м}{с^2}).]
Ответ. $g=9,81frac{м}{с^2}$
Пример 2
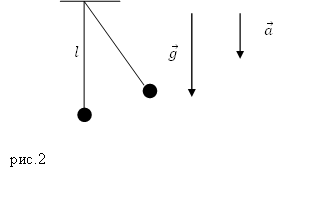
Задание. Каким будет период колебаний математического маятника, если точка его подвеса движется вертикально вниз 1) с постоянной скоростью? 2) с ускорением $a$? Длина нити этого маятника равна $l.$
Решение. Сделаем рисунок.
1) Период математического маятника, точка подвеса которого движется равномерно, равен периоду маятника с неподвижной точкой подвеса:
[T_1=2pi sqrt{frac{l}{g}}left(2.1right).]
2) Ускорение точки подвеса маятника можно рассматривать как появление дополнительной силы, равной $F=ma$, которая направлена против ускорения. То есть, если ускорение направлено вверх, то дополнительная сила направлена вниз, значит, она складывается с силой тяжести ($mg$). Если точка подвеса движется с ускорением, направленным вниз, то дополнительная сила вычитается из силы тяжести.
Период математического маятника, который совершает колебания и у которого точка подвеса движется с ускорением, найдем как:
[T_2=2pi sqrt{frac{l}{a_p}}left(2.2right),]
где:
[a_p=g-a left(2.3right),]
тогда:
[T_1=2pi sqrt{frac{l}{g-a}}.]
Ответ. 1) $T_1=2pi sqrt{frac{l}{g}}$; 2) $T_1=2pi sqrt{frac{l}{g-a}}$
Читать дальше: формула периода колебаний пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Математический маятник — идеальная конструкция, представляющая собой тело с точечной массой, подвешенное на упругой нити. При описании колебаний такого маятника пренебрегают силами трения, сопротивлением воздуха и прочими потерями энергии, возникающими при работе таких конструкций в реальности.
Период колебаний математического маятника прямо пропорционален длине нити и, при малых углах отклонения, не зависит ни от веса подвешенного груза, ни от амплитуды.
Колебания математического маятника осуществляются под действием двух сил:
- силы тяжести;
- силы упругости нити.
При нулевом отклонении нити от вертикали сила упругости уравновешивает силу тяжести. При отклонении между ними возникает тупой угол, зная который и сложив векторы сил тяжести и упругости можно найти результирующую силу. Она действует по касательной (тангенциально) к дуге, по которой перемещается груз маятника:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
$F_{tang} = m cdot sin(alpha)$,
где $alpha$ — угол отклонения нити от вертикали.
Тангенциальная сила изменяется в течение цикла от нуля в моменты наибольших отклонений до максимума в нижней точке. Чтобы упростить задачу, можно мысленно заставить маятник описывать конус вокруг вертикальной оси с периодом обращения равным периоду колебаний. Тогда время одного витка будет составлять
$T = frac{L}{v} = frac{2pi cdot R}{v}$,
где $L$ — длина кругового пути, $R$ — радиус окружности, по которой движется груз, $v$ — скорость груза. Сила, стремящаяся вернуть маятник в состояние покоя (к центру системы) и действующая перпендикулярно оси вращения, вычисляется по формуле:
$F_c = frac{m cdot v^2}{R}$
Ее можно выразить и геометрически, как зависящую от силы тяжести:
$F_c = m cdot g cdot sin(alpha) = m cdot g cdot frac{R}{l}$,
где $l$ — длина нити.
Сопоставив оба варианта выражения центростремительной силы, найдем зависимость периода колебаний маятника от длины нити:
$frac{m cdot v^2}{R} = m cdot g cdot frac{R}{l} implies v = R cdot sqrt{g}{l} implies T = 2pi cdot sqrt{frac{l}{g}}$
Пример 1
Каково ускорение свободного падения в географической точке, где период колебаний математического маятника длиной $0,249$ м равен 1 c?
Выразим ускорение свободного падения из формулы:
$g = l cdot frac{4pi^2}{T^2}$
Подставим числовые значения:
$g = 0,249 cdot frac{4 cdot 3,1415927^2}{1^2} approx 9,83$
Ответ: $approx 9,83 frac{Н}{с^2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Период математического маятника — период колебания математического маятника зависит от длины нити: с уменьшением длины нити период колебания уменьшается
Для математического маятника выполняются некоторые законы:
1 закон. Если, сохраняя одну и ту же длину маятника, подвешивать разные грузы (например 5кг и 100 кг), то период колебаний получится один и тот же, хотя массы грузов сильно различаются. Период математического маятника не зависит от массы груза.
2 закон. Если маятник отклонять на разные, но маленькие углы, то он будет колебаться с одним и тем же периодом, хотя и с разными амплитудами. Пока амплитуда маятника будут малы, колебания и по своей форме будут похожи на гармонические, и тогда период математического маятника не зависит от амплитуды колебаний. Это свойство приняло название изохронизмом..
Давайте выведем формулу периода математического маятника.
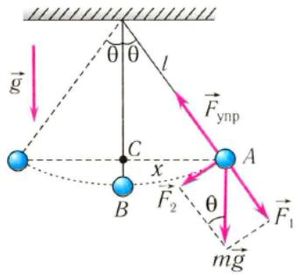
На груз m математического маятника действуют сила тяжести mg и сила упругости нити Fynp. Ось 0Х направим вдоль касательной к траектории движения вверх. Запишем второй закон Ньютона для данного случая:
С проецируем все на ось ОХ:
При малых углах
Сделав замены и маленькие преобразования у нас получается, что уравнение имеет вид:
Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:
Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:
Тогда период математического маятника будет равен:
Период математического маятника зависит только от ускорения свободного падения g и от длины маятника l. Из полученной формулы следует, что период маятника не зависит от его массы и от амплитуды (при условии, что она достаточно мала). Так же мы установили количественную зависимость между периодом маятника, его длиной и ускорением свободного падения. Период математического маятника пропорционален корню квадратному из отношения длины маятника к ускорению свободного падения. Коэффициент пропорциональности равен 2p
Так же есть:
Период пружинного маятника
Период физического маятника
Период крутильного маятника
В Формуле мы использовали :
— Период математического маятника
— Длина подвеса
— Ускорение свободного падения
— Циклическая частота пружинного маятника
— Сила упругости
— Длина дуги АВ