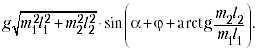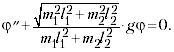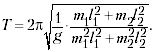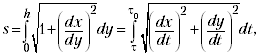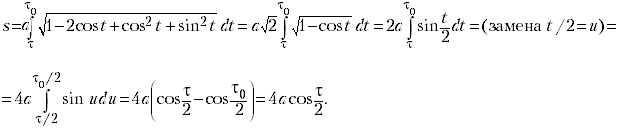Как найти период колебаний формула томсона

На прошлом уроке мы с вами познакомились с электромагнитными
колебаниями. Напомним, что так называют периодические изменения со временем
электрических и магнитных величин в электрической цепи.

Рассмотрев качественную сторону теории процессов в
колебательном контуре, перейдём к её количественной стороне. Для этого рассмотрим
идеальный колебательный контур, то есть контур, активное сопротивление
которого пренебрежимо мало.

В таком контуре, как мы показали ранее, полная
электромагнитная энергия в любой момент времени равна сумме энергий
электрического и магнитного полей, и она не меняется с течением времени:

А раз энергия контура неизменная, то производная полной
энергии по времени равна нулю:

Напомним, что в записанной формуле заряд и сила тока в цепи
являются функцией времени.

Чтобы понять физический смысл этого уравнения, перепишем его
так:

Из такой записи видно, что скорость изменения магнитного
поля по модулю равна скорости изменения энергии электрического поля. А знак
минус в формуле показывает на то, что увеличение энергии магнитного поля
происходит за счёт убыли энергии поля электрического.

Вычислим производные в записанном уравнении, воспользовавшись
для этого формулой вычисления производной сложной функции.

А теперь вспомним, что производная заряда по времени есть
сила мгновенного тока (то есть сила тока в данный момент времени):

Поэтому предыдущее уравнение можно переписать так, как показано
на экране:

Производная силы тока по времени есть не что иное, как вторая
производная заряда по времени, подобно тому, как производная скорости по
времени (то есть ускорение) есть вторая производная координаты по времени:

Перепишем предыдущее равенство с учётом этой поправки:

Разделив левую и правую части этого уравнения на «Эль И» (Li),
получим основное уравнение, описывающее свободные гармонические
электрические колебания в контуре:

Данное уравнение аналогично уравнению, описывающему
гармонические механические колебания:

Отсюда видно, что величина, обратная квадратному корню из
произведения индуктивности и ёмкости, является циклической частотой свободных
электрических колебаний:

Зная циклическую частоту колебаний, нетрудно найти и их
период, то есть минимальный промежуток времени, через который процесс в
колебательном контуре полностью повторяется:

Эта формула впервые была получена английским физиком Уильямом
Томсоном 1853 году, и в настоящее время носит его имя.

Из формулы видно, что период колебательного контура
определяется параметрами составляющих его элементов: индуктивностью катушки и
ёмкостью конденсатора. Из формулы Томсона также следует, что, например, при
уменьшении ёмкости или индуктивности период колебаний должен уменьшиться, а их
частота — увеличиться и наоборот.

Но вернёмся к уравнению свободных электромагнитных колебаний
в идеальном колебательном контуре. Его решением является уравнение, выражающее
зависимость заряда конденсатора от времени:

В записанной формуле q_m — это начальное
(или амплитудное) значение заряда, сообщённому конденсатору. Из этой формулы
следует, что заряд на конденсаторе изменяется со временем по гармоническому
закону.

Если взять первую производную заряда конденсатора по времени,
то мы получим уравнение, описывающее изменение силы тока в контуре:

Величина, равная произведению максимального заряда
конденсатора и циклической частоты колебаний, является амплитудным значением
силы тока:

Перепишем уравнение для силы тока с учётом последнего
равенства, а также воспользовавшись формулой приведения:

Из такой записи хорошо видно, что сила тока в колебательном
контуре также совершает гармонические колебания с той же частотой, но по фазе
она смещена на π/2 относительно колебаний заряда.

Для закрепления материала, решим с вами такую задачу. Конденсатор
ёмкостью 2 мкФ зарядили до напряжения 100 В, а затем замкнули на катушку с
индуктивностью 5 мГн. Определите заряд конденсатора через 0,025π мс после
замыкания.

В заключение отметим, что в реальных колебательных контурах всегда
имеется активное сопротивление, поэтому часть энергии контура всегда превращается
во внутреннюю проводников, которая выделяется в виде излучения. Кроме того,
часть энергии теряется на перемагничивание сердечника и изменение поляризации
диэлектрика. Поэтому полная энергия контура с течением времени уменьшается, в
результате уменьшается и амплитуда колебаний. Следовательно, реальные
электромагнитные колебания в контуре являются затухающими.

Колебательный контур

• Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

• Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур.

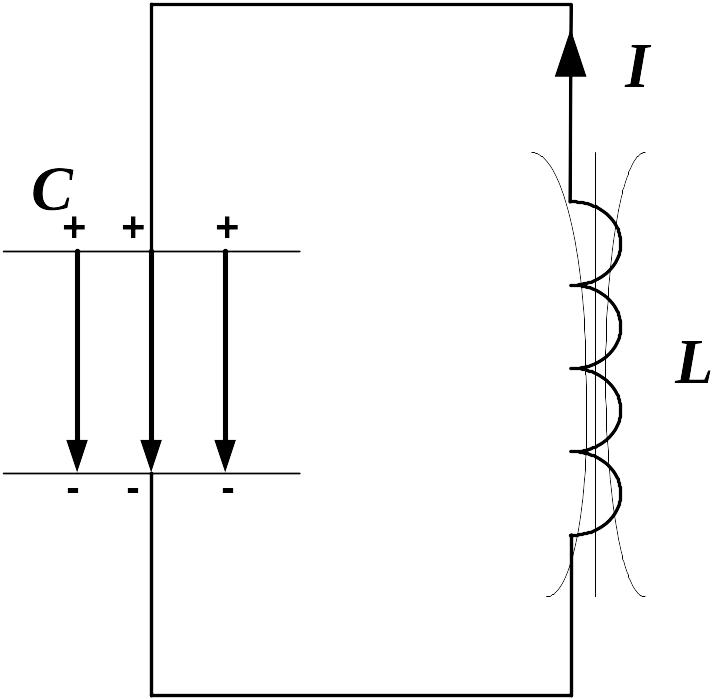
• Идеальный колебательный контур (LC-контур) — электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

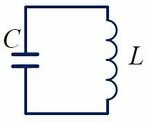
На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

(W=W_{e} + W_{m}, ; ; ; W_{e} =dfrac{Ccdot u^{2} }{2} = dfrac{q^{2} }{2C}, ; ; ; W_{m} =dfrac{Lcdot i^{2}}{2},)

где W_e — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, W_m — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.

Процессы в колебательном контуре

Рассмотрим процессы, которые возникают в колебательном контуре.

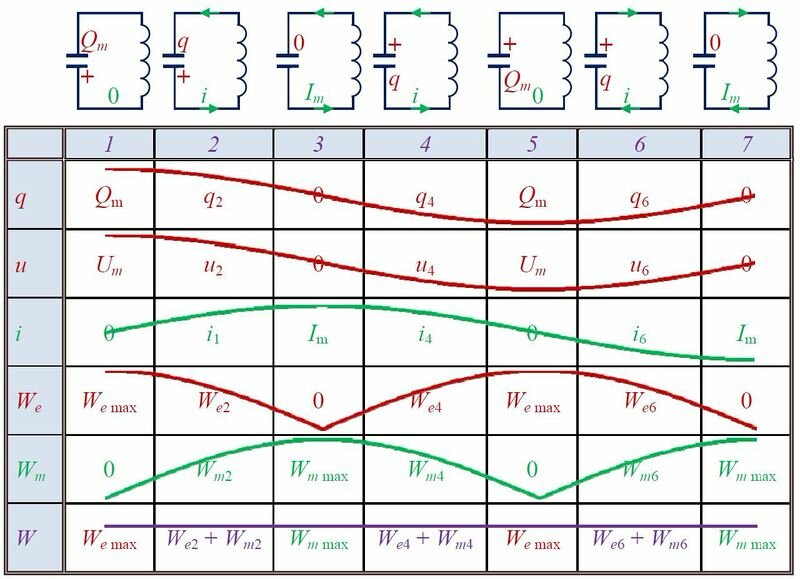
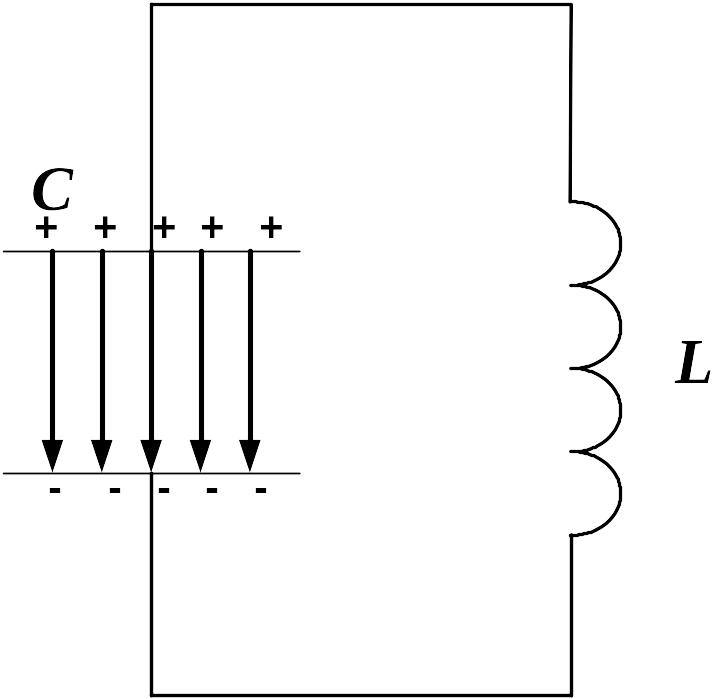
Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m (рис. 2, положение 1). С учетом уравнения (U_{m}=dfrac{Q_{m}}{C}) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2). Вместе с зарядом q будет уменьшаться и напряжение u (left(u = dfrac{q}{C} right).) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I_m (см. рис. 2, положение 3).

Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I_m (в положении 3) оказывается максимальным значением силы тока в контуре.

Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m) (см. рис. 2, положение 5).

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6)до нуля (см. рис. 2, положение 7). И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e (left(W_{e}=dfrac{q^{2}}{2C}=dfrac{C cdot u^{2}}{2} right),) а сила тока в катушке i — энергию магнитного поля Wm (left(W_{m}=dfrac{L cdot i^{2}}{2} right),) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Обозначения в таблице:

Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку в нем потерь энергии (нет сопротивления). Тогда

(W=W_{e, max } = W_{m, max } = W_{e2} + W_{m2} = W_{e4} +W_{m4} = …)

Свободные электромагнитные колебания

Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока i, заряда q и напряжения u, причем полная энергия контура при этом будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

• Свободные электромагнитные колебания в контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q и сила тока в катушке i достигают своих максимальных значений Q_m и I_m в различные моменты времени.

Свободные электромагнитные колебания в контуре происходят по гармоническому закону:

(q=Q_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; u=U_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; i=I_{m} cdot cos left(omega cdot t+varphi _{2} right).)

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в LC-контуре определяется по формуле Томсона:

(T=2pi cdot sqrt{Lcdot C}, ;;; omega =dfrac{1}{sqrt{Lcdot C}}.)

Сточки зрения механической аналогии, идеальному колебательному контурусоответствует пружинный маятник без трения, а реальному — с трением. Вследствиедействия сил трения колебания пружинного маятника затухают с течением времени.

*Вывод формулы Томсона

Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

(W=dfrac{Q_{m}^{2} }{2C} =dfrac{Lcdot I_{m}^{2} }{2} =dfrac{q^{2} }{2C} +dfrac{Lcdot i^{2} }{2} ={rm const}.)

Получим уравнение колебаний в LC-контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что

(W’=0, ;;; q’=i, ;;; i’=q»,)

получаем уравнение, описывающее свободные колебания в идеальном контуре:

Переписав его в виде:

(q»+omega ^{2} cdot q=0,)

замечаем, что это — уравнение гармонических колебаний с циклической частотой

(omega =dfrac{1}{sqrt{Lcdot C} }.)

Соответственно период рассматриваемых колебаний

(T=dfrac{2pi }{omega } =2pi cdot sqrt{Lcdot C}.)

Литература

1. Жилко, В.В. Физика: учеб. пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, Л.Г. Маркович. — Минск: Нар. Асвета, 2009. — С. 39-43.

Колебательный контур. Формула Томсона

Основным устройством,
определяющим рабочую частоту любого
генератора переменного тока, является
колебательный контур. Колебательный
контур (рис.1) состоит из катушки
индуктивности L
(рассмотрим идеальный случай, когда
катушка не обладает омическим
сопротивлением) и конденсатора C
и называется замкнутым. Характеристикой
катушки является индуктивность, она
обозначается L
и измеряется в Генри (Гн), конденсатор
характеризуют емкостью C,
которую измеряют в фарадах (Ф).

Пусть в начальный
момент времени конденсатор заряжен
так (рис.1), что на одной из его обкладок
имеется заряд +Q₀,
а на другой – заряд —Q₀.
При этом между пластинами конденсатора
образуется электрическое поле, обладающее
энергией

,
(1)

где


– амплитудное
(максимальное) напряжение или разность
потенциалов на обкладках конденсатора.

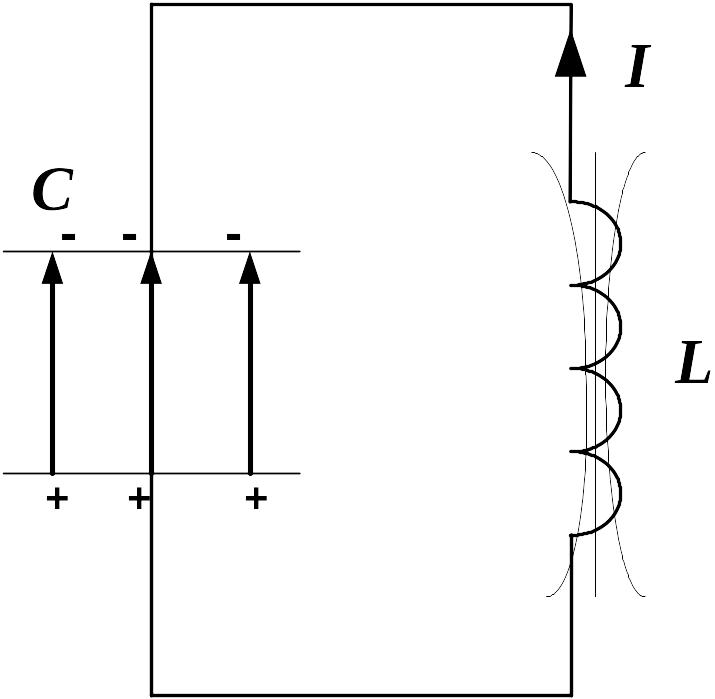
После замыкания
контура конденсатор начинает разряжаться
и по цепи пойдет электрический ток
(рис.2), величина которого увеличивается
от нуля до максимального значения

.
Так как в цепи протекает переменный по
величине ток, то в катушке индуцируется
ЭДС самоиндукции, которая препятствует
разрядке конденсатора. Поэтому процесс
разрядки конденсатора происходит не
мгновенно, а постепенно. В каждый момент
времени разность потенциалов на
обкладках конденсатора

(2)

(где

– заряд конденсатора в данный момент
времени) равна разности потенциалов
на катушке, т.е. равна ЭДС самоиндукции

.
(3)

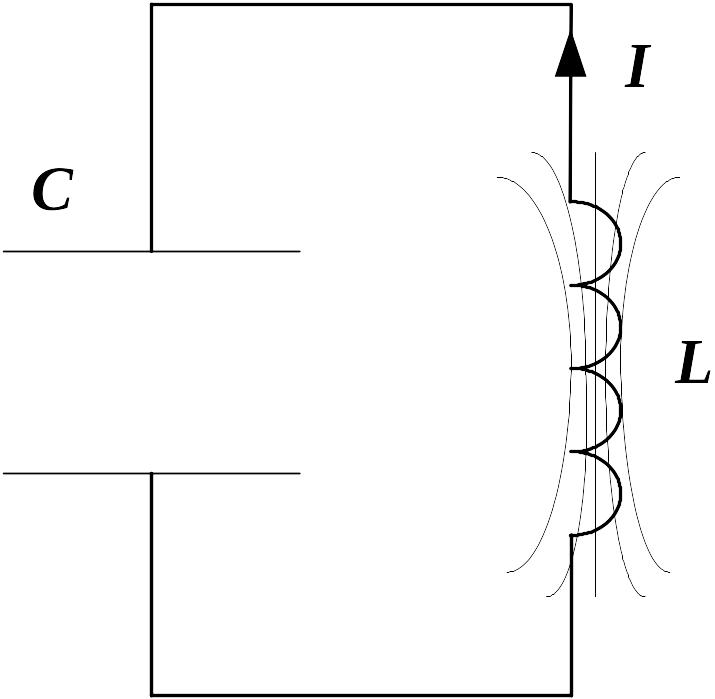
Когда конденсатор
полностью разрядится

и

,
сила тока в катушке достигнет максимального
значения

(рис.3). Индукция магнитного поля катушки
в этот момент также максимальна, а
энергия магнитного поля будет равна

.
(4)

Затем сила тока
начинает уменьшаться, а заряд будет
накапливаться на пластинах конденсатора
(рис.4). Когда сила тока уменьшится до
нуля, заряд конденсатора достигнет
максимального значения
Q₀,
но обкладка, прежде заряженная
положительно, теперь будет заряжена
отрицательно (рис.5). Затем конденсатор
вновь начинает разряжаться, причем ток
в цепи потечет в противоположном
направлении. Так процесс перетекания
заряда с одной обкладки конденсатора
на другую через катушку индуктивности
повторяется снова и снова. Говорят, что
в контуре происходят электромагнитные
колебания.
Этот процесс связан не только с
колебаниями величины заряда и напряжения
на конденсаторе, силы тока в катушке,
но и перекачкой энергии из электрического
поля в магнитное и обратно.

Перезарядка
конденсатора до максимального напряжения

произойдет только в том случае, когда
в колебательном контуре нет потерь
энергии. Такой контур называется
идеальным. В реальных контурах имеют
место следующие потери энергии: 1)
тепловые потери, т.к. R

0; 2) потери в диэлектрике конденсатора;
3) гистерезисные потери в сердечнике
катушке; 4) потери на излучение и др.
Если пренебречь этими потерями энергии,
то можно написать, что

,
т.е.

.
(5)

Колебания,
происходящие в идеальном колебательном
контуре, в котором выполняется это
условие, называются свободными,
или собственными,
колебаниями контура.

В этом случае
напряжение U
(и заряд Q)
на конденсаторе изменяется по
гармоническому закону:

,
(6)

где 
— собственная частота колебательного
контура, ₀
= 2
— собственная (круговая) частота
колебательного контура. Частота
электромагнитных колебаний в контуре
определяется как

или

.
(7)

Период
T
– время, в течение которого совершается
одно полное колебание напряжения на
конденсаторе и тока в контуре, определяется
формулой Томсона

.
(8)

Сила тока в контуре
также изменяется по гармоническому
закону, но отстает от напряжения по
фазе на

.
Поэтому зависимость силы тока в цепи
от времени будет иметь вид

.
(9)

На рис.6 представлены
графики изменения напряжения U
на конденсаторе и тока I
в катушке для идеального колебательного
контура.

В реальном контуре
энергия с каждым колебанием будет
убывать. Амплитуды напряжения на
конденсаторе и тока в контуре будут
убывать, такие колебания называются
затухающими. В задающих генераторах
их применять нельзя, т.к. прибор будет
работать в лучшем случае в импульсном
режиме.

Для получения
незатухающих колебаний необходимо
компенсировать потери энергии при
самых разнообразных рабочих частотах
приборов, в том числе и применяемых в
медицине.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Период гармонических колебаний

В.Б.ДРОЗДОВ, г. Рязань

Период гармонических колебаний

В учебнике «Физика-11» (Г.Я.Мякишев,
Б.Б.Буховцев. – М.: Просвещение, 2004) дан вывод
формулы Томсона
основанный на постоянстве полной
электромагнитной энергии колебательного
контура. Представляет интерес применить этот
метод к различным колебательным системам, в
которых происходят свободные незатухающие
гармонические колебания, для определения
периода этих колебаний. Данный способ позволяет
получить дифференциальное уравнение колебаний откуда следует
формула для периода колебаний При этом достигается
единообразие в решении различных задач на
определение периода колебаний, а также
достигается элементарное решение ряда задач.
Становится возможным, не выходя за рамки
школьного курса, определить период колебаний
некоторых физических маятников. Такого рода
задачи предлагаются на вступительных экзаменах
в вузы с повышенными требованиями по физике.
Рассмотрим конкретные примеры.

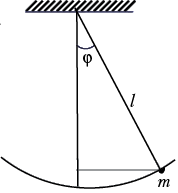
1. Математический маятник.

Пусть
– мгновенное значение скорости маятника,
соответствующее отклонению нити от вертикали на
угол . Тогда
кинетическая энергия маятника потенциальная энергия

E_p = mgl(1 – cos ).

По закону сохранения энергии,

Дифференцируем равенство по времени t,
учитывая что
Так как ‘ = 0
лишь в моменты максимального отклонения
маятника от положения равновесия, то – дифференциальное
уравнение движения математического маятника.
Пусть 1, значит, sin . Тогда из уравнения
гармонических колебаний получим период

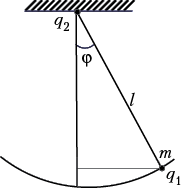
Рассмотрим маятник, несущий
электрический заряд q₁, если в точку
подвеса помещён заряд q₂. Имеем:

Слагаемое

не зависит от времени, следовательно,
получится такое же уравнение колебаний, что и для
незаряженного маятника. Поэтому период
колебаний от зарядов q₁ и q₂
не зависит.

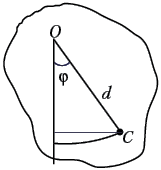
2. Физический маятник.
Физический маятник – это твёрдое тело, которое
может качаться вокруг неподвижной
горизонтальной оси. Масса маятника m, момент
инерции относительно оси J. Расстояние между
центром масс маятника C и точкой подвеса O
равно d.

Пусть – мгновенное значение угловой
скорости маятника, соответствующее отклонению
отрезка OC от вертикали на угол . По закону сохранения
энергии,

Дифференцируем это равенство по
времени t, учитывая, что = ‘. В результате имеем
дифференциальное уравнение колебаний:

а для
малых углов –
уравнение гармонических колебаний с периодом

3. Задача Ф 477 («Квант», 1977, № 9).

Резиновое кольцо массой M лежит на
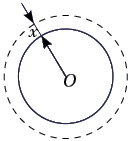
гладкой горизонтальной плоскости. Кольцо
немного растягивают так, что оно сохраняет форму
окружности и центр его остаётся неподвижным.
После этого кольцо отпускают. Опишите дальнейшее
поведение кольца. Коэффициент упругости
резинового жгута равен k.

Решение. Пусть на рисунке x –
мгновенное смещение элементов кольца от
положения равновесия, соответствующее скорости этих элементов. Так
как все элементы кольца движутся с одной и той же
скоростью, то его кинетическая энергия E_k
= M²/2.

Поскольку кольцо растянуто на 2x, то его потенциальная
энергия По закону  сохранения энергии,

Дифференцируем это равенство по
времени, принимая во внимание, что = x’. Получим: – уравнение гармонических
колебаний с периодом

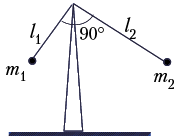
4. Задача Ф 380 («Квант», 1976, № 2).

Найдите период малых колебаний
системы из двух жёстко скреплённых под прямым
углом стержней с шарами на концах. Стержни
считать невесомыми, их длины l₁ и l₂,
массы шаров m₁ и m₂.

Решение. Определим угол , который образует стержень l₂
с вертикалью в положении равновесия, исходя из
того, что в состоянии равновесия потенциальная
энергия системы минимальна: откуда m₁gl_lsin + m₂gl₂cos = max.

Применяя формулу

получим: минимум потенциальной
энергии системы будет при

         (1)

Кинетическая энергия колебательной
системы

где –
угловая скорость вращения стержней l₁
и l₂ вокруг точки O. Пусть 1
рад – угол, на который отклонились стержни от
положения равновесия, тогда потенциальная
энергия системы

E_p = m₁gh – m₁gl₁
+ m₂gh
– m₂gl₂cos( + ) =
(m₁ + m₂)gh – g[m₁l₁sin( + ) + m₂l₂cos( + )] =

= (m₁ + m₂)gh –

С учётом равенства (1) имеем:

E_p = (m₁ + m₂)
gh –

Закон сохранения энергии даёт
уравнение

откуда при 1 получим
уравнение гармонических колебаний:

Период колебаний

Энергетический метод позволяет
упростить элементарное решение задачи (без
использования формулы для периода колебаний
физического маятника). Наиболее же простое
решение получится, если применить формулу

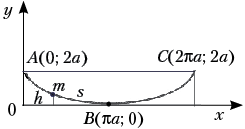
5. Циклоидальный маятник.

Рассмотрим материальную точку,
скользящую без трения по траектории, имеющей
форму одной арки циклоиды, обращённой
выпуклостью вниз. Параметрические уравнения
циклоиды:

По закону сохранения энергии,

где и h
– соответствующие дуге s скорость точки и её
высота над осью абсцисс. Длину дуги s
отсчитываем от положения равновесия точки на
циклоиде.

Скорость точки  = s’.
Из системы уравнений нетрудно получить h = s²/(8a).
Тогда Из
последнего уравнения имеем: – уравнение гармонических
колебаний с периодом

КОММЕНТАРИЙ РЕДАКЦИИ: «Так ли уж
„нетрудно” получить?»

Задав циклоиду в параметрическом виде

x = a(t – sin t),

y = a(1 + cos t).

вычислим длину дуги циклоиды от её
нижней точки до точки, где у = h, лежащей
левее нижней точки (в точности, как у автора).
Сведения из математического анализа дают рецепт:

где ₀
= отвечает нижней
точке циклоиды,
< отвечает точке
циклоиды, в которой y = h;

В таком случае

Как мы договорились выше, y() = a(1+cos) = h. Поэтому

В итоге как и
обещал любезный автор. И никаких особенных
умений не нужно. Какой-то вузовский курс
матанализа плюс некие навыки нехитрого
интегрирования. И вот: не прошло и получаса, как
ответ готов.

Мы в редакции будем весьма
признательны автору, если он пришлёт нам
вычисления, которые действительно покажут, что
ответ в задаче «нетрудно получить».

В.Г.ГРИБОВ, к.ф.-м.н.,
доцент физфака МГУ им. М.В.Ломоносова