Как найти периметр сечения призмы плоскостью - AvtoShod.ru

В правильной четырехугольной призме ABCDA₁B₁C₁D₁ точка K  — середина ребра АВ, точка Р  — середина ребра ВС. Через точки K, P, D₁ проведена плоскость α.

а)  Докажите, что сечение призмы плоскостью α можно разбить на две части, одна из которых равнобедренный треугольник, а другая  — равнобокая трапеция.

б)  Найдите периметр сечения призмы плоскостью α, если известно, что сторона основания призмы равна 8, а боковое ребро равно 6.

Решение.

а)  Пусть плоскость KPD₁ пересекает AA₁ в точке M, а CC₁ в точке N. KP параллельна AC, следовательно, KPD₁ параллельна AC. MN лежит в плоскости и KPD_1, значит, MN параллельна AC. Таким образом, AMNC  — параллелограмм MA  =  NC, AK  =  PC, поэтому, MK  =  NC, MN, AC и KP параллельны между собой, то есть KMNP  — равнобедренная трапеция.

Заметим, что A₁M₁  =  C₁N, A₁D₁  =  D₁C₁, таким образом, треугольник D_1MN равнобедренный,

б)  Найдём соотношение в котором MN делит ребра AA_1 и CC_1. Рассмотрим плоскость R  — точка пересечения плоскости с KP, а Q  — с MN, O  — центр грани ABCD. Имеем:

Значит,

Тогда:

Ответ: б)

Источник

Ответ:

10 ед.

Объяснение:

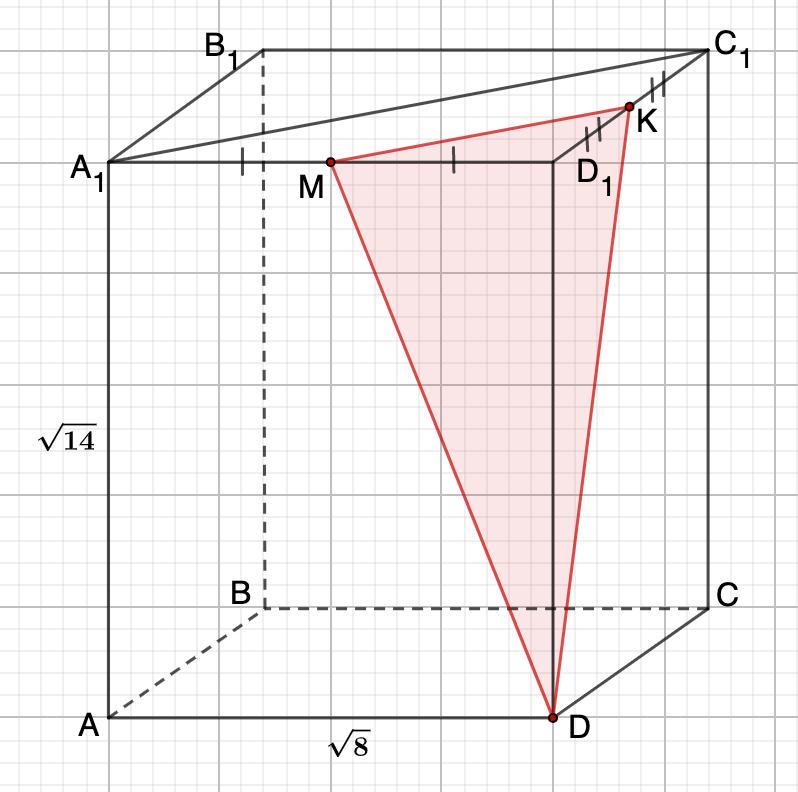
Дано: Правильная призма ABCDA₁B₁C₁D₁;

A₁M=MD₁; D₁K=KC₁;

AA₁=√14; AD=√8

Найти: Рс — периметр сечения.

Решение:

Призма правильная ⇒ в основании квадрат.

1) Рассмотрим ΔA₁C₁D₁ — прямоугольный, равнобедренный.

$A_1C_1=sqrt{A_1D_1^2+D_1C_1^2}=sqrt{8+8}=4$

A₁M=MD₁; D₁K=KC₁ (условие)

⇒ МК — средняя линия

МК=А₁С₁:2=4:2=2 (средняя линия равна половине основания)

2) Рассмотрим ΔMDD₁ — прямоугольный.

$displaystyle MD_1=frac{sqrt{8} }{2}=frac{2sqrt{2} }{2}=sqrt{2}$

По теореме Пифагора:

$displaystyle MD=sqrt{MD_1^2+D_1D^2}=sqrt{2+14}=4$

Аналогично

3) Найдем периметр сечения.

Периметр — сумма длин всех сторон треугольника.

$displaystyle P_{DMK}=2+4+4=10$ (ед)

Приложения:

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,662
гуманитарные
33,654
юридические
17,917
школьный раздел
611,985
разное
16,906

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

vevexa122

Вопрос по геометрии:

каждое ребро треугольной призмы равна а. Найдите периметр сечения призмы плоскостью основания и противоположную вершину верхного основания.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

grorisifo643

Правильное условие:

Каждое ребро треугольной призмы равна а. Найдите периметр сечения призмы плоскостью проходящей через сторону основания и противоположную вершину верхнего основания.

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат — это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

Условие задачи

— правильная призма, сторона равна 16. Через точки и лежащие на рёбрах и B B_1 соответственно, проведена плоскость alpha , параллельная прямой AB. Сечение призмы этой плоскостью — четырёхугольник, одна сторона которого равна 16, а три другие равны между собой.

а) Докажите, что периметр сечения плоскостью alpha больше 40.

б) Найдите расстояние от точки до плоскости alpha , если упомянутый периметр равен 46.

Решение

а) Плоскость

Через точку в плоскости (ABB_1) проведём Тогда плоскость (PQM) искомая по признаку параллельности прямой и плоскости ( следовательно, ).

1 случай. Точка совпадает с точкой В этом случае плоскость (PQM) (т. е. alpha ) совпадает с сечение — прямоугольник и с учётом равенства трёх сторон получаем квадрат со стороной, равной 16, и периметром 64, что больше 40.

2 случай. Точка находится внутри отрезка AC. В этом случае плоскость (PQM) не совпадает с Построим сечение призмы плоскостью (PQM). Пусть плоскость (PQM) пересекает нижнюю грань по прямой MN, тогда ( в противном случае пересекается с в некоторой точке и мы получаем противоречие: через три точки , и проходят две различные плоскости). Соединяя точки и , получаем искомое сечение PQMN.

Так как ABPQ — параллелограмм даже прямоугольник, то

Тогда Кроме того, так как следовательно, он равносторонний и Обозначим длины этих отрезков через Четырёхугольник MNPQ — равнобедренная трапеция, так как

В прямоугольном треугольнике BPN ( перпендикулярно плоскости основания) и по теореме Пифагора откуда следует, что и периметр, равный что и требовалось доказать.

б) Так как периметр трапеции MNPQ равен 46, то по результатам первого пункта $displaystyle MQ=MN=NP=frac{46-16}{3}=10, : : AM=16-10=6.$

Расстояние от точки до плоскости (PQM) можно найти как высоту пирамиды с вершиной в точке и основанием, лежащим на плоскости Рассмотрим пирамиду AMQN и найдём её объём двумя способами: $displaystyle V = frac{1}{3} S_{triangle MQN} cdot h = frac{1}{3}S_{triangle AMN} cdot AQ .$

В треугольнике $angle AMN = 180^{circ} - 60^{circ} = 120 ^{circ} ;$ $displaystyle S_{triangle AMN} = frac{1}{2}AM cdot MN cdot sin angle AMN =frac{1}{2}cdot 6 cdot 10 cdot frac{sqrt{3}}{2}=15sqrt{3};$ $displaystyle AQ=sqrt{QM^2 - AM^2 }=sqrt{10^2 - 6^2}=8;$ $displaystyle V=frac{1}{3}S_{triangle AMN}cdot AQ=frac{1}{3}cdot 15sqrt{3}cdot 8=40sqrt{3}.$

Чтобы найти площадь рассмотрим трапецию QMNP и найдём её высоту, равную длине отрезка

Так как трапеция равнобедренная, то по катету и гипотенузе, поэтому $displaystyle QH=PG=frac{16-10}{2}=3,$ $displaystyle MH = sqrt{10^2 - 3^2 }= sqrt{91} ,$ $displaystyle S_{triangle MNQ} = frac{1}{2}MN cdot MH = frac{1}{2} cdot 10 cdot sqrt{91}= 5sqrt{91}.$ Приравнивая объёмы, получим $displaystyle 40 sqrt{3}=frac{1}{3}cdot h cdot 5sqrt{91},$ откуда $displaystyle h = frac{3 cdot 40 sqrt{3}}{5sqrt{91}}=frac{24 sqrt{3}}{sqrt{91}}.$

Ответ:

б) $displaystyle frac{24sqrt{3}}{sqrt{91}}.$

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Решение. Задание 14, Диагностическая работа 16.12.20» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
13.05.2023

Источник

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Есть сомнения?

Не пропустите также: