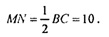Как найти периметр сечения правильного тетраэдра

Лучший ответ

еще ответы

ваш ответ

похожие темы

похожие вопросы 5

Онлайн-урок: Каждое ребро тетраэдра DABC равно 2 см. Постройте сечение тетраэдра плоскостью, проходящей через точки В, С и середину ребра AD. Вычислите периметр сечения.

Дано:

DАВС – тетраэдр

Все ребра 2 см

Найти:

1) Сечение через В и С и середину ребра АD

2) P — ?

Решение:

Согласно условию задачи, выполним чертеж (Рис.1):

Рис.1

1) Так как по условию все ребра равны, то перед нами правильный тетраэдр.

Обозначим точкой Е середину ребра АD. Проведем высоту АК, которая является также медианой в треугольнике АВС.

Соединим точки В, С и Е. Треугольник ЕВС – искомое сечение.

2) Периметр сечения равен:

Р = ВС + ЕВ + СЕ

Где ВС = 2 см по условию задачи

Треугольники АЕС и АЕВ равны между собой по двум сторонам и углу между ними, так как:

АВ = АС по условию

АЕ – общая сторона

∠ЕАС = ∠ЕАВ = 60 º так как по условию АВ = АС = ВС

Тогда, из равенства треугольников следует:

ЕС = ЕВ

Треугольник ЕВС – равнобедренный, где ЕК – высота, медиана и биссектриса.

Угол КАВ = 0,5 · САВ = 0,5 · 60 = 30º

Найдем АК:

Треугольник АЕК является прямоугольным, согласно теореме о трех перпендикулярах, где ∠АЕК = 90º

Тогда, по тереме Пифагора:

Тогда периметр равен:

Светило науки — 11749 ответов — 228603 помощи

Найдите периметр и площадь сечения тетраэдра. Дополнительные задачи 102, Геометрия, 10-11 класс, Атанасян Л.С.

Дочка просит помочь, а я уже и не помню геометрию(

Докажите, что плоскость α, проходящая через середины двух ребер основания тетраэдра и вершину, не принадлежащую основанию, параллельна третьему ребру основания. Найдите периметр и площадь сечения тетраэдра плоскостью а, если длины всех ребер тетраэдра равны 20 см.

Здравствуйте. Могу поделиться)
По теореме I пл. DNM || DC (MN — средняя линия ААВС, поэтому МН || ВС ).
Если все ребра тетраэдра равны, тогда в ΔADC отрезок DM — ме­ диана, а значит и высота и биссектриса. Из ΔADM:

ΔAND — ΔAMD (они — прямоугольные, AD — общая гипотенуза,
AM=AN) из равенства треугольников DM= DN;


Рассмотрим ΔMDN.

Проведем в равнобедренном ΔМDN высоту DK.

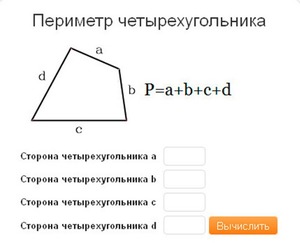
Как найти периметр сторон четырехугольника, формула нахождения

Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.

Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.

Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.

Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме. С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.

Школьное задание

Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?

Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».

Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.

Вопросы:

1. Что такое «периметр»?
2. Как находить периметр четырехугольника?

Ответы на вопросы:

Для тех, кто знает, вспоминаем, а кто не знает — объясняем:

1. Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
2. Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.

Решение:

В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.

2+2+3+3=10

Как мы видим, периметр нашей четырехугольной фигуры равен 10.

В математике сумму всех сторон (периметр) мы обозначаем символом Р.

Теперь записываем правильное решение этой задачи:

Р=2+2+3+3;

Ответ: Р=10.

В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:

P = a + b + c + d (где a , b, c, d являются границами четырехугольника).

Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.

Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.

Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.

На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.

Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.

Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.

В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.

A В D АВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен 60 0. C N S 6. — презентация

Презентация была опубликована 8 лет назад пользователемВсеволод Степухин

Похожие презентации

Презентация на тему: » A В D АВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен 60 0. C N S 6.» — Транскрипт:

2 A В D АВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен C N S 6 см 4 см Повторение

3 Многоугольник ABCDNH – фигура, составленная из отрезков. А ВС D H N А1А1А1А1 А2А2А2А2 А3А3А3А3 А4А4А4А4 А5А5А5А5 А6А6А6А6 А7А7А7А7 Многоугольник A 1 А 2 А 3 А 4 А 5 А 6 А 7 – часть плоскости, ограниченная линией A 1 А 2 А 3 А 4 А 5 А 6 А 7.

4 D А С В … Поверхность, составленная из четырех треугольников … тетраэдром называется тетраэдром Грани Вершины Ребра

5 Тетраэдр. Тетраэдр. Слово составлено из греческих «четыре» и — «основание». Буквальное значение – «четырехгранник». По-видимому, термин впервые употреблен Евклидом. После Платона чаще встречается «пирамида», / С А В SS

6 D А С В Противоположные ребра основание А С В Dоснование

7 Параллелепипед АВСDA 1 B 1 C 1 D 1 – АВСD и A 1 B 1 C 1 D 1 Параллелепипед АВСDA 1 B 1 C 1 D 1 – поверхность, составленная из двух равных параллелограммов АВСD и A 1 B 1 C 1 D 1 и четырех параллелограммов АВВ 1 А 1, ADD 1 A 1, CDD 1 C 1 и ВСС 1 В 1 А В С D D1D1 С1С1 A1A1 B1B1

8 А В С D D1D1 С1С1 A1A1 B1B1 Параллелепипед АВСDA 1 B 1 C 1 D 1 Грани Вершины Ребра Противоположные грани

9 Параллелепипед. Параллелепипед. Слово составлено из греческих «плоскость» «поверхность». Слово встречалось у Эвклида и Герона, но его еще не было у Архимеда.

10 А В С D А1А1 D1D1 С1С1 B1B1 Диагональ параллелепипеда — Диагональ параллелепипеда — отрезок, соединяющий противоположные вершины.

11 Прямоугольный параллелепипед Две грани параллелепипеда называются параллельными, если их плоскости параллельны.

12 А В С D D1D1 С1С1 A1A1 B1B1 Свойства параллелепипеда Противоположные грани параллелепипеда параллельны и равны.

13 А В С D D1D1 С1С1 A1A1 B1B1 Свойства параллелепипеда Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

14 А D С В B1B1 С1С1 D1D1 А1А1 Каково взаимное положение прямых А 1 D и MN, А 1 D и В 1 С 1, МN и A 1 B 1 ? N MRОшибка

15 АD С В B1B1 С1С1 D1D1 А1А1 F E F и E — средины ребер куба. Определите взаимное расположение прямых и угол между прямыми EF и AC.

16 АD С В B1B1 С1С1 D1D1 А1А1 F F — средина ребра DD 1 куба. Определите взаимное расположение прямых BD и B 1 F.R

17 АD С В B1B1 С1С1 D1D1 А1А1 F E F и E — средины ребер куба. Определите взаимное расположение прямых и угол между прямыми В 1 Е и ОF. О

18 АD С В B1B1 С1С1 D1D1 А1А1 F F и Е — средины ребер куба. Определите взаимное расположение прямых АС и FЕ и угол между ними. Е

19 АD С В B1B1 С1С1 D1D1 А1А1 F F и Е — средины ребер куба. Определите взаимное расположение прямых ОЕ и FВ 1. Е О

20 А В С D N M E F F, Е, N, M — средины ребер тетраэдра. Определите взаимное расположение прямых NM и FЕ и угол между ними.

21 А В С D N M N, M — средины ребер тетраэдра. Определите взаимное расположение прямых NM и ВС.

22 А В С D N M N, M, Р и К — средины ребер тетраэдра. Определите взаимное расположение прямых NК и МС. Р К

23 А В С D N N, Р и К — средины ребер тетраэдра. Определите взаимное расположение прямых NВ и РК. Р К

24 А В С D N N и Р — средины ребер тетраэдра. Определите взаимное расположение прямой NР и плоскости АСD Р

25 А В С D Определите взаимное расположение прямой DВ и плоскости АСD

26 А В С D N F, S, N и Р — средины ребер тетраэдра. Определите взаимное расположение прямой CF и плоскости NPS Р S F

27 А В С D N K, F, S, N и Р — средины ребер тетраэдра. Определите взаимное расположение прямой KF и плоскости NPS Р S F K

28 С А В S D В тетраэдре DABC DBC = DBA = ABC = 60 0, BD = BA = BC = 4 см. Найдите площадь грани ADC

29 С А В S D В тетраэдре DABC DBC = DBA = ABC = 90 0, BD = BA = BC = 2 см. Найдите площадь грани ADC

30 А С В D В тетраэдре точка Е – середина ребра ВС. Постройте сечение тетраэдра плоскостью, проходящей через точку Е, параллельно плоскости АDC N Е Р

31 А С В D Е Р N Еще один эскиз к задаче

32 Р E F M S R Пример неудачного эскиза В тетраэдре SMEF все ребра равны 4 см. Найдите периметр сечения, проведенного параллельно ребру MF и проходящего через точки Е и Р, где Р – середина SF.

33 E F M S В тетраэдре SMEF все ребра равны 4 см. Найдите периметр сечения, проведенного параллельно ребру MF и проходящего через точки Е и Р, где Р – середина SF. P Еще один эскиз к задаче R F P S E

34 С А В D В тетраэдре DABC точка М – середина АС, DB=6 см, MD=10см, DBM = Постройте сечение тетраэдра плоскостью, проходящей через середину ребра DC параллельно плоскости DMB, и найдите площадь сечения. M Е R R 6 10

1. Точки M и N лежат в плоскости одной грани ABD. Соединяем их. MN — отрезок сечения.
Точки К и N лежат в плоскости одной грани BDС. Соединяем их. КN — отрезок сечения.
Точки M и К лежат в плоскости одной грани AСD. Соединяем их. MК — отрезок сечения.
MNK — искомое сечение.
Отрезки MN, KN и MK — средние линии соответствующих треугольников, значит MN = KN = MK = а/2.
Pmnk = 3 · a/2 = 3a/2

2. Построение аналогично заданию 1. Попарно соединяем точки M, N и К, так как каждая пара лежит в плоскости одной грани.
Отрезки MN, KN и MK — средние линии соответствующих треугольников, значит MN = KN = MK = а/2.
Pmnk = 3 · a/2 = 3a/2

3. Точки M и N, N и К соединяем, так как каждая пара лежит в плоскости одной грани.
KN║BD как средняя линия треугольника DBC, ⇒ KN║(ABD).
Секущая плоскость проходит через прямую KN и пересекает параллельную ей плоскость (ABD), значит линия пересечения будет параллельна KN.
Проводим ЕМ║BD, а так как KN║BD, то ЕМ║KN.
EMNK — искомое сечение.
ЕМ — средняя линия треугольника ABD, ⇒ ЕМ = а/2,
KN — средняя линия треугольника СBD, ⇒ KN = а/2,
ЕK — средняя линия треугольника ACD, ⇒ ЕK = а/2,
NМ — средняя линия треугольника ABC, ⇒ NМ = а/2,
Pemnk = 4 · a/2 = 2a

4. Точки M и N, N и К соединяем, так как каждая пара лежит в плоскости одной грани.
MN║AC, ⇒ MN║(ADC), секущая плоскость проходит через MN и пересекает (ADC), значит линия пересечения параллельна MN.
Проводим КЕ║АС, а так как MN║AC, ⇒ КЕ║MN.
EMNK — искомое сечение.

5.  Точки M и N, N и К соединяем, так как каждая пара лежит в плоскости одной грани.
(АDC) ∩ (ABC) = АC. Прямые КN и АС лежат в одной плоскости, точка их пересечения — Р.
Точки М и Р лежат в одной плоскости (АВС), прямая МР пересекает ребро АВ в точке Е.
EMNK — искомое сечение.

6. Точки M и N, N и К соединяем, так как каждая пара лежит в плоскости одной грани.
(ВDC) ∩ (ABC) = ВC. Прямые МN и ВС лежат в одной плоскости, точка их пересечения — Р.
Точки К и Р лежат в одной плоскости (АВС), прямая КР пересекает ребро АВ в точке Е.
EMNK — искомое сечение.