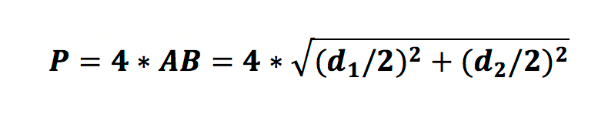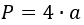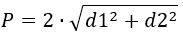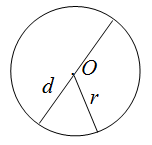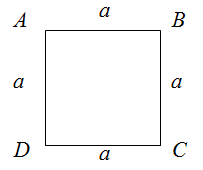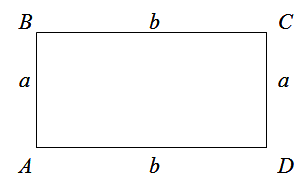Как найти периметр равнобедренного ромба

В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.

  • Формула вычисления периметра

  • Примеры задач

Формула вычисления периметра

1. По длине стороны

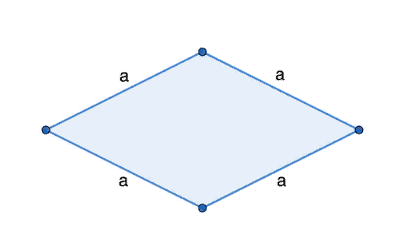
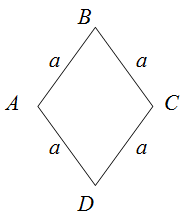
Периметр (P) ромба равняется сумме длин всех его сторон.

P = a + a + a + a

Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):

P = 4*a

Периметр ромба

2. По длине диагоналей

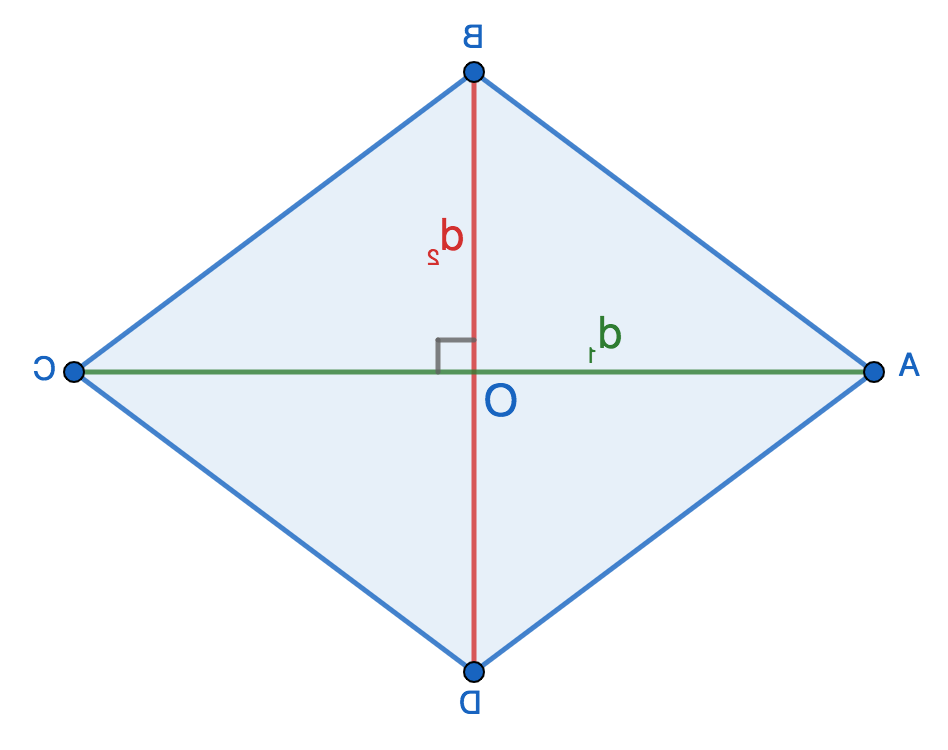
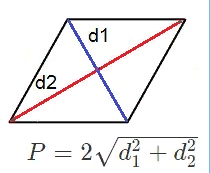
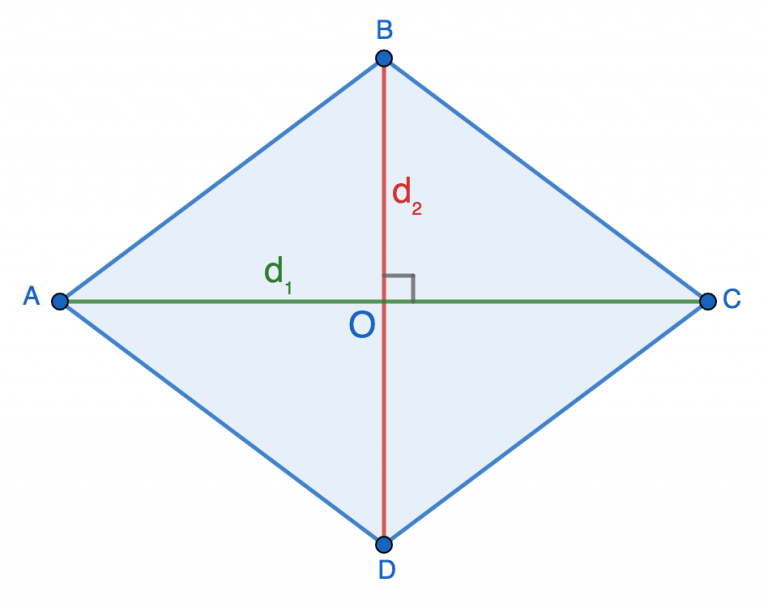
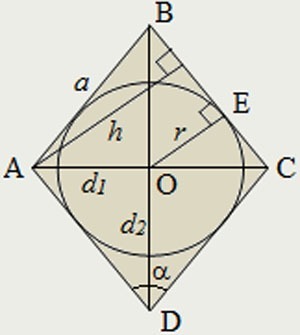
Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:

  • AO=OC=d1/2
  • BO=OD=d2/2

Периметр ромба через диагонали

Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.

Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:

AB2 = AO2 + OB2

Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:

AB2 = (d1/2)2 + (d2/2)2, или

Сторона ромба через диагонали

Таким образом, периметр равняется:

Периметр ромба через диагонали

Примеры задач

Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.

Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.

Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.

Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.

Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.

Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:

Периметр ромба через диагонали

Источник

Что нужно знать о периметре ромба — основные сведения

Содержание:

  • Основные сведения о фигуре ромб

    • Понятие периметра ромба
  • Способы нахождения периметра

    • Через стороны
    • Через длину диагонали
  • Формулы для каждого способа
  • Примеры решения задач

imagetools0.png

Источник: microexcel.ru

Основные сведения о фигуре ромб

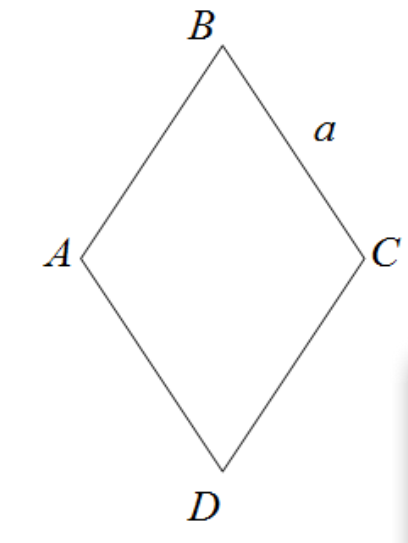
Рассмотрим особый вид параллелограмма, для которого характерны следующие признаки:

  1. Две стороны, являющиеся смежными, равны по величине.
  2. Проведенные из углов диагонали пересекаются в центре фигуры таким образом, что образуют прямой угол.
  3. Определенная диагональ разделяет углы, которые она соединяет, пополам.

По этим признакам можно четко определить, когда параллелограмм является ромбом.

Ромбом называется геометрическая фигура, которая является параллелограммом и имеет все четыре стороны равной длины.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Произошло название от греческого слова ῥόμβος либо латинского rombus. В переводе они означают «бубен».

При этом геометрическими свойствами ромба являются:

  1. Поскольку ромб — параллелограмм, его стороны, лежащие противоположно, имеют равные величины и попарную параллельность. Кроме этого, для всех ромбов характерно равенство противоположных углов, а также факт, что соседние с ними углы составляют в сумме 180о.
  2. С помощью проведения диагоналей можно разделить ромб на четыре треугольника, имеющих прямые углы. При этом диагонали пересекутся в центре фигуры в точке, которая разделит их пополам.
  3. Вышеуказанные диагонали будут биссектрисами углов ромба.
  4. Если длину диагоналей возвести в квадрат и сложить эти квадраты, то получишь квадрат стороны, увеличенный в 4 раза (данное свойство вытекает из тождества параллелограмма).
  5. В ромб можно вписать прямоугольник, при этом его углы будут располагаться на серединах его сторон.
  6. Оси симметрии ромба обязательно будут перпендикулярны диагоналям ромба.
  7. Кроме прямоугольника в ромб можно вписать окружность. Ее центр будет совпадать с точкой, в которой пересекаются диагонали.

Зная вышеизложенные свойства, легко проводить вычисления величин, характеризующих данный ромб и строить внутри него геометрические фигуры.

Понятие периметра ромба

Периметр любой плоской геометрической фигуры составляет сумму длин его границ. Ромб не является исключением.

Исходя из определения, единицы измерения периметра аналогичны единицам длины.

Однако найти периметр ромба можно не только сложив длины всех четырех сторон. В геометрии существует еще один метод, который детально будет рассмотрен ниже.

Способы нахождения периметра

Через стороны

Поскольку у ромба все четыре стороны равны, его периметр можно выразить произведением длины одной стороны на 4.

P=4a

где P — периметр, a — длина стороны.

blobid1648285338122.png

Источник: ru.solverbook.com

Нахождение периметра ромба можно проводить по еще одной формуле, используя длины диагоналей.

Через длину диагонали

Рассмотрим рисунок.

blobid1648285047295.png

Источник: microexcel.ru

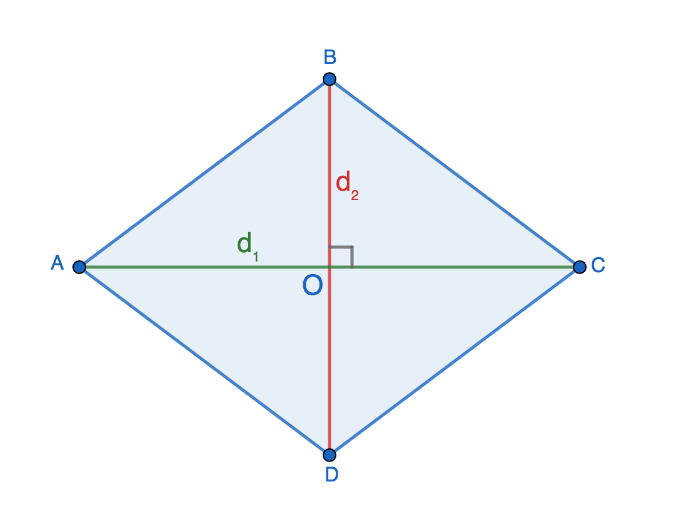
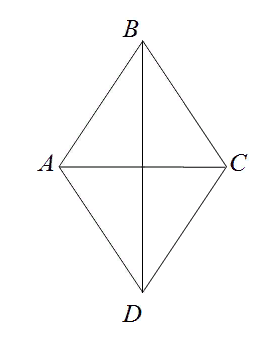
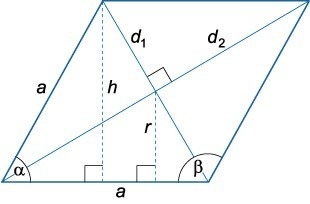
Проведем в ромбе ABCD диагонали BD и AC. Они пересекаются в точке O под прямым углом и делятся этой точкой пополам. Можно записать равенства:

AO=OC=d1/2

BO=OD=d2/2

В результате деления ромба диагоналями на четыре треугольника, имеющих прямые углы, образовались геометрические фигуры AOB, AOD, BOC, DOC. Подробнее рассмотрим один треугольник — AOB.

Из рисунка видно, что сторона AB являясь стороной ромба, представляет собой гипотенузу в прямоугольнике. Далее воспользуемся известной теоремой Пифагора:

AB2=AO2+OB2

В эту формулу подставим величины длин катетов. Однако перед этим выразим их через ½ диагоналей.

AB2=(d1/2)2+(d2/2)2

Извлекая квадрат из этого выражения, получаем:

AB=√((d1/2)2+(d2/2)2)

В итоге находим периметр ромба:

blobid1648286458929.png

 Источник: microexcel.ru

Формулы для каждого способа

В ходе решения задач по теме «ромб» применяются следующие формулы:

  1. Для нахождения периметра:

Через длину стороны: P=4a

blobid1648318436525.png

Источник: microexcel.ru

Используя длины диагоналей:

blobid1648318793756.png

Источник: calculators.vip

Кроме этого, на уроках по изучению характеристик ромба, рассматриваются формулы по нахождению его площади. Ее можно определить с помощью двух способов: через вычисление произведения высоты на длину стороны или половину произведения двух диагоналей.

blobid1648319101517.png

Источник: www.webmath.ru

Примеры решения задач

Задача 1

Длина стороны ромба составляет 10 см. Чему равен его периметр?

Решение.

Находить следует с использованием формулы: P=4a. Подставляем значение длины стороны и получаем P=40 см

Задача 2

Периметр ромба равен 36 см. Чему равна длина его стороны?

Решение.

Используется формула для нахождения периметра. Из нее вытекает действие для нахождения длины стороны: a=P/4

a=36/4=9 см

Задача 3

Дан ромб с длинами диагоналей 8 и 6 см. Чему равен его периметр?

Решение.

Используем способ нахождения периметра через квадрат из суммы квадратов половины диагоналей:

P=4*√((8/2)2+(6/2)2)=20см

Задача 4

Известно, что в ромбе одна из диагоналей равна 6 см, а один из углов равен 60о. Каков периметр этого ромба?

Решение.

Задача 4

Источник: ru.solverbook.com

Предположим, что длина диагонали AC составляет 6 см, а угол ABC составляет 60о

Обозначим длину стороны ромба (а по определению длины всех сторон равны) буквой a.

По основному свойству ромба о равенстве длин его сторон, треугольник ABC равнобедренный. В то же время, поскольку один из его углов равен 60о, он еще и равносторонний.

a=AC=6см

Теперь применяем формулу для нахождения периметра ромба через длину стороны:

PABCD=4*6=24 см

Источник

Периметр ромба калькулятор онлайн умеет вычислять периметр двумя способами:

  1. По стороне ромба.
  2. По диагоналям ромба.

Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.

Периметр ромба- это сумма всех его сторон. 
Так как у ромба все стороны равны, то периметр равен длине любой его стороны, умноженной на четыре.

Как найти периметр ромба?

Найти периметр ромба очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

1) По стороне ромба


где a- любая из равных сторон ромба.

2) По двум диагонялям


где d1,d2 — диагонали ромба.

Скачать все формулы в формате Word

Источник

В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.

1. По длине стороны

Периметр (P) ромба равняется сумме длин всех его сторон.

Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):

2. По длине диагоналей

Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:

Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.

Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:

Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:

Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.

Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.

Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.

Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.

Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.

Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:

Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.

По определению ромб — это параллелограмм, у которого все стороны равны. Таким образом, формула для нахождения периметра ромба $ABCD$ со стороной $a$ имеет вид:

Задание. Найти периметр ромба $ABCD$ со стороной $a=2,5$ дм.

Решение. Для нахождения периметра ромба $ABCD$ воспользуемся формулой:

Ответ. $P_=10$ (дм)

Задание. Найти периметр ромба $ABCD$, если его диагонали равны соответственно $AC=6$ м и $BD=8$ м.

Решение. Сделаем рисунок.

Ответ. $P_=20$ (м)

Работы любой сложности

Квалифицированная помощь от опытных авторов

  • Периметр ромба
  • Способы нахождения
    • По сторонам
    • По двум диагоналям
    • По диагонали и углу
    • По площади и радиусу вписанной окружности
    • По площади и синусу одного из углов
    • Через большую диагональ и половинный угол
  • Периметр ромба
  • Способы нахождения
    • По сторонам
    • По двум диагоналям
    • По диагонали и углу
    • По площади и радиусу вписанной окружности
    • По площади и синусу одного из углов
    • Через большую диагональ и половинный угол

Периметр ромба

Ромб — это четырехугольник с равными сторонами.

Также его называют параллелограммом, у которого все ребра равны. При этом его противоположные углы тоже равны между собой. Если все углы равны 90 градусов, то это квадрат.

Периметр ромба — сумма длин всего его сторон или произведение любой его стороны на 4.

Способы нахождения

Рассмотрим все способы нахождения периметра этой фигуры.

По сторонам

Как найти периметр ромба

Если нам известны величины одного из его ребер, мы без проблем можем найти P по формуле:

где a — это сторона ромба.

По двум диагоналям

Как найти периметр ромба

Если наш ромб — не квадрат, то две его диагонали будут не равны между собой. Также в любом ромбе они пересекаются под углом 90 градусов, а в точке пересечения делятся пополам. Если обе из них нам известны, то можем вычислить периметр фигуры следующим образом:

где (d_1) и (d_2) — это диагонали четырехугольника.

Подобные вычисления получились исходя из свойств диагоналей равностороннего четырехугольника. Вместе со сторонами фигуры они образуют прямоугольный треугольник. По теореме Пифагора:

По диагонали и углу

Как найти периметр ромба

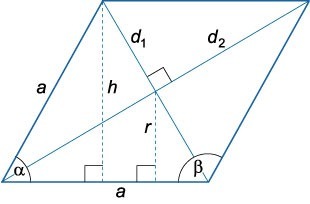
Чтобы вычислить сумму всех ребер ромба данным способом, для начала нужно определить величину одной стороны:

  • если нам известен острый угол α: (a=frac>;)
  • если известен тупой угол (β: a=frac>.)

Далее расчет P будет выглядеть следующим образом:

По площади и радиусу вписанной окружности

Как найти периметр ромба

По известной площади и радиусу вписанной окружности можно находить P, опираясь на формулу:

где r — это радиус вписанной окружности.

По площади и синусу одного из углов

В этом случае формула расчета суммы всех сторон выглядит так:

Через большую диагональ и половинный угол

Как найти периметр ромба

Получите помощь лучших авторов по вашей теме

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Ромб — это параллелограмм, у которого все стороны равны.

Формула периметра ромба ABCD , со сторонами: AB = CD = BC = AD = a

[ LARGE P_ = 4 cdot a ]

где:
P — периметр ромба
a — сторона ромба

Свойства ромба

  • Диагонали ромба перпендикулярны;
  • Диагонали ромба являются биссектрисами его углов.

Признаки ромба

  • Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
  • Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.

Для нахождения периметра заданного ромба воспользуемся формулой

Подставляя значение a = 10 см, получим:

[ P_ = 4 cdot 10 = 40 text <см >]

Периметр ромба равен ( P_ ) = 40 см

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

  • Математика
  • Информатика
  • Финансы
  • Жизнь
  • Здоровье
  • Работа с текстом
  • Работа с цветом
  • Конвертеры
  • Графики
  • Алгебра
  • Геометрия
  • Тригонометрия
  • Физика
  • Химия
  • Литература
  • Информатика
  • Астрономия
  • Законы
  • Единицы измерений
  • Таблицы
  • Инструкции
  • Знаменитые химики
  • Знаменитые физики
  • Знаменитые математики
  • Знаменитые биологи
  • Знаменитые психологи
  • Знаменитые философы
  • ЕГЭ
  • Гаджеты
  • Разное
О сайте

На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.

Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.

calcsbox.com

На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.

  • Пользовательское соглашение
  • Cookie
  • О сайте

© 2021 Все калькуляторы online

Копирование материалов запрещено

Ромб представляет собой параллелограмм, у которого все стороны равны, а углы непрямые. Частным случаем ромба считается квадрат, однако классическая фигура должна иметь два острых и два тупых угла. Ромбические элементы иногда встречаются в реальной жизни, поэтому поиск периметра косоугольника может быть не только школьным заданием, но и житейской задачей.

Геометрия ромба

Ромб — это косоугольник с равными сторонами и равными высотами. Параллелограмм считается ромбом, если соблюдается хотя бы одно из перечисленных условий:

  • диагонали фигуры пересекаются под прямым углом;
  • диагонали одновременно являются биссектрисами углов;
  • смежные стороны фигуры равны, а значит, равны все стороны четырехугольника.

Несколько ромбов с одинаковой длиной стороны могут выглядеть совершенно по-разному. Все дело в различной величине внутренних углов, соответственно, для определения угла фигуры недостаточно знать только длину ее стороны. Для этого необходимо измерить диагонали ромбовидной фигуры, так как они разбивают четырехугольник на 4 прямоугольных треугольника. Кроме того, ромб — симметричная фигура, поэтому его диагонали одновременно являются осями симметрии и биссектрисами для углов, из которых они выходят.

Ромб в реальной жизни

В трехмерной повседневности ромб встречается не слишком часто: наибольшее применение он находит в металлообработке, машиностроении, архитектуре, геральдике и дизайне. К примеру, ромбовидную форму имеют резцы металлообрабатывающих станков, нестандартные ромбические окна или геометрические узоры на коврах или стенных покрытиях. Наиболее очевидным примером ромба в реальности является тротуарная плитка, которая чаще всего выполняется именно в ромбовидной форме. Кроме того, форму ромба имеют отличительные знаки выпускников военных училищ и гражданских учебных заведений. Несмотря на довольно скудное распространение в реальном мире, вам может понадобиться вычислить периметр ромба для решения каких-либо практических задач.

Периметр ромбической фигуры

Периметр вычисляется как сумма длин всех сторон плоской геометрической фигуры. Ромб — четырехугольник с равными между собой сторонами, а значит, его периметр определяется простой формулой:

где a — длина одной стороны.

Если вам необходимо найти периметр ромбовидной фигуры для решения школьных заданий или практических задач, воспользуйтесь нашим онлайн-калькулятором. Для определения периметра наиболее простым способом вам понадобится измерить только сторону ромба, однако алгоритм калькулятора требует ввода двух переменных, поэтому в форму «Высота» введите 1. Также вы можете определить периметр, введя следующие сочетания переменных:

  • две диагонали;
  • диагональ и величина угла.

Примеры из реальной жизни

Рассмотрим пару примеров.

Пример №1

Определите периметр ромба, если длина его стороны равна 6 см. Если дана сторона, то это самый простой способ для определения периметра. Если вы помните простую формулу, то просто умножьте длину на 4. Если же нет, то наш калькулятор к вашим услугам. Введите значение в форму калькулятора, укажите высоту равную 1 и получите простой ответ:

В школьных заданиях определение периметра может усложняться.

Пример №2

Найдите периметр ромбической фигуры, если длина одной его диагонали равна 8 см, а величина острого угла составляет 60 градусов. Решая эту задачу вручную, вам бы понадобилось определять длину стороны, используя тригонометрические расчеты. Однако при помощи нашего сервиса вы можете просто ввести эти данные в форму калькулятора и получить готовый результат в виде:

Вы можете вычислить периметр ромбической фигуры, оперируя разными параметрами. Кроме того, калькулятор автоматически подсчитает все остальные атрибуты ромба, как острый и тупой угол, длины обеих диагоналей и длину стороны.

Заключение

Несмотря на то, что ромбовидные фигуры редко встречаются в реальности, у вас может возникнуть потребность определения периметра ромба, как для решения абстрактных школьных заданий, так и бытовых или производственных вопросов. Используя наш инструментарий, вы быстро и без ошибок вычислите все необходимые атрибуты любой геометрической фигуры.

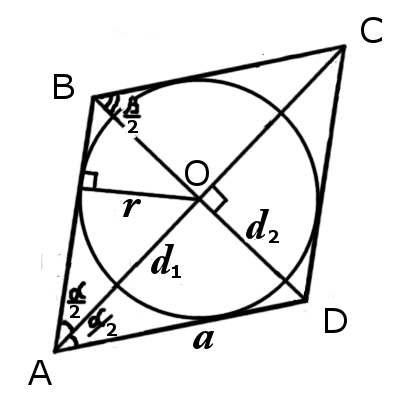Как найти периметр ромба Как найти периметр ромба Рис.1 Рис.2

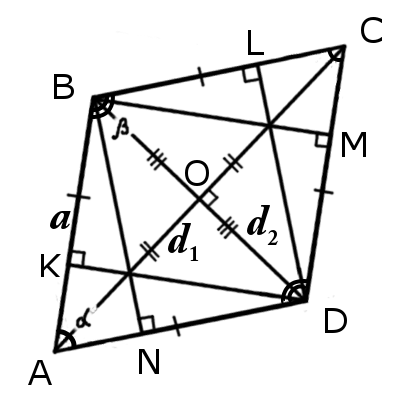
Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

a = S ha
2. Формула стороны ромба через площадь и синус угла:

a = √ S √ sinα

a = √ S √ sinβ
3. Формула стороны ромба через площадь и радиус вписанной окружности:

a = S 2 r
4. Формула стороны ромба через две диагонали:

a = √ d 1 2 + d 2 2 2
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

a = d 1 √ 2 + 2 cosα

a = d 2 √ 2 — 2 cosβ
6. Формула стороны ромба через большую диагональ и половинный угол:

a = d 1 2 cos ( α /2)

a = d 1 2 sin ( β /2)
7. Формула стороны ромба через малую диагональ и половинный угол:

a = d 2 2 cos ( β /2)

a = d 2 2 sin ( α /2)
8. Формула стороны ромба через периметр:

a = Р 4

Диагонали ромба

Формулы определения длины диагонали ромба:

d 1 = a √ 2 + 2 · cosα

d 1 = a √ 2 — 2 · cosβ

d 2 = a √ 2 + 2 · cosβ

d 2 = a √ 2 — 2 · cosα

d 1 = 2 a · cos ( α /2)

d 1 = 2 a · sin ( β /2)

d 2 = 2 a · sin ( α /2)

d 2 = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

S = 1 d 1 d 2 2

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

S = 1 d 1 2 · tg ( α /2) 2

S = 1 d 2 2 · tg ( β /2) 2

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Периметр любой плоской геометрической фигуры равен сумме длин всех её сторон. Так как у прямоугольника, квадрата и ромба 4 стороны, то их периметры можно находить последовательным сложением четырёх длин, которым равны их стороны.

Рассмотрим нахождение периметра, с помощью последовательного сложения на примере трёх четырёхугольников:

Как найти периметр ромба

Прямоугольник имеет две стороны по 3 см и две стороны по 5 см, значит его периметр можно найти так:

P = AB + BC + CD + DA = 3 см + 5 см + 3 см + 5 см = 16 см.

Квадрат и ромб имеют по 4 одинаковых стороны, значит их периметр будет равен сумме 4 одинаковых длин:

P = A1B1 + B1C1 + C1D1 + D1A1 = 3 см + 3 см + 3 см + 3 см = 12см — для квадрата;

P = A2B2 + B2C2 + C2D2 + D2A2 = 3 см + 3 см + 3 см + 3 см = 12 см — для ромба.

Так как в каждом из данных четырёхугольников есть повторяющиеся длины (относящиеся к равным по длине сторонам), то находить периметр можно не только с помощью сложения, но и заменять одинаковые слагаемые их произведением.

Рассмотрим, сначала, изменения в нахождении периметра для прямоугольника:

P = 3 см + 5 см + 3 см + 5 см = 3 см · 2 + 5 см · 2 = (3 см + 5 см)2 = 8 см · 2 = 16 см.

Из этого примера можно сделать вывод, что периметр прямоугольника равен сумме его смежных сторон, умноженной на 2.

Общая формула периметра прямоугольника:

P = (a + b)2,

где P — это периметр прямоугольника, а a и b — его смежные стороны.

Теперь рассмотрим нахождение периметра для квадрата и ромба, с заменой одинаковых слагаемых их произведение:

P = 3 см + 3 см + 3 см + 3 см = 3 см · 4 = 12 см.

Это значит, что периметр квадрата или ромба равен длине его стороны умноженной на 4.

Общая формула периметра квадрата и ромба:

P = a · 4,

где P — это периметр квадрата или ромба, а a — любая из четырёх сторон.

Источник

Содержание:

  • Определения
  • Формулы периметра основных геометрических фигур

Определения

Определение

Периметр — общая длина границы фигуры, которая чаще всего находится на плоскости.

Периметр имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Чаще всего этот термин применяется к треугольнику и многоугольникам и в этом случае означает сумму длин всех сторон фигуры.
То есть периметр — это сумма длин сторон какой-либо геометрической фигуры.

Определение

Полупериметр — половина периметра. Употребляется в основном в геометрии треугольника.

Формулы периметра основных геометрических фигур

Периметр треугольника

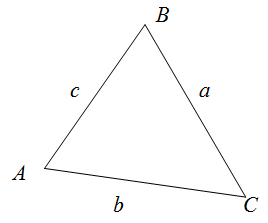
Чтобы найти периметр треугольника $ABC$,
необходимо сложить длины всех его сторон.

$$P_{Delta A B C}=a+b+c$$

Читать дальше: формула периметра треугольника и примеры решений →

Периметр круга

Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.

Для нахождения длины окружности можно использовать одну из формул

Читать дальше: формула периметра круга и примеры решений →

Периметр квадрата

Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.

$$P_{Delta A B C D}=a+a+a+a=4 a$$

Читать дальше: формула периметра квадрата и примеры решений →

Периметр прямоугольника

Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.

$$P_{Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$

Читать дальше: формула периметра прямоугольника и примеры решений →

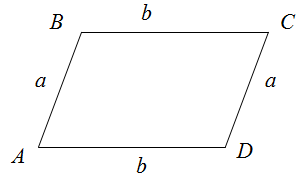
Периметр параллелограмма

Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.

$$P_{Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$

Читать дальше: формула периметра параллелограмма и примеры решений →

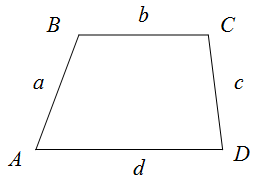
Периметр трапеции

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

$$P_{Delta A B C D}=a+b+c+d$$

Читать дальше: формула периметра трапеции и примеры решений →

Периметр ромба

Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.

$$P_{Delta A B C D}=a+a+a+a=4 a$$

Читать дальше: формула периметра ромба и примеры решений →

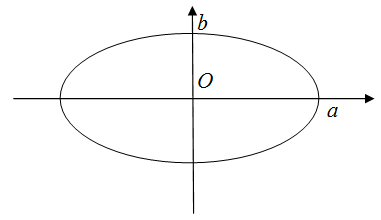
Периметр эллипса

Чтобы найти периметр эллипса
$frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$, нужно воспользоваться формулой

$$P=4 cdot frac{pi a b+(a-b)}{a+b}$$

Читать дальше: формула периметра эллипса и примеры решений →

  • Как найти периметр треугольника
  • Как найти периметр трапеции
  • Как найти периметр ромба
  • Как найти периметр эллипса
  • Как найти периметр многоугольника
  • Как найти периметр прямоугольного треугольника
  • Как найти периметр равнобедренного треугольника
  • Как найти периметр равностороннего треугольника
  • Как найти периметр круга
  • Как найти длину окружности
  • Как найти периметр квадрата
  • Как найти периметр прямоугольника
  • Как найти периметр параллелограмма
Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как по номеру лицензии найти организацию по
  • Как найти ctg2a если известен tga
  • Как составить климат градусов
  • Как в автокаде найти шрифт по
  • Как найти стим в сбербанке

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии