Как найти периметр параллелограмма с биссектрисой угла

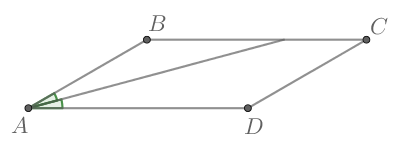
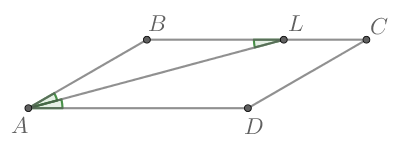
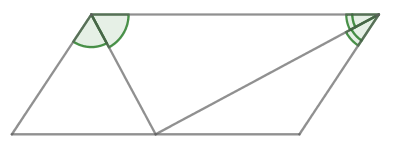
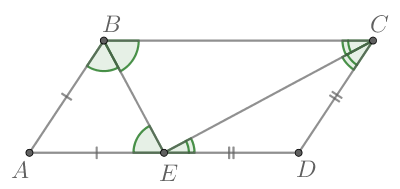
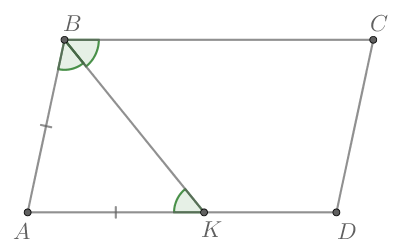
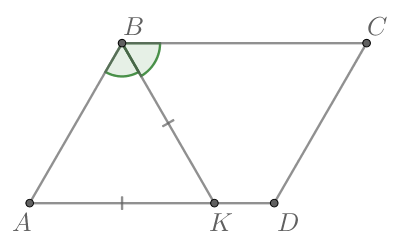
Построим параллелограмм ABCD и проведем биссектрису угла А.

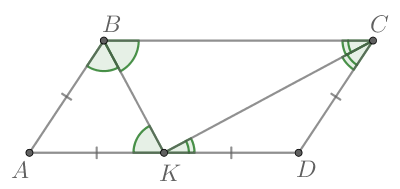
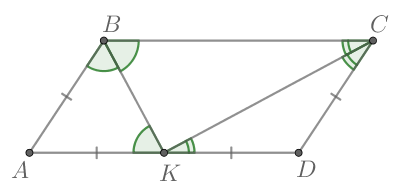
Углы BKA и KAD равны, т.к. являются накрест лежащими углами при параллельных прямых. Углы BAK и KAD также равны (биссектриса делит угол пополам). Соответственно, угла BAK и BKA также равны. Соответственно, треугольник BAK является равнобедренным.

Сторона AB=BK=15 см. ВС = ВК+КС= 15+9=24 см.

Периметр — это сумма длин всех сторон. В параллелограмме параллельные друг другу стороны равны между собой.

Соответственно, периметр параллелограмма равен 15+15+24+24 = 78 см

Источник

Биссектриса угла параллелограмма делит пересекаемую ею сторону на отрезки в 4 и 5 см. Найдите периметр параллелограмма.

Спрятать решение

Решение.

Возможно два случая:

а)  Биссектриса отсекает равнобедренный треугольник с боковыми сторонами, равными 5 см. Тогда различные стороны параллелограмма будут равны 5 см и 9 см. Периметр параллелограмма в этом случае равен 28 см.

б)  Биссектриса отсекает равнобедренный треугольник с боковыми сторонами, равными 4 см. Тогда различные стороны параллелограмма будут равны 4 см и 9 см. Периметр параллелограмма в этом случае равен 26 см.

Ответ: 28 см или 26 см.

Источник

Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.

Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.

Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».

Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.

Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

Источник

ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

похожие вопросы 5

Источник

Тема 1.

Геометрия на плоскости (планиметрия)

1

.

07

Параллелограмм и свойство его биссектрисы

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

Решаем задачи

Показать ответ и решение

Так как AK — биссектриса, то ∠BAK = ∠KAD.

Из параллельности сторон AD и BC ∠KAD = ∠BKA.

Тогда ∠BKA = ∠BAK, а значит ABK — равнобедренный, AB = BK =7.

BC =BK + KC = 7+ 12= 19

Периметр параллелограмма равен удвоенной сумме соседних сторон:

P = 2(AB + BC )= 2(7 +19)= 2⋅26 =52

Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный ∘ 15 . Ответ
дайте в градусах.

PIC

Показать ответ и решение

PIC

Пусть биссектрисса пересекает сторону BC в точке L. По условию ∘ ∠ALB = 15 . Так как ABCD — параллелограмм,
прямые BC и AD параллельны, а значит

∠LAD = ∠BLA = 15∘

Так как AL — биссектриса, то

∘ ∘ ∠BAD = 2∠LAD = 2⋅15 = 30

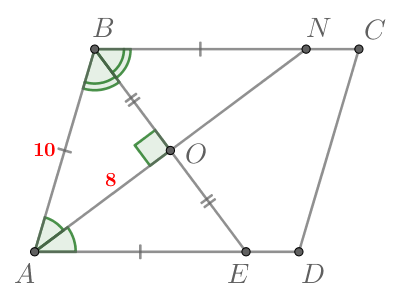
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной
стороне. Меньшая сторона параллелограмма равна 6. Найдите его большую сторону.

PIC

Показать ответ и решение

По условию ∠ABE = ∠EBC. Противоположные сторолны параллелограмма BC ∥AD, следовательно, ∠EBC =∠BEA.
Тогда в треугольнике AEB углы B и E равны, значит, он равнобедренный, то есть

AB = AE = 6

PIC

Из полностью аналогичных соображений

DE = DC = 6

Тогда большая сторона параллелограмма равна

AD = AE + DE = 12

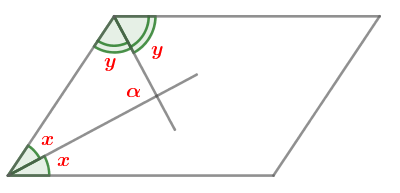
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

PIC

Показать ответ и решение

Проведем биссектрисы двух соседних углов. Пусть они разбили первый угол на два угла, равных x, второй угол — на два угла,
равных y. Нужно найти α.

PIC

По свойству параллелограмма сумма его углов, прилежащих к одной стороне, равна 180∘. Следовательно,

∘ ∘ 2x +2y = 180 ⇔ x +y = 90

Так как сумма углов в треугольнике равна 180∘, то

∘ ∘ ∘ ∘ ∘ x +y +α = 180 ⇒ α= 180 − (x + y) =180 − 90 = 90

Показать ответ и решение

PIC

По свойству биссектрисы параллелограмма △ABE и △ABN — равнобедренные, то есть AE = AB = BN. Следовательно,
AO — биссектриса, проведенная к основанию, значит, высота, то есть ∠AOB = 90∘, а также и медиана, то есть
BO =OE.

Аналогично AO = ON = 12AN = 8. Тогда по теореме Пифагора из △AOB :

∘ ---2----2- BO = AB − AO =6 ⇒ BE = 2⋅6= 12

Показать ответ и решение

PIC

По свойству биссектрисы параллелограмма △ABK и △CDK — равнобедренные (AB = AK, CD = DK ). Следовательно,

BC = AD = AK +DK = AB + CD = 2AB = 8

Показать ответ и решение

∘ ∘ ∠ABK = ∠BKA = 60 ⇒ ∠BAD = 60

Значит, △ABK — равносторонний, тогда

AB = BK =3 ⇒ PABCD = 2⋅3+ 2⋅5= 16

Показать ответ и решение

∠ABK = ∠KBC, так как BK — биссектриса ∠ABC. ∠KBC = ∠BKA, так как это накрест лежащие углы при параллельных
прямых. Тогда:

1 ∘ 1 ∘ ∘ ∘ ∠ABK = ∠BKA = 2(180 − ∠BAD )= 2(180 − 60 )= 60

△ABK равносторонний, значит AB = BK = AK =6. Тогда

AK :KD = 6:KD = 3:2 ⇒ KD = 4

AD = AK +KD = 10

Тогда

PABCD = 2 ⋅6 +2 ⋅10 = 32

Показать ответ и решение

В равнобедренном треугольнике ABN углы при основании равны, тогда

∠BAN = ∠BNA = 1(180∘− 150∘)= 15∘ 2

Поскольку накрест лежащие углы при параллельных прямых AD и BC и секущей AN равны, то

∠NAD = ∠BNA = 15∘

Показать ответ и решение

Так как внутренние накрест лежащие углы при параллельных прямых и секущей равны, то ∠BNA = ∠NAD.

Так как AN — биссектриса, то ∠NAD = ∠BAN, откуда получаем ∠BNA = ∠BAN.

Таким образом, треугольник ABN — равнобедренный, BN = AB, тогда

BC = BN + NC = 5+ 3 =8

В итоге, периметр параллелограмма ABCD равен

8+ 8+ 5+ 5= 26

Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне.
Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

PIC

Показать ответ и решение

PIC

AB= 5. Так как в параллелограмме противоположные стороны параллельны, то ∠AKB =∠KBC как накрест лежащие при
AD ∥BC и секущей BK. Следовательно, ∠AKB = ∠ABK, то есть △ABK равнобедренный:

AK = AB

Аналогично

DC = DK

Так как в параллелограмме противоположные стороны равны, то

AK = AB = 5 =CD = DK

Следовательно, AD = 5+ 5 =10 — большая сторона.

Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла.
Найдите большую сторону параллелограмма, если его периметр равен 88.

PIC

Показать ответ и решение

PIC

Из условия задачи следует, что AK :KD = 4:3. Обозначим AK = 4x, KD =3x. Следовательно, AD = 7x.

Так как в параллелограмме противоположные стороны параллельны, то ∠AKB =∠KBC как накрест лежащие при AD ∥BC
и секущей BK. Следовательно, ∠AKB = ∠ABK, то есть △ABK равнобедренный:

AK = AB ⇒ AB = 4x

Так как противоположные стороны параллелограмма равны, то

88 = 2(4x+ 7x) ⇒ x =4

Значит, большая сторона параллелограмма равна

7x= 28

Показать ответ и решение

∠AOB = 90∘, следовательно, OM = 1 ⋅AB, 2 т.к. в прямоугольном треугольнике медиана, проведенная из прямого угла, равна
половине гипотенузы. Тогда

AB = 2⋅4= 8 ⇒ PABCD = 2⋅8 +2 ⋅10 = 36

Показать ответ и решение

△CKL = △BKA и являются равнобедренными.

AB = CL =3 BC = BK + KC = 2 ⋅CK = 2⋅CL = 2⋅3= 6

Тогда

PABCD = 2⋅3+ 2⋅6= 18

PIC

В параллелограмме ABCD : BK — биссектриса, BK = AK. Чему равен ∠D?

Показать ответ и решение

Т.к. биссектриса отсекает равнобедренный треугольник от параллелограмма, то AK = AB. Значит △ABC равносторонний, то
есть

∘ ∘ ∘ ∘ ∠A = 60 ⇒ ∠D = 180 − 60 = 120

Показать ответ и решение

Внутренние накрест лежащие углы при параллельных прямых и секущей равны, тогда ∠BNA = ∠NAD, но ∠NAD = ∠BAN,
тогда ∠BNA = ∠BAN и треугольник BAN — равнобедренный, AB = BN. Обозначим AB = x.

Аналогично треугольник MCD — равнобедренный, x= CD = MD.

BC = 2x =AD ⇒ NC = x= AM = BN

AM ∥BN, тогда ABNM — параллелограмм, откуда заключаем, что

MN = AB = 4

В параллелограмме ABCD проведены биссектрисы AN и BM, ∠ABM = 58∘. Найдите ∠BAN. Ответ дайте в градусах.

PIC

Показать ответ и решение

Сумма односторонних углов при параллельных прямых и секущей равна 180∘, тогда

∘ ∠DAB + ∠ABC = 180

Так как AN и BM — биссектрисы, то

∘ ∠BAN + ∠ABM = 0,5(∠DAB + ∠ABC )= 90

∠ABM = 58∘, тогда

∠BAN = 90∘ − 58∘ =32∘

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти доверия к нему
  • Как исправить в icq
  • Как найти долг по коммунальным платежам
  • Как найти противолежащий катет если известен угол
  • Сода как найти в турции

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии