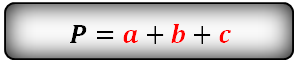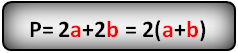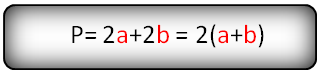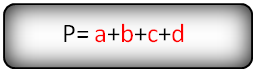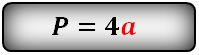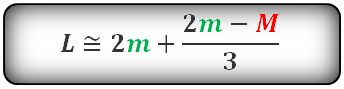Периметр круга
- Главная
- /
- Математика
- /
- Геометрия
- /
- Периметр круга
Чтобы посчитать периметр круга просто воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
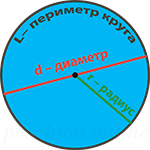
Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.
Ликбез: Круг — часть плоскости, лежащая внутри окружности.
Как посчитать периметр круга зная радиус
Чему равен периметр круга если
его радиус ?
Ответ:
0
Каков периметр круга (L) если его радиус r ?
Формула
L = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная диаметр
Чему равен периметр круга если
его диаметр ?
Ответ:
0
Каков периметр круга (L) если его диаметр d?
Формула
L = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная его площадь
Чему равен периметр круга если
его площадь ?
Ответ:
0
Каков периметр круга (L) если его площадь S?
Формула
L = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 8 см2, то его периметр ≈ 10 см.
См. также
При помощи нашего калькулятора вы легко сможете узнать периметр круга или длину окружности.
Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.
Длина окружности всегда равна числу π (Пи)
Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…
Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.
Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».
Иными словами Пи ≈ 3,14 диаметрам круга или окружности.
Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна
P = D * π
или
P = 2 πR
где R –это радиус, а D – это диаметр
Периметром фигур является длина их пограничных линий. Знание периметра требуется в различных практических ситуациях. Периметр фигур тесно связан с определением их площади.
Общей формулы для вычисления периметров различных фигур не существует, по этой причине на странице предлагается набор онлайн калькуляторов, позволяющий вычислять данный параметр для основных геометрических фигур. Наличествуют программы вычисления длин окружности и дуги.
Пользоваться калькуляторами очень легко, в соответствующих полях нужно задать координаты точек фигуры, значения длин сторон, радиусов или углов. При нажатии на кнопку «Вычислить» в соответствующем поле можно прочитать результат.
Программные скрипты используют при вычислении следующие формулы расчета периметров:
|
— P = 2 х π х r; — P = a + b +c; |
— P = 4 х a; — P = 2 х (a + b); |
— P = a + b + c + d; — P = n х a и др. |
В обыденной жизни чаще всего расчет периметра необходим для определения количества стройматериалов при устройстве ограждения придомового или производственного участка, площадки для автостоянки, выпаса скота и пр.
Вычислить, найти периметр геометрических фигур
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

r — радиус окружности
D — диаметр окружности
π ≈ 3.14
Формула длины окружности, (L):
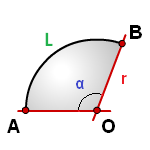
r— радиус окружности
α— угол AOB, в градусах
π ≈ 3.14
Формула длины дуги (L):
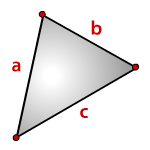
a, b, c, — стороны треугольника
Формула периметра треугольника через его стороны (P):
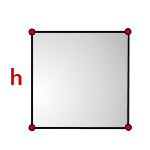
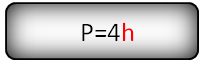
h — сторона квадрата
Формула периметра квадрата, (P):
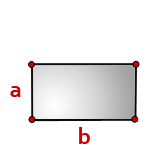
b — длина прямоугольника
a — ширина прямоугольника
Формула периметра прямоугольника, (P):
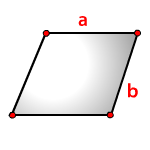
a, b — стороны параллелограмма
Формула периметра параллелограмма, (P):
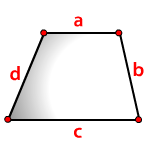
a, b, c,d — стороны трапеции
Формула периметра трапеции, (P):
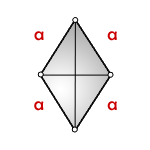
a — сторона ромба
Формула периметра ромба (P):
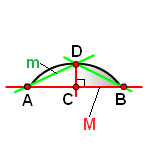
Точка С делит отрезок АВ пополам.
Углы ACD и DCB— прямые, (90°).
m— хорда AD=DB
M— хорда AB
Формула Гюйгенса, длина дуги ADB, (L):
* Погрешность для углов меньше 60°, составляет менее 0,5%
В данной публикации мы рассмотрим, что такое периметр геометрической фигуры, как он считается, а также разберем примеры для демонстрации практического применения теоретических знаний.
- Определение периметра
- Формулы периметра распространенных фигур
- Примеры нахождения периметра
Определение периметра
Периметр – это сумма длин всех сторон геометрической фигуры (треугольника, квадрата, трапеции, ромба и т.д.).
Для измерения периметра используются единицы длины: миллиметры (мм), сантиметры (см), метры (м), километры (км) и т.д.
Общепринятое обозначение периметра – это латинская буква “P“, под которой можно добавить сокращенное название фигуры или ее обозначение. Например:
- Периметр треугольника можно записать как “Pтреуг.“ или “P△“;
- Периметр квадрата – “Pквадр.“ или “P□“
Формулы периметра распространенных фигур
Периметр произвольного многоугольника находится путем сложения длин всех его сторон.
Примеры нахождения периметра
Пример 1
Найдем периметр квадрата с длиной стороны 5 см.
Pквадр. = 5 + 5 + 5 + 5 = 4 ⋅ 5 = 20 см.
Пример 2
Вычислим периметр прямоугольника с длиной 8 см и шириной 6 см.
Pпрямоуг. = 6 + 8 + 6 + 8 = (6 + 
Пример 3
Найдем периметр шестиугольника ниже.
P = AB + BC + CD + DE + EH + HA = 5 + 3 + 5 + 4 + 6 + 5 = 28.