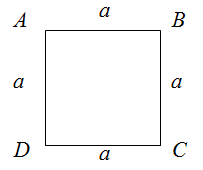Как найти периметр квадрата оформление

Памятка по решению геометрических задач.

Нахождение ПЕРИМЕТРА(Р).

Правило

Периметр – это сумма длин сторон какой-нибудь геометрической

фигуры.

Кратко будем обозначать геометрические понятия следующим образом:

Р пр – это периметр прямоугольника;

Р кв — это периметр квадрата;

а — это длина большей стороны фигуры;

в — это ширина стороны фигуры (иногда буква может меняться на

любую другую )

Нахождение периметра прямоугольника (Рпр ) можно находить

3 способами: Рпр = а+в+а+в (этот способ применяется, когда нужно найти

периметр любой другой геомет. фигуры)

Рпр = а ∙ 2+в ∙ 2;

Рпр = (а+в) ∙ 2 (этим способом мы будем пользоваться чаще!)

2. Нахождение сторон прямоугольника (а или в)

а = Рпр : 2 – в:

в = Рпр : 2 – а

Нахождение периметра квадрата (Ркв) по формуле:

Ркв = а ∙ 4

Нахождение стороны квадрата (а)

а = Ркв : 4

Оформление задачи в тетради

Например :

Дано: а

а = 5см

в = 3см в

Рпр — ?

(если нужно начертить чертёж, то его нужно чертить на этом месте, а

решение начинать с середины листа, а если не требуется начертить

чертёж, то решение выполнять нужно на этом месте )

Решение.

Рпр = (а+в) ∙ 2

Рпр = (5см +3см) ∙ 2 = 16 (см)

Ответ: Рпр = 16 см

(Аналогично выполняются подобные задачи геометрического характера.)

Нахождение ПЛОЩАДИ(S).

Правило

Площадь – это внутренняя часть какой-нибудь геометрической фигуры.

Кратко будем обозначать геометрические понятия следующим образом:

Sпр – это площадь прямоугольника;

Sкв — это площадь квадрата;

а — это длина большей стороны фигуры;

в — это ширина стороны фигуры (иногда буква может меняться на

любую другую )

Нахождение площади прямоугольника (Sпр ) по формуле:

Sпр = а ∙ в

Нахождение сторон прямоугольника (а или в):

а = Sпр: в;

в = Sпр:а

3.Нахождение площади квадрата (Sкв) по формуле:

Sкв = а ∙ а

4.Нахождение стороны квадрата (а)

а = Sкв : а

Оформление задачи в тетради

Например: ( данные могут быть разные, но оформление одинаковое)

Дано: Решение.

а = 5см Sпр = а ∙ в

Sпр = 15см2 в = Sпр: а

в — ? см в = 15см2 : 5 см = (3 см)

Рпр -?см Рпр = (а+в) ∙ 2

Рпр = (5см + 3 см) ∙ 2 = 16 (см)

Ответ: в = 3 см; Рпр = 16 см

5.Нахождение площади прямоуг.треугольника (Sтр) по формуле:

Sтр. = (а ∙ в):2

Источник

Загрузить PDF

Периметр двумерной фигуры – это общая длина ее границы, равная сумме длин сторон фигуры.^[1] Квадрат – это фигура с четырьмя сторонами одинаковой длины, которые пересекаются под углом 90°.^[2] Так как в квадрате все стороны имеют одинаковую длину, то вычислить его периметр очень легко. Эта статья расскажет вам, как вычислить периметр квадрата по одной данной стороне, по данной площади и по данному радиусу окружности, описанной вокруг квадрата.

1

Формула для вычисления периметра квадрата: P = 4s, где s – длина стороны квадрата.
2
Определите длину одной стороны квадрата и умножьте ее на 4, чтобы найти периметр. Чтобы определить длину стороны, измерьте ее линейкой или посмотрите ее значение в учебнике (задаче). Вот некоторые примеры вычисления периметра:
- Если сторона квадрата равна 4, то P = 4 * 4 = 16.
- Если сторона квадрата равна 6, то P = 4 * 6 = 36.
Реклама

1

Формула для вычисления площади квадрата. Площадь любого прямоугольника (а квадрат – это частный случай прямоугольника) равна произведению его длины на его ширину.^[3] Поскольку длина и ширина квадрата равны, то его площадь вычисляется по формуле: A = s*s = s², где s – длина стороны квадрата.
2
Извлеките квадратный корень из значения площади, чтобы найти сторону квадрата. Для этого в большинстве случаев воспользуйтесь калькулятором (введите значение площади и нажмите клавишу «√»). Вы также можете вычислить квадратный корень вручную.
- Если площадь квадрата равна 20, то его сторона равна: s = √20 = 4,472.
- Если площадь квадрата равна 25, то s = √25 = 5.
3
Умножьте найденную сторону на 4, чтобы найти периметр. Вычисленное значение стороны подставьте в формулу для нахождения периметра: P = 4s. Вы найдете периметр квадрата.
- В нашем первом примере: P = 4 * 4,472 = 17,888.
- Периметр квадрата, площадь которого равна 25, а сторона равна 5, равен Р = 4 * 5 = 20.
Реклама

1

Вписанный квадрат – это квадрат, вершины которого лежат на окружности.^[4]
2

Отношение между радиусом окружности и длиной стороны квадрата. Расстояние от центра описанной окружности до вершины вписанного в нее квадрата равно радиусу окружности. Чтобы найти сторону квадрата s, необходимо диагональю разделить квадрат на 2 прямоугольных треугольника. Каждый из этих треугольников будет иметь равные стороны a и b и общую гипотенузу с, равную удвоенному радиусу описанной окружности (2r).
3
Воспользуйтесь теоремой Пифагора, чтобы найти сторону квадрата. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами а и b и гипотенузой с: a² + b² = c².^[5] Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r, то мы можем переписать и упростить это уравнение:
- a² + a² = (2r)²«‘; теперь упростим это уравнение:
- 2a² = 4(r)²; теперь разделим обе стороны уравнения на 2:
- (a²) = 2(r)²; теперь извлечем квадратный корень из обеих сторон уравнения:
- a = √(2r). Таким образом, s = √(2r).
4

Умножьте найденную сторону квадрата на 4, чтобы найти его периметр. В этом случае периметр квадрата: P = 4√(2r). Эту формулу можно переписать так: Р = 4√2 * 4√r = 5,657r, где r – радиус описанной окружности.^[6]
5
Пример. Рассмотрим квадрат, вписанный в окружность радиусом 10. Это означает, что диагональ квадрата равна 2 * 10 = 20. Используя теорему Пифагора, мы получим: 2(a²) = 20², то есть 2a² = 400. Теперь разделим обе стороны уравнения на 2 и получим: a² = 200. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142. Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57.
- Обратите внимание, что вы могли бы получить тот же результат, просто умножив радиус (10) на 5,657: 10 * 5,567 = 56,57; но такой метод трудно запомнить, поэтому лучше пользоваться процессом вычисления, описанным выше.
Реклама

Об этой статье

Эту страницу просматривали 413 196 раз.

Была ли эта статья полезной?

Источник

Perimeter of square is defined as the total length of the boundaries of that square. The perimeter of any shape can be obtained in the same pattern, that is, finding the total length of the shape’s boundary. A square is a closed regular polygon where all sides are equal, and all angles are 90° each. Square is a special type of quadrilateral as all four sides, angles, and diagonals are equal, also diagonals bisect each other at a right angle. Since all the sides of the square are equal, the perimeter of the square can be obtained by adding all the sides or by multiplying one side by 4.

What is Perimeter of Square?

The perimeter of any closed geometrical shape is obtained by finding the total length of the boundaries of its shape. Perimeter is the length that outlines the shape of the 2-D figures. The 2D figures include squares, rectangles, triangles, circles, and other polygons. For 2-D shapes, perimeter, and area is considered general calculations, and for 3-D shapes and forms surface area and volume is considered general calculation. The perimeter can be found for irregular shapes as well. Some of the commonly used terms with respect to 2-D shapes are as follows:

Vertices: They are the endpoints of a shape.
Edge/Side: A line segment joining two adjacent vertices.
Diagonals: A line segment joining two nonadjacent vertices.
Area: Area is the space occupied by a figure.
Perimeter: The perimeter is the total length of the boundary of the figure.
Angles: The point where two sides meet is the angle often measured in degrees or radians.

Perimeter of Square Formula

The perimeter of the Square can be calculated using the side length of the square. If the side of the square is represented as “a”, the formula for perimeter of square can be expressed as,

As shown above, the perimeter of a square is 4 times the length of its sides as all sides are equal in a square. The unit for the perimeter of a square is the unit used for length. It is measured in meters (m), centimeters (cm), inches (in), etc.

Example: Calculate the perimeter of a square having a side of 8cm.

Solution:

Perimeter of square = 4 × side

⇒ P = 4 × 8

⇒ P = 32 cm.

Derivation of Perimeter of Square

In order to find the perimeter of closed geometrical shape, the length of all the boundaries should be added. Similarly, to derive the perimeter of the square, we are required to add all the sides of the square, assume the length of the sides is denoted as “a”,

Perimeter = a + a + a + a

⇒ Perimeter of square = 4a

Where a is the side of the square.

How to Find the Perimeter of a Square?

Perimeter is the length of the boundary. It is often known as the distance around a closed 2D figure. The perimeters can be different according to the shapes given. The perimeter of a square can be calculated using side length, and there are cases when the side length is not given, then the perimeter of square can be obtained using diagonal and area. Therefore, the perimeter of square can be calculated using three methods,

Using side length
Using diagonal
Using area

Perimeter of Square using Side Length

The below-given steps can be used to find the perimeter of square using side length,

Measure the side of the square.
Multiply the side length by 4.
Express the perimeter obtained in the respective unit.

Perimeter of Square using Diagonal

However, if the side of the square is not given, but the diagonal is given, then the formula becomes,

Therefore, the Perimeter of square is,

The below-given steps can be used to find the area of the perimeter of the square using diagonals,

Measure the diagonal of the square.
Calculate the perimeter of the square using the formula, P = 4 × (Diagonal/√2).

Example: Find the perimeter of the diagonal is 4√2 m.

Solution:

The Perimeter of square is,

P = 4 × (Diagonal/√2)

⇒ P = 4 × (4√2/√2)

⇒ P = 16 m

Perimeter of Square using Area

When the area of square is given, let us assume the area of square is a. As we all know, Area = (side)²

Therefore, the perimeter of the square is,

The below-given steps can be used to find the area of the perimeter of square using area,

Measure the area of the square.
Calculate the area of the square using the formula, Perimeter = 4 × √Area.

Example: Find the perimeter if the area of the square is 49 square units.

Solution:

The Perimeter of square is,

P = 4 × √Area

⇒ P = 4 × √49

⇒ P = 28 units

Solved Examples on Perimeter of Square

Example 1: Find the perimeter of the square if the side given is 4 units.

Solution:

The Perimeter of square is,

P = 4 × side

⇒ P = 4 × 4

⇒ P = 16 units

Example 2: Find the side and perimeter of the square if the diagonal given is 2√2 cm.

Solution:

Side = Diagonal/√2

⇒ Side = 2√2/√2

⇒ Side = 2 cm

Perimeter of square = 4×side

⇒ Perimeter = 8 cm

Example 3: Find the side of the perimeter of the given square is √2.

Solution:

Perimeter = side × 4

⇒ √2 = side × 4

Therefore, Side = √2/4

Example 4: Find the diagonal if the perimeter of the square is 3√2 cm.

Solution:

Perimeter = 4 × (diagonal/√2)

⇒ (3√2 × √2 ) /4 = diagonal

⇒ Diagonal = 1.5 cm

Example 5: Find the perimeter if the area given is 25 sq units.

Solution:

Perimeter = 4√Area

⇒ Perimeter = 4√25

⇒ Perimeter = 20 units

Example 6: Find the area and perimeter of the square if its side is 3 units.

Solution:

Perimeter = 4×side

⇒ Perimeter = 4 × 3

⇒ Perimeter = 12 units

Area = (Side)²

⇒ Area = (3)²

⇒ Area = 9 sq units

FAQs on Perimeter of Square

Question 1: What is the perimeter of the square formula?

Answer:

The perimeter of square is defined as the total length of its boundaries. The formula for perimeter of square is,

P = 4 × Side.

Question 2: What is the unit of the perimeter of square?

Answer:

The units used for perimeter of square is the units used for length. The units used are meter (m), centimeter (cm), inches (in), etc.

Question 3: What is the area and perimeter of square?

Answer:

The perimeter of square is defined as the total length of its boundaries. The formula for perimeter of square is,

P = 4 × Side.

The space covered in 2-dimensional space by the square is called as area of a square. The formula used for area of square is,

A = Side²

Question 4: How to find the side length of the square when perimeter is given?

Answer:

In order to find the side length of square, first note down the formula for perimeter of square.

P = 4 × Side

Side = P/4

Hence, to find side length of square when perimeter is given, divide the perimeter by 4.

Perimeter of Rectangle

Perimeter of Triangle

Circumference of a Circle

Источник

Пример:

измеряя с помощью линейки длины сторон прямоугольника, получим (2) см и (4) см. Противолежащие им стороны имеют такую же длину — (2) см и (4) см.

Найдём сумму длин всех сторон этого прямоугольника.

Для этого сложим все эти длины.

Получим:

(2) см (+) (4) см (+) (2) см (+) (4) см (=) (12) см.

Периметр — это сумма длин всех сторон фигуры.

Значит,

складывая длины всех сторон прямоугольника, получаем периметр прямоугольника.

Периметр обозначается заглавной латинской буквой (Р).

Итак,

периметр прямоугольника (Р = 12) см.

Найдём периметр треугольника.

Сначала измерим стороны треугольника.

Длины сторон треугольника равны (4) см, (3) см, (6) см.

Значит,

сумма длин всех сторон треугольника, т. е. периметр треугольника

равен:

(Р) (=) (3) см (+) (4) см (+) (6) см (=) (13) см.

Дан квадрат, длина стороны которого равна (4) см.

У квадрата все стороны равны.

Периметр квадрата равен сумме длин всех сторон квадрата.

Получим:

(Р) (=) (4) см (+) (4) см (+) (4) см (+) (4) см (=) (16) см.

Если у треугольника все стороны равны, такой треугольник называется равносторонний.

Для определения периметра данного треугольника найдём сумму длин всех его сторон.

Получим:

(Р) (=) (5) см (+) (5) см (+) (5) см (=) (15) см.

Источники:

Источник

Содержание:

Формула
Примеры вычисления периметра квадрата

Формула

Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.

По определению, квадрат — это правильный четырехугольник, у которого все углы и стороны равны. Тогда, если задан квадрат
$ABCD$ со стороной
$a$, то для него формула для нахождения периметра примет вид:

$$P_{Delta A B C D}=a+a+a+a=4 a$$

Примеры вычисления периметра квадрата

Пример

Задание. Дан квадрат
$ABCD$ со стороной
$a=0,25$ см. Вычислить периметр заданного квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой

$$P_{Delta A B C D}=4a$$

Подставляя в неё значение 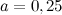, получим:

$P_{Delta A B C D}=4 cdot 0,25=1$ (см)

Ответ. $P_{Delta A B C D}=1$ (см)

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

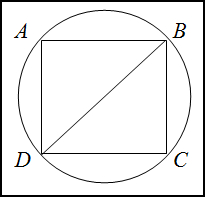
Задание. Найти периметр квадрата
$ABCD$, который вписан в окружность радиуса
$r=2$ дм.

Решение. Сделаем рисунок.

Диаметр описанной окружности является диагональю вписанного в неё квадрата, то есть

$DB=d=2r=2 cdot 2=4$ (дм)

Известно, что сторона квадрата $AB$ связана с его диагональю
$DB$ соотношением:

$$D B=A B sqrt{2}$$

Откуда получаем, что

$A B=frac{D B}{sqrt{2}}=frac{4}{sqrt{2}}=2 sqrt{2}$ (дм)

А тогда искомый периметр:

Ответ. $P_{Delta A B C D}=8 sqrt{2}$ (дм)

Читать дальше: как найти периметр прямоугольника.

Источник

Похожие статьи

Об этой статье

Была ли эта статья полезной?

What is Perimeter of Square?

Perimeter of Square Formula

Derivation of Perimeter of Square

How to Find the Perimeter of a Square?

Perimeter of Square using Side Length

Perimeter of Square using Diagonal

Perimeter of Square using Area

Solved Examples on Perimeter of Square

FAQs on Perimeter of Square

Question 1: What is the perimeter of the square formula?

Question 2: What is the unit of the perimeter of square?

Question 3: What is the area and perimeter of square?

Question 4: How to find the side length of the square when perimeter is given?

Read More

Формула

Примеры вычисления периметра квадрата

Не пропустите также: