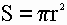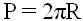Как найти периметр контура - AvtoShod.ru - решение различных проблем

The contours of the objects in an image are very helpful to compute the area and perimeter of the image. A contour of an image is a curve joining all the continuous points along the boundary, having the same color or intensity. Contours are used for shape analysis and object detection and recognition etc.

To compute the area and perimeter of an object, we first detect the contour of the object and then apply cv2.contourArea() and cv2.arcLength() functions respectively.

Syntax

The following syntax are used for the functions −

area = cv2.contourArea(cnt)
perimeter = cv2.arcLength(cnt, True)

Where, «cnt» is a numpy array of the contour points of an object in the image.

Steps

You can use the following steps to compute the area and perimeters of the contours in an image −

Import the required library. In all the following Python examples, the required Python library is OpenCV. Make sure you have already installed it.

import cv2

Read the input image using cv2.imread() and convert it to grayscale.

img = cv2.imread('pentagon.png')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

Apply thresholding on the grayscale image to create a binary image.

ret,thresh = cv2.threshold(gray,150,255,0)

Find the contours in the image using cv2.findContours() function.

contours, _ = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

Compute the area and perimeters for the detected contours in the image using cv2.contourArea(cnt) and cv2.arcLength(cnt, True) functions.

area = cv2.contourArea(cnt)
perimeter = cv2.arcLength(cnt, True)

Draw the contours on the input image.

cv2.drawContours(img, [cnt], -1, (0,255,255), 3)

Print the area and perimeters of the detected contours in the image.

print('Area:', area)
print('Perimeter:', perimeter)

Let’s have a look at some examples for a better understanding.

Example 1

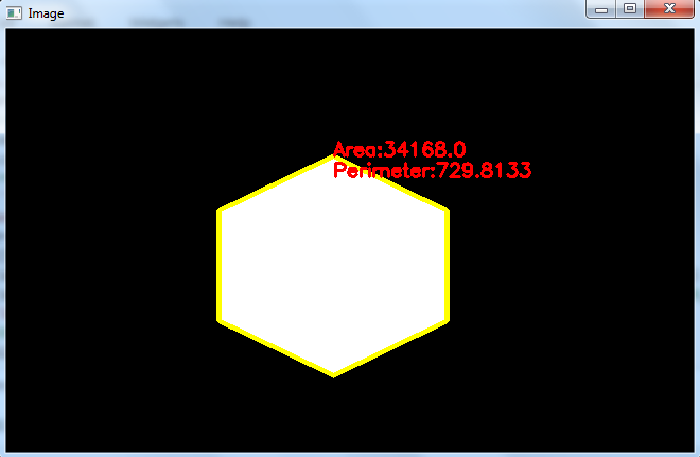
In this program, we compute the area and perimeter of detected contour in the input image ‘pentagon.png‘.

import cv2


img = cv2.imread('pentagon.png')


gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)


ret,thresh = cv2.threshold(gray,150,255,0)


contours,hierarchy = cv2.findContours(thresh, cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)
print("Number of contours in image:",len(contours))
cnt = contours[0]


area = cv2.contourArea(cnt)
perimeter = cv2.arcLength(cnt, True)
perimeter = round(perimeter, 4)
print('Area:', area)
print('Perimeter:', perimeter)
img1 = cv2.drawContours(img, [cnt], -1, (0,255,255), 3)
x1, y1 = cnt[0,0]
cv2.putText(img1, f'Area:{area}', (x1, y1), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 0, 255), 2)
cv2.putText(img1, f'Perimeter:{perimeter}', (x1, y1+20), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 0, 255), 2)

cv2.imshow("Image", img)
cv2.waitKey(0)
cv2.destroyAllWindows()

We will use the following image as the Input File in the above program.

Output

Running the above code gives us the following output −

Number of contours in image: 1 
Area: 39738.5 
Perimeter: 787.0265

And we get the following window, showing the output −

Example 2

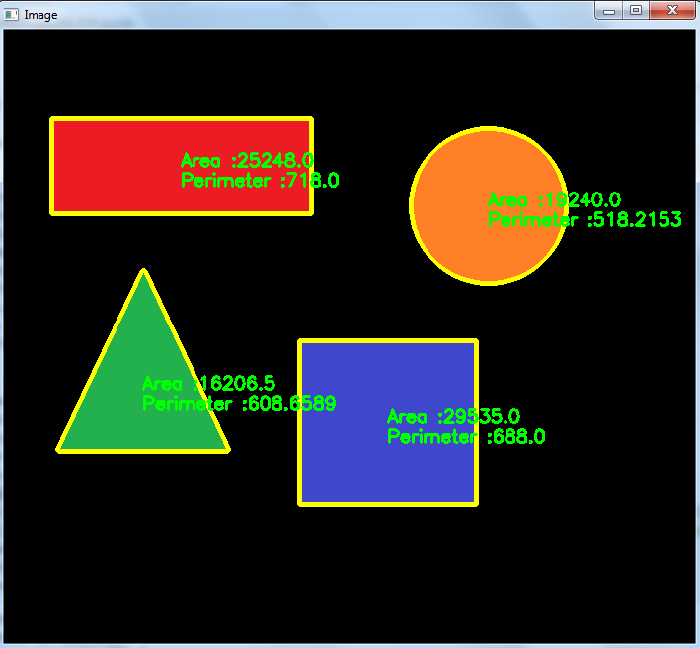
In the below program, we compute the area and perimeter for the contours in the image. We detect four contours in the image ‘shapes.jpg‘.

import cv2
import numpy as np

img1 = cv2.imread('shapes.jpg')
img = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
ret,thresh = cv2.threshold(img,10,255,0)
contours,hierarchy = cv2.findContours(thresh, 1, 2)
print("Number of contours in image:",len(contours))

for i, cnt in enumerate(contours):
   M = cv2.moments(cnt)
   if M['m00'] != 0.0:
      x1 = int(M['m10']/M['m00'])
      y1 = int(M['m01']/M['m00'])
   area = cv2.contourArea(cnt)
   perimeter = cv2.arcLength(cnt, True)
   perimeter = round(perimeter, 4)
   print(f'Area of contour {i+1}:', area)
   print(f'Perimeter of contour {i+1}:', perimeter)
   img1 = cv2.drawContours(img1, [cnt], -1, (0,255,255), 3)
   cv2.putText(img1, f'Area :{area}', (x1, y1), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2)
   cv2.putText(img1, f'Perimeter :{perimeter}', (x1, y1+20), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2)

cv2.imshow("Image", img1)
cv2.waitKey(0)
cv2.destroyAllWindows()

We will use the following image as the Input File in the above program.

Output

On execution, it will produce the following output on the console −

Number of contours in image: 4 
Area of contour 1: 29535.0 
Perimeter of contour 1: 688.0
Area of contour 2: 16206.5 
Perimeter of contour 2: 608.6589 
Area of contour 3: 19240.0 
Perimeter of contour 3: 518.2153 
Area of contour 4: 25248.0 
Perimeter of contour 4: 718.0

And we get the following window, showing the output.

Источник

Периметр: формулы и методы вычисления длины контуров

Периметр — это длина контура, описывающего фигуру. Вычисление периметра является одной из основных задач геометрии. В этой статье мы рассмотрим несколько формул и методов, которые позволяют вычислять периметр различных фигур.

Квадрат

Периметр квадрата можно найти, умножив длину одной стороны на число сторон фигуры. Таким образом, формула для вычисления периметра квадрата имеет следующий вид:

P = a * 4

где a — длина стороны квадрата.

Прямоугольник

Периметр прямоугольника вычисляется аналогично периметру квадрата. Формула для вычисления периметра прямоугольника имеет вид:

P = (a + b) * 2

где a и b — длины сторон прямоугольника.

Треугольник

Для вычисления периметра треугольника необходимо сложить длины всех его сторон. Таким образом, формула имеет следующий вид:

P = a + b + c

где a, b и c — длины сторон треугольника.

Круг

Периметр круга называется длиной окружности. Длина окружности вычисляется по формуле:

P = 2 * π * r

где r — радиус круга, а π — число пи, которое приблизительно равно 3,14.

Многоугольник

Периметр многоугольника можно вычислить, сложив длины всех его сторон. Для многоугольника со сторонами различной длины необходимо измерить каждую сторону и сложить их. Если все стороны имеют одинаковую длину, то периметр можно найти, умножив длину одной стороны на число сторон многоугольника.

Заключение

Вычисление периметра является важной задачей, которая возникает при решении многих геометрических задач. Надеемся, что эта статья поможет вам лучше понять, как вычислять периметр различных фигур.

Источник

В предыдущем блоге говорилось о том, как находить и рисовать контуры на изображении; теперь давайте поговорим об общих особенностях этих контуров и о том, как использовать соответствующие функции в opencv.

1. cv2.contourArea(cnt， oriented = False)  # Рассчитываем площадь контура

 Описание параметра: cnt - введенное значение одиночного контура;oriented:Значение по умолчанию - false, ориентировано на региональные идентификаторы,
 Если true, функция возвращает область со знаком, знак которой зависит от направления контура.(По часовой стрелке или против часовой стрелки)。
 По этому признаку положение контура можно определить по знаку местности. Если значение по умолчанию - false, площадь возвращается как абсолютное значение..

2. cv2.arcLength(cnt， closed)   # Рассчитываем длину окружности контура

 Описание параметра: cnt - входное значение одиночного контура,закрыто означает, что форма, используемая для определения объекта,
 Закрыто (True), все еще открытая кривая(False)。 

3. cv2.aprroxPolyDP(cnt, epsilon， True)  # Используется для получения приблизительного значения контура, используйте cv2.drawCountors для операций рисования

   Описание параметра: cnt - значение входного профиля, epsilon - порог T,
   Обычно периметр контура используется как порог,TrueУказывает, что контур замкнут

4. x, y, w, h = cv2.boudingrect(cnt) # Получим ограничивающий прямоугольник

 Описание параметра: x, y, w,  h представляет координаты оси X и оси Y описывающего прямоугольника,
 Ширина и высота прямоугольника cnt представляет значение входного контура.

5.cv2.rectangle(img, (x, y), (x+w, y+h), (0, 255, 0), 2)  # Рисуем на изображении прямоугольник по координатам

 Параметр Описание:  img представляет входящую картинку, (x, y)Указывает положение верхнего левого угла, 
（x+w， y+h) означает добавление позиции правого нижнего угла, (0, 255, 0)Представляет цвет,2Указывает толщину линии

6. (x, y), radius = cv2.minEnclosingCircle(cnt) # Получить информацию о местоположении описанной окружности

 Параметр Описание: (x, y)Представляет центр описанной окружности, radius представляет радиус описанной окружности, cnt представляет входной контур

7. cv2.Cricle(img, center, radius, (0, 255, 0), 2)  # Нарисуйте круг на карте по координатам

 Параметр Описание:img представляет изображение, которое нужно нарисовать, center представляет собой центральную точку круга,
 radius представляет собой радиус круга, (0, 255, 0)Представляет цвет, 2Указывает толщину линии

1. Примерный план:

Предположим, что есть кривая A, B, есть точка C на кривой, расстояние от отрезка линии AB самое дальнее, оно записывается как d1, если d1 <T (порог, установленный вами), отрезок линии AB используется как замена кривой AB, нет Соедините AC и BC, вычислите расстояние между точкой D на линейном сегменте AC и AB и запишите его как d2, если d2 <T, используйте линейный сегмент AC вместо кривой AC, в противном случае продолжайте соединение и деление.

img = cv2.imread('contours2.png')

gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
cnt = contours[0]

draw_img = img.copy()
res = cv2.drawContours(draw_img, [cnt], -1, (0, 0, 255), 2)
cv_show(res,'res')

epsilon = 0.05*cv2.arcLength(cnt,True) 
approx = cv2.approxPolyDP(cnt,epsilon,True)

draw_img = img.copy()
res = cv2.drawContours(draw_img, [approx], -1, (0, 0, 255), 2)
cv_show(res,'res')

2. Описанный прямоугольник и описанный круг

img = cv2.imread('contours.png')

gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
cnt = contours[0]

x,y,w,h = cv2.boundingRect(cnt)
img = cv2.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2)
cv_show(img,'img')

Источник

Загрузить PDF

Периметр является длиной замкнутого контура геометрической фигуры, а площадь – это величина пространства, ограниченного этим замкнутым контуром.^[1] Такие математические величины, как площадь и периметр используются в повседневной жизни, в строительстве и в других областях.^[2] Например, для покраски стен вам необходимо знать, сколько краски вам понадобится, то есть нужно определить площадь окрашиваемой поверхности. Подобные вычисления производятся при строительстве забора или во время аналогичных видов деятельности.^[3] Заранее вычислив площадь и периметр, вы сэкономите время и деньги при покупке строительных материалов.

1
Определите форму измеряемого объекта. Периметр – это длина замкнутого контура геометрической фигуры, а для вычисления периметра фигур разной формы существуют различные формулы. Помните, что если фигура не имеет замкнутого контура, то периметр такой фигуры вычислить нельзя.
- Начните с нахождения периметра прямоугольника или квадрата (особенно, если вы делаете это впервые). Такие фигуры имеют правильную форму, что облегчает задачу нахождения их периметра.
2

Возьмите лист бумаги и нарисуйте на нем прямоугольник. Эту фигуру вы будете использовать для нахождения ее периметра. Убедитесь, что противоположные стороны прямоугольника имеют одинаковую длину.^[4]
3
Измерьте ширину прямоугольника (то есть измерьте «короткую» сторону прямоугольника). Это можно сделать при помощи линейки или рулетки. Запишите значение ширины (возле «короткой» стороны). Например, ширина прямоугольника равна 3 см.
- Если вы измеряете периметр небольшой фигуры, в качестве единиц измерения используйте сантиметры, а если больших предметов – метры.
- Помните, что противоположные стороны прямоугольника равны, поэтому нужно измерить только длину двух смежных сторон.^[5]
4
Измерьте длину прямоугольника (то есть измерьте «длинную» сторону прямоугольника). Это можно сделать при помощи линейки или рулетки. Запишите значение длины (возле «длинной» стороны).
- Например, длина прямоугольника равна 5 см.
5

Запишите соответствующие значения возле противоположных сторон. Помните, что в прямоугольнике 4 стороны, а противоположные стороны прямоугольника равны.^[6] Запишите значения длины и ширины прямоугольника (в приведенном примере 5 см и 3 см) у противоположных сторон.
6
Для вычисления периметра сложите значения всех сторон. То есть в случае прямоугольника напишите: длина + длина + ширина + ширина.
- В приведенном примере периметр равен: 3 + 3 + 5 + 5 = 16 см.^[7]
- Также вы можете воспользоваться следующей формулой: периметр прямоугольника = 2* (длина + ширина) (эта формула верна, так как в прямоугольнике две пары одинаковых сторон). В приведенном примере: (5+3)*2 = 8*2 = 16 см.
7
К разным фигурам применяйте различные формулы. Для вычисления периметра фигуры другой формы потребуется соответствующая формула. В реальной жизни для нахождения периметра предмета любой формы просто измерьте его стороны. Также вы можете воспользоваться следующими формулами для вычисления периметра стандартных геометрических фигур:
- Квадрат: периметр = 4 * сторона.
- Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
- Неправильный многоугольник: периметр равен сумме всех сторон многоугольника.
- Круг: длина окружности = 2 х π х радиус = π х диаметр. ^[8]
  - π – это число пи (константа, примерно равная 3,14). Если на вашем калькуляторе есть клавиша «π», воспользуйтесь ею для выполнения более точных вычислений.^[9]
  - Радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности.^[10]^[11]
Реклама

1
Найдите значения сторон данной вам фигуры или предмета. Например, нарисуйте прямоугольник (или используйте прямоугольник, который вы нарисовали в предыдущей главе). В приведенном примере для вычисления площади прямоугольника необходимо найти его длину и ширину.
- Для измерения длины и ширины прямоугольника воспользуйтесь линейкой или рулеткой. В приведенном примере воспользуемся значениями сторон прямоугольника из предыдущей главы, а именно ширина = 3 см, длина = 5 см.
2
Суть площади геометрической фигуры. Вычисление площади, ограниченной замкнутым контуром, подобно разбиению внутреннего пространства фигуры на квадраты размером 1 единица х 1 единица. Имейте в виду, что площадь фигуры может быть больше или меньше периметра этой фигуры.
- Вы можете разбить данную вам фигуру на единичные квадраты (1 см х 1 см или 1 м х 1 м), чтобы визуализировать процесс вычисления площади фигуры.
3
Перемножьте длину и ширину прямоугольника. В приведенном примере: площадь = 3 * 5 = 15 квадратных сантиметров. Помните, что площадь измеряется в квадратных единицах измерения (квадратные километры, квадратные метры, квадратные сантиметры и так далее).
- Вы можете записать единицы измерения площади в следующем виде:
  - километры²/км²
  - метры²/м²
  - сантиметры²/см²
4
К разным фигурам применяйте различные формулы. Для вычисления площади фигуры другой формы потребуется соответствующая формула. Вы можете воспользоваться следующими формулами для вычисления площади стандартных геометрических фигур:
- Параллелограмм: площадь = основание х высота
- Квадрат: площадь = сторона 1 х сторона 2
- Треугольник: площадь = ½ х основание х высота
  - В некоторых учебниках эта формула выглядит так: S = ½аh.
- Круг: площадь = π х радиус²
  - Радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя.^[12]^[13]
Реклама

Советы

Приведенные в этой статье формулы для вычисления площади и периметра применимы к двумерным фигурам. Если вам нужно найти объем трехмерной фигуры, например, конуса, куба, цилиндра, призмы или пирамиды, найдите соответствующую формулу в учебнике или в интернете.

Что вам понадобится

Бумага
Карандаш
Калькулятор (по желанию)
Рулетка (по желанию)
Линейка (по желанию)

Об этой статье

Эту страницу просматривали 237 067 раз.

Была ли эта статья полезной?

Источник

Формулы круга и окружности

Формула площади круга
Формула периметра круга (длины окружности)

Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое.

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью.

Формула площади круга

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади круга выражается числом заключающихся в него квадратных единиц.

1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).

2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

S — площадь круга

π — число пи (3.1415)

r — радиус круга

Формула периметра круга (длины окружности)

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

1) Периметр круга равен произведению радиуса на два пи (3.1415).

P — Периметр круга (длина окружности)

π — число пи (3.1415)

r — радиус круга (окружности)

Длина окружности

Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):

Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.

Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.

Задачи на длину окружности

Задача 1. Найти длину окружности, если её диаметр равен 5 см.

Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

C ≈ 3,14 · 5 = 15,7 (см).

Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:

теперь найдём длину окружности, умножив π на диаметр:

C ≈ 3,14 · 7 = 21,98 (м).

Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:

следовательно, радиус будет равен:

R	≈	7,85	=	7,85	= 1,25 (м).
2 · 3,14	6,28

Задачи на площадь круга

Задача 1. Найти площадь круга, если его радиус равен 2 см.

Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).

Ответ: 12,56 см 2 .

Задача 2. Найти площадь круга, если его диаметр равен 7 см.

Решение: Сначала найдём радиус круга, разделив его диаметр на 2:

теперь вычислим площадь круга по формуле:

S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).

Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

S = π	D 2	≈ 3,14 ·	7 2	= 3,14 ·	49	=
4	4	4

=	153,86	= 38,465 (см 2 ).
4

Ответ: 38,465 см 2 .

Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .

Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:

Что такое периметр и площадь

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a*4

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S= a*a

S=a 2

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Площадь всегда измеряется в квадратных единицах (см 2 , м 2 , мм 2 ). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

источники:

http://izamorfix.ru/matematika/planimetriya/dlina_okruj.html

http://topkin.ru/voprosy/nauka-voprosy/chto-takoe-perimetr-i-ploshhad/

Источник

Syntax

Steps

Example 1

Output

Example 2

Output

Периметр: формулы и методы вычисления длины контуров

Квадрат

Прямоугольник

Треугольник

Круг

Многоугольник

Заключение

1. Примерный план:

2. Описанный прямоугольник и описанный круг

Советы

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

Формулы круга и окружности

Формула площади круга

Формула периметра круга (длины окружности)

Длина окружности

Длина окружности

Задачи на длину окружности

Задачи на площадь круга

Что такое периметр и площадь

Как вычислить периметр

Периметр и площадь квадрата

Периметр и площадь прямоугольника

Периметр круга (длина окружности)

Отличие периметра от площади

Не пропустите также: