Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
Спрятать решение
Решение.
Введём обозначения, как показано на рисунке. Периметр верхнего левого прямоугольника равна 24, поэтому
аналогично,
При помощи полученной системы уравнений выразим значение
Из третьего уравнения получаем: следовательно, искомый периметр равен 12.
Ответ: 12.
Приведем ещё одно решение.
Нетрудно проверить, что суммы периметров расположенных на одной и другой диагоналях прямоугольника равны. Тогда: а потому неизвестный периметр равен 12.
Приведем ещё одно решение.
Несложно понять, что разность периметров двух верхних прямоугольников равна разности периметров двух нижних. Поэтому откуда вытекает, что неизвестный периметр равен 12.
Формулировка задачи: Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны A, B и C. Найдите периметр четвёртого прямоугольника.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
Пример задачи:

Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
Решение:
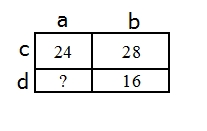
Для удобства дадим название каждой стороне прямоугольника (см. рисунок). И распишем, чему равен периметр каждого маленького прямоугольника по часовой стрелке:
P1 = 2a + 2c = 24
P2 = 2b + 2c = 28
P3 = 2b + 2d = 16
P4 = 2a + 2d = ?
Выразим стороны a и d из первого и третьего периметра и подставим их в периметр четвертого прямоугольника:
2a = 24 – 2c
2d = 16 – 2b
P4 = 24 – 2c + 16 – 2b
Мы также можем выразить сторону b через второй периметр, чтобы периметр четвертого прямоугольника был выражен только через одну сторону:
2b = 28 – 2c
P4 = 24 – 2c + 16 – (28 – 2c) = 24 – 2c + 16 – 28 + 2c = 24 + 16 – 28 = 12
В результате все неизвестные сократились и был найден периметр четверного прямоугольника, равный 12.
Ответ: 12
В общем виде решение данной задачи на смекалку выглядит следующим образом:
ПЕРИМЕТР ПРЯМОУГОЛЬНИКА = A + C – B
где A , B и C – периметры трех других прямоугольников, начиная с левого верхнего и далее по часовой стрелке.
Осталось лишь подставить все значения и получить ответ.
Обновлено: 14.11.2022
Задание
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.

Решение
При таком делении прямоугольника прямоугольными разрезами сумма периметров диагональных прямоугольников равны:
Р1+Р3=Р2+Р4
24+16=28+Р4
40=28+Р4
Р4=40-28
Р4=12
Ответ: 12
У задачу можно решать разными способами, в том числе и чисто логически:
периметр левого верхнего прямоугольника меньше периметра правого верхнего прямоугольника на 28 — 24 = 4 см, а значит, при одинаковой ширине этих прямоугольников, длина первого меньше длины второго прямоугольника на 4/2 = 2 см.
Нижние же прямоугольники отличаются от верхних тем, что их ширина меньше, при аналогичной длине, а значит длина нижнего левого прямоугольника меньше длины правого нижнего прямоугольника на те же 2 см, а значит периметр нижнего левого прямоугольника меньше периметра нижнего правого прямоугольника на 4 см и составляет 16 — 4 = 12 см.
Можно проверить немного по другому, периметр верхнего правого прямоугольника больше периметра нижнего правого прямоугольника на 28 — 16 = 12 см, а значит, чтобы найти периметр левого нижнего прямоугольника, нужно вычесть эти же 12 см из периметра верхнего левого прямоугольника: 24 — 12 = 12 см.
Математические можно решать так:
обозначим стороны малых прямоугольников, как на рисунке выше, a, b, c и d, соответственно.
Тогда периметр левого верхнего прямоугольника можно найти по формуле:
2( b + c ) = 24
периметр правого верхнего прямоугольника равен
2( b + d ) = 28
периметр правого нижнего прямоугольника равен
2( a + d ) = 16
Периметр же искомого прямоугольника можно вычислить, сложив периметры левого верхнего и правого нижнего прямоугольников и вычтя из полученной суммы периметр правого верхнего прямоугольника:
2( a + c ) = 2( b + c ) + 2( a + d ) — 2( b + d ) = 24 + 16 — 28 = 12 см.
В общем, ответ остаётся прежним: периметр четвёртого прямоугольника равен 12 см.
Прямоугольник двумя прямолинейными разрезами разбит на четыре малых прямоугольника (см. рис.). Периметры трех из них, начиная с левого верхнего и далее по часовой стрелке, равны (10), (14) и (20). Найдите периметр четвертого прямоугольника.
Решение
Обозначим равные стороны каждого прямоугольника (см. рисунок ниже). Периметр – сумма всех сторон, значит, периметр четвертого прямоугольника будет равен (P_4=a+d+a+d=2a+2d).
Распишем, чему равен периметр каждого маленького прямоугольника:
(P_1=2a+2c=10);
(P_2=2b+2c=14);
(P_3=2b+2d=20).
Выразим (a) из первого периметра, (d) из третьего периметра и подставим в четвертый периметр:
(2a=10-2c)
(2d=20-2b);
(P_4=10-2c+20-2b=30-2b-2c).
Выразим (b) из второго периметра и подставим в четвертый:
(2b=14-2c);
(P_4=30-(14-2c)-2c=16).
Таким, образом получили, что периметр четвертого прямоугольника равен (16).
Ответ: (16).
Источник: ЕГЭ 2019. Математика. Базовый уровень. Типовые тестовые задания. 14 вариантов заданий. (вариант №3) (Купить книгу)


