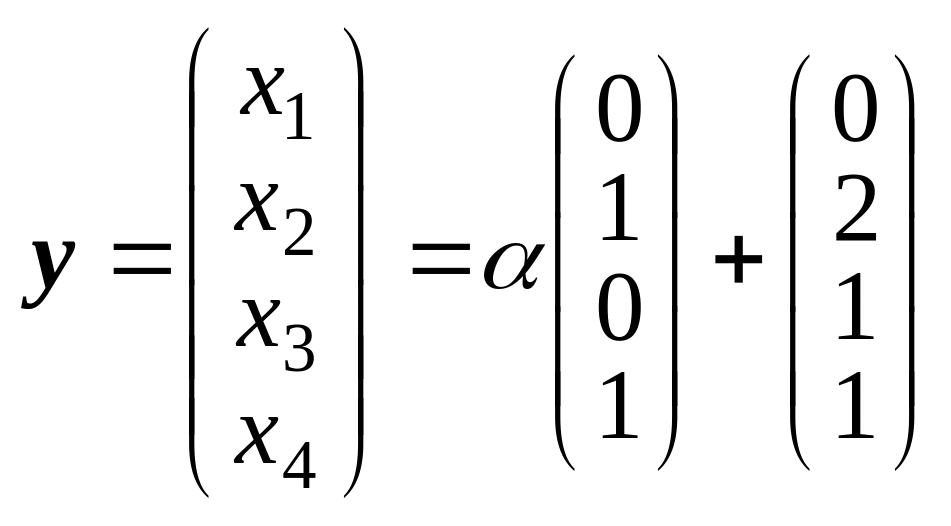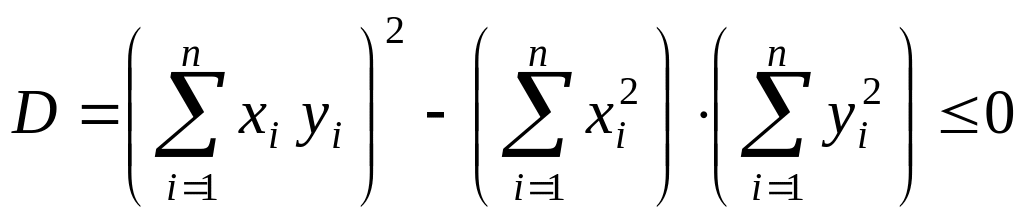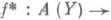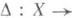|
Понятие
Способы
Свойства
Размерность Арифметические |
Понятие
линейного многообразия
При
рассмотрении примеров линейных
подпространств, было указано, что в
геометрическом пространстве
векторов пространства каждая прямая и
каждая плоскость, проходящие через
начало координат, определяют линейное
подпространство. Прямым и плоскостям,
не проходящим через начало координат,
соответствует в линейной алгебре новый
математический объект – линейное
многообразие.
Пусть
— линейное пространство,
— некоторое его подпространство,
содержащее векторы
,
(9)
—
некоторый вектор из пространства
.
Все векторы считаются отложенными от
начала координат. Множество
всевозможных векторов вида
,
где вектор
есть любой вектор из множества векторов
(9) или любая их линейная комбинация,
называется линейным
многообразием
и обозначается
.
Линейное многообразие, очевидно, получено
сдвигом подпространства
на вектор
(рис. 4.5). Вектор
называется вектором
сдвига,
подпространство
—
направляющим подпространством
линейного многообразия
.
Линейное
многообразие
обращается в линейное подпространство
,
когда вектор сдвига
.
Пусть
линейное подпространство
— это совокупность всех векторов, лежащих
на прямой, которая проходит через начало
координат (рис. 4.5). Положим один из этих
векторов равным
.
И пусть вектор
.
Тогда линейное многообразие
состоит из множества векторов
,
,
концы которых лежат на прямой, полученной
сдвигом исходной прямой на вектор
.
Способы
задания линейных многообразий
Линейное
многообразие может быть задано с помощью
векторов следующим образом: задается
базис векторного подпространства
и вектор сдвига
.
Другой
способ задания — посредством системы
неоднородных линейных уравнений.
Множество решений неоднородной системы
линейных уравнений является линейным
многообразием. Обоснуем это утверждение.
Напомним, что общее решение системы
линейных уравнений
складывается из общего решения
однородной системы
и базисного (частного) решения неоднородной
системы
.
Общее решение однородной системы есть
линейная комбинация фундаментального
набора решений (ФНР), задающего некоторое
линейное подпространство
.
Линейная комбинация ФНР плюс базисное
решение есть общее решение системы
неоднородных линейных уравнений. Поэтому
линейное многообразие можно представить
как множество решений некоторой в общем
случае неоднородной системы линейных
уравнений
.
Свойства
линейного многообразия.
-
Вектор
сдвигапринадлежит линейному многообразию.
◄Линейное
подпространство содержит нулевой
вектор:
.
Поэтому в суммах векторов
содержится вектор
.►
-
Вектором
сдвига, принадлежащим линейному
многообразию, может быть любой вектор
этого линейного многообразия.
◄Пусть
.
Возьмем произвольный вектор
.
Тогда существует вектор
такой, что
,
причем
.
Найдем сумму подпространства
и вектора
.
.
Получим
то же линейное многообразие
.►
-
Линейное
многообразиеопределяется однозначно
по известным подпространствуи вектору сдвига
.
◄Предположим,
что существует еще одно линейное
многообразие
,
построенное на линейном подпространстве
,
сдвинутом на вектор
.
Выберем базис
в подпространстве
.
Любой вектор
из линейного многообразия
может быть представлен в виде линейной
комбинации векторов базиса линейного
подпространства
и вектора сдвига
.
Точно
также, в виде линейной комбинации можно
представить любой вектор
из линейного многообразия
:
,
где
.
Но тогда вектор
,
а вектор
.
Векторы
и
— это произвольные векторы из линейных
многообразий
и
.
Следовательно,
=
.►
Размерность
линейного многообразия
Определение.
Размерностью
(рангом)
линейного многообразия
называется размерность линейного
подпространства
:
Если
линейное подпространство
состоит только из нулевого вектора, то
.
Такое линейное многообразие имеет
размерность
,
называется 0-мерным линейным многообразием
(ранг равен нулю) и геометрически
соответствует точке (конец единственного
вектора
).
Если
линейное подпространство
,
т.е.
состоит из векторов, лежащих на одной
прямой, то линейное многообразие
называется одномерным. Его ранг равен
единице. Геометрическая интерпретация
многообразия – прямая (концы всех
векторов лежат на прямой), не проходящая
через начало координат.
Линейное
многообразие, полученное из подпространства,
состоящего из векторов плоскости,
называется двумерным. Его геометрический
образ – плоскость.
В
–мерном векторном пространстве линейное
многообразие размерности
называется гиперплоскостью,
а размерности
,
где
,
— k-мерной
плоскостью.
Подобно
прямым или плоскостям линейные
многообразия могут пересекаться,
скрещиваться, быть параллельными.
Вводится также операция проектирования
одного линейного многообразия на другое.
Об этом подробнее в (9).
Операции
с линейными многообразиями и их взаимное
расположение.
-
Сумма
двух линейных многообразий
и
есть линейное многообразие,
определяемое по следующему правилу:
.
В
частном случае при
имеем
-
Пересечение
двух линейных многообразийи
есть линейное многообразие, вычисляемое
по правилу
,
где
.
-
Умножение
линейного многообразия
на число
порождает новое линейное многообразие
,
определяемое так:
.
-
Параллельность
двух линейных многообразийи
означает, что направляющее подпространство
одного из них содержит направляющее
подпространство другого:
,
если
или
.
-
Скрещивание
двух
линейных многообразийи
имеет место в том случае, если они не
пересекаются и не параллельны.
ПРИМЕР
1. Линейное многообразие
задано системой линейных уравнений
Найти
линейное подпространство
и вектор сдвига
такие, что
.
Решение.
Составим расширенную матрицу из
коэффициентов и свободных членов системы
уравнений и преобразуем ее, используя
метод Гаусса.
.
Вернемся
к системе уравнений, взяв свободными
переменными
.
Выделим фундаментальный
набор решений (ФНР)
.
Линейно
независимые векторы
составляют ФНР, а, следовательно, базис
подпространства
.
Любой вектор
можно представить в виде
.
Вектор сдвига есть вектор
.
ПРИМЕР
2. Линейное многообразие
имеет вид
,
где
,
,
,
.
Представить линейное
многообразие в виде системы линейных
уравнений.
Решение.
Линейное многообразие
есть множество векторов вида
или в координатном виде
.
Перепишем
систему уравнений относительно переменной
,
выделив столбец свободных членов.
.
Представим систему
матрицей коэффициентов и воспользуемся
методом Гаусса
.
Система совместна
при условии, что ранг матрицы коэффициентов
равен рангу расширенной матрицы (теорема
Кронекера-Капелли).
Следовательно,
или
Линейное
многообразие
записано в виде системы неоднородных
линейных уравнений.
Рассмотрим
вопросы взаимного расположения линейных
многообразий. Начнем с простого примера.
ПРИМЕР
3. Пусть в трехмерном линейном векторном
пространстве заданы два двухмерных
многообразия
где
и
,
где
Найти
пересечение линейных многообразий
.
Решение.
Произвольный вектор
,
принадлежащий
как одному так и другому линейному
многообразию, может быть представлен
в виде
(10)
или
,
где
– координаты вектора
в базисах направляющих подпространств
линейных многообразий. Для удобства
перепишем матричное уравнение так
Чтобы
найти
,
составим расширенную матрицу и
преобразуем ее методом Гаусса-Жордана
,
откуда
следует
.
Подставив
в равенство (10), получим
.
Следовательно,
две двухмерные плоскости пересекаются
по прямой (
).
Такой вывод можно сделать по виду
преобразованной методом Гаусса-Жордана
расширенной матрицы. Во второй строке
2-го и 3-го столбцов матрицы стоят отличные
от нуля цифры. Значит, существует только
одна независимая переменная, например,
.
ФНР содержит одно решение (один вектор).
Этот вектор составляет базис подпространства
размерности один, являющегося пересечением
направляющих подпространств линейных
многообразий.
Возможны
другие варианты решений для двух
плоскостей в трехмерном пространстве.
Пусть
преобразованная матрица имеет вид
.
Значок
поставлен в позициях, содержащих любое
число. Если на пересечении последних
столбца и строки стоит единица, решений
нет (линейные многообразия не пересекаются
).
Кроме того, поскольку
зависят от
,
ФНР будет содержать два независимых
решения (два вектора). Они составят базис
двухмерного подпространства. При наличии
единицы в последней строке последнего
столбца двухмерные плоскости параллельны.
Если
на пересечении последних столбца и
строки стоит нуль, решения существуют
(двухмерные плоскости пересекаются по
плоскости, т.е. совпадают,
.
Замечание.
В преобразованной методом Гаусса-Жордана
матрице в некоторых позициях могут
стоять вместо единиц и нулей другие
числа. Метод исследования взаиморасположения
многообразий остается справедливым,
если выполнены два условия:
-
Ранг
матрицы базиса направляющего
подпространства линейного многообразия
соответствует рангу матрицы, составленной
из столбцов, у которых только в одной
позиции по вертикали стоит единица. -
Если
все базисные векторы какого-либо
подпространства, расположенные по
столбцам, содержат нули в определенной
строке, то соответствующая матрица с
единицами только в одной позиции по
вертикали должна содержать в этой
строке нули.
ПРИМЕР
4. Рассмотреть все варианты взаимного
расположения трехмерного
и двумерного
многообразий в пятимерном пространстве.
Решение.
Перечислим существенно различные
варианты:
1)
,
2)
1а)
Комбинация цифр в последнем столбце
«
»
→
.
Многообразия не имеют общих точек.
1б)
Комбинация «
»
→
.
Многообразие
включено в многообразие
.
2а)
Цифра в последнем столбце «1»
→
.
Многообразия не имеют общих точек.
2б)
Цифра в последнем столбце «0»
→
Многообразия пересекаются по прямой.
3)
,
многообразия пересекаются в точке.
4.4.
Метрические пространства
|
Аксиомы
Нормы Геометрическая |
Аксиомы
метрического пространства
Векторное
пространство
называется
метрическим,
если задано некоторое правило, по
которому каждой паре векторов
ставится в соответствие некоторое число
.
Оно должно удовлетворять 3 аксиомам:
1.
для всех
и
при
.
2.
для всех
;
3.
для всех
.
Это
число
,
где
и
,
называется расстоянием
между векторами
или нормой,
а правило (функция двух векторов, формула)
– метрикой.
Метрику можно ввести по-разному. Докажем,
что векторное пространство
станет
метрическим, если для любых x
и y
из
положить
.
Покажем,
что выполняются аксиомы метрики.
Действительно, из свойств нормы вытекает,
что
-
,
причемтогда
и только тогда, когда
. -
. -
.
Нормы
метрического пространства
Модуль
разности векторов может быть вычислен
в координатах по-разному (разные нормы).
В экономике наиболее распространены
следующие:
-
евклидова
норма:
.
В
частном случае расстояние между вектором
и нулевым вектором
есть норма вектора
=
.
-
октаэдрическая
норма:
.
Норма
вектора в векторном пространстве с
октаэдрической нормой есть величина
=
.
-
кубическая
норма:
.
Норма
вектора
вычисляется по формуле
=
.
Задавая
по-разному модуль разности векторов в
координатах, мы должны убедиться в том,
что аксиомы метрики не нарушены. Проверим
справедливость аксиом на примере
евклидовой нормы.
-
Очевидно
,
причемпри
. -
3.
Аксиомадля метрики
имеет вид
.
Пусть
и
.
Тогда получим неравенство
,
которое
называется неравенством
треугольника.
Докажем его.
Запишем
неравенство в координатной форме
.
Для
доказательства возведем обе части в
квадрат и раскроем скобки. После упрощения
получим неравенство в координатах,
называемое неравенством
Коши-Буняковского
.
Докажем
его справедливость. Рассмотрим очевидное
неравенство
,
г
де
параметр
.
Раскрыв скобки, приведем его к квадратному
неравенству относительно
.
.
Поскольку
неравенство выполняется при всех
,
его дискриминант не положителен (
)
,
о
ткуда
получаем неравенство Коши-Буняковского.
Доказательство закончено.
Все
аксиомы проверены.
Геометрическая
интерпретация норм
Дадим
геометрическую интерпретацию каждой
нормы при
и
.
Для
евклидовой нормы величина
есть
расстояние между концами векторов
и
,
указанное пунктирной линией (рис. 4.6).
Эта величина соответствует расстоянию
между двумя точками на плоскости в нашем
физическом пространстве.
Октаэдрическая
норма устанавливает расстояние между
концами векторов
, (10)
п
оказанное
пунктирной линией на рис. 4.7. Наглядно
представить себе это расстояние можно
следующим образом. Представим себе, что
мы находимся в той части города, где
улицы пересекаются под прямыми углами
(рис. 4.8). Расстояние от А
до В
мы можем пройти, двигаясь по улицам, по
траектории АСВ
или, например, по траектории АDВ.
Но не можем пройти по траектории АВ.
Для нас расстояние от точки А
до точки В
вычисляется по формуле (10).
Расстояние,
определяемое кубической нормой
,
представлено
на рис. 4.9 пунктирной линией. Дадим
экономическую интерпретацию
этой нормы. Если вы можете заработать
ден. единиц, но обязаны израсходовать
ден. единиц, или, заработав
ден. единиц, израсходуете при этом
ден. единиц, ваш потребительский выбор,
нацеленный на наибольшую выгоду, будет
таким: максимум из двух величин
или
.
ПРИМЕР.
Метрика линейного векторного пространства
задается правилом
.
На координатной плоскости изобразить
множество точек, для которых
,
если в метрическом пространстве принята
1. евклидова норма; 2. октаэдрическая
норма; 3. кубическая норма. Ограничиться
рассмотрением случая
.
Решение.
В двумерном векторном пространстве
с евклидовой нормой и
уравнение
имеет вид
или
,
с октаэдрической нормой —
,
с кубической нормой —
.
На координатной плоскости
построим
соответствующие графики (рис. 4.10)
Д
ля
понимания того, как выглядит объемное
тело, если расстояния измерять, пользуясь
разными нормами, введем понятие
математического шара в метрическом
пространстве. Математическим
шаром
с центром в точке
и радиусом
в трехмерном метрическом пространстве
назовем множество
.
В
метрическом евклидовом пространстве
это неравенство имеет вид
и
представляет собой знакомый нам
геометрический шар. Евклидова норма
при
описывает наше физическое трехмерное
пространство.
В
линейном векторном пространстве с
октаэдрической нормой математический
шар
является
более сложной фигурой. Изобразим ее на
рис. 4.11, взяв центром точку
и радиусом
.
Это октаэдр (восьмигранник). Поэтому и
норма названа октаэдрической.
Математический
шар в линейном векторном пространстве
с кубической нормой
представляет
собой куб, отсюда название нормы.
Линейные многообразия: определение и примеры
Определение линейного многообразия
Пусть подпространство линейного пространства
, а
— некоторый вектор. Множество векторов
, представимых в виде
, где
, называется линейным многообразием, проходящим через вектор
параллельно подпространству
, и обозначается
(8.22)
Говорят также, что линейное многообразие получено параллельным сдвигом подпространства на вектор
, а подпространство
называют однородной частью линейного многообразия
. Размерностью линейного многообразия называют размерность его однородной части, т.е.
. B n-мерном линейном пространстве (n-l)-мерное линейное многообразие называется гиперплоскостью. Обратим внимание на то, что раз мерность многообразия равна максимальному числу линейно независимых векторов не самого многообразия, а его однородной части.
Примеры линейных многообразий
1. Любое подпространство является линейным многообразием
, где
— нулевой вектор.
2. В пространстве (радиус-векторов с общим началом в точке
) рассмотрим плоскость
, проходящую через точку
(рис.8.3) и плоскость
, проходящую через конец вектора
параллельно плоскости
.
Любой вектор , конец которого принадлежит плоскости
, можно пред ставить в виде
, где
— вектор, принадлежащий плоскости
. Следовательно, множество радиус-векторов, концы которых принадлежат плоскости
, это линейное многообразие
. Его размерность равна 2, так как
(базисом
являются любые два неколлинеарных вектора, принадлежащие
, например, векторы
и
). Заметим, что вектор
в многообразии
можно заменить любым радиус-вектором
, конец которого принадлежит плоскости
, т.е.
.
Свойства линейных многообразий
1. Линейное многообразие, параллельное линейному подпространству , однозначно определяется любым своим вектором, другими словами, если
, то
.
2. Непустое пересечение линейных многообразий является линейным многообразием, другими словами, если , то
, т.е. однородная часть пересечения совпадает с пересечением однородных частей многообразий, а вектор, определяющий сдвиг — это любой вектор пересечения многообразий.
3. Любое r-мерное линейное многообразие можно представить как аффинную оболочку не более, чем векторов.
В самом деле, пусть — r-мерное линейное многообразие, т.е.
. Выберем базис
подпространства
и образуем
векторов
линейного многообразия
. Покажем, что
. Действительно, любой вектор
можно представить в виде
. Преобразуем это выражение, подставляя
Получили аффинную комбинацию векторов , так как сумма коэффициентов равна единице. Следовательно,
.
Пусть теперь . Тогда
, причем
. Подставляя
, получаем:
то есть . Следовательно,
.
Из двух включений получаем равенство . Из доказательства следует, что
(8.23)
4. Аффинная оболочка непустого подмножества конечномерного пространства является линейным многообразием.
Взаимное расположение линейных многообразий
Линейные многообразия обобщают обычные объекты стереометрии -прямые и плоскости. Следующие признаки и определения обобщают известные стереометрические свойства, характеризующие взаимное расположение прямых и плоскостей. Геометрическая терминология естественно применяется для многообразий. Говорят, что одно линейное многообразие лежит в другом, если первое многообразие является подмножеством второго. Пересечение или объединение линейных многообразий понимается как пересечение или объединение множеств векторов. Говорят, что линейные многообразия не пересекаются, если у них нет общих векторов, т.е. пересечение этих множеств пусто.
Приведем признаки включения и равенства (совпадения) линейных многообразий:
1) линейное многообразие лежит в линейном многообразии
тогда и только тогда, когда
и
;
2) линейные многообразия и
совпадают тогда и толь ко тогда, когда
и
.
Два непересекающихся линейных многообразия и
называются параллельными, если одно из подпространств
или
лежит в другом:
или
(иными словами, если одна из однородных частей содержится в другой).
Два непересекающихся линейных многообразия и
называются скрещивающимися, если пересечение подпространств
и
есть нулевой вектор:
.
Способы описания линейных многообразий
Для линейных подпространств рассматривались два способа описания: внутренний (при помощи линейных оболочек) и внешний (при помощи однородной системы уравнений). Свойства 3, 4 определяют внутреннее описание линейных многообразий при помощи аффинных оболочек векторов. Внешнее описание линейных многообразий задается неоднородной системой линейных уравнений. Действительно, множество решений будем рассматривать как подмножество я -мерного арифметического пространства
. Структура общего решения неоднородной системы:
где — частное решение неоднородной системы,
— фундаментальная система решений соответствующей однородной системы
— произвольные постоянные,
— ранг матрицы системы. Как показано ранее, множество
решений однородной системы является линейным подпространством
, а именно
. Следовательно, множество
решений неоднородной системы является линейным многообразием в
(8.24)
В частности, множество решений одного уравнения с ненулевыми коэффициентами (хотя бы один коэффициент при неизвестных отличен от нуля), представляет собой гиперплоскость, т.е. линейное многообразие размерности
, так как размерность
его однородной части
равна
, поскольку
. Поэтому множество решений системы
линейных уравнений можно представить как пересечение
гиперплоскостей. По свойству 2 пересечение линейных многообразий есть линейное многообразие.
Равенство (8.24) определяет переход от внешнего описания линейного многообразия (левая часть) к внутреннему описанию (правая часть). Рас смотрим обратный переход: от внутреннего описания к внешнему.
Пусть дано линейное многообразие . Требуется составить неоднородную систему уравнений, множество решений которой совпадало бы с заданным многообразием. Учитывая, что разность двух решений неоднородной системы является решением однородной системы, используем переход от внутреннего описания линейного подпространства к внешнему. Для нахождения неоднородной системы нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу размеров
, а затем блочную матрицу
, приписав к матрице
единичную матрицу
n-го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу
к виду
, где
— простейший вид матрицы
.
3. Из последних строк матрицы
составить матрицу
.
4. Записать искомую систему уравнений в форме .
Пример 8.14. Многообразие задано аффинной оболочкой векторов
где
Составить систему неоднородных уравнений, задающую это же многообразие.
Решение. Согласно (8.23), зададим линейное многообразие в форме .
1. Из данных столбцов составляем матрицу , а затем блочную матрицу
2. Элементарными преобразованиями над строками блочной матрицы и над ее первыми тремя столбцами приводим левый блок к простейшему виду. Прибавляем ко второй и последней строке первую, умноженную на (-1), затем меняем местами вторую и третью строки:
Прибавим ко второму и третьему столбцам первый, умноженный на (-1), а затем к третьему столбцу — второй, умноженный на (-2). При этом в левом блоке получим простейший вид матрицы
(ее ранг
), а правый блок матрицы не изменится:
3. Из последних строк матрицы
составляем матрицу
4. Записываем искомую систему уравнений в форме
Пример 8.15. Найти размерность пересечения многообразий и
, если
— многообразие, заданное в примере 8.14 аффинной оболочкой век торов, а многообразие
— множество решений неоднородной системы
Решение. В примере 8.14 найдена система неоднородных уравнений, описывающая многообразие
Составляя из систем
и
одну систему, получаем внешнее описание пересечения многообразий:
. Найдем множество решений этой системы. Составляем матрицу системы и приводим ее к ступенчатому виду:
Система имеет единственное решение . Следовательно, пересечение многообразий состоит из одного вектора. Поскольку однороная часть пересечения представлена нулевым пространством, то
.
Пример 8.16. Исследовать взаимное расположение многообразий и
, если
— многообразие, заданное в примере 8.14 аффинной оболочкой векторов,
— многообразие, заданное в примере 8.15 неоднородной системой уравнений, а многообразие
— проходит через вектор
параллельно линейной оболочке вектора
.
Решение. В примере 8.15 показано, что многообразия и
пересекаются и
,
.
Найдем пересечения многообразия с многообразиями
и
. Любой вектор из
имеет вид
, где параметр
. Подставим выражения для координат этого вектора в системы, описывающие многообразия
и
(система для многообразия
получена в примере 8.14):
Каждая из систем несовместна. Следовательно, многообразие не пересекает многообразий
и
.
Найдем пересечение однородной части с однородными частями
и
. Однородная часть
задана линейной оболочкой
. Однородную часть
находим по правилу (8.23):
Так как , то справедливо включение
Поскольку однородная часть многообразия содержится в однородной части многообразия
, то, согласно определению, многообразия
и
параллельны.
Однородную часть определяем, используя структуру общего решения неоднородной системы (она была найдена при решении примера 5.5):
где — произвольные постоянные. По правилу (8.24)
. Найдем пересечение подпространств
и
. Для этого составляем матрицу
и приводим ее к ступенчатому виду
Поскольку , то размерность пересечения равна нулю:
. Так как
и многообразия
и
не пересекаются, то они скрещивающиеся.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание
Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.
Линейное пространство
Определения
Пусть дано множество $ mathbb V_{}=left{ X,Y,Z,U,dots right} $
элементов произвольной природы. Пусть для элементов этого множества определены
две операции: сложения $ X+Y_{} $ и умножения на любое вещественное число $ alpha_{} $:
$ alpha cdot X_{} $, и множество $ mathbb V_{} $ замкнуто относительно этих операций:
$ X+Y in mathbb V , alpha cdot X in mathbb V_{} $. Пусть эти операции подчиняются
аксиомам:
1.
$ X+Y=Y+X_{} $ для $ { X,, Y} subset mathbb V_{} $;
2.
$ (X+Y)+Z_{}=X+(Y+Z) $ для $ { X,, Y,, Z } subset mathbb V_{} $;
3.
в $ mathbb V_{} $ cуществует нулевой вектор $ mathbb O_{} $ со свойством $ X+ mathbb O =X_{} $ для $ forall Xin mathbb V_{} $;
4.
для каждого $ Xin mathbb V_{} $ существует обратный вектор $ X^{prime}in mathbb V_{} $ со свойством $ X+X^{prime}=mathbb O_{} $;
5.
$ 1cdot X=X_{} $ для $ forall Xin mathbb V_{} $;
6.
$ lambda left(mu X right)_{}= left(lambda mu right)X $ для $ forall Xin mathbb V_{} $, $ {lambda ,, mu } subset mathbb R_{} $ ;
7.
$ (lambda + mu)X=lambda X + mu X_{} $ для $ forall Xin mathbb V_{} $, $ {lambda ,, mu }subset mathbb R_{} $ ;
8.
$ lambda (X + Y) =lambda X_{} + lambda Y $ для $ { X,, Y} subset mathbb V_{} ,
lambda in mathbb R $.
Тогда такое множество $ mathbb V_{} $ называется линейным (векторным) пространством,
его элементы называются векторами, и — чтобы подчеркнуть их отличие от
чисел из $ mathbb R_{} $ — последние называются скалярами1).
Пространство, состоящее из одного только нулевого вектора, называется тривиальным .
Если в аксиомах
6
—
8
допустить умножение и на комплексные скаляры, то такое линейное пространство называется комплексным. Для упрощения рассуждений в настоящем разделе будут рассматриваться только вещественные пространства.
Линейное пространство является группой относительно операции сложения, причем группой абелевой.
Элементарно доказывается единственность нулевого вектора, и единственность
вектора, обратного вектору $ Xin mathbb V_{} $: $ X^{prime}=-1cdot X_{} $, его привычно обозначают $ — X_{} $.
Подмножество $ mathbb V_{1} $ линейного пространства $ mathbb V_{} $, само являющееся линейным
пространством (т.е. $ mathbb V_{1} $ замкнуто относительно сложения векторов и умножения на произвольный скаляр), называется линейным подпространством пространства $ mathbb V_{} $. Тривиальными подпространствами линейного пространства $ mathbb V_{} $
называются само $ mathbb V_{} $ и пространство, состоящее из одного нулевого вектора
$ mathbb O_{} $.
Примеры линейных пространств
П
Пример 1. Пространство $ mathbb R^{3} $ упорядоченных троек вещественных чисел $ (a_1,a_2,a_{3}) $ с операциями, определяемыми равенствами:
$$ (a_1,a_2,a_3)+(b_1,b_2,b_3)= (a_1+b_1,a_2+b_2,a_3+b_3),
alpha (a_1,a_2,a_3) = ( alpha a_1, alpha a_2, alpha a_3 ) .
$$
Геометрическая интерпретация очевидна: вектор в пространстве, «привязанный» к началу координат, может быть задан координатами своего конца $ (a_1,a_2,a_{3}) $. На рисунке показано и типичное подпространство пространства $ mathbb R^{3} $: плоскость, проходящая через начало координат.
Точнее говоря, элементами $ mathbb V_1 $ являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения2) очевидна.
Исходя из этой геометрической интерпретации, часто говорят о векторе $ X_{} $ произвольного линейного пространства $ mathbb V_{} $ как о точке пространства $ mathbb V_{} $. Иногда эту точку
называют «концом вектора $ X_{} $». Кроме удобства ассоциативного восприятия, этим словам не придается никакого формального смысла: понятие «конец вектора» отсутствует в аксиоматике линейного пространства.
П
Пример 2. Основываясь на том же примере, можно дать и иную интерпретацию векторного пространства $ mathbb V_1 $ (заложенную, кстати, уже в самом происхождении слова «вектор»3))
— оно определяет набор «сдвигов» точек пространства $ mathbb R^{3} $. Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости $ mathbb V_1 $.
Вообще говоря, с подобными интерпретациями понятия вектора все обстоит не так просто. Попытки аппелировать к его физическому смыслу — как к объекту, имеющему величину и направление — вызывают справедливую отповедь строгих математиков.
Определение же вектора как элемента векторного пространства очень напоминает эпизод с сепульками из знаменитого фантастического рассказа Станислава Лема (см.
☞
ЗДЕСЬ ). Не будем зацикливаться на формализме, а исследуем этот нечеткий объект в его частных проявлениях.
П
Пример 3. Естественным обобщением пространства $ mathbb R^{3} $ служит пространство $ mathbb R_{}^{n} $ —
векторное пространство строк $ (x_1,dots,x_{n}) $ или столбцов
$ (x_1,dots,x_n)^{^top} $. Один из способов задания подпространства
в $ mathbb R_{}^{n} $ — задание набора ограничений. Множество решений системы линейных однородных уравнений:
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&0,\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&0,\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&0
end{array}right.
iff
AX=mathbb O
$$
образует линейное подпространство пространства $ mathbb R_{}^{n} $. В самом деле, если
$$x_1=alpha_1,dots, x_n=alpha_n $$
— решение системы, то и
$$x_1=t alpha_1,dots, x_n= t alpha_n $$
— тоже решение при любом $ t in mathbb R $. Если
$$x_1=beta_1,dots, x_n=beta_n $$
— еще одно решение системы, то и
$$x_1=alpha_1+beta_1,dots,x_n=alpha_n+beta_n $$
— тоже будет ее решением.
?
Почему множество решений системы неоднородных уравнений не образует линейного подпространства?
П
Пример 4. Обобщая далее, можем рассмотреть пространство «бесконечных» строк или последовательностей
$$ (x_1,dots,x_n, dots ) , , $$
обычно являющееся объектом математического анализа — при рассмотрении последовательностей и рядов. Подпространство этого пространства образуют, например, линейные рекуррентные последовательности $ {x_k}_{k=0,1,2,dots } $ удовлетворяющие — при произвольных числах $ {x_0,dots x_{n-1} } subset mathbb R $ — линейному однородному разностному уравнению $ n_{} $-го порядка,
$$
x_{n+K}=a_1 x_{n+K-1}+ dots+ a_n x_K npu K in {0,1,2,dots } ;
$$
здесь числа $ { a_1,dots,a_{n-1}, a_n ne 0 } subset mathbb R $ считаются фиксированными.
Можно рассматривать строки (последовательности) «бесконечные в обе стороны» $ { dots,x_{-2},x_{-1},x_0,x_1,x_2,dots } $ — они используются в ТЕОРИИ СИГНАЛОВ.
П
Пример 5. Множество $ mtimes n_{} $-матриц с вещественными элементами с операциями сложения матриц и умножения на вещественные числа образует линейное пространство. Будем обозначать это пространство $ mathbb R^{mtimes n} $.
В пространстве квадратных матриц
фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство:
симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.
П
Пример 6. Множество полиномов одной переменной $ x_{} $ степени в точности равной $ n_{} $ с коэффициентами из $ mathbb A_{} $ (где $ mathbb A_{} $ — любое из множеств $ mathbb Z, mathbb Q, mathbb R_{} $ или $ mathbb C_{} $) с обычными операциями сложения полиномов и умножения на число из $ mathbb A_{} $
не образует линейного пространства. Почему? — Потому что оно не является замкнутым относительно сложения: сумма полиномов
$$ f(x)=x^n -x+1 quad mbox{ и } quad g(x)=-x^n+x^{n-1}-2 $$
не является полиномом $ n_{} $-й степени. Но вот множество полиномов степени
не выше $ n_{} $ $$ mathbb P_n= left{ p(x) in mathbb A [x] big| deg p(x) le n right} $$
линейное пространство образует; только к этому множеству надо придать еще и тождественно нулевой полином4). Очевидными подпространствами $ mathbb P_{n} $ являются $ mathbb P_{0}, mathbb P_1,dots,mathbb P_{n-1} $. Кроме того, подпространствами будут множество четных и множество нечетных полиномов степени не выше $ n_{} $. Множество всевозможных полиномов
$$
mathbb P= bigcup_{n=0}^{infty} mathbb P_n
$$
(без ограничения на степени) тоже образует линейное пространство.
П
Пример 7. Обобщением предыдущего случая будет пространство полиномов нескольких переменных $ x_1,dots, x_{ell} $ степени не выше $ n_{} $ с коэффициентами из $ mathbb A_{} $. Например, множество линейных полиномов
$$ left{ a_1x_1+dots+a_{ell}x_{ell}+b big| (a_1,dots,a_{ell},b) in mathbb A^{ell+1} right} $$
образует линейное пространство. Множество однородных полиномов (форм) степени $ n_{} $ (с присоединением к этому множеству тождественно нулевого полинома) — также линейное пространство.
С точки зрения приведенного в предыдущем пункте определения, множество строк с целочисленными компонентами
$$ mathbb Z^n = left{ (x_1,dots,x_n) mid {x_j}_{j=1}^n subset mathbb Z right} , $$
рассматриваемое относительно операций покомпонентного сложения и умножения на целочисленные скаляры, не является линейным пространством. Тем не менее, все аксиомы
1
—
8
будут выполнены если мы допустим умножение только на целочисленные скаляры. В настоящем разделе мы не будем акцентировать внимание на этом объекте, но он довольно полезен в дискретной математике, например в
☞
ТЕОРИИ КОДИРОВАНИЯ. Линейные пространства над конечными полями рассматриваются
☞
ЗДЕСЬ.
Изоморфизм
Пусть имеются два линейных пространства разной природы: $ mathbb V_{} $ с операцией $ +_{} $ и $ mathbb W_{} $
с операцией $ boxplus_{} $. Может оказаться так, что эти пространства «очень похожи», и свойства одного получаются простым «переводом» свойств другого.
Говорят, что пространства $ mathbb V_{} $ и $ mathbb W_{} $ изоморфны если между множествами их элементов можно установить такое взаимно-однозначное соответствие, что если $ X_{} leftrightarrow X^{prime} $ и $ Y_{} leftrightarrow Y^{prime} $ то $ X+Y leftrightarrow X_{}^{prime} boxplus Y^{prime} $ и
$ lambda X_{} leftrightarrow lambda X^{prime} $.
=>
При изоморфизме пространств $ mathbb V_{} $ и $ mathbb W_{} $ нулевому вектору одного пространства будет соответствовать нулевой вектор другого пространства.
П
Пример. Пространство $ mathbb R^{n}_{} $ изоморфно пространству $ mathbb P_{n-1}^{} $.
В самом деле, изоморфизм устанавливается соответствием
$$ [a_1,dots,a_n] leftrightarrow a_1+a_2x+dots + a_nx^{n-1} .$$
П
Пример. Пространство $ mathbb R^{mtimes n} $ вещественных матриц порядка $ m_{}times n $ изоморфно пространству
$ mathbb R_{}^{mn} $. Изоморфизм устанавливается с помощью операции векторизации матрицы
(матрица «вытягивается» в один столбец).
П
Пример. Пространство квадратичных форм от $ n_{} $ переменных изоморфно пространству симметричных матриц $ n_{} $-го порядка. Изоморфизм устанавливается соответствием, которое мы проиллюстрируем для случая $ n=3_{} $:
$$
a_{11}x_1^2+a_{12}x_1x_2+a_{13}x_1x_3+a_{22}x_2^2+a_{23}x_2x_3+a_{33}x_3^2 leftrightarrow
left(
begin{array}{ccc}
a_{11} & frac{1}{2}a_{12} & frac{1}{2}a_{13} \
frac{1}{2}a_{12} & a_{22} & frac{1}{2}a_{23} \
frac{1}{2}a_{13} & frac{1}{2}a_{23} & a_{33}
end{array}
right) .
$$
Понятие изоморфизма вводится для того, чтобы исследование объектов, возникающих в различных областях алгебры, но с «похожими» свойствами операций, вести на примере одного образца, отрабатывая на нем результаты, которые можно будет потом дешево тиражировать. Какое именно линейное пространство взять «за образец»? — См. концовку следующего пункта.
Линейная зависимость, базис, координаты
Линейной комбинацией системы векторов $ {X_1,dots,X_{m}} $ называется произвольный вектор
$$ alpha_1 X_1+dots+ alpha_m X_m $$
при каких-то фиксированных значениях скаляров $ alpha_{1}, dots, alpha_{m} $.
Множество всевозможных линейных комбинаций системы векторов $ {X_1,dots,X_{m}} $
$$
left{ alpha_1 X_1+dots+ alpha_m X_m bigg| {alpha_1,dots,alpha_m}subset mathbb R right}
$$
называется линейной оболочкой векторов $ X_1,dots,X_{m} $ и обозначается $ {mathcal L}(X_1,dots,X_{m}) $.
Т
Теорема 1. Линейная оболочка векторов $ X_1,dots,X_{m} $ образует линейное подпространство пространства $ mathbb V_{} $.
П
Пример. В пространстве $ mathbb P_{n} $ полиномов степеней $ le n_{} ge 3 $ линейной оболочкой полиномов $ x,x^2,x^3 $ будет множество полиномов вида
$ a_0x^3+a_1x^2+a_2x $, т.е. множество полиномов степеней $ le 3 $, имеющих корень $ lambda_{}=0 $.
♦
Система векторов $ { X_{1},dots,X_m } $
называется линейно зависимой (л.з.) если существуют числа $ alpha_{1},dots,alpha_m $, такие что хотя бы одно из них отлично от нуля и
$$
alpha_1X_1+dots+alpha_mX_m=mathbb O
$$
Если же это равенство возможно только при $ alpha_{1}=0,dots,alpha_m=0 $,
то система векторов называется линейно независимой (л.н.з.).
П
Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)
$$ f_1=(x_1+x_2+x_3)^2,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$
являются линейно зависимыми, поскольку
$$ f_1-2,f_2-f_3 equiv 0 . $$
Полиномы
$$ tilde f_1=x_1+x_2+x_3,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$
не являются линейно зависимыми, но являются функционально зависимыми, поскольку
$$ tilde f_1^2-2,f_2-f_3 equiv 0 . $$
♦
Т
Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.
б) Если система л.н.з., то и любая ее подсистема л.н.з.
в) При $ m>1 $ система $ {X_{1},dots,X_m} $ л.з. тогда и только тогда,
когда по меньшей мере один ее вектор линейно выражается через остальные,
т.е. существуют $ jin {1,dots,n } $ и константы $ gamma_{1},dots,gamma_{j-1},
gamma_{j+1},dots,gamma_{n} $ такие, что
$$ X_j=gamma_1X_1+dots+gamma_{j-1}X_{j-1}+ gamma_{j+1}X_{j+1}+dots + gamma_{m}X_{m} .$$
Т
Теорема 3. Если каждый из векторов системы $ { X_1,dots,X_{m} } $ линейно выражается через векторы другой системы $ { B_{1},dots,B_k } $ с меньшим числом векторов: $ k<m $, то система $ { X_{1},dots,X_m } $ будет л.з.
Доказательство аналогично приведенному
☞
ЗДЕСЬ.
Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.
Т
Теорема 4. Системы векторов
$$ { X_1,dots,X_{m} } quad mbox{ и } quad { Y_{1},dots,Y_k } $$
будут эквивалентными тогда и только тогда когда совпадают линейные оболочки этих систем:
$${mathcal L}(X_1,dots,X_m)={mathcal L}(Y_1,dots,Y_k) . $$
Т
Теорема 5. Если каждая из двух эквивалентных систем
$$ { X_1,dots,X_{m} } quad mbox{ и } quad { Y_{1},dots,Y_k } $$
является л.н.з., то эти системы состоят из одинакового числа векторов: $ m=k_{} $ .
Линейно независимая система векторов $ {X_{j}}subset mathbb V $ называется базисом этого пространства если каждый $ Xin mathbb V $
можно представить в виде линейной комбинации указанных векторов:
$$
X=sum_{j} alpha_j X_j .
$$
При этом не подразумевается конечность системы, т.е. суммирование может распространяться на бесконечное число слагаемых. Так, например, пространство бесконечных строк (или последовательностей) $ left[a_{1},a_2,dots, right] $ имеет бесконечный базис, состоящий из векторов
$$ [underbrace{0,dots,0,1}_j,0,dots , ] quad npu j in mathbb N . $$
В случае, когда базис пространства $ mathbb V_{} $ конечен,
пространство $ mathbb V_{} $ называется конечномерным, а число векторов
базиса тогда называется размерностью пространства $ mathbb V_{} $ и
обозначается5): $ dim mathbb V_{} $. Также полагают, что размерность тривиального пространства, состоящего из одного только нулевого вектора, равна нулю: $ dim {mathbb O_{} }= 0 $.
П
Пример. Линейное пространство $ mtimes n_{} $ матриц имеет размерность $ mn_{} $. Так, для случая $ m_{}=3 ,n=2 $ в качестве базиса можно выбрать следующий набор матриц
$$
left(
begin{array}{cc}
1 & 0 \
0 & 0 \
0 & 0
end{array}
right) ,
left(
begin{array}{cc}
0 & 1 \
0 & 0 \
0 & 0
end{array}
right) ,
left(
begin{array}{ccccc}
0 & 0 \
1 & 0 \
0 & 0 end{array}
right) ,
left(
begin{array}{cc}
0 & 0 \
0 & 1 \
0 & 0 end{array}
right) ,
left(
begin{array}{cc}
0 & 0 \
0 & 0 \
1 & 0
end{array}
right) ,
left(
begin{array}{cc}
0 & 0 \
0 & 0 \
0 & 1
end{array}
right) .
$$
♦
?
Найти размерности подпространства симметричных и подпространства кососимметричных матриц порядка $ n_{} $.
П
Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением

под умножением цвета на положительное число $ k_{} $ — увеличение в $ k_{} $ раз яркости цвета
A
Анимация
☞
ЗДЕСЬ (1500 K, gif)
под умножением на $ (-1) $ — взятие дополнительного цвета. При этом оказывается, что совокупность всех цветов выражается линейно через три цвета: красный, зеленый и синий, т.е. образует трехмерное линейное пространство. (Точнее, некоторое тело в трехмерном пространстве, поскольку яркости цветов ограничены верхним порогом раздражения.) Исследование этого трехмерного тела всех цветов является важным орудием цветоведения.
♦
Если $ dim mathbb V=d_{} $ и вектора $ X_1,dots,X_{d} $ являются базисными для $ mathbb V_{} $, то разложение вектора $ X in mathbb V_{} $ в сумму:
$$ X=alpha_1 X_1+dots+ alpha_d X_d .$$
называется разложением вектора $ X_{} $ по базису $ X_1,dots,X_{d} $; при этом числа $ alpha_1,dots, alpha_{d} $ называются координатами вектора $ X_{} $
в данном базисе.
Т
Теорема 6. Если $ dim mathbb V=d>0 $, то любая система из $ d_{} $ линейно независимых векторов пространства образует базис этого пространства.
Доказательство. Пусть $ {Y_1,dots,Y_d} $ — л.н.з. система. Рассмотрим произвольный
$ Xin mathbb V_{} $. Если система $ {X,Y_1,dots,Y_d} $ л.н.з., то
$ dim mathbb V ge d+1 $, что противоречит условию теоремы. Следовательно, система линейно
зависима: $ alpha_0X+alpha_1Y_1+dots+alpha_dY_d=mathbb O $ при каком-то из чисел
$ {alpha_j}_{j=0}^{d} $ не равном нулю. Если $ alpha_0=0 $, то $ alpha_1Y_1+dots+alpha_dY_d=mathbb O $
при каком-то ненулевом коэффициенте. Это означает, что система
$ {Y_1,dots,Y_d} $ линейно зависима, что противоречит предположению.
Следовательно $ alpha_0ne 0 $, но тогда вектор $ X_{} $ может быть представлен
в виде линейной комбинации векторов $ Y_1,dots,Y_d $:
$$X=- {alpha_1}/{alpha_0} Y_1-dots -{alpha_d}/{alpha_0}Y_d .$$
По определению, система $ {Y_1,dots,Y_d} $ является базисом $ mathbb V $.
♦
Т
Теорема 7. Любой вектор $ X in mathbb V_{} $ может быть разложен по фиксированному базису пространства единственным образом.
Очевидно, $ dim mathbb R^{n} = n $: строки из $ n_{} $ элементов
$$[1,0,0,dots,0], [0,1,0,dots,0], [0,0,1,dots,0], dots , [0,0,0,dots,1]
$$
образуют базис этого пространства.
Имеются два способа задания линейных подпространств в $ mathbb R^{n}_{} $. Пусть
$$ mathbb V_1 = {mathcal L}(A_1,dots,A_k) quad npu {A_1,dots,A_k }
subset mathbb R^n .$$
В разделе
☞
РАНГ установлено, что
$$ dim mathbb V_1 = operatorname{rank} { A_1,dots,A_k } = operatorname{rank} (A) ,$$
где $ A_{} $ — матрица, составленная из строк (столбцов) $ A_{1},dots,A_k $.
П
Пример. Найти базис подпространства
$$mathcal L left([1,2,1,1],, [-1,0,-1,0], , [-1,2,-1,1], , [0,1,0,1] right)
.$$
Решение. Ищем
$$
operatorname{rank}
left(
begin{array}{rrrr}
1 & 2 & 1 & 1 \
-1&0&-1&0 \
-1& 2 &-1 &1 \
0& 1& 0 & 1
end{array}
right)
$$
по методу окаймляющих миноров. Существует минор третьего порядка
$$
left|
begin{array}{rrrr}
1 & 2 & 1 \
-1&0&0 \
0& 1 & 1
end{array}
right|
$$
отличный от нуля, а определитель самой матрицы равен нулю. Замечаем,
что найденный отличный от нуля минор расположен в первой, второй и
четвертой строках матрицы. Именно эти строки и образуют базис.
Ответ. Базис составляют, например, первая, вторая и четвертая строки.
Другим способом задания линейного подпространства в $ mathbb R^{n} $ может служить
задание набора ограничений, которым должны удовлетворять векторы
подпространства. Таким набором ограничений может являться, например,
система уравнений
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&0,\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&0,\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&0
end{array}right. qquad iff qquad AX=mathbb O .
$$
Какова размерность подпространства решений этой системы?
На этот вопрос мы ответим сразу же,
если вспомним определение фундаментальной системы решений (ФСР).
Именно, ФСР — как набор линейно независимых
решений, через которые линейно выражается любое решение системы однородных уравнений — является базисом подпространства этих решений.
Т
Теорема 8. Множество решений системы однородных уравнений $ AX=mathbb O_{} $ образует линейное подпространство пространства $ mathbb R^{n} $. Размерность этого подпространства равна $ n-operatorname{rank} (A) $, а фундаментальная система решений образует его базис.
П
Пример. В пространстве $ mathbb P_{n} $ полиномов степеней $ le n_{} $ каноническим базисом можно взять систему мономов $ {1,x,x^2,dots, x^n } $, т.е. $ dim mathbb P_{n} =n+1 $. Координатами полинома
$$ f(x)=a_0+a_1x+a_2x^2+dots+a_nx^n $$ будут его коэффициенты. Можно выбрать и другой базис, например,
$ {1, x-c,(x-c)^2,dots,(x-c)^n } $ при произвольном числе $ c_{} $. Координатами полинома в этом базисе будут теперь коэффициенты формулы Тейлора:
$$
f(x) equiv f(c)+
frac{f^{prime}(c)}{1!} (x-c) + frac{f^{prime prime }(c)}{2!} (x-c)^2+
dots + frac{f^{(n)}(c)}{n!} (x-c)^{n} .
$$
?
Найти координаты полинома
$$ x^5-x^4+x^3-x^2-x+1 $$
в базисе $ {1,x+1,x^2+1,x^3+1,x^4+1,x^5+1} $.
Т
Теорема 9. Любое векторное пространство $ mathbb V_{} $ размерности $ d_{} $ изоморфно $ mathbb R^{d} $.
Доказательство. Изоморфизм можно установить следующим соответствием.
Если $ {X_1,dots , X_d } $ — какой-то базис $ mathbb V_{} $, то вектору
$ X in mathbb V $ поставим в соответствие набор его координат в этом базисе:
$$ X=x_1X_1+dots+x_d X_d Rightarrow
X mapsto [x_1,dots,x_d]in mathbb R^d .
$$
На основании теоремы $ 6 $, такое соответствие будет взаимно-однозначным,
а проверка двух свойств изоморфизма тривиальна.
♦
Последний результат позволяет свести исследование свойств произвольного линейного пространства $ mathbb V_{} $ к исследованию свойств пространства $ mathbb R^{d} $. Лишь бы только удалось нам найти базис пространства $ mathbb V_{} $, а также разложение произвольного вектора по этому базису.
Однако некоторые теоретические заключения можно сделать основываясь только лишь на фактах принципиального существования
базиса и возможности разложения по нему произвольного вектора.
Критерии линейной зависимости
Т
Теорема . Строки
$$
{(a_{11},dots,a_{1n}),dots, (a_{n1},dots,a_{nn})} subset mathbb C^n
$$
линейно зависимы тогда и только тогда, когда
$$
left|begin{array}{rrr}
a_{11}&dots & a_{1n} \
dots & & dots \
a_{n1}& dots & a_{nn}
end{array}
right|=0 , .
$$
Т
Теорема . Строки
$$
{(a_{11},dots,a_{1n}),dots, (a_{m1},dots,a_{mn})} subset mathbb C^n
$$
линейно зависимы тогда и только тогда, когда
$$
operatorname{rank} A <m , , npu A=left(begin{array}{rrr}
a_{11}&dots & a_{1n} \
dots & & dots \
a_{m1}& dots & a_{mn}
end{array}
right) , .
$$
=>
Строки
$$
{(a_{11},dots,a_{1n}),dots, (a_{m1},dots,a_{mn})} subset mathbb R^n
$$
линейно зависимы тогда и только тогда, когда
$$
det (A^{top} A) = 0 , .
$$
(Определитель в левой части можно интерпретировать как определитель Грама системы строк.)
Т
Теорема . Аналитические на интервале $ ]a,b[ $ функции $ u_1(x),dots,u_n(x) $ линейно зависимы на $ ]a,b[ $ тогда и только тогда, когда их вронскиан
$$
left|
begin{array}{llll}
u_1(x) & u_2(x) & dots & u_n(x) \
u_1^{prime}(x) & u_2^{prime}(x) & dots & u_n^{prime}(x) \
u_1^{prime prime}(x) & u_2^{prime prime}(x)&dots& u_n^{prime prime}(x)\
dots & & & dots \
u_1^{(n-1)}(x) &u_2^{(n-1)}(x) &dots & u_n^{(n-1)}(x)
end{array}
right|
$$
тождественно равен нулю на $ ]a,b[ $.
Относительный базис
В настоящем пункте $ mathbb V_1 $ обозначает линейное подпространство пространства $ mathbb V_{} $, отличное от тривиального; обозначаем $ d_1=dim mathbb V_1 $.
Т
Теорема. Произвольный базис подпространства $ mathbb V_1 $ можно дополнить до базиса пространства $ mathbb V_{} $.
Доказательство. Пусть $ {X_1,dots,X_{d_1} } $ — какой-то
базис $ mathbb V_1 $. В пространстве $ mathbb V_{} $ найдется вектор
$ X_{d_1+1} $ такой, что система $ {X_1,dots,X_{d_1}, X_{d_1+1 }} $ будет л.н.з. (В противном случае, $ dim mathbb V=d_1 $, что противоречит условию настоящего пункта.) Если
$ d_1+1=d = dim mathbb V $, то, на основании теоремы 5 предыдущего пункта, требуемый
базис построен. Если же $ d_1+1<d $, то в пространстве
$ mathbb V_{} $ найдется вектор
$ X_{d_1+2} $ такой, что система $ {X_1,dots,X_{d_1}, X_{d_1+1 },X_{d_1+2 } } $
будет л.н.з. И т.д. Процесс закончится за конечное число
шагов.
♦

Говорят, что система векторов $ {X_1,dots,X_k} $ линейно независима относительно подпространства $ mathbb V_1 $ пространства $ mathbb V_{} $ если
$${.}_{} mbox{ из условия } quad alpha_1X_1+dots+alpha_k X_k in mathbb V_1 quad mbox{ следует } quad
alpha_1=dots=alpha_k=0 .$$
Т
Теорема. Обозначим $ {Y_1,dots,Y_{d_1}} $ — произвольный базис $ mathbb V_1 $.
Система $ {X_{1},dots,X_k} $ л.н.з. относительно $ mathbb V_1 $ тогда и
только тогда, когда система $ {Y_1,dots,Y_{d_1},X_1,dots,X_k} $ линейно независима.
П
Пример. Найти все значения параметра $ {color{Red} alpha } $, при которых система
$${ X_1=[1,, 2,, {color{Red} alpha },, 1 ]^{^{top}}, X_2=[1,, {color{Red} alpha },, 2,, 1]^{^{top}} }
$$
л.н.з. относительно подпространства
$$mathbb V_1=left{X in mathbb R^4 bigg|
begin{array}{ll}
x_1+2,x_2-3,x_3+4, x_4 &=0, \
x_1+x_2-x_3 -x_4 &=0
end{array}
right} . $$
Решение. Базисом подпространства $ mathbb V_1 $ является произвольная
ФСР заданной системы однородных уравнений,
например $ {Y_1=[-1,2,1,0]^{^{top}}, Y_2=[6,-5,0,1]^{^{top}}} $. Теорема
утверждает, что система $ { X_1, X_2} $ л.н.з. относительно $ mathbb V_1 $
тогда и только тогда, когда система $ { X_1, X_2,Y_1,Y_2} $ л.н.з. (в обычном понимании). Последнее равносильно тому, что матрица, составленная
из этих векторов, должна иметь ранг равный $ 4_{} $.
$$operatorname{rank}
left(
begin{array}{rrrr}
1 & 1 &-1 & 6 \
2 & {color{Red} alpha } & 2 & -5 \
{color{Red} alpha } & 2 & 1 & 0 \
1 & 1 & 0 & 1
end{array}
right)=4 iff
left|
begin{array}{rrrr}
1 & 1 &-1 & 6 \
2 & {color{Red} alpha } & 2 & -5 \
{color{Red} alpha } & 2 & 1 & 0 \
1 & 1 & 0 & 1
end{array}
right|= {color{Red} alpha }^2-10, {color{Red} alpha } +16 ne 0 .
$$
Ответ. $ {color{Red} alpha }not in { 2,, 8} $.
Говорят, что система векторов $ {X_1,dots,X_k} $ образует базис пространства $ mathbb V_{} $ относительно (или над) $ mathbb V_1 $ если она л.н.з. относительно
$ mathbb V_1 $ и любой вектор $ Xin mathbb V_{} $ можно представить в виде
$$ X=c_1X_1+dots+c_kX_k+Y, quad mbox{ где } quad Yin mathbb V_1 . $$
Т
Теорема. Обозначим $ { Y_1,dots,Y_{d_1} } $ — произвольный базис подпространства $ mathbb V_1 $.
Система $ {X_1,dots,X_k} $ образует базис $ mathbb V_{} $ относительно $ mathbb V_1 $ тогда и
только тогда, когда система $ { X_1,dots,X_k,Y_1,dots,Y_{d_1} } $ образует
базис $ mathbb V_{} $.
Доказательство. Действительно, любой вектор $ Xin mathbb V_{} $ выражается через
векторы $ X_1,dots,X_k,Y_1,dots,Y_{d_1} $. По предыдущей теореме для линейной
независимости этих векторов необходимо и достаточно относительной линейной независимости
$ X_1,dots,X_k $.
♦
=>
Базис $ mathbb V_{} $ строится дополнением базиса $ mathbb V_1 $ векторами
$ X_1,dots,X_k $ линейно независимыми относительно $ mathbb V_1 $. Поэтому
$${.}_{} mbox{число векторов относительного базиса } = dim mathbb V — dim
mathbb V_1 .$$
Это число называется коразмерностью6) подпространства $ mathbb V_1 $ в пространстве $ mathbb V $.
Сумма и пересечение линейных подпространств
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства
линейного пространства $ mathbb V_{} $. Множество
$$ mathbb V_1+ mathbb V_2 = left{X_1+X_2 big| X_1 in mathbb V_1, X_2 in mathbb V_2 right}$$
называется суммой, а множество
$$ mathbb V_1 cap mathbb V_2 = left{X big| X in mathbb V_1, X in mathbb V_2 right}$$
— пересечением подпространств $ mathbb V_1 $ и $ mathbb V_2 $. Аналогично
определяется сумма и пересечение произвольного количества подпространств.
Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.
Как правило, $ mathbb V_1+ mathbb V_2 ne mathbb V _1 cup mathbb V_2 $.

Т
Теорема. $ mathbb V_1+ mathbb V_2 $ и $ mathbb V_1 cap mathbb V_2 $ являются
подпространствами линейного пространства $ mathbb V_{} $.
?
Докажите, что $ mathbb V_1+ mathbb V_2 $ — это подпространство минимальной размерности, содержащее как $ mathbb V_1 $, так и $ mathbb V_2 $.
Понятие суммы линейных подпространств является частным случаем суммы Минковского двух произвольных подмножеств $ mathbb A_1 $ и $ mathbb A_2 $ линейного пространства:
$$ mathbb A_1 + mathbb A_2 = { X+Y mid X in mathbb A_1, Y in mathbb A_2 } . $$
Для подмножеств $ mathbb A_1={ [1,0], [0,1], [0,-1] } $ и $ mathbb A_2={ [0,0], [1,1] } $ пространства $ mathbb R^2 $ имеем:
$$ mathbb A_1 + mathbb A_2 = { [1,0], [0,1], [0,-1], [2,1], [1,2] } , . $$
Т
Теорема. Имеет место формула:
$$
dim , mathbb V_1 + dim , mathbb V_2=dim , (mathbb V_1 cap mathbb V_2) +
dim , (mathbb V_1 + mathbb V_2) . $$
Доказательство
☞
ЗДЕСЬ.
?
Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог
формулы включений-исключений в следующем виде:
$$dim , mathbb V_1 + dim , mathbb V_2 + dim , mathbb V_3 —
$$
$$
-left{dim , (mathbb V_1 cap mathbb V_2) + dim , (mathbb V_1 cap mathbb V_3) +
dim , (mathbb V_2 cap mathbb V_3) right} + $$
$$+ dim , (mathbb V_1 cap mathbb V_2 cap mathbb V_3) =dim , (mathbb V_1 + mathbb V_2 + mathbb V_3) ?$$
Т
Теорема. Имеет место формула:
$${mathcal L}(X_1,dots,X_m)+{mathcal L}(Y_1,dots,Y_{ell})=
{mathcal L}(X_1,dots,X_m,Y_1,dots,Y_{ell}) ;
$$
здесь $ {mathcal L} $ означает линейную оболочку.
П
Пример. Найти базис суммы и размерность пересечения
$$mathbb V_1={mathcal L}left(
left[ begin{array}{r} 0 \1 \ 1 \ 1
end{array} right] ,
left[ begin{array}{r} 1 \1 \ 1 \ 2
end{array} right] ,
left[ begin{array}{r} -2 \0 \ 1 \ 1
end{array} right]
right)
quad mbox{ и } quad
mathbb V_2={mathcal L}left(
left[ begin{array}{r} -1 \3 \ 2 \ -1
end{array} right] ,
left[ begin{array}{r} 1 \1 \ 0 \ -1
end{array} right]
right)
$$
Решение. Действуя согласно предыдущей теореме, составляем матрицу из всех векторов
$$
left( begin{array}{rrrrr}
0 & 1 & -2 & -1 & 1 \
1 & 1 & 0 & 3 & 1 \
1 & 1 & 1 & 2 & 0 \
1 & 2 & 1 & -1 & -1
end{array}
right)
$$
и ищем ее ранг методом окаймляющих миноров. Имеем: $ operatorname{rank} = 3 $ при ненулевом миноре матрицы расположенном в первых трех ее столбцах.
Ответ. Базис $ mathbb V_1 + mathbb V_2 $ составляют векторы $ X_1,X_2,X_3 $;
$ dim , (mathbb V_1 cap mathbb V_2) = 3+2 — 3 =2 $.
Алгоритм нахождения базиса
$ {mathcal L}(X_1,dots,X_m) cap {mathcal L}(Y_1,dots,Y_{ell}) $
проиллюстрируем на примере.
П
Пример. Найти базис $ mathbb V_1 cap mathbb V_2 $ при
$$
begin{array}{l}
mathbb V_1={mathcal L} left(
left[
begin{array}{r}
1 \ -1 \ 1 \ -1 \ 1
end{array}
right],,
left[
begin{array}{r}
1 \ 2 \ 1 \ 2 \ 1
end{array}
right],,
left[
begin{array}{r}
0 \ 1 \ 0 \ 1 \ 0
end{array}
right]
right) \
{}_{} qquad qquad quad X_1 quad quad X_2 quad quad X_3
end{array}
,
begin{array}{l}
mathbb V_2={mathcal L} left(
left[
begin{array}{r}
1 \ 0 \ 0 \ 0 \ 1
end{array}
right],,
left[
begin{array}{r}
1 \ 1 \ 0 \ 1 \ 1
end{array}
right],,
left[
begin{array}{r}
0 \ 1 \ 1 \ 1 \ 0
end{array}
right]
right) \
{}_{} quad qquad qquad Y_1 qquad Y_2 quad quad Y_3
end{array}
.
$$
Решение.
1.
Сначала найдем базисы каждого из подпространств:
$$dim mathbb V_1=2, mathbb V_1=mathcal L(X_1, X_2) ; dim mathbb V_2=3,
mathbb V_2=mathcal L(Y_1, Y_2, Y_3) . $$
2.
Произвольный вектор $ Zin mathbb R^5 $, принадлежащий
$ mathbb V_1 cap mathbb V_2 $, должен
раскладываться по базису каждого из подпространств:
$$Z=alpha_1 X_1 + alpha_2 X_2= beta_1 Y_1 + beta_2 Y_2 + beta_3 Y_3 .$$
Для определения неизвестных значений координат составляем систему уравнений
$$
begin{array}{l}
qquad X_1 X_2 \
qquad {color{RubineRed} downarrow} {color{RubineRed} downarrow} \
left( begin{array}{rrrrrrr}
1 & 1 & -1 & &-1 & & 0 \
-1 & 2 & 0 & & -1 & & -1 \
1 & 1 & 0 & & 0 & & -1 \
-1 & 2 & 0 & & -1 & & -1 \
1 & 1 & -1 & & -1 & & 0
end{array}
right) \
qquad qquad qquad {color{RubineRed} uparrow} qquad {color{RubineRed} uparrow} qquad quad {color{RubineRed} uparrow} \
quad qquad qquad -Y_1 quad — Y_2 quad -Y_3
end{array}
left(
begin{array}{r}
alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3
end{array}
right)= mathbb O_{5times 1}
$$
и решаем ее по методу Гаусса с нахождением фундаментальной системы решений:
$$
left( begin{array}{rrrrr}
1 & 1 & -1 & -1 & 0 \
0 & 3 & -1 & -2 & -1 \
0 & 0 & 1 & 1 & -1 \
0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0
end{array}
right) left(
begin{array}{r}
alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3
end{array}
right)= mathbb O quad Rightarrow qquad mbox{ ФСР } qquad
begin{array}{rrr|rr}
alpha_1 & alpha_2 & beta_1 & beta_2 & beta_3 \ hline
-1/3 & 1/3 & -1 & 1 & 0 \
1/3 & 2/3 & 1 & 0 & 1
end{array}
$$
3.
Получившиеся значения координат позволяют выразить
базис пересечения — либо через базис подпространства $ mathbb V_1 $
(если использовать полученные значения для $ alpha_1,alpha_2 $), либо
через базис подпространства $ mathbb V_2 $
(если использовать $ beta_1,beta_2, beta_3 $). Например,
$$
Z_1=-1/3 X_1 + 1/3 X_2 = [0,1,0,1,0]^{^{top}},
$$
$$
Z_2=1/3 X_1 + 2/3 X_2 = [1,1,1,1,1]^{^{top}}
.
$$
Ответ.7) $ left{[0,1,0,1,0]^{^{top}},, [1,1,1,1,1]^{^{top}} right} $.
?
Найти базисы суммы и пересечения подпространств
$$
mathbb V_1=left{
Xin mathbb R^4 left|
begin{array}{rrrrl}
2,x_1&+x_2&+4,x_3&+x_4 &= 0, \
2,x_1&+x_2&+3,x_3& &=0
end{array}
right.
right}
$$
и
$$
mathbb V_2=
left{
Xin mathbb R^4 left|
begin{array}{rrrrl}
3,x_1&+2,x_2&-x_3&-6, x_4 &= 0, \
2,x_1&&+8,x_3 &+7, x_4 &=0
end{array}
right.
right} .
$$
Решение
☞
ЗДЕСЬ.
Прямая сумма линейных подпространств
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства линейного пространства $ mathbb V_{} $.
Говорят, что $ mathbb V_{} $ раскладывается в прямую сумму подпространств
$ mathbb V_1 $ и $ mathbb V_2 $ если любой вектор $ Xin mathbb V_{} $ может быть представлен
в виде $ X=X_1+X_2 $, где $ X_1in mathbb V_1,X_2in mathbb V_2 $ и
такое представление единственно. Этот факт записывают: $ mathbb V= mathbb V_1 oplus mathbb V_2 $. Вектор $ X_{1} $ называется проекцией вектора $ X_{} $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_{2} $.

П
Пример. Линейное пространство квадратных матриц порядка $ n_{} $
раскладывается в прямую сумму подпространств: подпространства симметричных
матриц и подпространства кососимметричных матриц. В самом деле, для матрицы
$ A_{ntimes n} $ справедливо разложение
$$A=frac{1}{2} left(A+A^{^top} right) + frac{1}{2} left(A-A^{^top} right)
$$
и в правой части первая скобка дает симметричную матрицу, а
вторая — кососимметричную. Покажите, что не существует иного
разложения матрицы $ A_{} $ в сумму симметричной и кососимметричной.
Т
Теорема. Пусть $ mathbb V=mathbb V_1 + mathbb V_2 $.
Эта сумма будет прямой тогда и только тогда, когда подпространства $ mathbb V_1 $ и $ mathbb V_2 $ имеют тривиальное пересечение:
$$mathbb V_1 cap mathbb V_2={mathbb O } .$$
Доказательство. Необходимость. Пусть сумма $ mathbb V_1 + mathbb V_2 $ — прямая, но существует вектор $ Xne mathbb O $, принадлежащий $ mathbb V_1 cap mathbb V_2 $.
Но тогда и вектор $ (-X) $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Для нулевого вектора $ mathbb O $ получаем два представления в виде суммы проекций на подпространства:
$$ mathbb O = mathbb O + mathbb O = X+ (-X) , . $$
Это противоречит понятию прямой суммы.
Достаточность. Если $ mathbb V_1 cap mathbb V_2={mathbb O } $, но существует вектор $ X in mathbb V_1 + mathbb V_2 $, имеющий два различных разложения в сумму проекций
$$ X=X_1+X_2 =Y_1+ Y_2 quad npu quad {X_1,Y_1} subset mathbb V_1, {X_2,Y_2} subset mathbb V_2, $$
то
$$ (X_1-Y_1)+(X_2-Y_2) =mathbb O quad Rightarrow quad X_1-Y_1=Y_2-X_2 , , $$
т.е. вектор $ X_1-Y_1 $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Но, по предположению, $ mathbb V_1 cap mathbb V_2={mathbb O } $, следовательно, $ X_1-Y_1=mathbb O $, но тогда и $ Y_2-X_2=mathbb O $.
♦
=>
Сумма $ mathbb V=mathbb V_1 + mathbb V_2 $ будет прямой тогда и только тогда, когда
базис $ mathbb V_{} $ может быть получен объединением базисов $ mathbb V_{j} $.
Сформулированное таким образом утверждение содержится во многих учебниках по линейной алгебре. Тем не менее, с формальной точки зрения, оно неверно. В самом деле,
пусть $ mathbb V_1 = {mathcal L}(X_1,X_2),, mathbb V_2 = {mathcal L}(X_2,X_3) $ при
линейно независимых $ X_1,X_2,X_3 $. Очевидно базис
$ mathbb V_1 + mathbb V_2 ={mathcal L}(X_1,X_2,X_3) $ получается объединением базисов
$ mathbb V_1 $ и $ mathbb V_2 $. В то же время $ mathbb V_1 cap mathbb V_2ne {mathbb O } $.
Причина возникновения этой ошибки кроется в содержании термина
«объединение базисов». С точки зрения терминологии теории множеств,
во множестве не могут содержаться одинаковые элементы (во множестве
они неразличимы). Однако мы с самого начала изложения допустили,
что в систему векторов могут входить одинаковые, которые различаются
порядком своего расположения (хотя это особо и не подчеркивалось, векторы
в системе всегда пронумерованы). Исходя из этих соображений, объединение
базисов $ mathbb V_1 $ и $ mathbb V_2 $ будет пониматься 
в настоящем пункте (и кое-где далее) как система векторов, в которую входят последовательно векторы базисов
$ mathbb V_1 $ и $ mathbb V_2 $ — с допуском дублей. В рамках такой договоренности,
для приведенного примера получим: объединение базисов линейных подпространств
$ {mathcal L}(X_1,X_2) $ и $ {mathcal L}(X_2,X_3) $ представляет систему
$ {X_1,X_2,X_2,X_3} $, которая, очевидно, не является базисом. Таким образом
сумма $ {mathcal L}(X_1,X_2)+{mathcal L}(X_2,X_3) $ не является прямой, и результат
следствия остается справедливым.
П
Пример [2]. Доказать, что сумма подпространств
$$mathbb V_1={mathcal L}left(
left[ begin{array}{r} 2 \3 \ 11 \ 5
end{array} right] ,
left[ begin{array}{r} 1 \1 \ 5 \ 2
end{array} right] ,
left[ begin{array}{r} 0 \1 \ 1 \ 1
end{array} right]
right)
quad mbox{ и } quad
mathbb V_2={mathcal L}left(
left[ begin{array}{r} 2 \1 \ 3 \ 2
end{array} right] ,
left[ begin{array}{r} 1 \1 \ 3 \ 4
end{array} right] ,
left[ begin{array}{r} 5 \2 \ 6 \ 2
end{array} right]
right)
$$
будет прямой и найти проекции вектора $ Z=[2,0,0,3]^{top} $ на эти подпространства.
Решение. Базисы $ mathbb V_1 $ и $ mathbb V_2 $ составляют соответственно системы
$ {X_2,X_3} $ и $ { Y_1,Y_2 } $, т.е. $ dim , mathbb V_1=dim , mathbb V_2 =2 $.
На основании следствия достаточно установить, что объединенная
система $ {X_2,X_3,Y_1,Y_2 } $ л.н.з. Для этого достаточно проверить, что определитель матрицы
$$
A=left(
begin{array}{rrrr}
1 & 0 & 2 & 1 \
1 & 1 & 1 & 1 \
5 & 1 & 3 & 3 \
2 & 1 & 2 & 4
end{array}
right)
$$
отличен от нуля. Поскольку это условие выполнено, то сумма $ mathbb V_1 + mathbb V_2 $ —
прямая и базис этой суммы состоит из взятых векторов.
Для нахождения разложения вектора $ X_{} $ по этому базису
решаем систему уравнений
$$A left[
begin{array}{c}
alpha_2 \ alpha_3 \ beta_1 \ beta_2
end{array}
right] = Z
$$
и получаем единственное решение:
$ alpha_2=-1,, alpha_3=-1,, beta_1 =1, , beta_2=1 $. Разложение
$ Z=Z_1+Z_2 $ составляют векторы $ Z_1=alpha_2 X_2+alpha_3 X_3 $ и
$ Z_2=beta_1 Y_1+beta_2 Y_2 $.
Ответ. $ Z=[-1,-2,-6,-3]^{top} + [3,2,6,6]^{top} $.
Линейные многообразия
Пусть $ mathbb V_1 $ — линейное подпространство пространства
$ mathbb V_{} $, а $ X_{0} $ — произвольный фиксированный вектор из $ mathbb V_{} $. Множество
$$ mathbb M = X_0+ mathbb V_1 = left{X_0+Y big| Y in mathbb V_1 right} $$
называется линейным многообразием (порожденным подпространством $ mathbb V_1 $). Размерностью этого
многообразия называется размерность порождающего его подпространства: $ dim mathbb M = dim mathbb V_1 $. В случае $ 1 < dim mathbb M = k < dim mathbb V $ о многообразии $ mathbb M $ говорят как о k-мерной плоскости (или гиперплоскости), а при $ k=1 $ — как о прямой.
Образно говоря, многообразие — это сдвиг порождающего его линейного подпространства.
П
Пример. Множество полиномов вида
$$ f(x)= a_0x^3+a_1x^2+a_2x+1 in mathbb R[x] , , $$
т.е. таких, что $ deg f le 3, f(0)=1 $ образует линейное многообразие, порожденное линейным подпространством полиномов $ { x(a_0x^2+a_1x+a_2) mid (a_0,a_1,a_2) in mathbb R^3 } $.
Пересечение многообразий определяется традиционным способом, а сумма многообразий не определяется. Будем называть многообразия, порожденные одним и тем же подпространством
$$ mathbb M = X_0+ mathbb V_1 quad u quad widetilde{mathbb M} = widetilde X_0+ mathbb V_1 , $$
параллельными многообразиями.
П
Пример. Множество столбцов пространства $ mathbb R^{n} $, удовлетворяющих системе уравнений
$$
left{begin{array}{ccc}
a_{11}x_1 +a_{12}x_2+ldots+a_{1n}x_n &=&b_1,\
a_{21}x_1 +a_{22}x_2+ldots+a_{2n}x_n &=&b_2,\
ldots& & ldots \
a_{m1}x_1 +a_{m2}x_2+ldots+a_{mn}x_n &=&b_m
end{array}right.
iff
AX={mathcal B} ,
$$
образует линейное многообразие.
При $ {mathcal B}ne mathbb O_{mtimes 1} $ это многообразие не будет являться линейным пространством. Структуру этого множества описывала теорема из пункта
☞
ОБЩЕЕ РЕШЕНИЕ: если система совместна, то ее
общее решение можно представить как сумму какого-то одного ее решения и общего
решения соответствующей однородной системы $ AX= mathbb O $. Таким образом, многообразие решений неоднородной системы $ AX={mathcal B} $ допускает «параметрическое представление»:
$$mathbb M=X_0+ {mathcal L}(X_1,dots,X_{n-{mathfrak r}})=
$$
$$=left{X_0+t_1
X_1+dots+ t_{n-{mathfrak r}} X_{n-{mathfrak r}} mid (t_1,dots, t_{n-{mathfrak r}}) in mathbb R^{n-{mathfrak r}} right} ; $$
здесь $ X_{0} $ означает частное решение системы (т.е. $ AX_0={mathcal B} $),
$ {X_1,dots,X_{n-{mathfrak r}}} $ — ФСР для системы $ AX= mathbb O $,
а $ mathfrak r= operatorname{rank} A= operatorname{rank} [Amid mathcal B] $.
Получаем, следовательно, $ (n-{mathfrak r}) $-мерную плоскость в $ mathbb R^n $, a в случае $ (n-{mathfrak r})=1 $ — прямую
$$mathbb M=X_0+tX_1 quad npu t in mathbb R ; $$
в последнем случае вектор $ X_{1} $ называют направляющим вектором этой прямой.
§
Некоторые задачи на линейные многообразия
☞
ЗДЕСЬ.
Факторпространство
определяется
☞
ЗДЕСЬ.
Преобразование координат при замене базиса
Пусть $ mathbb V_{} $ — линейное пространство размерности $ n_{} $, пусть
$$ {X_1,dots,X_n} quad u quad {{mathfrak X}_1,dots,{mathfrak X}_n}$$
— два произвольных его базиса («старый» и «новый»).
Задача. Вывести соотношения, связывающие координаты произвольного
вектора $ Xin mathbb V_{} $ в старом и новом базисах:
$$X=x_1X_1+dots+x_nX_n={mathfrak x}_1{mathfrak X}_1+dots+{mathfrak x}_n{mathfrak X}_n
.$$
Предположим, что нам известны координаты векторов нового базиса в старом:
$$
left{
begin{array}{ccc}
{mathfrak X}_1&=&c_{11}X_1+c_{21}X_2+dots+c_{n1}X_n, \
{mathfrak X}_2&=&c_{12}X_1+c_{22}X_2+dots+c_{n2}X_n, \
dots& & dots \
{mathfrak X}_n&=&c_{1n}X_1+c_{2n}X_2+dots+c_{nn}X_n.
end{array}
right.
$$
Матрица
$$
C=left(
begin{array}{cccc}
c_{11} & c_{12} & dots & c_{1n} \
c_{21} & c_{22} & dots & c_{2n} \
dots & & & dots \
c_{n1} & c_{n2} & dots & c_{nn} \
end{array}
right),
$$
по столбцам которой стоят координаты новых базисных векторов в старом базисе называется матрицей перехода от старого базиса к новому, а также — ввиду одного из приведенных ниже результатов — матрицей преобразования координат.
Т
Теорема. Матрица $ C_{} $ неособенная.
Доказательство. Cначала покажем справедливость утверждения в частном случае $ mathbb V=mathbb R^n $. Вектора нового и старого базисов являются столбцами из $ n $ вещественных чисел, и равенства, задающие элементы матрицы $ C_{} $, можно переписать в матричном виде:
$$
left[{mathfrak X}_1|dots|{mathfrak X}_nright]=left[X_1|dots|X_nright]cdot C .
$$
Здесь $ | $ означает конкатенацию. Поскольку системы $ {X_1,dots,X_n} $ и $ {{mathfrak X}_1,dots,{mathfrak X}_n} $ — базисные, то
$$det left[X_1|dots |X_nright] ne 0, quad
det left[{mathfrak X}_1|dots |{mathfrak X}_nright] ne 0 .$$
Из последнего матричного равенства (и теоремы Бине-Коши ) тогда следует, что $ det Cne 0 $.
Теперь докажем теорему для случая произвольного пространства. Если $ det C= 0 $, то столбцы матрицы $ C_{} $ линейно зависимы (см.
☞
ЗДЕСЬ ), т.е. существует линейная комбинация
$$alpha_1 c_{j1}+ dots+alpha_n c_{jn}=0 quad npu quad forall jin {1,dots,n } $$
и при некотором $ alpha_kne 0 $. Но тогда из формул
$$
left{
begin{array}{ccc}
{mathfrak X}_1&=&c_{11}X_1+c_{21}X_2+dots+c_{n1}X_n, \
{mathfrak X}_2&=&c_{12}X_1+c_{22}X_2+dots+c_{n2}X_n, \
dots& & dots \
{mathfrak X}_n&=&c_{1n}X_1+c_{2n}X_2+dots+c_{nn}X_n.
end{array}
right.
$$
следует, что
$$alpha_1 {mathfrak X}_1+ dots+alpha_n {mathfrak X}_n=mathbb O ,$$
что противоречит линейной независимости системы $ {{mathfrak X}_1,dots,{mathfrak X}_n} $.
♦
П
Пример. Найти матрицу перехода
| от базиса | к базису | |
|---|---|---|
| $ left[1,1,0,0,0right] $ | $ left[1,1,1,1,1right] $ | |
| $ left[1,0,1,0,0right] $ | $ left[1,1,1,1,0right] $ | |
| $ left[1,0,0,1,0right] $ | $ left[1,1,1,0,0right] $ | |
| $ left[1,0,0,0,1right] $ | $ left[1,1,0,0,0right] $ | |
| $ left[1,1,1,1,1right] $ | $ left[1,0,0,0,0right] $ |
Решение. Можно попытаться найти элементы матрицы $ C_{} $ напрямую — устанавливая формулы связи между строками. В нашем конкретном примере это не очень трудно сделать — первый и четвертый
столбцы матрицы $ C_{} $ вообще очевидны поскольку $ {mathfrak X}_1 = X_5,, {mathfrak X}_4 = X_1 $. Но мы пойдем по формальному пути и воспользуемся определяющим матричным соотношением, которое мы получили при доказательстве предыдущей теоремы. Поставим координаты базисных векторов по столбцам соответствующих матриц:
$$
left[{mathfrak X}_1|dots|{mathfrak X}_nright]=left[X_1|dots|X_nright]cdot C quad Rightarrow
$$
$$
Rightarrow C= left[X_1|dots|X_nright]^{-1} cdot left[{mathfrak X}_1|dots|{mathfrak X}_nright] .
$$
В нашем примере имеем:
$$
C=
left(
begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \
1 & 0 & 0 & 0 & 1 \
0 & 1 & 0 & 0 & 1 \
0 & 0 & 1 & 0 & 1 \
0 & 0 & 0 & 1 & 1
end{array}
right)^{-1}
left(
begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \
1 & 1 & 1 & 1 & 0 \
1 & 1 & 1 & 0 & 0 \
1 & 1 & 0 & 0 & 0 \
1 & 0 & 0 & 0 & 0
end{array}
right)=
$$
$$
=frac{1}{3}
left(
begin{array}{rrrrr}
1 & 2 & -1 & -1 & -1 \
1 & -1 & 2 & -1 & -1 \
1 & -1 & -1 & 2 & -1 \
1 & -1 & -1 & -1 & 2 \
-1 & 1 & 1 & 1 & 1
end{array}
right)
left(
begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \
1 & 1 & 1 & 1 & 0 \
1 & 1 & 1 & 0 & 0 \
1 & 1 & 0 & 0 & 0 \
1 & 0 & 0 & 0 & 0
end{array}
right) =
$$
$$
=left(
begin{array}{rrrrr}
0 & 1/3 & 2/3 & 1 & 1/3 \
0 & 1/3 & 2/3 & 0 & 1/3 \
0 & 1/3 & -1/3 & 0 & 1/3 \
0 & -2/3 & -1/3 & 0 & 1/3 \
1 & 2/3 & 1/3 & 0 & -1/3
end{array}
right) .
$$
♦
Т
Теорема. Координаты вектора в старом и новом базисах связаны посредством матрицы перехода $ C_{} $ соотношениями
$$
left{
begin{array}{ccc}
x_1&=&c_{11}{mathfrak x}_1+c_{12}{mathfrak x}_2+dots+c_{1n}{mathfrak x}_n, \
x_2&=&c_{21}{mathfrak x}_1+c_{22}{mathfrak x}_2+dots+c_{2n}{mathfrak x}_n, \
dots& & dots \
x_n&=&c_{n1}{mathfrak x}_1+c_{n2}{mathfrak x}_2+dots+c_{nn}{mathfrak x}_n
end{array}
right.
quad iff quad
left( begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array} right)
=C left( begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array} right) .
$$
Доказательство.
$$
begin{array}{lll}
X=x_1X_1+dots+x_nX_n&=&{mathfrak x}_1{mathfrak X}_1+dots+{mathfrak x}_n{mathfrak X}_n = \
&=&{mathfrak x}_1(c_{11}X_1+c_{21}X_2+dots+c_{n1}X_n)+\
&+&{mathfrak x}_2(c_{12}X_1+c_{22}X_2+dots+c_{n2}X_n)+\
&+& dots +\
&+&{mathfrak x}_n(c_{1n}X_1+c_{2n}X_2+dots+c_{nn}X_n)=\
=(c_{11}{mathfrak x}_1+c_{12}{mathfrak x}_2+dots+c_{1n}{mathfrak x}_n)X_1&+&dots+
(c_{n1}{mathfrak x}_1+c_{n2}{mathfrak x}_2+dots+c_{nn}{mathfrak x}_n)X_n
end{array}
$$
Поскольку при фиксированном базисе координаты вектора определяются однозначно (теорема $ 6 $
☞
ЗДЕСЬ ),
получаем равенства
$$
left{
begin{array}{ccc}
x_1&=&c_{11}{mathfrak x}_1+c_{12}{mathfrak x}_2+dots+c_{1n}{mathfrak x}_n, \
x_2&=&c_{21}{mathfrak x}_1+c_{22}{mathfrak x}_2+dots+c_{2n}{mathfrak x}_n, \
dots& & dots \
x_n&=&c_{n1}{mathfrak x}_1+c_{n2}{mathfrak x}_2+dots+c_{nn}{mathfrak x}_n
end{array}
right.
quad iff quad
left( begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array} right)
=C left( begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array} right)
$$
♦
Практическое значение последнего результата невелико, т.к. нас интересуют именно новые координаты.
=>
Новые координаты выражаются через старые по формуле
$$
left( begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array} right)
=C^{-1} left( begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array} right),
$$
при этом матрицу $ C^{-1} $ можно интерпретировать как матрицу перехода от нового базиса к старому.
?
Пусть в некотором «новейшем» базисе $ { {mathcal X}_1,dots,{mathcal X}_n } $
пространства $ mathbb V_{} $ вектор $ X_{} $ имеет координаты $ (varkappa_1,dots,varkappa_n) $.
Как они связаны с координатами $ (x_{1},dots,x_n) $ в старом базисе $ {X_1,dots,X_n} $, если известны матрица $ C_{} $ перехода от этого базиса к базису $ {{mathfrak X}_1,dots,{mathfrak X}_n } $ и матрица $ D_{} $ перехода от базиса $ {{mathfrak X}_1,dots,{mathfrak X}_n } $ к базису $ {{mathcal X}_1,dots,{mathcal X}_n } $ ?
Евклидовы пространства
— как линейные пространства, в которых вводится понятия угла и расстояния между векторами — рассматриваются
☞
ЗДЕСЬ.
Нормированные пространства
— как линейные пространства, в которых вводится понятие расстояния между векторами — рассматриваются
☞
ЗДЕСЬ.
Линейные отображения
пространств рассматриваются
☞
ЗДЕСЬ
Задачи
Источники
[1]. Лаврентьев М., Люстерник Л. Основы вариационного исчисления. Том 1. Часть I. М.-Л.ОНТИ. 1935, с. 22
[2]. Икрамов Х.Д. Задачник по линейной алгебре. М.1975
[3]. Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969
Пересечение — многообразие
Cтраница 1
Пересечение V многообразия М с В является тогда компактным многообразием и одновременно подполи-эдром В. Следует обратить внимание на несколько обстоятельств.
[1]
Из трансверсальности пересечений многообразий и Х — леммы несложно вывести.
[2]
Очевидным образом определяется пересечение многообразий. Объединением многообразий считается многообразие, порожденное их теоретико-множественным объединением. Относительно этих операций совокупность всех многообразий Ф — алгебр образует полную модулярную решетку. Атомами этой решетки при Ф Z служат многообразия, задаваемые тождествами рх 0 и ху 0 или рх 0 и х х, где р — некоторое простое число. При р 2 получаем многообразие булевых колец. Решетка ft ( 93) антиизоморфна решетке Г — идеалов свободной ЭЗ-алгебры.
[3]
Очевидным образом определяется пересечение многообразий. Объединением многообразий считается многообразие, порожденное их теоретико-множественным объединением. Относительно этих операций совокупность всех многообразий Ф — алгебр образует полную модулярную решетку. Атомами этой решетки при Ф Z служат многообразия, задаваемые тождествами рх О и ху О или рх О и хР х, где р — некоторое простое число. При р 2 получаем многообразие булевых колец. Решетка й ( 33) антиизоморфна решетке Г — идеалов свободной SB-алгебры.
[4]
Поэтому в общем случае пересечение преобразованного многообразия (7.68) и многообразия v3 — О происходит в отдельных точках и без касаний.
[5]
Поэтому в общем случае пересечение преобразованного многообразия (7.68) и многообразия у О происходит в отдельных точках и без касаний.
[6]
Обозначим через Wu ( p, Б) связную компоненту точки р в пересечении многообразия Wu ( p) с шаром радиуса е с центром а точке р; множество W8 ( p Е) определяется аналогично.
[7]
Стоит напомнить, что все предыдущие конструкции кратностей пересечений, за исключением Tor-определения Серра, применимы только в том случае, когда одно из пересекаемых многообразий регулярно вложено в объемлющее пространство. Кратности пересечений произвольных многообразий на неособом многообразии определяются с помощью редукции к диагонали, о чем рассказывается в следующей главе.
[8]
В сечении Пуанкаре некоторой динамической системы или на фазовой плоскости двумерного отображения при наличии двух седловых неподвижных точек может встретиться ситуация, когда устойчивое многообразие одной точки пересекается с неустойчивым многообразием другой. Такая точка пересечения многообразий называется гетероклинической.
[10]
Это соответствует одному из утверждений теоремы Купки-Смейла для диффеоморфизмов. Построенная выше точка р трансверсального пересечения многообразий Ws ( Og g) и Wa ( аа, g) называется трансверсальной гомоклини-ческой точкой.
[11]
Введенное Пуанкаре з вероятностных соображений понятие кинематической меры ( плотности) было развито в интегральной геометрии Сантало и Бляшке, а потом и другими авторами. Это понятие оказалось полезным в применениях интегральной геометрии, когда рассматривается множество пересечений подвижного многообразия с неподвижным. Точные определения и важнейшие — результаты собраны в Лекциях Бляшке и Введении…
[12]
Следует выбрать М трансверсальным к Z и применить ассоциативность произведений-пересечений. Вместе с примерами 8.4.5 и 8.2.6 это показывает, как кратности пересечений на произвольных неособых многообразиях можно определить при помощи кратностей пересечений многообразий дополнительных размерностей в Р, одно из которых к тому же является линейным подпространством.
[13]
Однако теория дифференциально алгебраич. Значительный интерес представляет теория пересечений дифференциально алгебраич. Для них неверно утверждение, что пересечение двух неприводимых многообразий размерности р и д в га-мерном аффинном пространстве имеет размерность но менее р — — д-п. Для порядка пересечения многообразий относительно специальным образом выбираемого базиса получены нек-рые оценки сверху. В частности, можно ввести понятия дифференциально однородных полиномов и проективных дифференциально алгебраич.
[14]
Осознание того, что исчисление Шуберта по существу совпадает с алгеброй многочленов Шура ( появившихся из теории представлений симметрических групп), происходило неоднократно. Джамбелли [ Giambelli 2 ], по-видимому, первым выразил общие детерминанталь-ные множества через такие многочлены. Сами многочлены восходят к Якоби. Явная связь была отмечена Лезье ( [ Lesieur 1 ]) после того, как Эресман ( [ Ehresmann 1 ]) нашел клеточную структуру и кольцо когомо-логий грассманианов, ср. Хорошее представление об этом дают семинары в Страсбурге ( 1976 г.) и Торуни ( 1980 г.) ( ср. Стоит отметить, что хотя многое из этой алгебры восходит к Шуберту, Пьери, Джамбелли и другим классикам алгебраической геометрии, общее правило для пересечения многообразий Шуберта появилось только после правила Литтлвуда — Ричардсона.
[15]
Страницы:
1
2
на алгебраическом многообразии — теория пересечений алгебраич. подмногообразий и циклов. Пусть X — гладкое алгебраич. многообразие размерности пнад полем k, a Yи Z — подмногообразия Xкоразмерности i и j соответственно. Если Yи Zпересекаются транс-версально, то 

Пусть А i (Х) — группа классов алгебраич. циклов коразмерности i на Xпо модулю рациональной эквивалентности; 
Теория пересечений Чжоу состоит из построения трех частей:
а) структуры градуированного коммутативного кольца на (X).для каждого гладкого квазипроективного многообразия X;
б) гомоморфизма градуированных колец 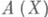
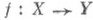
в) гомоморфизма групп 

При этом структуры а), б), в) связаны рядом соотношений, важнейшими из к-рых являются:
формула проекции: для собственного морфизма 

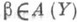

редукция к диагонали: если 


Кроме того, существует естественный гомоморфизм

что позволяет построить теорию Чжэня классов со значениями в кольце Чжоу, и в частности характер Чжэня

являющийся гомоморфизмом колец.
Проще всего определяется гомоморфизм прямого образа f*. Пусть 

где 



где А — локальное кольцо 
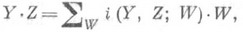
где Wпробегает неприводимые компоненты 
Второй этап — лемма Чжоу о сдвиге — состоит в утверждении, что для произвольных циклов Y, Z на квазипроективном многообразии Xсуществует цикл Z’, рационально эквивалентный Z, к-рый пересекается собственно с Y; более того, класс рациональной эквивалентности 
Наиболее интересен случай проективного многообразия X;применяя функтор прямого образа к структурному морфизму 



Напр., кольцо Чжоу проективного пространства Р n порождается классом гиперплоскости Н, причем 


Для собственно пересекающихся эффективных дивизоров 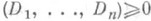
Многими формальными свойствами теории колец Чжоу обладают другие теории: циклы по модулю алгебраической или численной эквивалентности, К-теория, теория сингулярных когомологий 


Лит.:[1] Anneaux de Chow et Applications, Seminaire Chevalley, Seer. Math., P., 1958; [2] Mанин Ю. И., Лекции по алгебраической геометрии, ч. 2, М., 1971; [3] Проблемы Гильберта, М., 1969, с. 175-81; [4] Бальдассари М., Алгебраические многообразия, пер. с англ., М., 1961; [5] Серр Ж. <П., «Математика», 1963, т. 7, с. 3-93; [6] Theorie des intersections et theoreme de Riemann — Roch, В.- Hdlb,- N.Y., 1971; [7l Algebraic geometry, Arcata 1974, Providence, 1975; Xартcхорн Р., Алгебраическая геометрия, пер. с англ., М., 1981.
В. И. Данилов.
Математическая энциклопедия. — М.: Советская энциклопедия.
.
1977—1985.