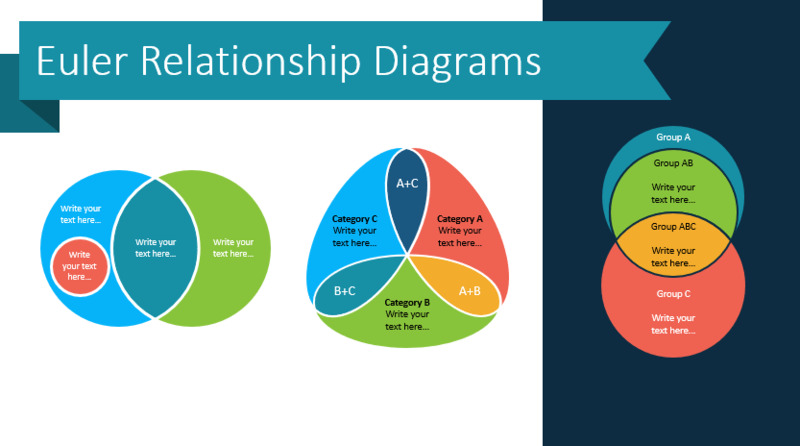
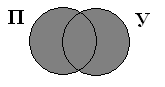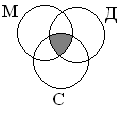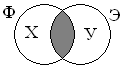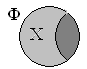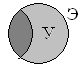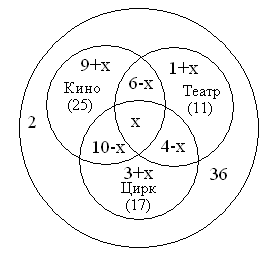Диаграммы Эйлера-Венна
Содержание:
-
Что такое диаграммы Эйлера-Венна
- Принцип построения
- Дополнение множества
- Объединение множеств
- Пересечение множеств
- Симметричная разность множеств
- Разность множеств
- Использование диаграмм Эйлера-Венна для доказательства логических равенств
- Примеры задач с решением
Что такое диаграммы Эйлера-Венна
Определение
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
- В первую очередь необходимо начертить диаграмму, заштриховав все множества, находящиеся в левой части равенства.
- Следующим шагом будет начертание другой диаграммы и штриховка всех множеств, которые находятся в правой части равенства.
- В случае, когда на диаграммах заштрихована одна и та же область, торжество истинно.
Дополнение множества
Дополнением к множеству A является множество (overline A), которое состоит из элементов, не входящих в А.
(overline A;=;left{x;vert;x;notin;Aright})
При этом не все элементы, не являющиеся элементами А, могут быть включены в (overline A.) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение overline A определяется следующим образом:
(overline A;=;U;backslash;A)
Таким образом выглядит дополнение (overline A) графически:
Объединение множеств
Объединением множеств A и B называют множество (A;cup;B), которое состоит из элементов, принадлежащих хотя бы одному из множеств.
Объединение записывается следующим образом:
(A;cup;B;=;left{x;vert;x;in;A;или;x;in:Bright})
Таким образом объединение множеств выглядит графически:
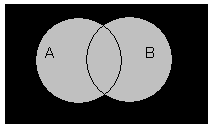
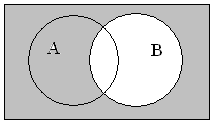
Пересечение множеств
Пересечением множеств A и B является множество (A;cap;B), которое состоит из элементов, входящих в оба множества.
Пересечение множеств записывается следующим образом:
(A;cap;B;=;left{x;vert;x;in;A;и;x;in;Bright})
Таким образом пересечение множеств выглядит графически:
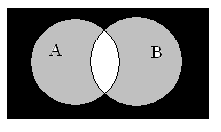
Симметричная разность множеств
Симметричная разность A B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
(Abigtriangleup B=(Abackslash B)cup(Bbackslash A))
Таким образом разность выглядит графически:
Разность множеств
Разностью A B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
(A;backslash;B;=;left{x;vert;x;in;A;и;x;notin;Bright})
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств (A;wedge;B)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
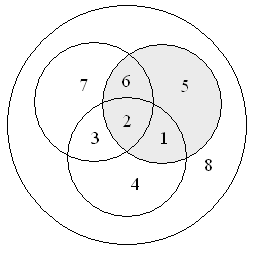
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
(n(U);=;100\n(Р);=;28,;n(Ф);=;42,;n(К);=;30\n;(Р;cap;Ф);=;10,;n(Р;cap;К);=;8,;n;(Ф;cap;К);=;5\n;(Р;cap;Ф;cap;К);=;3)
Необходимо найти (n(Р;cup;Ф;cup;К);=;n;(U;backslash;(Р;cap;Ф;cap:К)))
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в (Р;cap;Ф;cap:К) три элемента, а в множестве (Р;cap;Ф) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
(n(Р;cup;Ф;cup;К);=;13;+;7;+;30;+5;+;3;+;2:+;20;=;80)
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
(n(U;backslash;(Р;cup;Ф;cup;К));=;100;-;80;=;20)
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
- множество задач по алгебре («А»);
- множество задач по геометрии («Г»);
- множество задач по тригонометрии («Т»).
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
Теперь используя диаграмму, обозначим область, которую необходимо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
- Область А = 0, Г = 0, Т = 1: школьников нет.
- Область А = 0, Г = 1, Т = 0: школьников нет.
- Область А = 0, Г = 1, Т = 1: 100 школьников.
- Область А = 1, Г = 0, Т = 0: школьников нет.
- Область А = 1, Г = 0, Т = 1: 200 школьников.
- Область А = 1, Г = 1, Т = 0: 300 школьников.
- Область А = 1, Г = 1, Т = 1: 300 школьников.
Теперь внесем значения всех областей в диаграмму:
Определим x:
(x;=;U;-;(A;cup;Г;cup;Т);)
При U — универсум
U = 1000
((A;cup;Г;cup;Т);=; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900)
x = 1000 — 900 = 100
Ответ: 100 школьников не решило ни одной задачи.
Что это такое? Диаграмма Эйлера кажется чем-то очень сложным на первый взгляд. Однако на самом деле это круги, накладываемые друг на друга при решение определенных задач. Их применяют в алгебре, информатике и даже в жизни, столкнувшись с каким-то выбором.
Как строить? Для начала нужно представить универсальное множество в виде прямоугольника. Внутри него будут эллипсы или круги, которые могут пересекаться, а могут и нет. Их можно дополнять, объединять, пересекать. Давайте рассмотрим все это на примере ниже.
В статье рассказывается:
- Что собой представляет диаграмма Эйлера
- Разница между диаграммой Эйлера и диаграммой Эйлера-Венна
- Задачи, решаемые диаграммой Эйлера
- Принцип построения диаграммы
- Применение диаграмм для доказательства логических равенств
- Пример решения задачи с помощью кругов Эйлера
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Что собой представляет диаграмма Эйлера
Так называется геометрическое изображение, которое используют, чтобы смоделировать множества и схематично отразить отношения между ними. На диаграмме Эйлера наглядно показаны утверждения о данных множествах.
При этом универсальное множество обозначено прямоугольником, а подмножества изображены в виде кругов. Поэтому диаграмму называют также «круги Эйлера». Такое схематичное изображение применяют при решении математических и логических задач, а также в менеджменте и различных прикладных целях.
Автор этого способа – математик XVIII века Леонард Эйлер, который хотел таким образом помочь размышлениям. Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. Диаграмма Эйлера стала признанным методом с момента своего появления.
Биография Леонарда Эйлера связана со Швейцарией, Пруссией и Россией. Этот учёный оказал огромное влияние на развитие математики, механики, физики. Его научные работы (более 850 трудов) затрагивают теорию чисел, теорию музыки, оптику, баллистику, небесную механику. Среди его трудов имеется ряд основополагающих монографий. Около половины жизни Эйлер провёл в России, работал в Петербургской Академии наук и много вложил в развитие российской науки.
Скачать
файл
В дальнейшем в работах многих учёных используется диаграмма Эйлера для множеств: это математики Бернард Больцано и Эрнест Шредер; философ и логик Джон Венн и другие. В наши дни эту методику применяют для развития мышления как при очном обучении, так и на различных онлайн-курсах.
Разница между диаграммой Эйлера и диаграммой Эйлера-Венна
Диаграммы Эйлера-Венна – это частный случай кругов Эйлера, который показывает все 2π{displaystyle 2^{n}} комбинаций π{displaystyle n} свойств, то есть конечную булеву алгебру. При π = 3 диаграмма Эйлера-Венна обычно выглядит как три круга, имеющих одинаковый радиус, их центры совпадают с вершинами равностороннего треугольника, стороне которого приблизительно равны радиусы.
Если определённая комбинация свойств соответствует пустому множеству, на схеме эту область закрашивают. Диаграммы Эйлера могут быть не типичны, а иногда эквивалентны диаграммам Венна. Закрашенный участок схемы указывает на то, что это множество не содержит элементов, то есть пустое.
Задачи, решаемые диаграммой Эйлера
Прикладное значение, которое имеет диаграмма Эйлера: задачи на соотношение множеств в математике, логике, информатике, статистике становятся понятнее при её использовании. Круги Эйлера можно применять и в жизни, находя с их помощью взаимосвязи и отвечая на возникающие насущные вопросы.
Круги Эйлера можно разделить на такие группы:
- равнозначные;
- пересекающиеся;
- подчиненные;
- соподчиненные;
- противоречащие;
- противоположные.

Читайте также
Выполняя упражнения на развитие мышления, чаще всего можно столкнуться с двумя их видами:
- Круги, изображающие объединяющиеся понятия и вложенные один в другой, чтобы это показать.
- Круги, иллюстрирующие пересечения различных множеств, которые имеют те или иные общие признаки.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Уже скачали 20982
Приведём пример использования кругов при выборе профессии. Можно перебирать варианты, обдумывая наиболее подходящий, а можно начертить схему, изобразив в виде кругов то, что вам нравится делать, что вы умеете, и что хорошо оплачивается. Получится диаграмма Эйлера. Пересечение этих трёх кругов и показывает, что будет наиболее вам подходить.
Метод прост в применении и подходит для всех. Его используют и при работе с дошкольниками в детском саду с 4-5 лет, и при обучении студентов (например, можно увидеть подобные задачи в ЕГЭ по информатике), и в научной среде.
Принцип построения диаграммы
При построении диаграммы Эйлера сначала рисуют большой прямоугольник, обозначающий универсальное множество U. Внутри этого прямоугольника располагают фигуры, которые являются изображением множеств: круги (если их не больше трёх) или круги и эллипсы (когда множеств четыре и больше). Фигуры пересекаются различными способами, в зависимости от условий задачи.
Допустим, у нас имеется выражение А. Изображаем на диаграмме круг, обозначающий множество А. Пространство внутри круга показывает значения, при которых выражение А будет истинным, а область снаружи обозначает ложь. Чтобы отобразить на схеме логическую операцию, заштрихуем те части диаграммы, в которых значения истинны. В результате мы отмечаем область, где множества пересекаются.
Можно доказать любой закон алгебры, представив его в виде графической схемы при помощи диаграммы Эйлера. Алгоритм действий таков:
- Сначала чертим диаграмму и заштриховываем все множества, которые находятся с левой стороны от знака «равно».
- Затем нужно начертить другую диаграмму и на ней заштриховать множества, находящиеся справа от знака равенства.
- Если на диаграммах окажется заштрихованной одна и та же область, тождество будет истинным.
Сильнее углубимся в тему.
Дополнение множества
Дополнением к множеству A будет множество Его элементы не относятся к множеству А.
= {x | x ∉ A}
Но в включаются не все элементы, не относящиеся к А. По условиям применения диаграммы Эйлера, все множества, о которых идёт речь в задаче, будут включены в универсальное множество U, то есть являются его подмножествами. С учётом этого дополнение будет определяться так:
=U∖A
Объединение множеств
Объединением двух множеств (назовём их А и В) будет множество A ∪ B, состоящее из элементов, которые включаются хотя бы в одно из них.
Это можно записать так:
A ∪ B={x |x ∈ A или x ∈ B}
Пересечение множеств
Пересечение множеств A и B это множество A ∩ B. Оно состоит из элементов, которые входят и в множество А, и в то же время в множество В.
Только до 29.05
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:



Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Уже скачали 7503
Записывается пересечение множеств так:
A ∩ B = {x | x ∈ A и x ∈ B}
Симметричная разность множеств
Симметричная разность – это множество A B, в которое включаются элементы, которые входят только в одно из множеств А и В, но не в оба сразу.
Запись симметричной разности выглядит таким образом:
A △ B = (A ∖ B) ∪ (B ∖ A)
Разность множеств
Разностью A B являются элементы множества A, не входящие в B.
Записанная разность множеств выглядит так:
A ∖ B = {x | x ∈ A и x ∉ B}
Применение диаграмм для доказательства логических равенств
Давайте рассмотрим, как применяется диаграмма Эйлера на примере доказательства логического равенства.
Представим, что мы имеем конъюнкцию множеств A ∧ B.
Сначала работаем с левой частью равенства. Нужно с помощью диаграммы Эйлера построить множества А и В, заштриховать оба круга цветом и таким образом выделим дизъюнкцию.
Дальше нужно показать инверсию с помощью штриховки области за пределами этих множеств.
Теперь переключаемся на правую часть равенства. Сперва показываем цветной штриховкой за пределами круга А инверсию этого множества.
То же самое действие выполняем для множества В.
Штрихуем чёрным цветом все области пересечения и получаем графическое отображение конъюкции инверсий множеств А и В.
Сравнивая области, отображающие правую и левую части равенства, убеждаемся, что они равны. Таким образом, истинность логического равенства доказана при помощи диаграммы Эйлера.
Пример решения задачи с помощью кругов Эйлера
В демонстрационном тесте ЕГЭ по информатике и ИКТ была представлена задача, которую мы решим с применением этого метода.
Условия задачи:
В языке запросов поискового применяется символ «|» для логической операции «или» и символ «&», чтобы обозначить логическую операцию «и».
Таблица, приведённая ниже, отражает запросы в некотором сегменте сети Интернет и количество найденных страниц по этим запросам.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Вопрос: какое количество страниц (в тысячах) найдётся, если запрос будет сформулирован в виде Крейсер & Линкор?
Принимаем версию, что все запросы выполняются в один отрезок времени, поэтому набор страниц, которые включают искомые слова, остался неизменным.
Решение:
Покажем условие задачи при помощи диаграммы Эйлера. Используем цифры 1, 2 и 3 для обозначения полученных областей.

Читайте также
Используя условия задачи, составляем уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Искомая область Крейсер & Линкор обозначенная на чертеже цифрой 2, находится путём подстановки уравнения (2) в уравнение (1). Получаем следующее:
4800 + 3 = 7000, откуда получаем область 3, равную 2200.
Полученный результат мы подставляем в уравнение (3). Получаем результат:
Область 2 + 2200 = 4500, значит, она равна 2300.
Ответ: будет найдено 2300 страниц по запросу Крейсер & Линкор.
Этот пример показывает, что можно решать с помощью диаграммы Эйлера задачи, являющиеся достаточно сложными или запутанными.
Можно сделать вывод, что круги Эйлера не просто занимательный, но и полезный в плане решения учебных и бытовых задач метод. Многие вещи можно представить в виде множеств, а поможет наглядно представить их пересечение или объединение диаграмма Эйлера.
Любопытно, что современная массовая культура применяет круги Эйлера для создания мемов, а также их можно встретить в таких сериалах, как «Теория большого взрыва» и «4исла».
Советуем применять этот метод для решения задач и непременно поделитесь этим полезным и наглядным способом с друзьями.
(...) — задание скобок; A — отрицание, инверсия, дополнение (NOT); ∪ — дизъюнкция, объединение (OR); ∩ — конъюнкция, пересечение (AND); = — эквивалентность (тождество) (↔); → — импликация (следование); — относительное дополнение (разность); △ — симметрическая разность.
Для вложенного отрицания необходимо использовать знак !. Например, A ∪ B = !(A ∪ B) или A ∪ B = A ∪ !B
Чтобы доказать равенство, например, (AB)C∩B = (AC)(BC), необходимо отдельно ввести (AB)C∩B и (AC)(BC), а затем сравнить их результаты.
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение
).
Здесь будет показано решение
Множества изображаются в виде кругов или эллипсов, помещенных в прямоугольник (универсум).
Рисование кругов Эйлера
С помощью этого инструмента можно будет вручную создавать круги Венна с индивидуальным оформлением. Чтобы заштриховать требуемую область, нажмите на кнопку Заштриховать область, а затем выберите номер области. Для снятия штриховки, повторно нажмите на этот же номер.
Количество переменных (кругов)
Оформление кругов
Цвет линии
Цвет штриховки
Использовать сетку
ABC
(0)(1)(2)(3)(4)(5)(6)(7)
1. Введение
В курсе Информатики и ИКТ основной и старшей
школы рассматриваются такие важные темы как
“Основы логики” и “Поиск информации в
Интернет”. При решении определенного типа задач
удобно использовать круги Эйлера (диаграммы
Эйлера-Венна).
Математическая справка. Диаграммы Эйлера-Венна
используются прежде всего в теории множеств как
схематичное изображение всех возможных
пересечений нескольких множеств. В общем случае
они изображают все 2n комбинаций n свойств.
Например, при n=3 диаграмма Эйлера-Венна обычно
изображается в виде трех кругов с центрами в
вершинах равностороннего треугольника и
одинаковым радиусом, приблизительно равным
длине стороны треугольника.
2. Представление логических связок в поисковых
запросах
При изучении темы “Поиск информации в
Интернет” рассматриваются примеры поисковых
запросов с использованием логических связок,
аналогичным по смыслу союзам “и”, “или”
русского языка. Смысл логических связок
становится более понятным, если
проиллюстрировать их с помощью графической
схемы – кругов Эйлера (диаграмм Эйлера-Венна).
| Логическая связка | Пример запроса | Пояснение | Круги Эйлера |
| & — “И” | Париж & университет | Будут отобраны все страницы, где упоминаются оба слова: Париж и университет |
Рис.1
|
| | — “ИЛИ” | Париж | университет | Будут отобраны все страницы, где упоминаются слова Париж и/или университет |
Рис.2
|
3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно наглядно
представить связь логических операций с теорией
множеств. Для демонстрации можно
воспользоваться слайдами в Приложение
1.
Логические операции задаются своими таблицами
истинности. В Приложении 2
подробно рассматриваются графические
иллюстрации логических операций вместе с их
таблицами истинности. Поясним принцип
построения диаграммы в общем случае. На
диаграмме – область круга с именем А отображает
истинность высказывания А (в теории множеств
круг А – обозначение всех элементов, входящих в
данное множество). Соответственно, область вне
круга отображает значение “ложь”
соответствующего высказывания. Что бы понять
какая область диаграммы будет отображением
логической операции нужно заштриховать только
те области, в которых значения логической
операции на наборах A и B равны “истина”.
Например, значение импликации равно “истина”
в трех случаях (00, 01 и 11). Заштрихуем
последовательно: 1) область вне двух
пересекающихся кругов, которая соответствует
значениям А=0, В=0; 2) область, относящуюся только к
кругу В (полумесяц), которая соответствует
значениям А=0, В=1; 3) область, относящуюся и к кругу
А и к кругу В (пересечение) – соответствует
значениям А=1, В=1. Объединение этих трех областей
и будет графическим представлением логической
операции импликации.
4. Использование кругов Эйлера при
доказательстве логических равенств (законов)
Для того, чтобы доказать логические равенства
можно применить метод диаграмм Эйлера-Венна.
Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон
де Моргана).
Для наглядного представления левой части
равенства выполним последовательно:
заштрихуем оба круга (применим дизъюнкцию) серым
цветом, затем для отображения инверсии
заштрихуем область за пределами кругов черным
цветом:
Рис.3 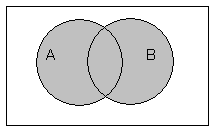
Для визуального представления правой части
равенства выполним последовательно:
заштрихуем область для отображения инверсии (¬А)
серым цветом и аналогично область ¬В также серым
цветом; затем для отображения конъюнкции нужно
взять пересечение этих серых областей (результат
наложения представлен черным цветом):
Рис.5 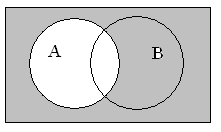
Видим, что области для отображения левой и
правой части равны. Что и требовалось доказать.
5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск
информации в Интернет”
Задача №18 из демо-версии ГИА 2013.
В таблице приведены запросы к поисковому
серверу. Для каждого запроса указан его код –
соответствующая буква от А до Г. Расположите коды
запросов слева направо в порядке убывания количества
страниц, которые найдет поисковый сервер по
каждому запросу.
| Код | Запрос |
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Решение:
Для каждого запроса построим диаграмму
Эйлера-Венна:
| Запрос А
Рис.8 |
Запрос Б
Рис. 9 |
Запрос В
Рис. 10 |
Запрос Г
Рис. 11 |
Ответ: ВАГБ.
Задача В12 из демо-версии ЕГЭ-2013.
В таблице приведены запросы и количество
найденных по ним страниц некоторого сегмента
сети Интернет.
| Запрос | Найдено страниц (в тысяч) |
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет
найдено по запросу Эсминец?
Считается, что все запросы выполнялись
практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за
время выполнения запросов.
Решение:
Пусть
Ф – количество страниц (в тысячах) по запросу Фрегат;
Э – количество страниц (в тысячах) по запросу Эсминец;
Х – количество страниц (в тысячах) по запросу, в
котором упоминается Фрегат и не упоминается
Эсминец;
У – количество страниц (в тысячах) по запросу, в
котором упоминается Эсминец и не
упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого
запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12
|
3400 |
| Фрегат & Эсминец | Рис.13
|
900 |
| Фрегат | Рис.14
|
2100 |
| Эсминец | Рис.15
|
? |
Согласно диаграммам имеем:
- Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
- Э = 900+У = 900+1300= 2200.
Ответ: 2200.
6. Решение логических содержательных
задач методом диаграмм Эйлера-Венна
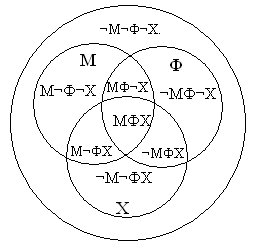
Задача 1.
В классе 36 человек. Ученики этого класса
посещают математический, физический и
химический кружки, причем математический кружок
посещают 18 человек, физический — 14 человек,
химический — 10. Кроме того, известно, что 2
человека посещают все три кружка, 8 человек — и
математический и физический, 5 и математический и
химический, 3 — и физический и химический.
Сколько учеников класса не посещают никаких
кружков?
Решение:
Для решения данной задачи очень удобным и
наглядным является использование кругов Эйлера.
Самый большой круг – множество всех учеников
класса. Внутри круга три пересекающихся
множества: членов математического (М),
физического (Ф), химического (Х) кружков.
Пусть МФХ – множество ребят, каждый из
которых посещает все три кружка. МФ¬Х –
множество ребят, каждый из которых посещает
математический и физический кружки и не
посещает химический. ¬М¬ФХ — множество ребят,
каждый из которых посещает химический кружок и
не посещает физический и математический кружки.
Аналогично введем множества: ¬МФХ, М¬ФХ,
М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Известно, что все три кружка посещают 2
человека, следовательно, в область МФХ впишем
число 2. Т.к. 8 человек посещают и математический и
физический кружки и среди них уже есть 2 человека,
посещающих все три кружка, то в область МФ¬Х впишем
6 человек (8-2). Аналогично определим количество
учащихся в остальных множествах:
| Круги Эйлера с названиями непересекающихся множеств: Рис. 16 |
Круги Эйлера с количественной информацией: Рис. 17 Например, количество человек, которые посещают |
Просуммируем количество человек по всем
областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из
класса посещают кружки.
Значит, 36-28 = 8 учеников не посещают кружки.
Ответ: 8.
Задача 2.
После зимних каникул классный руководитель
спросил, кто из ребят ходил в театр, кино или цирк.
Оказалось, что из 36 учеников класса двое не были
ни в кино. ни в театре, ни в цирке. В кино побывало
25 человек, в театре — 11, в цирке 17 человек; и в кино,
и в театре — 6; и в кино и в цирке — 10; и в театре и в
цирке — 4.
Сколько человек побывало и в кино, и в театре, и
в цирке?
Решение:
Пусть х – количество ребят, которые побывали и
в кино, и в театре, и в цирке.
Тогда можно построить следующую диаграмму и
посчитать количество ребят в каждой области:
|
Рис.18. |
В кино и театре побывало 6 чел., значит, только в кино и театре (6-х) чел. Аналогично, Только в театре и цирке (4-х) чел. В кино побывало 25 чел., значит, из них только в Аналогично, только в театре были (1+х) чел. Только в цирке были (3+х) чел. Не были в театре, кино и цирке – 2 чел. Значит, 36-2=34 чел. побывали на мероприятиях. С другой стороны можем просуммировать (9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34 33+х = 34. Отсюда следует, что только один человек побывал |
Ответ: 1.
Таким образом, круги Эйлера (диаграммы
Эйлера-Венна) находят практическое применение
при решении задач в формате ЕГЭ и ГИА и при
решении содержательных логических задач.
Литература
- В.Ю. Лыскова, Е.А. Ракитина. Логика в информатике.
М.: Информатика и Образование, 2006. 155 с. - Л.Л. Босова. Арифметические и логические основы
ЭВМ. М.: Информатика и образование, 2000. 207 с. - Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и
ИКТ для 8 класса: БИНОМ. Лаборатория знаний, 2012. 220
с. - Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и
ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244
с. - Сайт ФИПИ: http://www.fipi.ru/
Операции над событиями. Диаграммы Эйлера – Венна
Содержание
В теории вероятностей случайными событиями являются подмножества множества элементарных исходов Ω .
Над событиями, как и над любыми множествами, можно совершать следующие операции.
Произведение (пересечение) двух событий
Операцию произведения (пересечения) двух событий A и B обозначают
, или AB, или
.
ОПРЕДЕЛЕНИЕ 1. Произведением (пересечением) двух событий A и B называют такое событие, которое состоит из всех элементов, входящих как в событие A , так и в событие B (рис. 1).
Рис.1
Сумма (объединение) двух событий
Операцию суммы (объединения) двух событий A и B обозначают
A + B или
ОПРЕДЕЛЕНИЕ 2. Суммой (объединением) двух событий A и B называют такое событие, которое состоит из элементов события A и элементов события B (рис. 2).
Рис.2
Разность двух событий
Операцию разности двух событий A и B обозначают
A B
ОПРЕДЕЛЕНИЕ 3. Разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B (рис. 3).
Рис.3
ЗАМЕЧАНИЕ 1. Разностью событий B и A является событие B A , изображенное на рисунке 4.
Рис.4
Симметрическая разность двух событий
Операцию симметрической разности двух событий A и B обозначают
ОПРЕДЕЛЕНИЕ 4 . Симметрической разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B , а также из тех элементов события B , которые не входят в событие A (рис. 5).
Рис.5
Переход к противоположному событию
Событие, противоположное к событию A , обозначают
или AC
ОПРЕДЕЛЕНИЕ 5. Противоположным событием к событию A называют событие, состоящее из тех элементов всего множества элементарных событий Ω , которые не входят в событие A (рис. 6).
Рис.6
ЗАМЕЧАНИЕ 2. Справедлива формула
ОПРЕДЕЛЕНИЕ 6. Событие Ω называют достоверным событием, пустое множество называют невозможным событием.
ЗАМЕЧАНИЕ 3. Рисунки, на которых наглядно показаны операции над множествами, называют диаграммами Эйлера-Венна. В частности, диаграммами Эйлера-Венна являются рисунки 1-6 .