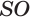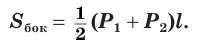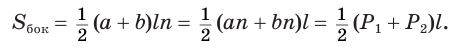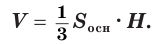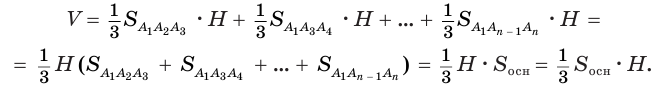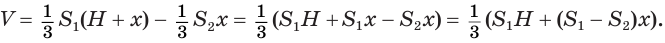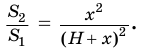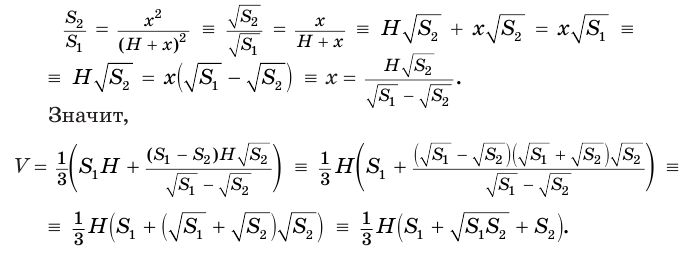Пирамида
Выпишите номера рисунков, на которых изображены
1) пирамиды
2) правильные пирамиды
3) четырехугольные пирамиды
Номера необходимо указать в порядке возрастания без пробелов и запятых. Например, 234.
Пирамида
Найдите пару для каждой пирамиды.
Обратите внимание на многоугольники, лежащие в основаниях пирамид
Пирамида
Что представляет собой боковая грань пирамиды?
Вспомните определение пирамиды и примеры, которые были приведены на уроке.
|
параллелограмм |
|
|
треугольник |
|
|
прямоугольник |
|
|
четырехугольник |
Пирамида
Добавьте подписи на изображении
Вспомните определения вершины, основания, бокового ребра, боковой грани и высоты пирамиды.
высота
боковая грань
основание
вершина
боковое ребро
Пирамида
Решите кроссворд
Вспомните определения и примеры, которые были разобраны на уроке. В вопросе №4 вспомните известные вам пирамиды, мысленно попытайтесь представить каждую из граней в роли основания.
Пирамида
Вставьте правильный вариант ответа
Вспомните, что называется площадью боковой поверхности и площадью полной поверхности пирамиды.
Площадь боковой поверхности правильной пирамиды равна половине произведения
основания на
. Площадь полной поверхности правильной пирамиды вычисляется как сумма площади
и площади
.
Пирамида
Зачеркните неверные утверждения
Вспомните, какая пирамида называется правильной.
1) Пирамида называется правильной, если в основании лежит правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
2) Площадь поверхности правильной пирамиды – это сумма площадей боковых граней.
3) Основание правильной пирамиды – правильный многоугольник.
4) Прямая пирамида называется правильной, если в основании лежит правильный многоугольник.
Пирамида
Ответьте на вопросы:
Вспомните формулы для вычисления площади боковой поверхности и полной поверхности пирамиды.
Пирамида
Площадь боковой поверхности какой пирамиды можно вычислить по формуле
$S_{бок} = ½·P_{осн}·l_{апоф}$
Вспомните, для какой пирамиды выведена данная формула. Как отличить данный вид пирамиды на изображении?
Пирамида
Ответьте на вопросы
Нарисуйте изображение нескольких пирамид. Какая закономерность есть между числом боковых ребер и общим числом ребер, а также вершинами многоугольника в основании?
Пирамида
Установите правильный порядок в решении задачи.
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Подумайте, как бы вы решали данную задачу. Представьте план решения на листочке, а затем соотнесите его с текстом задания.
Периметр основания равен сумме всех сторон. Поскольку в основании правильный шестиугольник со стороной 10, то периметр равен 60.
[l=sqrt{13^{2}-5^{2}}=12]
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему, то есть равен ½ · 60 · 12 = 360.
Найдем апофему по теореме Пифагора как катет прямоугольного треугольника, гипотенуза которого – боковое ребро, а другой катет – половина стороны основания.
[l=sqrt{13^{2}-5^{2}}=12]
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему, то есть равен ½ · 60 · 12 = 360.
Найдем апофему по теореме Пифагора как катет прямоугольного треугольника, гипотенуза которого – боковое ребро, а другой катет – половина стороны основания.
Периметр основания равен сумме всех сторон. Поскольку в основании правильный шестиугольник со стороной 10, то периметр равен 60.
Пирамида
Ответьте на вопросы
Какой треугольник образован боковым ребром и высотой пирамиды?
Пирамида
Заполните пропуски в тексте
Сделайте изображение какой-нибудь правильной пирамиды. Какие треугольники будут равны при таких условиях?
Если вершина пирамиды проецируется в центр описанной около основания окружности, то равны
. Если вершина пирамиды проецируется в центр вписанной в основание окружности, то равны
.
Пирамида
Основаниями усеченной пирамиды являются правильные треугольники со сторонами 5 и 3. Одно из боковых ребер перпендикулярно к плоскости основания и равно 1. Найдите площадь боковой поверхности усеченной пирамиды.
Вспомните, какая пирамида называется усеченной. По какой формуле вычисляется площадь боковой поверхности усеченной пирамиды?
Пирамида
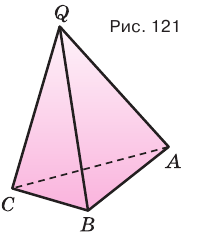
Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.
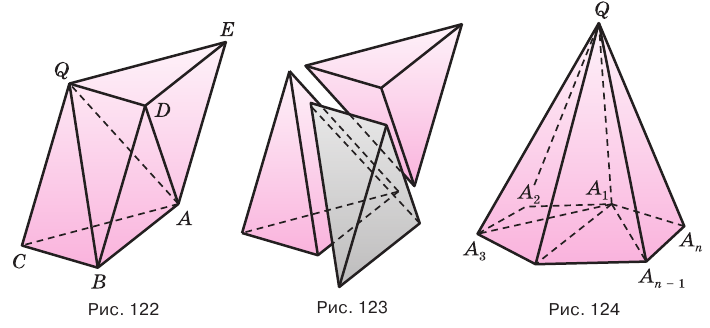
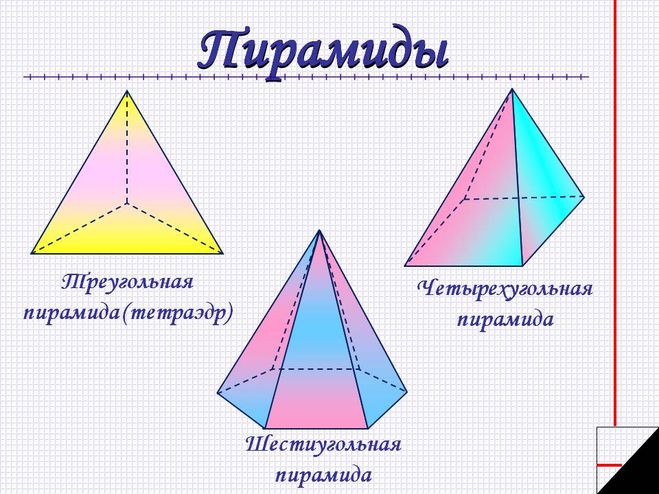
По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное.
Виды пирамид
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Узнать ещё
Знание — сила. Познавательная информация
Пирамиды, в которых все боковые ребра равны
Рассмотрим свойства пирамид, в которых все боковые ребра равны, с соответствующими чертежами.
Если все боковые ребра пирамиды равны между собой, то вершина пирамиды проецируется в центр описанной около основания окружности.
Прямоугольные треугольники, образованные высотой пирамиды, боковыми ребрами и их проекциями (равными радиусу описанной окружности), равны. Поэтому также
— все боковые ребра пирамиды образуют с плоскостью основания равные углы;
— все углы, которые боковые ребра образуют с высотой пирамиды, равны.
Решение задач на пирамиду, в которой все боковые ребра равны (либо все боковые ребра образуют равные углы с основанием пирамиды или с высотой пирамиды) начинается с чертежа.
Если основание пирамиды — треугольник.
Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника.
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника.
На рисунке тупой угол — это угол B.
Радиус окружности, описанной около произвольного остроугольного либо тупоугольного треугольника ABC, можно найти по следствию из теоремы синусов:
либо по формуле
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
Радиус описанной около основания окружности в этом случае равен
где c — гипотенуза.
Отсюда для данного треугольника ABC с прямым углом B
Если основание пирамиды — параллелограмм
Из всех параллелограммов описать окружность можем только около прямоугольника (квадрат — его частный случай). Поэтому, если в задаче сказано, что пирамиде все боковые ребра равны, либо все боковые ребра одинаково наклонены к плоскости основания, либо все боковые ребра образуют с высотой пирамиды равные углы, а в основании — параллелограмм, то это может быть только прямоугольник (квадрат).
Центр описанной около прямоугольника окружности — точка пересечения его диагоналей. Соответственно, радиус R равен половине диагонали прямоугольника.
Если основание пирамиды -трапеция
Из всех трапеций описать окружность можно только около равнобочной трапеции.
Радиус описанной окружности ищем как радиус окружности, описанной около одного из треугольников ABC или ACD по одной из формул, приведенных выше.
Если диагональ трапеции перпендикулярна боковой стороне
боковые ребра пирамиды равны
В этом случае центр описанной около трапеции окружности лежит на середине большего основания, а высота пирамиды лежит в боковой грани, содержащей это большее основание.
Радиус R в этом случае — половина гипотенузы прямоугольного треугольника ACD.
Если основание пирамиды — произвольный четырехугольник
Радиус описанной около основания окружности находим как радиус окружности, описанной около одного из треугольников основания: ABC, BCD, ACD или ABD.
Поскольку описать около четырехугольника окружность можно только тогда, когда сумма его противолежащих углов равна 180 градусов, то
Геометрия. 10 класс
Пирамида
Выпишите номера рисунков, на которых изображены
2) правильные пирамиды
3) четырехугольные пирамиды
Номера необходимо указать в порядке возрастания без пробелов и запятых. Например, 234.
Пирамида
Найдите пару для каждой пирамиды.
Пирамида
Что представляет собой боковая грань пирамиды?
Пирамида
Добавьте подписи на изображении
Пирамида
Пирамида
Вставьте правильный вариант ответа
Площадь боковой поверхности правильной пирамиды равна половине произведения основания на . Площадь полной поверхности правильной пирамиды вычисляется как сумма площади и площади .
Пирамида
Зачеркните неверные утверждения
1 ) Пирамида называется правильной, если в основании лежит правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
2 ) Площадь поверхности правильной пирамиды – это сумма площадей боковых граней.
3 ) Основание правильной пирамиды – правильный многоугольник.
4 ) Прямая пирамида называется правильной, если в основании лежит правильный многоугольник.
http://resh.edu.ru/subject/lesson/5866/train/221585/
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
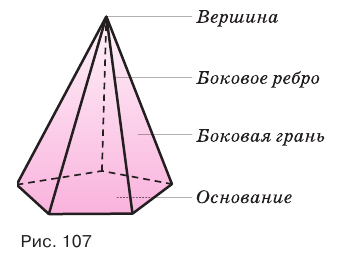
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота
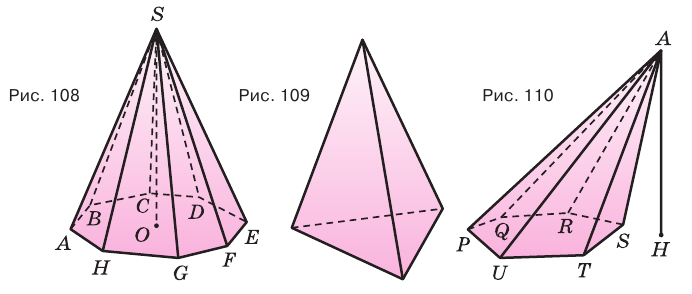
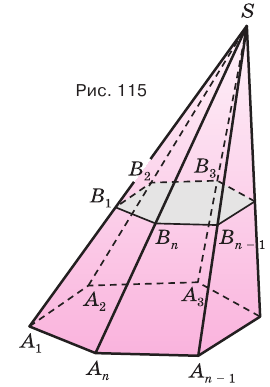
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
- боковые ребра равны;
- боковые грани равны;
- апофемы, равны;
- двугранные углы при основании равны;
- двугранные углы при боковых ребрах равны;
- каждая точка высоты равноудалена от вершин основания;
- каждая точка высоты равноудалена от ребер основания;
- каждая точка высоты равноудалена от боковых граней.
Отметим, что если в пирамиде равны все:
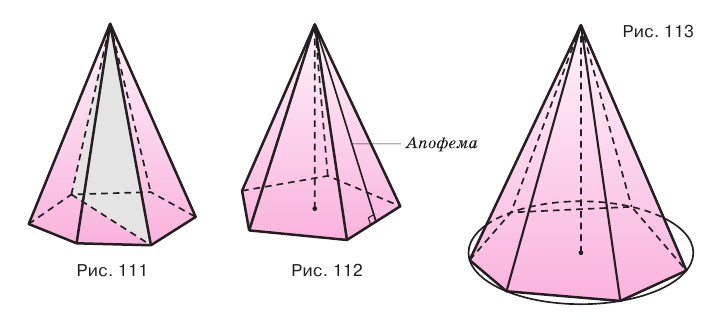
- боковые ребра, то около ее основания можно описать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 113);
- двугранные углы при основании, то в это основание можно вписать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 114).
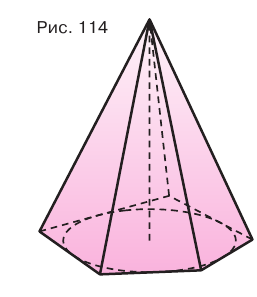
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
Если пирамиду пересечь плоскостью, параллельной основанию, то:
- а) боковые ребра и высота разделяются на пропорциональные части;
- б) в сечении получается многоугольник, подобный основанию;
- в) площади сечения и основания относятся как квадраты их расстояний от вершины пирамиды.
Используя рисунок 115, докажите эту теорему самостоятельно.
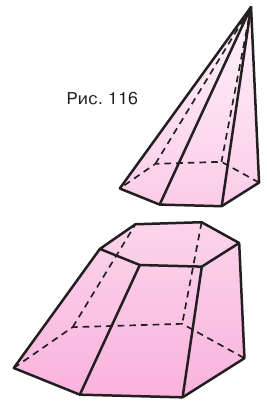
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
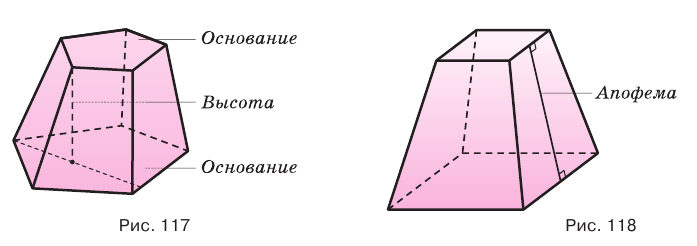
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
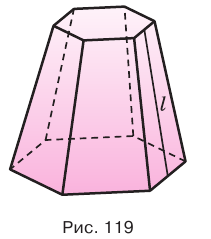
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
Доказательство:
Пусть есть правильная 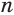
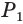
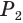
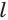
Боковая поверхность данной пирамиды состоит из 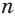
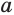
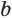
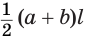
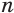
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
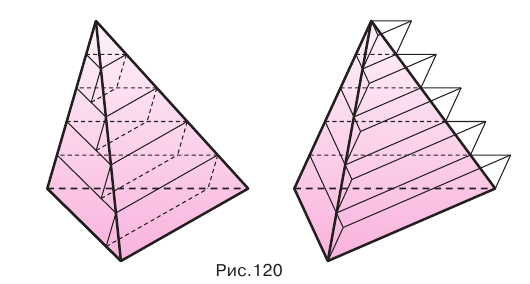
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство:
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 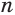
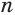
Пусть 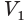
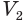


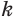
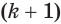


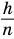
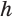
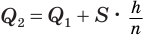
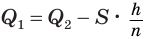
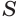
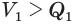
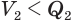
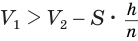
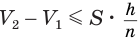
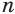
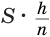
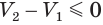
Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство
Из неравенств (1) и (2) следует, что 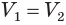
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
Доказательство:
Пусть есть треугольная пирамида 

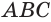
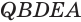
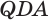


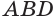
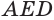




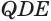

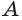
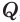





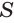

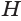



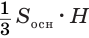
Пусть теперь есть произвольная пирамида 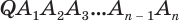
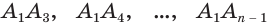
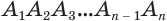
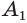
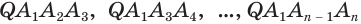

Пример:
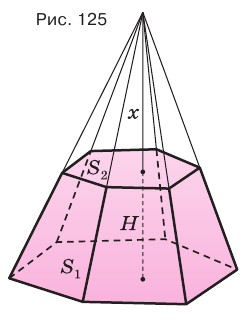
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 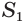
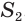

Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 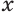
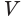
Чтобы найти высоту 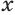
Решим это уравнение, учитывая, что 

Таким образом, объем 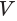
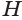


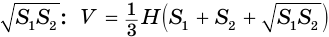
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Стереометрия — формулы, определение и вычисление
1
Как изобразить по две подобные пирамиды?
1 ответ:
0
0
Думаю для того, чтобы изобразить подобные пирамиды в призме нужно начертить две призмы со сторонами оснований и высотами в соотношении 2:5 и потом нарисовать внутри них пирамиды. Эти пирамиды тоже будут подобны с таким же коэффициентом.
Читайте также
Искомый угол равен арксинусу отношения расстояния h от точки А до плоскости РВС к длине ребра АР, то есть arcsin(h/2).
Расстояние h равно высоте треугольной пирамиды АРВС с основанием РВС.
Объём пирамиды АРВС равен половине объёма пирамиды РАВСD:
(2*2*2^(1/2)/3)/2 = 2*2^(1/2)/3.
С другой стороны объём пирамиды АРВС равен делённому на 3 произведению h на площадь равностороннего треугольника со стороной 2:
h*3^(1/2)/3 = h/3^(1/2) и, значит,
h = 2*6^(1/2)/3, откуда искомый угол:
arcsin(h/2) = arcsin(6^(1/2)/3).
Ответ: (Б) arcsin(6^(1/2)/3).
Чтобы найти объём тетраэдра PBCD, надо разделить надвое объём пирамиды PABCD, потому что BD — диагональ квадрата ABCD, а значит, треугольник PBD делит пирамиду надвое.
Итак, находим объём пирамиды. Как известно, это треть от произведения площади основания ABCD на длину высоты PО. Ну площадь основания найти легко, это 4 см в квадрате. Трудности начинаются с нахождения высоты, но и тут решить можно, при помощи теоремы Пифагора (квадрат гипотенузы равен квадратам катетов).
Итак, находим прежде всего, отрезок АО — половину от гипотенузы АС. Он равен √(АВ² + AC²)/2 = √2.
Теперь находим отрезок РО — высоту пирамиды и по совместительству катет треугольника АОР. Он равен √(AP² — AO²) = √2
Умножаем теперь √2 на 4 и делим на 3. Получаем 4√2/3. Это — объём целой пирамиды.
Делим объём пирамиды на 2 — и получаем искомый объём тетраэдра.
Ответ Б.
Пирамида представляет собой многогранник.Основанием является многоугольник,а грани остальные-треугольник,которые имеют общую вершину.Разные пирамиды бывают — четырехугольные,треугольные и шестиугольные.
Потому что листы бумаги прямоугольные и таблицы на них привычно рисовать прямоугольные.
Потому что в «пирамиде» есть 2х9, но нет 9х2.
Я-то понимаю что разницы нет, а вот нуб зубрящий таблицу, может впасть в ступор.
Нет. У пирамиды всегда четное количество ребер.
В основании лежит n-угольник, он имеет n углов (неожиданно, правда? :)) и n ребер.
И 1 вершину, к которой идет еще n ребер из этих n углов в основании.
Поэтому, если в основании пирамиды лежит n-угольник, то вся пирамида имеет 2n ребер.
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
- Определение пирамиды
- Элементы пирамиды
- Виды сечения пирамиды
- Виды пирамид
Определение пирамиды
Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.
Примечание: пирамида – это частный случай конуса.
Элементы пирамиды
Для рисунка выше:
- Основание (четырехугольник ABCD) – грань фигуры, являющая многогранником. Ей не принадлежит вершина.
- Вершина пирамиды (точка E) – общая точка всех боковых граней.
- Боковые грани – треугольники, которые сходятся в вершине. В нашем случае это: AEB, AED, BEC и CED.
- Боковые ребра – стороны боковых граней, за исключением тех, которые принадлежат основанию. Т.е. это AE, BE, CE и DE.
- Высота пирамиды (EF или h) – перпендикуляр, опущенный из вершины пирамиды на ее основание.
- Высота боковой грани (EM) – высота треугольника, являющегося боковой гранью фигуры. В правильной пирамиде называются апофемой.
- Площадь поверхности пирамиды – площадь основания и всех ее боковых граней. Формулы для нахождения площади поверхности (правильной фигуры), а также объема пирамиды представлены в отдельных публикациях.
Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.
Примечание: свойства пирамиды представлены в отдельной публикации.
Виды сечения пирамиды
1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):
2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.
На данном рисунке:
- пирамиды EABCD и EA1B1C1D1 подобны;
- четырехугольники ABCD и A1B1C1D1 также подобны.
Примечание: Существуют и другие виды сечения, но они не так распространены.
Виды пирамид
- Правильная пирамида – основанием фигуры является правильный многоугольник, а ее вершина проецируется в центр основания. Может быть треугольной, четырехугольной (на рисунке ниже), пятиугольной, шестиугольной и т.д.
- Пирамида с боковым ребром, перпендикулярным основанию – одно из боковых ребер фигуры расположено под прямым углом к плоскости основания. В этом случае данное ребро является высотой пирамиды.
- Усеченная пирамида – часть пирамиды, оставшаяся между ее основанием и параллельной этому основанию секущей плоскостью.
- Тетраэдр – это треугольная пирамида, гранями которой являются 4 треугольника, каждый из которых может быть принят за основание. Является правильным (как на рисунке ниже) – если все ребра равны, т.е. все грани – это равносторонние треугольники.