Углы при пересечении двух прямых
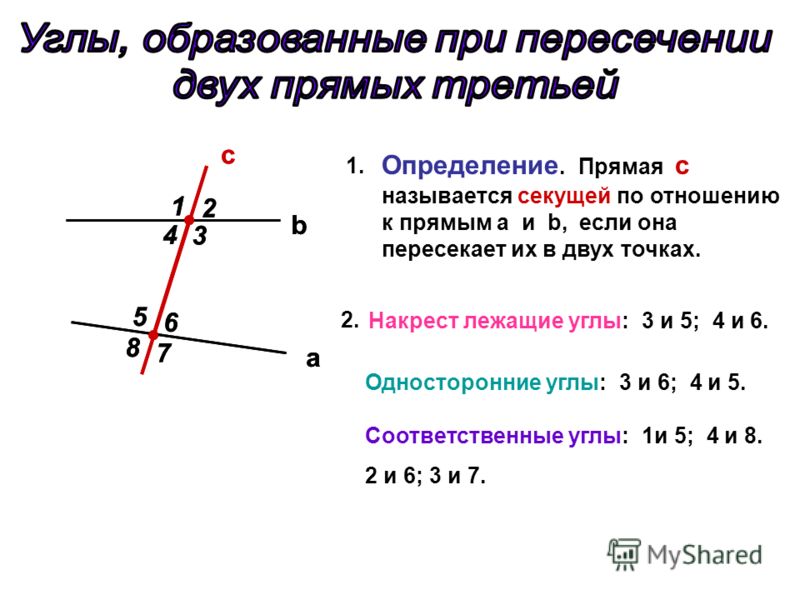
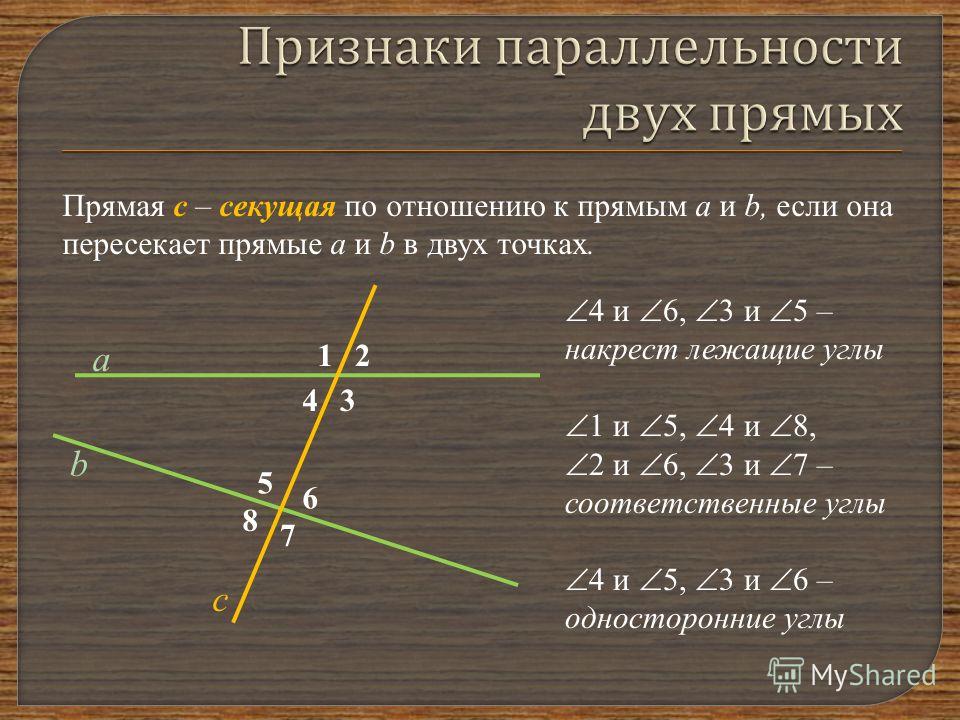
Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.
При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.
На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).
Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:
Углы при пересечении параллельных прямых
Если секущая пересекает две параллельные прямые линии, то:
- внутренние накрест лежащие углы равны;
- сумма внутренних односторонних углов равна 180°;
- соответственные углы равны;
- внешние накрест лежащие углы равны;
- сумма внешних односторонних углов равна 180°.
Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.
Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть
Конечно, углы и , и — тоже вертикальные.
Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .
Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.
Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть
Углы и (а также и , и , и ) называются соответственными.
Соответственные углы равны, то есть
Углы и (а также и , и , и ) называют накрест лежащими.
Накрест лежащие углы равны, то есть
Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.
Ты нашел то, что искал? Поделись с друзьями!
1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .
Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.
Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.
Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .
Периметр параллелограмма — это сумма всех его сторон, то есть
2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.
Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .
3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.
Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.
Давайте посмотрим на чертеж. По условию, , то есть .
Углы и — односторонние при параллельных прямых и секущей, следовательно,
Геометрия. Урок 2. Углы
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Углы
Понятие угла
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.
Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B или ∠ B O A , но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O .
Величину угла измеряют в градусах. ∠ A O B = 24 ° .
Виды углов:
Биссектриса угла
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла.
∠ A O D = ∠ B O D = ∠ A O B 2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B .
Углы, образованные при пересечении двух прямых
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180 ° .
( 1 ) и ( 3 )
( 2 ) и ( 4 )
называются вертикальными .
По свойству вертикальных углов:
∠ C O D = ∠ A O B
∠ B O D = ∠ A O C
( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )
называются смежными .
По свойству смежных углов:
∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °
Углы, образованные при пересечении двух прямых секущей
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )
называются соответственными .
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
( 3 ) и ( 5 )
( 4 ) и ( 6 )
называются внутренними односторонними .
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
( 1 ) и ( 7 )
( 2 ) и ( 8 )
называются внешними односторонними .
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
( 3 ) и ( 6 )
( 4 ) и ( 5 )
называются внутренними накрест лежащими .
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
( 1 ) и ( 8 )
( 2 ) и ( 7 )
называются внешними накрест лежащими .
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны , то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180 ° .
- Сумма внешних односторонних углов равна 180 ° .
Сумма углов многоугольника
Сумма углов произвольного n -угольника вычисляется по формуле:
S n = 180 ° ⋅ ( n − 2 )
где n – это количество углов в n -угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.
Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °
Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °
Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:
Чтобы найти величину угла правильного n -угольника , необходимо сумму углов этого многоугольника разделить на количество углов.
α n = 180 ° ⋅ ( n − 2 ) n
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с углами
http://ege-study.ru/ru/ege/materialy/matematika/ugly-pri-parallelnyx-pryamyx/
Пары углов, образованные параллельными прямыми, пересеченными секущей
Когда есть две параллельные линии (на рисунке внизу), можно выделить две основные области: внутреннюю и внешнюю.
Когда две параллельные линии пересекаются третьей прямой, эта прямая называется секущей. В примере, приведенном ниже, образуются восемь углов, когда параллельные линии m и n пересекаются секущей — прямой t.
Есть несколько пар углов, образованных на этом рисунке. Некоторые пары уже рассмотрены:
Вертикальные пары: 1 и 4
2 и 3
5 и 8
6 и 7
Напомним, что все пары вертикальных углов равны.
Смежные углы: 1 и 2
2 и 4
3 и 4
1 и 3
5 и 6
6 and 8
7 and 8
5 and 7
Напомним, что смежные углы это углы, которые дополняют друг друга до 180°. Все эти смежные пары есть линейными парами. Есть и другие пары смежных углов, которые описаны далее в этом разделе. Есть еще три специальные пары углов. Эти пары есть конгруэнтными (равными) парами.
Внутренние накрест лежащие углы это два угла во внутренней области параллельных прямых и на разных сторонах секущей. Внутренние накрест лежащие углы попарно равны.
Внешние накрест лежащие углы это два угла во внешней области параллельных прямых и на разных сторонах секущей. Внешние накрест лежащие углы попарно равны.
Соответственные углы это два угла, один во внешней области, один во внутренней области, и которые лежат на одной стороне секущей. Соответственные углы равны.
Используйте следующие диаграмма параллельных линий, пересеченных секущей, чтобы дать ответы на вопросы в примерах.
Пример:
Чему равен угол 8?
Угол, величина которого на рисунке равна 53° и 8 — внешние накрест лежащие углы.
Так как такие углы являются равными, то величина 8 = 53°.
Пример:
Чему равен угол 7?
8 и 7 есть линейной парой; они смежные. Они дополняют друг друга до 180°. Поэтому, 7 = 180° – 53° = 127°.
1. Когда секущая пересекает параллельные прямые, все образующиеся при этом острые углы равны, и все образующиеся тупые углы- равны.
На рисунку вверху1, 4, 5, и 7 есть острыми углами. Они все равны между собой. 1 ≅ 4 есть вертикальными углами. 4 ≅ 5 есть внутренним накрест лежащими углами, и 5 ≅ 7 — вертикальные углы. То же свойство и справедливо для тупых углов на рисунке: 2, 3, 6, и 8 есть равными между собой.
2. Когда секущая пересекает параллельные прямые, один любой образующийся угол и один любой образующийся тупой угол есть смежными.
На рисунке Вы можете видеть, что 3 и 4 являются смежными, потому что они есть линейной парой. Обратите внимание, что 3 ≅ 7, так как они есть соответсвенными углами. Поэтому, вы можете заменить 7 на 3 и знать, что 7 и 4 есть смежными.
Пример:
На рисунке внизу изображены две параллельные прямые, пересечённые секущей. Какой из пронумерованных углов является смежным к углу 1?
Угол, смежный 1 есть 6. 1 является тупым углом, а как мы помним, любой острый угол является смежным любому тупому углу. Но на рисунке пронумерован только один острый угол.
Две параллельные прямые — свойства и признаки
Если в задаче есть параллельные прямые — это большая удача, ведь они дают много равных углов, с помощью которых можно вычислить практически все, что угодно. Сейчас мы разберемся, какие еще бонусы дает установление параллельности, и чем это может быть полезно при решении задач.
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей.
В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
- два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠5 = 180°; ∠3 + ∠6 = 180°.
- два внутренних накрест лежащих угла равны между собой:
∠3 = ∠5, ∠4 = ∠6.
- два соответственных угла равны между собой:
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых.
Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
В данном случае ∠3 и ∠MPK являются вертикальными, следовательно ∠MPK = ∠3 = 92°.
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
∠4 = 180° — 92° = 88°
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см.
Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку
а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
DK = 2DM = 2 х 27 = 54 (см)
Шпаргалки по математике родителей
Все формулы по математике под рукой
Углы в параллельных линиях — GCSE Maths
Введение
Что такое углы параллельных прямых?
Ключевые факты об углах
Как найти недостающий угол в параллельных прямых
Углы в параллельных линиях рабочий лист
Распространенные заблуждения
Практика углов в параллельных линиях вопросы
Углы в параллельных линиях Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое углы параллельных прямых?
Ключевые факты об углах
Как найти недостающий угол в параллельных прямых
Углы в параллельных линиях рабочий лист
Распространенные заблуждения
Практика углов в параллельных линиях вопросы
Углы в параллельных линиях Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о углах в параллельных линиях , в том числе о том, как распознавать углы в параллельных линиях, использовать факты об углах для нахождения отсутствующих углов в параллельных линиях и применять факты об углах в параллельных линиях для решения алгебраических задач.
Есть также рабочие листы с углами в параллельных линиях, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Что такое углы параллельных прямых?
Углы в параллельных прямых — это углы, которые образуются при пересечении двух параллельных прямых другой линией, называемой секущей .
Мы можем использовать информацию, приведенную на диаграмме, чтобы найти любой угол вокруг пересекающейся секущей.
Для этого воспользуемся тремя фактами об углах параллельных прямых:
Альтернативные углы , со-Внутренние углы, и соответствующие углы.
Свойства параллельных линий
- Альтернативные углы равны :
Иногда их называют «Z-углами».
- Соответствующие углы равны :
Иногда их называют F-угламиo)
Вертикально противоположные углы
(вертикально противоположные углы — это тот же размер
)
Углы в параллельных строках
Мы знаем, что верные внутри наших параллельных линий:
Если мы продлим поперечную линию так, чтобы она пересекала большее количество параллельных линий, полученные углы сохранятся на всей диаграмме для любой линии, параллельной исходной линии AB.
Верхний наконечник : для одной и той же пересекающейся поперечной все острые углы имеют размер , а все тупые углы имеют размер .
Мы группируем эти углы в три отдельных типа, называемых альтернативными углами , совмещенными внутренними углами и соответствующими углами .
Альтернативные углы
Альтернативные углы — это углы, которые возникают на противоположных сторонах поперечной линии и имеют того же размера .
Каждая пара альтернативных углов вокруг поперечной равна друг другу.
Два угла могут быть чередующимися внутренними или внешними углами.
Другие примеры альтернативных углов:
Мы часто можем определить внутренние альтернативные углы, нарисовав форму Z:
Пошаговое руководство: Альтернативные углы
Соответствующие углы
Пары углов, образованные на одном и том же стороны поперечной, которые либо обе тупые, либо обе острые и называются соответствуют углам и равны по размеру.
Каждая пара из соответствующих углов на одной стороне пересекающейся секущей равна друг другу.
Другие примеры соответствующих углов:
Внутренние соответствующие углы часто можно определить, нарисовав форму F:
Пошаговое руководство: Соответствующие углы
Со-внутренние углы
2 90 углы по одну сторону от пересекающейся секущей в сумме дают 9о
Другие примеры кооттедвированных углов:
I+J = 180 O
K+L = 180 O
M+N = 180
. часто определяют внутренние совмещенные углы, рисуя форму буквы C.
Пошаговая инструкция: Внутренние углы
Как найти недостающий угол в параллельных прямых
Чтобы найти недостающий угол в параллельных прямых:
1 Выделите углы, которые вы уже знаете.
2 Укажите альтернативный угол, внутренний угол или факт соответствующего угла, чтобы найти недостающий угол на диаграмме.
3 Используйте базовые данные об углах для расчета недостающего угла.
Шаги 2 и 3 можно выполнять в любом порядке, и их может потребоваться повторить.
Шаг 3 может потребоваться не всегда.
Как найти недостающий угол в параллельных прямых
Рабочий лист углов параллельных линий
Получите свободный рабочий лист углов параллельных линий, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Икс
Рабочий лист углов параллельных линий
Получите свободный рабочий лист углов параллельных линий, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Углы параллельных прямых примеры
Для каждого этапа расчета мы должны четко указывать любые используемые нами факты об углах.
o
. 9o
Распространенные заблуждения
- Перепутывание фактов об углах
Существует множество фактов об углах, и альтернативные углы легко перепутать с соответствующими углами. Чтобы этого не произошло, представьте, что альтернативные углы находятся на противоположных сторонах линии.
- Использование транспортира для измерения угла.
Большинство диаграмм не в масштабе, поэтому использование транспортира не приведет к правильному ответу, если только это не совпадение. 9{circ}
Углы в параллельных прямых вопросы GCSE
1. (a) Ниже приведена диаграмма, показывающая две параллельные прямые, пересекаемые секущей:
Напишите уравнение, соединяющее 2 r 5 s и
(b) Учитывая, что отношение углов r : s равно 3 : 5 , напишите другое уравнение, связывающее r и s.
(2 балла)
Показать ответ 9{circ}
(1)
Учебный контрольный список
Теперь вы научились:
- применять свойства углов в точке, углов в точке на прямой, вертикально противоположных углов
- понимать и использовать отношения между параллельными линиями и альтернативными и соответствующими углами
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Параллельные прямые и пары углов
Параллельные прямые и пары углов
Показать рекламу
Скрыть рекламу
О рекламе
Параллельные линии
Линии параллельны, если они всегда находятся на одном и том же расстоянии друг от друга (называемом «эквидистантными») и никогда не пересекутся. Просто помните:
Всегда на одинаковом расстоянии друг от друга и никогда не касаясь
.
Красная линия параллельна синей линии в каждом из следующих примеров:
Параллельные линии также указывают в одном направлении.
У параллельных линий так много общего.
Жаль, что они никогда не встретятся!
Попробуйте сами:
Пары углов
Когда параллельные прямые пересекаются другой прямой (называемой секущей), вы видите, что многие углы совпадают, как в этом примере:
Эти углы можно составить из пар углов , которые имеют специальные имена.
Нажмите на каждое имя, чтобы выделить его:
Теперь поиграйте с ним здесь. Попробуйте перетаскивать точки и выбирать различные типы углов. Вы также можете включить или выключить «Параллельность»:
Проверка параллельных линий
Некоторые из этих специальных пар углов можно использовать для проверки параллельности прямых:
Пусть а— прямая, М- точка, не лежащая
наа. Опустим перпендикуляр наа:MNa.
Обозначим прямуюа: АВ, так, чтобы
А-N-В.!EF//BAи!
СD//АВ
Утверждение 1FMN=DMN.
Доказательство: Ясно, чтоEFи СDразличные прямые т.
к. эти углы меньше прямого. Это следует
из док–ва теоремы, что точка, производящая
сечение, лежит междуNи
Р. Доказательство легко проводится от
противного: ПустьDMN>FMN.
Рассмотрим луч МF/симметричный МFотносительно
МN, т.е. отложим в другой
полуплоскости угол, равныйFMN,
т.к.DMN>FMN,
то МF/— внутренний
луч углаDМN.
А т.к. СD//АВ, тоMF/NB,
но симметрия — это биекцияи
МFВА.
Противоречие.
Опр. 2.Каждый из острых углов,
образованных прямыми // прямой а, с
перпендикуляром опущенными из их общей
точки называется углом параллельности
в т. М относительно прямой а.
Утверждение 2.Мера угла
параллельности вполне определяется
расстоянием от точки М до прямой а (не
зависит от выбора т. М и прямой а).
Доказательство 
Пусть NMD-угол
параллельности в т. М относительноа.N/M/D/угол параллельности в т. М/относительноа/. Докажем, что
еслиx=x/,
то/ =.
Пусть />.лучh/-внутренний
для углаN/M/D/и такой, чтоN/M/F/=,
гдеh/a/=F/.
Нааот т.Nотложим
т.F, так чтобыFиDлежали в одной
полуплоскости иNF=N/F/,
но тогдаNF=N/F/МNF=М/N/F/NМF=MFи МDсовпадают, а значит
МDиапересекаются.
Противоречие. Ч.т.д.
Значит, мера угла параллельности есть
функцияот х:
Обозначается =(х)-
она называется функцией Лобачевского.
Ясно, что (из Тh2)(х)
определена для любого х0
и, кроме того, 0(х)
,k- некоторое положительное
число.
(х)- монотонно убывающая функция и
непрерывная, а значит, принимает все
значения из (0,
).
Это означает, что любой острый угол
является углом параллельности в некоторой
точке относительно данной прямой.
Существование такой функций говорит о
том, что между угловыми и линейными
величинами имеется зависимость, т.е. —
за единицу длины можно выбрать отрезок,
которому соответствует угол параллельности,
равный, например,
.
§3. Треугольники и четырехугольники на плоскости Лобачевского
В этом § будут изложены некоторые факты,
отличные от тех которые мы имеем в
Евклидовой геометрии (сказать, что
высоты не обязательно в одной точке).
Теорема 1.Сумма углов любого
треугольника меньше 2d
(т.е. меньше двух прямых).
Доказательство.ПоTh1
Саккери — ЛежандраАВС2d,
но если она =2d, то имеет
местоVпостулат по Тh2
(противоречие) ч.т.д.
Следствие.Сумма углов треугольника
непостоянна.
Пусть АВС — произвольный треугольник.
Dстороне
АС.АВС=АВД+BCD
— 2d=АДСABC<ABD.
Следствие 2.Сумма углов выпуклого
четырехугольника меньше 4d.(очевидно).
Теорема 2. (четвертый признак
равенства треугольников)Если три
угла одного треугольника соответственно
равны трем углам другого треугольника,
то эти треугольники равны.
Доказательство:Пусть вАВС
иА/В/С/А=А/,В=В/,С=С/.
Достаточно доказать, что АВ=А/В/,
а затем применитьпризнак равенства треугольников. Пусть
АВА/В/,
например, АВА/В/.
На лучах АВ и АС возьмем т. В//и
С//, так чтобы АВ//=А/В/,
АС//=А/С/.АВ//С/=А/В/С/В//=В/=В,С//=С/=С.
В//лежит между А и В. Надо доказать,
что С//лежит между А и С, ноВ=В//прямая
В/С//не пересекает ВСпо аксиоме Паша она пересекает АС, т.е.
А-С//-С. Четырехугольник В//С//СВ
лежит по одну сторону от каждой прямой,
содержащей его сторонуон
выпуклый и егоВ//С//СВ=4d,
что противоречитследствию2 .
Следовательно В//совпадает с
В.
Опр. 1 Двупрямоугольником
называется выпуклый четырехугольник,
у которого два угла, прилежащие к одной
стороне, прямые.
П
устьABCD– двупрямоугольник.А иВ
прямые. Тогда сторона АВ называетсяоснованием, аADиBC–боковыми сторонами.
Опр. 2 Двупрямоугольник с
равными боковыми сторонами называется
четырехугольником Саккери.
Свойство 1. Если АВСDчетырехугольник Саккери с основанием
АВ, тоС=Dи оба они острые.
Доказательство. Рассмотрим симметрию
с осьюd. При этомSd(АD)=BС
(BD/=BC)D=С2d.
Свойства 2. Если в двупрямоугольнике
с основанием АВ, АD<ВС,
тоС<D.
Легко.
Свойство 3. Если в двупрямоугольнике
с основанием АВ,С<D,
то АD<ВС. Самостоятельно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #