УЧЕТ ПРОЙДЕННОГО РАССТОЯНИЯ И СКОРОСТИ СУДНА
Для того чтобы точно и в заданный срок провести судно из одной точки в другую, судоводителю надо знать истинный курс судна, его скорость и время лежания на курсе.
Расстояние, проходимое судном, можно рассчитать по формуле, Скорость судна выражается количеством миль в час.
Значение скорости, равное одной миле в час, имеет свое наименование — узел. Этот термин сохранился еще со времен парусного флота. (Лаг—прибор для определения пройденного расстояния — представлял собой в те времена линь, ходовой конец которого крепился к сектору-поплавку, выбрасываемому в воду, а коренной находился в руках наблюдателя. Линь был размечен узелками через 1/120 часть морской мили и по ходу судна свободно выпускался за корму. Наблюдатель в течение 0,5 мин отсчитывал, сколько узелков уйдет за борт, и по их числу определял скорость судна. Название «узел» прижилось и сохранилось до нашего времени.)
Обычно скорость судна определяют между двумя точками, которые точно известны. Расстояние снимают с карты. Тогда скорость, уз,
V=S60/t
где S — расстояние с карты, мили;
t — время лежания на курсе, мин.
Скорость рассчитывают до десятых долей узла.
Пройденное расстояние по курсу
S=Vt/60
Однако надо учитывать, что при разных условиях плавания путевая скорость будет иметь разные значения. Более точно пройденное судном расстояние показывает лаг.
Лаги в зависимости от принципа действия и устройства подразделяются на вертушечные, гидродинамические и индукционные.
На судах речного флота в настоящее время применяются гидродинамические и индукционные лаги. В вопросах навигации следует учитывать, что гидродинамические лаги показывают пройденное расстояние относительно воды и течение не учитывают.
Каждый лаг, не являясь абсолютно точным прибором, имеет свою поправку. Обычно для определения поправки лага используют мерную линию.
Поправка лага, %,
ΔЛ = (S-РОЛ)/РОЛ * 100
где РОЛ—разность отсчетов лага, т. е. РОЛ=ОЛ2—ОЛ1.
Пройденное судном расстояние относительно воды с учетом поправки лага
Sл = РОЛ+РОЛ(ΔЛ/100)
или
Sл = РОЛ(1+(ΔЛ/100)
По данным формулам составлены таблицы в МТ—75 для положительных и отрицательных поправок лага. Для входа в таблицы надо знать разность отсчетов лага и поправку лага.
Коэффициент лага используется часто вместо поправки лага.
Коэффициент лага
Кл=S/РОЛ
Этот коэффициент рассчитывают с погрешностью до 0,01.
Между Кл и ΔЛ существует следующая зависимость:
ΔЛ=(S/РОЛ –1)100
Но S/РОЛ=Кл. Следовательно, ΔЛ=(Кл—1)100, откуда Кл=1 + ΔЛ/100
ГРАФИЧЕСКОЕ И АНАЛИТИЧЕСКОЕ СЧИСЛЕНИЕ ПУТИ СУДНА
Важнейшее условие решения задач судовождения и обеспечения безопасности плавания — непрерывное и тщательное нанесение на карту пути перемещения судна, чтобы в любой момент знать место судна и иметь возможность ориентироваться по карте в навигационной обстановке, окружающей судно. Это достигается ведением счисления пути судна.
Счисление — это учет перемещения судна с целью знания его места в любой заданный момент. Счисление ведется по элементам движения судна — по курсу, скорости и времени. Оно должно быть непрерывным, наглядным, точным и обеспечивать быстроту получения места.
На перемещение судна в море могут влиять ветер, создающий дрейф судна, и течения, вызывающие снос.
Счисление может быть графическим и аналитическим. При графическом счислении с помощью прокладочного инструмента на карту наносят истинный курс судна, и по нему откладывают пройденное судном расстояние. Кроме этого, делают и другие построения, позволяющие учесть влияние на перемещение судна ветра и течения.
При аналитическом (письменном) счислении рассчитывают координаты судна на определенный момент по специальным формулам.
Графическое счисление является основным, так как оно наиболее полно удовлетворяет требованиям, предъявляемым к счислению. Недостатком его является зависимость точности счисления от масштаба карты, на которой оно ведется.
Недостаток аналитического счисления—отсутствие непрерывности и наглядности.
Место судна, рассчитанное с помощью счисления, называется счислимым местом.
Для получения счислимого места судна необходимо знать истинный курс и пройденное расстояние.
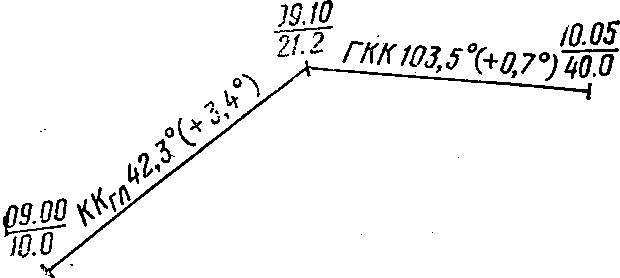
Графическое счисление выполняют следующим образом. На морской навигационной карте по соответствующим координатам наносится точка, из которой прокладывается истинный курс. У начальной точки записываются время и отсчет лага — Т1 и ОЛ1 Чтобы найти место судна в последующий момент Т2 при отсчете лага ОЛ2, надлежит по линии истинного курса от исходной точки отложить расстояние, пройденное судном за время Т2—Т1. Пройденное расстояние рассчитывается с точностью до 0,1 мили.
Рис. 34. Графическое счисление
Расстояние по лагу
Sл= Kл(ОЛ2-ОЛ1).
Счислимое место судна на карте обозначают небольшой черточкой, пересекающей линию курса. Вблизи ее пишется дробью момент по часам и отсчет лага.
Дробную черту проводят горизонтально с помощью линейки. Вдоль линии курса записывают значение компасного курса с учетом поправки компаса, которую указывают в скобках (рис. 34).
Абсолютный лаг измеряет две составляющие
абсолютной скорости VхиVу.
Указатели лага
абсолютной скорости показывают все
четыре элемента:
Скорость вдоль
ДП судна — Vx, скорость поперечную -Vy,
скорость абсолютную –Vи угол сноса –С.
C
Рис. 1.23
V =
,tgC=
,
где С – суммарный угол сноса.
5.4 Учет поправки лага при счислении
Лаги,
измерители скорости и пройденного
расстояния, как и другие навигационные
приборы, имеют поправки, которые
необходимо учитывать при расчетах.
Поправка
лага определяется на специальном
полигоне, называемом «мерной линией»,
и учитывается при расчетах пройденного
расстояния следующим образом:
(1.37)
SЛ= РОЛ(1+).
КЛ= 1 +(1.38)
SЛ= КлРОЛ (1.39)
РОЛ =
(1.40)
РОЛ = ОЛ2– ОЛ1
S–
расстояние между створами на мерной
линии,
SЛ– пройденное расстояние относительно
воды за определенный промежуток времени,
РОЛ – разность отсчетов
лага,
ОЛ1– отсчет
лага в начальный момент,
ОЛ2– отсчет
лага в конечный момент,
Л– поправка
лага в процентах, бывает положительной
и отрицательной,
КЛ–
коэффициент лага.
Пример 1.Измерили относительную скорость судна
и поправку лага по морскому бую. При
следовании на буй в начальный момент
Т1=0 сек секундомера,
показание лага ОЛ1 = 56,33, и
дистанция до буя D1
= 2,8. В дистанции до буя D2
= 1,5 мили остановили секундомер
Т2
=390 сек, и сняли отсчет лага ОЛ2
= 57,67. Рассчитать V0
и Л%..
Решение:VЛ
=узлов
Л%
=
Пример 2.На мерной линии длиной 3 мили
предполагается наличие течения,
совпадающего с направлением ведущего
створа 70-250.
Для определения скорости судна о поправки
лага судно сделало два пробега. На ИК
= 250 время
по секундомеру Т = 1740 сек и РОЛ1
= 3,6. На ИК = 70
Т = 1080 сек, а РОЛ = 2,3. Рассчитать скорость
судна относительно воды VЛ
и поправку лага Л%.
Решение.
Рассчитаем скорости судна на каждом
галсе.V1=
узла
V2=
узлов.
Тогда скорость относительно воды
будет:
VЛ=
узла. Теперь рассчитаем пройденное по
лагу расстояние на обоих галсах.
SЛ=
мили и пройденное расстояние по показаниям
лага: РОЛ = 3,6+2,3=5,9
Отсюда
коэффициент лага КЛ=,
поправка лагаЛ%= 100 (1,07 – 1) =+ 7%.
Пример 3.Расстояние между обсервациями, снятое
с карты равно SЛ
= 22 мили, а разность отсчетов лага РОЛ =
20,0. Определить поправку лага.
Решение.
КЛ=.
Отсюда находим поправку лагаЛ%= 100(1,1 – 1) = + 10%
Контрольные вопросы
-
Морские единицы
скорости судна. -
Как рассчитывается
коэффициент лага КЛ? -
Определение
поправки лага с помощью свободно
плавающего ориентира.
Глава 6
Счисление
пути судна
6.1 Графическое счисление пути судна
Счисление координат
судна (счислением) называется вычисление
текущих координат судна от известных
координат по времени, курсу и скорости
с учетом влияния на судно ветра и течения.
Графическое счисление выполняется
непосредственно на морской навигационной
карте с использованием штурманских
прокладочных инструментов (параллельной
линейки, транспортира и циркуля
измерителя) и называется графическим
счислением или навигационной прокладкой.Навигационная прокладка это графическое
изображение на морской карте пройденного
судном маршрута (или части его),
выполненное автоматически или вручную
на основе измерений и вычислений.Если счисление выполняется по формулам
и таблицам, оно называется аналитическим
(письменным). Прокладка может быть
предварительной и исполнительной.Предварительной прокладкой называется
навигационная прокладка маршрута судна,
выполненная предварительно, исходя из
намеченного маршрута, отвечающего
требованиям плавания, поставленным
задачам и экономической целесообразности.
При выборе пути судна руководствуются
двумя условиями:
-
безопасность
плавания, -
экономичность
перехода (как правило, это наименьшая
затрата времени).
Выбранный маршрут
наносится на навигационные генеральные
карты с указанием курсов, длительности
пути на курсе и точек поворота или
ориентиров в точках поворота. Дальнейшая
задача судоводителя сводится к обеспечению
движения судна по намеченному пути и
контролю за этим движением (исполнительная
прокладка).Навигационная прокладка
начинается с момента выхода судна с
акватории порта и заканчивается в момент
прихода судна в порт (от причала до
причала). Основным методом непрерывного
учета положения судна является графическое
счисление. Оно заключается в систематическом
нанесении положения судна на карту по
данным о его движении и пройденного
расстояния, а также сведениям о течении
и дрейфе. Начальная точка счисления
должна быть известна. Место судна,
координаты которого получены по
счислению, называются счислимыми.
Контроль прокладки
производится путем измерения различных
навигационных параметров (пеленгов,
расстояний, разности расстояний и высот
светил) и получения места судна путем
обсервации по двум, трем и более линиям
положения.
Геометрические
величины, измеряемые непосредственно
или же получаемые косвенным путем для
определения места судна в море по
береговым и небесным светилам называются
навигационными параметрами.
Геометрическое место
точек, отвечающих постоянному значению
величины, измеренной для обсервации
(навигационного параметра) называется
изолинией. Изолиния в общем случае
является кривой линией. Для обсервации
необходимо иметь лишь небольшие отрезки
изолиний в точке пересечения их под
углом друг к другу. Отрезки изолиний
без особой погрешности можно заменить
отрезками прямых, касательных к изолинии
или их секущими. Касательная или
секущая к изолинии называется линией
положения. Изолиниями могут быть
пеленг, изостадия (окружность), изогона
(окружность), гипербола.
Все графические работы,
выполняемые на карте, состоят из отдельных
элементов задачи. К таким задачам относят
снятие с карты координат судна или
нанесения места судна на карту, расчет
и прокладка курсов и пеленгов, измерение
расстояний между определенными точками.
При ведении прокладки решаются задачи
двух типов: прямая и обратная.
Первая (прямая)
задача предусматривает только учет
движения судна, когда курс рулевому
задан.
ИК = КК + к.
Рассчитывают истинный
курс и прокладывают на карте линию
курса в виде прямой от исходной точки.
При отсутствии сноса от течения и ветра
(дрейфа) линия истинного курса будет
совпадать с путевым углом, следовательно,
судно будет перемещаться по проложенному
на карте курсу. На карте у точки, принятой
за исходную для ведения счисления,
надписывается время с точностью до 1
минуты и отсчет лага с точностью до 0,1
мили ().
Дальнейшее нанесение положения судна
на любой момент времени производится
по расстоянию, пройденному судном по
лагу от исходной точки. Положение судна
на линии проложенного курса отмечается
каждый час при плавании вблизи берегов
и каждую вахту – при плавании в открытом
море, а также при любом изменении курса
или скорости. Каждую счислимую точку
обозначают чертой длиной около 5 мм,
перпендикулярной предшествующему
курсу. Каждую обсервованную точку
отмечают специальным знаком, присвоенным
данному виду обсервации.
В практике судовождения
обратная задача встречается гораздо
чаще и состоит в том, что судну необходимо
следовать заданным ИК. В этом случае
рулевому задается предварительно
рассчитанный КК, исходя из проложенного
ИК.
КК = ИК — к.
Если необходимо
рассчитать отсчет лага на момент прихода
в заданную точку, то предварительно
снимают с карты S–
расстояние, которое необходимо пройти
от исходной точки до точки поворота.
Далее рассчитывают РОЛ и затем ОЛ2.

и ОЛ2= ОЛ1+ РОЛ
Время прихода в
расчетную точку рассчитывают:
T2=T1+T=T2+
Вдоль линии курса
надписывается компасный курс судна, в
скобках — поправка компаса.

+
+
47
0400Е
0420
Рис. 1.24
Прямая задача
Обратная задача

ИК – снят с карты
+
— из таблицы девиации по КК -()d
– с карты
МК
– магнитный курс МК – магнитный
курс
+
– склонение с карты -()
— из табл. девиации по МК
ИК
КК
При прямой задаче
выбранные склонение и девиация со своим
знаком складываются с КК и МК, а при
обратной задаче – вычитаются из ИК и
МК.
Учет дрейфа и
постоянного течения при прокладке.
Дрейфом судна
называется смещение движущегося судна
с линии истинного курса под воздействием
ветра.Дрейф судна создается кажущимся
ветром. Направлением ветра называют то
направление, откуда он дует (говорят:
ветер дует в компас). Если ветер дует в
левый борт судна, то говорят судно идет
левым галсом (л/г или л/б), по отношению
к ветру.
Если ветер дует в
правый борт, то судно идет правым галсом
(пр/г или пр/б). Направление равнодействующей
сил давления ветра (Р) в общем случае
не совпадает с направлением вектора
скорости кажущегося ветра (W).
Величина
угла дрейфа зависит от многих факторов:
осадки, размеров и формы надводной и
подводной частей корпуса судна, курсового
угла и скорости кажущегося ветра,
скорости хода судна. Для учета дрейфа
при прокладке необходимо знать угол
дрейфа. Имеется ряд способов его
определения, но все они не являются
точными, что приводит иногда к значительному
отклонению от намеченного на карте
пути.
Разложим эту силу (Р)
на две составляющие: продольную (Р1)
и поперечную (Р2).
(+), а при ветре правого
галса знак при угле дрейфа будет (-).
ПУ=- ИК +. ИК = ПУ-. (1.41)
При учете дрейфа на
карте прокладывают только линию путевого
угла дрейфа. Так как лаг учитывает
влияние ветра на скорость судна (Р1),
то и расстояние можно учитывать,
откладывая по линии пути (Sл
= РОЛ Кл).
Nи
ИК
ПУ
В
А
Р1
Р2
Р
Рис. 1.25
Расчеты по прямой и
обратной задачам удлиняются по сравнению
с расчетами без влияния ветра.
Поперечная составляющая Р2вызывает дрейф судна. Поэтому при ветре
судно перемещается относительно воды
не вдоль диаметральной плоскости, а под
некоторым углом к ней (),
называемым углом дрейфа. Линия АВ, по
которой перемещается судно, называется
линией пути при дрейфе, а угол ПУ,
который она составляет с истинным
меридианом, называется путевым углом
дрейфа. При ветре левого галса углу
дрейфаприсваивается
знак (+) плюс, при ветре правого галса –
знак (-) минус.
КК =
ПУ= с карты
+()
= из таблицы-()
= принят для счисления
МК =
ИК =
+()d
= с карты—()d
= с карты
ИК =
МК =
+()= принят для счисления
-()= с карты

КК =
Nи
ПУ
В
Т
Vт
ИК
Vл
Vт
Рис.1.26
C
А
V
Поступательное
движение водной массы в морях и океанах
называется течением. Элементами течения
являются его скорость и направление.
Направление течения определяется
мнемоническим правилом: «течение идет
из компаса». Направление течения
показывают в градусах, а иногда в румбах,
скорость выражается в узлах.
Под
действие упора движителя, судно получает
движение относительно воды по направлению
диаметральной плоскости (Vл).
Если вода имеет движение
относительно Земли, то скорость судна
относительно Земли определится
геометрической суммой скоростей:
И судно будет перемещаться
по направлению вектора
,
если скорость суднаи течения
постоянны по величине и направлению,
суммарная скоростьтакже будет неизменна и судно пойдет
по прямой АС.
N
В
Vm
VЛ
Рис. 1.27
Угол
ПУ между северной частью истинного
меридиана и направлением движения судна
называется путевым углом
(путем), а линия пути АС будет линией
пути на течении. Угол
между линиями истинного курса (ИК) и
путевым углом (ПУ) называется углом
сноса от течения.
Скорость Vбудет истинной скоростью судна
(относительно дна).
ПУ = ИК + ()ИК = ПУ – ().
(1.42)
Знак у зависит от направления сноса. Если
течение направлено в левый борт, то знак
у(+), а если в правый
борт, то знак у(-).
Учет течения
сводится к решению треугольников
(скоростного и путевого).
Вначале графически
складывают векторы скоростей судна и
течения, а затем решают путевой
треугольник АВС.
Различают
прямую и обратную задачи графического
решения треугольника скоростей. Прямая
задача.
В прямой задаче
по заданным ИК, Vл, Кт иVт
требуется рассчитать угол,
ПУ иV(Рис.1.27). Для
получения линии пути ПУ из точки А
проводим линию ИК и на ней от точки А
откладываем отрезок, равный вектору
скорости судна по лагу (VЛ)
в условном масштабе. Обычно берется
количество миль в масштабе карты,
проходимое судном за час или полчаса.
Из конца вектора скорости судна (VЛ)
проводим вектор скорости течения (VТ)
в том же масштабе. Соединив точку А с
концом вектора скорости течения (Vт),
получим
линию пути судна
(ПУ).Снимаем с карты направление этого
пути для сравнения с истинным
курсом (ИК) и получения
угла сноса от течения ().
= ПУ – ИК.
(1.43)
Для
получения счислимой точки за любой
временной промежуток плавания по
путевому углу, необходимо по линии
истинного курса (ИК) отложить пройденное
по лагу расстояние (Sл =
РОЛ Кл). Полученную на ИК точку сносим
по линии направления течения на линию
путевого угла (ПУ) (точки В и С). Надписи
на карте производятся над или под линией
пути (ПУ) и параллельно ей. Порядок записи
таков: пишется ГКК рядом в скобках его
поправка, а затем величина сноса от
течения со своим знаком(ГКК 69
(-2)
= +6).

=
+()
= из таблицы девиации

+()d
= с карты


= из построения
ПУ
=
Обратная задача
В этой задаче
необходимо по заданному ПУ,
Vл, Кт и Vт
рассчитать угол сноса течением ()
и ИК (Рис.1.28).
Задача решается
следующим образом:
Пусть на карте
проложена линия ПУ (АК). Из точки А
прокладываем вектор скорости течения
VT,
выраженный количеством миль. Из конца
вектора скорости теченияVTраствором циркуля, равным скорости
суднаVЛ, делаем на
линии ПУ судна засечку (точка С). Соединив
точку С с концом вектора скорости течения
переносим ее параллельно в начальную
точку А, проведя линию истинного курса
АD.
Нахождение счислимой
точки при уже построенном треугольнике
скоростей, производится так же, как и в
прямой задаче. По расстоянию Sл
находим на линии ИК точку В, и затем
через точку В проводим линию, параллельную
вектору скорости теченияVт.
Пересечение этой линии с линией ПУ и
будет счислимым местом судна (точка С).
Кроме графического
учета течения существует и аналитический,
который применяется при автоматизации
судовождения.


К

С

Vт
Т
Рис.1.28

= направление, снятое с карты

ИК
=
-()d
= с карты
МК
=
-()= из таблицы девиации по МК

Совместны учет
дрейфа течения
При одновременном
действии ветра и течения судно будет
подвергаться как дрейфу, так и сносу
течением. Угол, на который линия пути
отклонится от линии истинного курса
(ИК), называется суммарным углом сноса
(С).
С= ПУ – ИК
(1.44)
Знак угла суммарного
сноса (С) получается из приведенной
формулы: если ПУ ИК,
то знак будет плюс (+), если ПУИК, то знак будет минус (-). Если же известны
величины угла дрейфа ()
и угла сноса течением (),
то знак суммарного сноса определится
из алгебраического их сложения. С=+(1.45)
При наличии ветра и
течения решаются также прямая и обратная
задачи, как и при наличии только течения.
При решении прямой задачи сначала
учитывают дрейф и на карту наносят линию
пути ПУ. Затем
учитывают течение, строя треугольник
скоростей, причем скорость судна
откладывается по линии путевого угла
дрейфа (ПУ), а не по
линии ИК.
В обратной задаче при
заданном ПУ решают треугольник скоростей,
при этом из построения получают не
направление ИК, а направление ПУ.
Затем снимают направление пути дрейфа
(ПУ) и находят
истинный курс: ИК = ПУ-, а также
= ПУ — ПУи С=+.
На карте под (или над)
линией путевого угла делается запись
о компасном курсе, его поправке и о
суммарном угле сноса (ГКК (-2) С= -12)
В общем виде решение
задачи выглядит таким образом:
Прямая
задача
Обратная задача

=
ПУ =
+()
= из таблицы девиации—)
= из построения
МК =
ПУ=
+()d
= с карты-()
= принятый
ИК =
ИК =
+()= принятый для счисления
— ()d= с карты

МК =
+()
=-()
= из таблицы
дв.
ПУ =
КК =
Пример 1.В широте
= 5300
Nсудно следует
ИК = 75,0 со
скоростью 12 узлов. Учитывается течение
335 – 1,1 узла.
Определить угол сноса судна течением
.
Решение: От
исходной точки, от которой проложен ИК
= 75,0. Откладываем
расстояние, пройденное судном за один
час (скорость судна)SЛ.
От
полученной точки на ИК откладываем по
направлению течения снос судна течением
за один час (скорость течения) SТ= 1,1 мили.
Соединяем
исходную точку с полученной на векторе
течения и с помощью параллельной линейки
и транспортира снимаем отсчет ПУ = 69,0.
Рассчитываем
угол сноса течением .
ПУ = 69,0
— ИК = 75,0
= — 6,0
Пример 2.В широте
= 5300
Nсудно следует,
имея скорость по лагу 12 узлов.На
карте от исходной точки проложен ПУ =
52,8. На судне
учитывается течение 143
– 1,0 узел. Определить ИК и .
Решение: Из
исходной точки проводим линию направления
течения и на ней откладываем отрезок,
равный скорости течениеVT=1.0
узл.
Из полученной точки
радиусом, равным скорости судна 12 узлов,
на линии ПУ делаем засечку и соединяем
обе точки прямой.
С помощью параллельной
линейки транспортира снимаем значение
ИК = 48,8
Рассчитываем угол
сноса течением .
ПУ = 52,8
— ИК = 48,0
= + 4,8
Пример 3.Дано:
ПУ = 356,6,
= — 6,2,
= + 4,0, ГКК
= -1,2. Определить
ГКК.
Решение:
ПУ = 356,6
—
= — 6,2
ПУ= 002,8
—
= +4,0
ИК = 358,8
— ГКК
= -1,2
ГКК = 360,0
Пример 4.Рассчитать
радиальную СКП счисления без учета
влияния ветра и течения, если судно
прошло 100 миль.
Решение: Из
НШСР -86 (таблица № 3) выбираемmK= 0,7,mЛ%= 0,5%, тогда
b= 0,0174
* 0,7 * 100 = 1,218
a= 0,01 *
0,5 * 100 = 0,5
M=b2+a2=1,48
+ 0,25 = 1, 3 мили.
Контрольные вопросы
-
Какой знак (+) или
(-) присваивается углу дрейфа правого
борта? -
Направление
течения считается в «компас или из
компаса»? -
Как рассчитать
общий снос от ветра и течения при
известных ПУ, ПУ,
ИК? -
Какая приближенная
зависимость СКП графического счисления
от пройденного расстояния? -
С чего начинают
решение обратной навигационной задачи
при учете течения?
Тема, рассматриваемая в видеоролике – это определение времени и отсчёта лага при кратчайшем расстоянии до ориентира при учете ветра и течения. Преподаватель доступно и кратко разъяснит методику решения такой задачи и проиллюстрирует свои вычисления для большей доступности и понимания.
Сноски
-
Просмотров: 42221
Единицы длины и скорости в навигации
Основной единицей длины в навигации является морская миля. Морская миля — длина одной минуты дуги меридиана эллипсоида: ∆1’m = M * arc 1′ = 1852,3 — 9,3 * cos2φ; М — радиус кривизны меридиана эллипсоида.
Таким образом, морская миля — величина переменная, которая зависит от широты места и составляет I843 метра на экваторе и 1861,6 метра на полюсе. Использовать в качестве единицы длины переменную величину крайне неудобно.
В 1931 году в качестве единицы длины была принята стандартная миля, равная длине одной минуты дуги меридиана эллипсоида в широте 44° 18′ и составляющая 1852 метра. Отклонение длины стандартной мили не превышает 0,5% от экстремальных значений длины одной минуты дуги меридиана на экваторе и полюсе и находится в пределах точности корабельных измерителей скорости и пройденного расстояния.
В настоящее время термин стандартная миля практически вышел из употребления и заменен термином — морская миля. Кабельтов — одна десятая часть морской мили = 185,2 метра.
Основной единицей скорости в навигации является узел — скорость, равная одной морской миле в час.
При решении некоторых задач кораблевождения применяется единица скорости — 1 кабельтов в минуту. Для перехода от скорости в узлах к скорости и каб/мин используется соотношение:
Скорость в узлах / 6 = скорость в каб/мин.
Например, если скорость корабля 18 узлов, то он проходит 18 морских миль в час или 18/6 = 3 кабельтова в минуту.
Скорость корабля
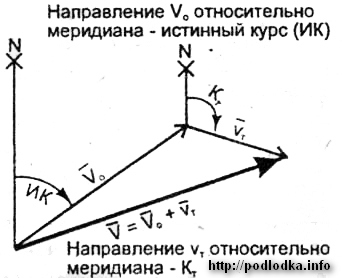
Скорость корабля относительно поверхности воды под воздействием движителей и ветра — относительная скорость (V0). Под воздействием течения корабль вместе с водными массами перемещается относительно морского дна со скоростью течения (Vт). Таким образом, под воздействием собственных движителей, ветра и течения корабль перемешается относительно морского дна со скоростью V, которая называется абсолютной или путевой.
Направление вектора абсолютной или путевой скорости корабля V относительно меридиана — путь корабля — линия его фактического перемещения.
Измерители скорости на корабле
Лаг — прибор для измерения скорости на корабле:
— относительный — измеряет V0;
— абсолютный — измеряет V.
По физическим принципам измерения относительной скорости лаги подразделяются на:
— гидродинамические: Рп = f (V0), Рп — полное давление набегающего потока волы;
— индукционные: Е = f (V0), Е — э.д.с, образующаяся в проводнике, при его перемещении в магнитном поле.
Конструктивно относительные лаги выполнены в виде двух основных блоков:
— измерения скорости V0;
— вычисления пройденного кораблем расстояния So (счетчик пройденного расстояния)
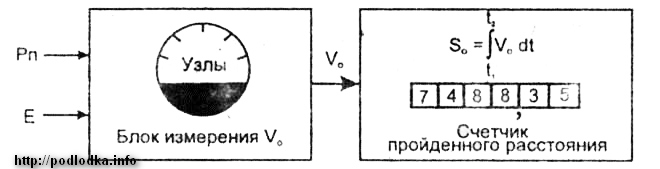
Скорость, снимаемая с приборов относительного лага — Vл — лаговая скорость, содержит инструментальные и методические погрешности и в общем случае не равна относительной скорости корабля V0. Расстояние, вычисленное по показаниям счетчика лага (рол), также содержит погрешность.
Понятие об определении поправок лага
Ежегодно на кораблях ВМФ проводится комплекс мероприятий, называемый определение маневренных элементов. Одной из его составляющих является определение относительной скорости Vo, соответствующей частоте работы движителей No и поправок относительного лага — ∆Л%.
Для определения скорости используются специально оборудованные полигоны, называемые мерными линиями, на которых некоторым образом создается эталонное расстояние Sэ, например, с помощью створных знаков, как показано на рисунке:
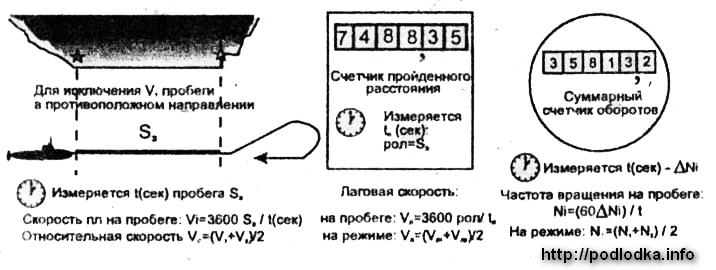
— относительная скорость корабля Vo на основных режимах движения (СПХ, ПХ, СХ, MX. СМХ);v — соответствующая ей частота вращения движителей по показаниям суммарных счетчиков оборотов — N0,
— лаговая скорость Vn по показаниям счетчика пройденного расстояния лага;
— коэффициент относительного лага: Кл = Vo / Vn;
Если Кл >1 (V0 >Vл) — лаг «отстает» — поправка лага ∆Л% — положительная; Если Кл <1 (V0
— оправка относительного лага АЛ% — относительная суммарная систематическая погрешность лага, взятая с обратным знаком: ∆Л%=[(Vo — Vn) / Vn] −100%; ∆Л% = 100 * (Kл — 1).
Полученные на мерной линии результаты заносятся в Справочные таблицы штурмана (СТШ) для расчета пройденного пл расстояния в процессе плавания и в техническую документацию лага.
Расчет пройденного кораблем расстояния
а) по показаниям счетчика лага:
— так как относительная скорость корабля V0=Vn * Kл, то для получения пройденного кораблем расстояния относительно поверхности воды по показаниям относительного лага S„ необходимо разность двух последовательных отсчетов лага ОЛ2- ОЛ1 = рол исправить коэффициентом лага; Sл = (0Л2- ОЛ1) * Кл = рол * Кл.
Например: в момент окончания поворота на заданный курс показания счетчика лага составили: ол1=17,4. В точке начала поворота на новый курс показания счетчика составили: олг=25,9. Коэффициент лага: Кл=1,05. Пройденное кораблем расстояние на заданном курсе составляет:
Sn= (ОЛ2- 0Л1) * Кл =(25,9 — 17,4) *1,05 = 8,93 мили
— для перехода от поправки лага к коэффициенту используется выражение: Кл = 1 + ∆Л% /100;
Напртшер: если поправка-лага Л%=+5%, то Кл = 1 + 5% /100 =1,05,
б) по относительной скорости и времени плавания:
— из справочных таблиц штурмана по заданной частоте вращения движителей N0 выбрать относительную скорость корабля Vоб;
— рассчитать пройденное расстояние Sоб =Vоб * t, где t — время плавания.
Например: пл следует заданным курсом, имея частоту вращения движителей No=100/100 об/мин. Время плавания заданным курсом t составило 1 час 24 минуты. Рассчитать пройденное пл расстояние.
1. Из СТШ выбрать Vоб = 9,0 узлов.
2. Время плавания: t =1час 24 мин перевести в часы: t = 1,4 часа.
3. Пройденное пл расстояние: So6 = Vo6 • t = 9,0×1,4 = 12;6 мили.
Способ расчета пройденного расстояния по скорости и времени плавания является резервным при выходе из строя относительного лага, а при работе лага используется для контроля работы счетчика пройденного расстояния: в процессе плавания пл сравнить: Sэ=Sоб.
При соблюдении равенства пройденного расстояния делается вывод:
— лаг работает исправно;
— нет промаха в расчете счислимого места корабля.