Как найти отрицание числа - AvtoShod.ru - решение различных проблем

Что такое отрицание в математике?

В математике отрицание утверждения противоположное данному математическому утверждению. Если «P» — утверждение, то отрицание утверждения P представлено ~P. … Таким образом, если данное утверждение истинно, то отрицание данного утверждения ложно.

Что такое пример отрицания?

Отрицание – это отказ или отрицание чего-либо. Если ваш друг считает, что вы должны ему пять долларов, а вы говорите, что не должны, ваше утверждение является отрицанием. … «Я не убивал дворецкого» может быть отрицанием, наряду с «Я не знаю, где сокровище». Акт произнесения одного из этих утверждений также является отрицанием.

Что такое отрицание в математической логике?

В логике отрицание, также называемое логическим дополнением, операция, переводящая предложение в другое предложение «не», написанное или . Интуитивно интерпретируется как истинное, когда ложное, и ложное, когда истинное.

Что такое правило отрицания?

Следующая тема, связанная с кольцом. Вычисляет вероятность наступления события при заданной вероятности его ненаступления (или наоборот). Р(А) = 1 – Р(неА) Например, вероятность получить хотя бы один туз за два розыгрыша из стандартной колоды — это отрицание того, что туза вообще не будет.

Что такое отрицание и как его показать?

Если вы хотите выразить противоположное значение определенного слова или предложения, вы можете сделать это, вставив отрицание. Отрицания такие слова, как нет, нет и никогда. Например, если вы хотите выразить противоположность слову «я здесь», вы можете сказать, что меня здесь нет.

Что такое отрицание P → Q?

Отрицание «P и Q» есть «не-P или не-Q». Отрицание «P или Q» есть «не-P и не-Q».

Как найти отрицание числа?

Отрицательная версия положительного числа называется его отрицанием. Например, −3 — это отрицание положительного числа 3. Сумма числа и его отрицания равна нулю: 3 + (−3) = 0.

Смотрите также, что произойдет, если все растения погибнут.

Что такое математические квантификаторы?

Квантификаторы — это выражения или фразы, указывающие на количество объектов, к которым относится утверждение. В математической логике есть два квантора: кванторы существования и всеобщности. … ‘Некоторые слова и фразы в утверждении, которые указывают на универсальный квантор, это ‘каждый’, ‘всегда’ или ‘для каждого’.

Является ли отрицание тем же, что и инверсия?

Чтобы образовать инверсию условного оператора, возьмите отрицание как гипотезы, так и вывода

. Обратное к фразе «Если идет дождь, то они отменяют школу» звучит так: «Если не идет дождь, то они не отменяют школу».

…

Обратное, обратное, контрапозитивное.

Заявление	Если р, то q.
Обратный	Если не p, то не q.
Противоположный	Если не q, то не p.

Что такое отрицание 2 является простым числом?

5 Какое утверждение является отрицанием «Два — простое число» и каково истинное значение этого отрицания? 6 Учитывая утверждение: Один — простое число. Что такое отрицание и истинность отрицания?

…

1)	Утверждение ложно, а его отрицание истинно.
4)	Утверждение истинно, а его отрицание ложно.

Как написать отрицание по математике?

В математике отрицание утверждения противоположное данному математическому утверждению. Если «P» — утверждение, то отрицание утверждения P представлено ~P. Для обозначения отрицания утверждения используются символы «~» или «¬». Например, данное предложение звучит так: «У собаки Арджуна черный хвост».

Как делать отрицание в математике?

Что такое отрицание или устранение?

Отрицание Устранение правило вывода что позволяет нам удалять двойные отрицания.

Что такое простое отрицание приведите 5 примеров?

Некоторые слова, такие как когда-либо, кто-нибудь, кто-нибудь, что-нибудь, где-нибудь, вместо никогда, никто, никто, ничего, нигде и т. д. представляют Отрицание. Примеры: Я не думаю, что он когда-либо сможет достичь в течение времени.

Что такое условность в математике?

Одним из наиболее часто используемых типов операторов в математике являются так называемые условные операторы. Для заданных операторов P и Q оператор вида «Если P, то Q» называется условным оператором. … Утверждение «Если P, то Q» означает что Q должно быть истинным всякий раз, когда истинно P.

Что значит привести пример?

1 : тот, который служит образцом для подражания или не для подражания пример. 2: наказание, наложенное на кого-то в качестве предупреждения и для других: так наказывается человек. 3: тот, который представляет всю группу или тип.

Что такое П К?

Предложение вида «если p, то q» или «p влечет q», представленное «p → q», называется условное предложение. … Предложение p называется гипотезой или антецедентом, а суждение q — заключением или следствием. Обратите внимание, что p → q всегда истинно, за исключением случаев, когда p истинно, а q ложно.

Является ли P → Q → [( P → Q → Q тавтологией Почему или почему нет?

(p → q) и (q ∨ ¬p) логически эквивалентны. Итак, (p → q) ↔ (q ∨ ¬p) является тавтологией. … У нас есть ряд правил логической эквивалентности.

Что такое противоположность P → Q?

Противоположный условному утверждению вида «Если р, то q» есть «Если ~q, то ~p”. Символически противоположным p q является ~ q ~ p.

Что такое обратное в математике?

Обратное утверждение образованы заменой гипотезы и заключения. Обратное утверждение «Если две прямые не пересекаются, то они параллельны» звучит так: «Если две прямые параллельны, то они не пересекаются». Обратное выражение «если p, то q» равносильно «если q, то p».

Что такое дополнение 2s?

Чтобы получить дополнение до 2 двоичного числа, Дополнение заданного числа до 1 плюс 1 до младшего значащего бита (LSB). Например, дополнение до 2 двоичного числа 10010 равно (01101) + 1 = 01110.

…

Дополнение до 2 двоичного числа.

Двоичный номер	1 дополнение	дополнение 2
101	010	011
110	001	010
111	000	001

Посмотрите также, какой тип реакции происходит, когда атомы или молекулы перестраиваются с образованием новых веществ?

В чем разница между минусом и минусом?

В качестве прилагательных разница между отрицательным и минусовым

в том, что отрицательный не является положительным или нейтральным в то время как минус (математика) отрицательный.

Что такое квантификаторы в C?

Квантификаторы используется в количественных выражениях, в которых свободные переменные связаны кванторами. Другими словами, переменные предикатов квантифицируются кванторами. В логике предикатов используются два хорошо известных квантора: квантор всеобщности и квантор существования.

Что такое квантифицированное выражение?

Количественное выражение определяет, удовлетворяют ли некоторые или все элементы последовательности определенному условию. Например, если вы хотите узнать, поступил ли какой-либо из товаров в заказе из отдела аксессуаров, вы можете использовать выражение, показанное в примере 6-8. Это выражение вернет true.

ЧТО ОЗНАЧАЕТ, ЧТО A подразумевает B?

«А подразумевает Б» означает, что B по крайней мере так же верно, как A, то есть истинностное значение B больше или равно истинностному значению A. Теперь истинностное значение истинного утверждения равно 1, а истинностное значение ложного утверждения равно 0; нет отрицательных значений истинности.

В чем разница между конверсией и отрицанием?

Обратное: «Если предмет имеет цвет, то он красный». Объекты могут иметь другие цвета, поэтому обратное утверждение неверно. Отрицание – это «Существует красный объект, который не имеет цвета». Это утверждение ложно, потому что исходное утверждение, которое оно отрицает, истинно.

Как противопоставить утверждение?

Противопоставление: выполнение преобразования предложения (т. е. замена подлежащего сказуемым). а затем замените как подлежащие, так и сказуемые термины их дополнениями. Пример: Давайте попробуем: «Все собаки — млекопитающие».

Что такое контрпример?

Математические слова: противопоставление. Переключение гипотезы и заключения условного утверждения и отрицание того и другого. Например, противопоставление «Если идет дождь, то трава мокрая». «Если трава не мокрая, значит, дождя нет».

Что такое пример обратного утверждения?

Обратное утверждение получается путем замены позиций «p» и «q» в заданном условии. Например, «Если Клифф хочет пить, она пьет воду” является условием. Обратное утверждение: «Если Клифф пьет воду, значит, она хочет пить».

Смотрите также, как размножаются пориферы.

Как вы делаете отрицание?

Следует иметь в виду, что если утверждение истинно, то его отрицание ложно (а если утверждение ложно, то его отрицание истинно).

…

Резюме.

Заявление	Отрицание
«А или Б»	«не А и не Б»
«А и Б»	«не А или не Б»
«если А, то Б»	«А, а не Б»
«Для всех х А(х)»	«Существуют такие х, что не А(х)».

Сколько делителей имеет число 420?

Есть 24 фактора всего 420. 1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 20, 21, 28, 30, 35, 42, 60, 70, 84, 105, 140, 210 и 420 — множители которые делят 420 поровну без остатка.

Какой символ отрицания утверждения Z?

∀x∈Z Поскольку данное утверждение ложно, его отрицание истинно.

…

Определение.

	Символическая форма	английская форма
Отрицание	(∀x∈Z)(∃y∈Z)(x+y≠0)	Существует целое число x такое, что для каждого целого числа y x+y≠0.

Читается как не п?

~ {Р} или {neg P} читается как «не P». Помните: оператор отрицания, обозначаемый символом ~ или neg, принимает истинностное значение исходного утверждения, а затем выводит прямо противоположное его истинностное значение. Другими словами, отрицание просто переворачивает истинностное значение данного утверждения.

Каковы 3 характеристики математического языка?

Это: • точный (способность делать очень тонкие различия); • лаконичен (умею говорить кратко); • мощный (способный относительно легко выражать сложные мысли).

Отрицание утверждения | Не запоминай

Логические операторы — отрицание, соединение и дизъюнкция

Отрицание универсальных и экзистенциальных кванторов

Отрицание условного оператора

Источник

Логическая операция инверсия — унарная операция над высказываниями, в результате выполнения которой высказывание становится противоположным исходному высказыванию.

Другие названия отрицания — отрицание или логическое НЕ.

Инверсия или отрицание изучается в информатике при рассмотрении раздела алгебра логики.

В естественных языках отрицанию соответствует частица ‘не‘ или слова ‘неверно, что‘. Например, если высказывание A = ‘Москва — столица России’, то его отрицание будет звучать как ‘Москва не столица России’.

В языках программирования для отрицания используют обозначение ‘not‘ или восклицательный знак ‘!‘ (например, not(x = 5) или !(x<3)).

Для обозначения отрицания используют символ ¬ или черту над высказыванием. Например, отрицание A можно обозначить либо ¬A, либо overline{A}.

Как набрать знак инверсии на клавиатуре

В Word чтобы набрать символ ¬ необходимо нажать левый Alt, и удерживая его на цифровой клавиатуре (которая справа клавиатуры) набрать цифры 0172. Т. е. символ ¬ — это Alt+0172. Режим Num Lock должен быть включен.

Чтобы сделать черту над буквой, необходимо зайти в пункт меню Вставка -> Формула (или Уравнение). После этого на панели инструментов найти диакритические знаки и среди них нужный нам знак с чертой над буквой.

Таблица истинности инверсия

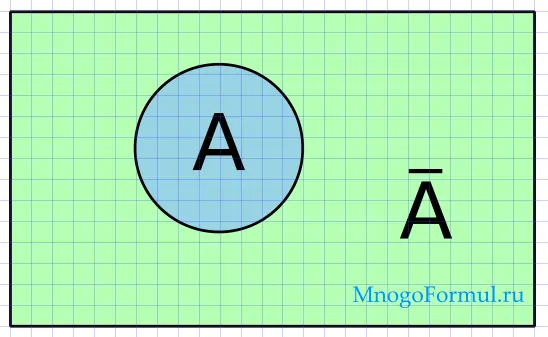
Отрицание и круги Эйлера

Обозначим высказывание A кругом, тогда отрицание A будет располагаться снаружи круга.

Источник

From Wikipedia, the free encyclopedia

Negation

NOT

Definition
Truth table
Logic gate
Normal forms
Disjunctive
Conjunctive
Zhegalkin polynomial
Post’s lattices
0-preserving	no
1-preserving	no
Monotone	no
Affine	yes
v t e

In logic, negation, also called the logical complement, is an operation that takes a proposition to another proposition «not «, standing for « is not true», written neg P , or . It is interpreted intuitively as being true when is false, and false when is true.^[1]^[2] Negation is thus a unary logical connective. It may be applied as an operation on notions, propositions, truth values, or semantic values more generally. In classical logic, negation is normally identified with the truth function that takes truth to falsity (and vice versa). In intuitionistic logic, according to the Brouwer–Heyting–Kolmogorov interpretation, the negation of a proposition is the proposition whose proofs are the refutations of .

Definition[edit]

Classical negation is an operation on one logical value, typically the value of a proposition, that produces a value of true when its operand is false, and a value of false when its operand is true. Thus if statement is true, then neg P (pronounced «not P») would then be false; and conversely, if neg P is true, then would be false.

The truth table of neg P is as follows:

Negation can be defined in terms of other logical operations. For example, neg P can be defined as (where is logical consequence and bot is absolute falsehood). Conversely, one can define bot as for any proposition Q (where land is logical conjunction). The idea here is that any contradiction is false, and while these ideas work in both classical and intuitionistic logic, they do not work in paraconsistent logic, where contradictions are not necessarily false. In classical logic, we also get a further identity, can be defined as , where lor is logical disjunction.

Algebraically, classical negation corresponds to complementation in a Boolean algebra, and intuitionistic negation to pseudocomplementation in a Heyting algebra. These algebras provide a semantics for classical and intuitionistic logic, respectively.

Notation[edit]

The negation of a proposition p is notated in different ways, in various contexts of discussion and fields of application. The following table documents some of these variants:

Notation	Plain Text	Vocalization
	¬p , 7p^[3]	Not p
	~p	Not p
	-p	Not p
Np		En p
	p’	p prime, p complement
	̅p	p bar, Bar p
	!p	Bang p Not p

The notation Np is Łukasiewicz notation.

In set theory, is also used to indicate ‘not in the set of’: is the set of all members of U that are not members of A.

Regardless how it is notated or symbolized, the negation neg P can be read as «it is not the case that P«, «not that P«, or usually more simply as «not P«.

Properties[edit]

Double negation[edit]

Within a system of classical logic, double negation, that is, the negation of the negation of a proposition , is logically equivalent to . Expressed in symbolic terms, . In intuitionistic logic, a proposition implies its double negation, but not conversely. This marks one important difference between classical and intuitionistic negation. Algebraically, classical negation is called an involution of period two.

However, in intuitionistic logic, the weaker equivalence does hold. This is because in intuitionistic logic, neg P is just a shorthand for , and we also have . Composing that last implication with triple negation implies that .

As a result, in the propositional case, a sentence is classically provable if its double negation is intuitionistically provable. This result is known as Glivenko’s theorem.

Distributivity[edit]

De Morgan’s laws provide a way of distributing negation over disjunction and conjunction:

{displaystyle neg (Plor Q)equiv (neg Pland neg Q)}

, and

{displaystyle neg (Pland Q)equiv (neg Plor neg Q)}

Linearity[edit]

Let oplus denote the logical xor operation. In Boolean algebra, a linear function is one such that:

If there exists ${displaystyle a_{0},a_{1},dots ,a_{n}in {0,1}}$ ,
${displaystyle f(b_{1},b_{2},dots ,b_{n})=a_{0}oplus (a_{1}land b_{1})oplus dots oplus (a_{n}land b_{n})}$ ,
for all ${displaystyle b_{1},b_{2},dots ,b_{n}in {0,1}}$ .

Another way to express this is that each variable always makes a difference in the truth-value of the operation, or it never makes a difference. Negation is a linear logical operator.

Self dual[edit]

In Boolean algebra, a self dual function is a function such that:

${displaystyle f(a_{1},dots ,a_{n})=neg f(neg a_{1},dots ,neg a_{n})}$ for all
${displaystyle a_{1},dots ,a_{n}in {0,1}}$ .
Negation is a self dual logical operator.

Negations of quantifiers[edit]

In first-order logic, there are two quantifiers, one is the universal quantifier forall (means «for all») and the other is the existential quantifier exists (means «there exists»). The negation of one quantifier is the other quantifier ( and ). For example, with the predicate P as «x is mortal» and the domain of x as the collection of all humans, means «a person x in all humans is mortal» or «all humans are mortal». The negation of it is , meaning «there exists a person x in all humans who is not mortal», or «there exists someone who lives forever».

Rules of inference[edit]

There are a number of equivalent ways to formulate rules for negation. One usual way to formulate classical negation in a natural deduction setting is to take as primitive rules of inference negation introduction (from a derivation of to both and neg Q , infer neg P ; this rule also being called reductio ad absurdum), negation elimination (from and neg P infer ; this rule also being called ex falso quodlibet), and double negation elimination (from infer ). One obtains the rules for intuitionistic negation the same way but by excluding double negation elimination.

Negation introduction states that if an absurdity can be drawn as conclusion from then must not be the case (i.e. is false (classically) or refutable (intuitionistically) or etc.). Negation elimination states that anything follows from an absurdity. Sometimes negation elimination is formulated using a primitive absurdity sign bot . In this case the rule says that from and neg P follows an absurdity. Together with double negation elimination one may infer our originally formulated rule, namely that anything follows from an absurdity.

Typically the intuitionistic negation neg P of is defined as . Then negation introduction and elimination are just special cases of implication introduction (conditional proof) and elimination (modus ponens). In this case one must also add as a primitive rule ex falso quodlibet.

Programming language and ordinary language[edit]

As in mathematics, negation is used in computer science to construct logical statements.

if (!(r == t))
{
    /*...statements executed when r does NOT equal t...*/
}

The exclamation mark «!» signifies logical NOT in B, C, and languages with a C-inspired syntax such as C++, Java, JavaScript, Perl, and PHP. «NOT» is the operator used in ALGOL 60, BASIC, and languages with an ALGOL- or BASIC-inspired syntax such as Pascal, Ada, Eiffel and Seed7. Some languages (C++, Perl, etc.) provide more than one operator for negation. A few languages like PL/I and Ratfor use ¬ for negation. Most modern languages allow the above statement to be shortened from if (!(r == t)) to if (r != t), which allows sometimes, when the compiler/interpreter is not able to optimize it, faster programs.

In computer science there is also bitwise negation. This takes the value given and switches all the binary 1s to 0s and 0s to 1s. See bitwise operation. This is often used to create ones’ complement or «~» in C or C++ and two’s complement (just simplified to «-» or the negative sign since this is equivalent to taking the arithmetic negative value of the number) as it basically creates the opposite (negative value equivalent) or mathematical complement of the value (where both values are added together they create a whole).

To get the absolute (positive equivalent) value of a given integer the following would work as the «-» changes it from negative to positive (it is negative because «x < 0» yields true)

unsigned int abs(int x)
{
    if (x < 0)
        return -x;
    else
        return x;
}

To demonstrate logical negation:

unsigned int abs(int x)
{
    if (!(x < 0))
        return x;
    else
        return -x;
}

Inverting the condition and reversing the outcomes produces code that is logically equivalent to the original code, i.e. will have identical results for any input (note that depending on the compiler used, the actual instructions performed by the computer may differ).

This convention occasionally surfaces in ordinary written speech, as computer-related slang for not. For example, the phrase !voting means «not voting». Another example is the phrase !clue which is used as a synonym for «no-clue» or «clueless».^[4]^[5]

Kripke semantics[edit]

In Kripke semantics where the semantic values of formulae are sets of possible worlds, negation can be taken to mean set-theoretic complementation^{[citation needed]} (see also possible world semantics for more).

References[edit]

^ Weisstein, Eric W. «Negation». mathworld.wolfram.com. Retrieved 2 September 2020.
^ «Logic and Mathematical Statements — Worked Examples». www.math.toronto.edu. Retrieved 2 September 2020.
^ Used as makeshift in early typewriter publications, e.g. Richard E. Ladner (January 1975). «The circuit value problem is log space complete for P». ACM SIGACT News. 7 (101): 18–20. doi:10.1145/990518.990519.
^ Raymond, Eric and Steele, Guy. The New Hacker’s Dictionary, p. 18 (MIT Press 1996).
^ Munat, Judith. Lexical Creativity, Texts and Context, p. 148 (John Benjamins Publishing, 2007).

External links[edit]

Horn, Laurence R.; Wansing, Heinrich. «Negation». In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
«Negation», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
NOT, on MathWorld

Tables of Truth of composite clauses

«Table of truth for a NOT clause applied to an END sentence». Archived from the original on 1 March 2000.
«NOT clause of an END sentence». Archived from the original on 1 March 2000.
«NOT clause of an OR sentence». Archived from the original on 17 January 2000.
«NOT clause of an IF…THEN period». Archived from the original on 1 March 2000.

Источник

ческого сложения, аргументами которой являются логические переменные А и В. Значение логической функции можно определить с помощью таблицы истинности данной функции, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов (таблица 2).

Таблица 2 – Таблица истинности функции логического сложения (дизъюнкция)

А	В	F = A v B (A + B)
0	0	0

0	1	1

1	0	1

1	1	1

По таблице истинности легко определить истинность составного высказывания, образованного с помощью операции логического сложения. Рассмотрим, например, составное высказывание «2 • 2 = 4 или 3 • 3 = 10».

Первое простое высказывание истинно (А = 1), а второе высказывание ложно (В = 0); по таблице определяем, что логическая функция принимает значение истина (F = 1), то есть данное составное высказывание истинно.

Присоединение частицы «не» к высказыванию называется операцией логиче-

ского отрицания.

Операция логического отрицания является унарной, так как имеет один аргу-

мент. Иначе её называют инверсией, дополнением, НЕ и обозначают Ā или ¬А,

NOT A.

Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное — истинным.

Пусть А = «Два умножить на два равно четырём» — истинное высказывание, тогда высказывание F = «Два умножить на два не равно четырём», образованное с помощью операции логического отрицания, — ложно.

Образуем высказывание F, являющееся логическим отрицанием А:

F = Ā

Истинность такого высказывания задаётся таблицей истинности функции логического отрицания (таблица 3).

Таблица 3 – Таблица истинности функции логического отрицания (инверсия)

А	F=Ā

0	1

1	0

Истинность высказывания, образованного с помощью операции логического отрицания, можно легко определить с помощью таблицы истинности.

Например, высказывание:

«Два умножить на два не равно четырём» ложно (А = 0), а полученное из него в результате логического отрицания высказывание

«Два умножить на два равно четырём» истинно (F = 1).

2.4.Логическое следование (импликация)

Операцию логического следования иначе называют импликацией и для обозначения используют символ → «следовательно» и выражается словами ЕСЛИ … , ТО ….

Логическое следование: ИМПЛИКАЦИЯ – связывает два простых логических выражения, из которых первое является условием (А), а второе (В) – следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно (таблица 4).

Импликацией А→В называется высказывание, которое ложно тогда и только тогда, когда А истинно и В ложно.

Таблица 4 – Таблица истинности функции логического следования (импликация)

А	В	А→В

1	1	1

1	0	0

0	1	1

0	0	1

2.5.Логическое тождество (эквиваленция)

Операцию логического тождества обозначают символами =, ↔, ~. Интуитивно можно догадаться, что высказывания эквивалентны (равносиль-

ны), когда их значения истинности одинаковы.

Например, эквивалентны высказывания: «железо тяжёлое» и «пух лёгкий», так же как и высказывания: «железо лёгкое» и «пух тяжёлый». Обозначим эквиваленцию символом ↔ и запись «А ↔ В» будем читать «А эквивалентно В», или «А равносильно В», или «А, если и только если В».

Таким образом, эквиваленцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда оба эти высказывания А и В истинны или оба ложны.

Высказывание типа «А, если и только если В» можно заменить высказыванием «Если А, то В и, если В, то А».

Следовательно, функцию эквиваленции можно заменить комбинацией функций импликации и конъюнкции.

Запишем таблицу истинности для эквиваленции (таблица 5):

Таблица 5 – Таблица истинности функции логического тождества (эквиваленция)

А	В	А ↔ В
1	1	1
1	0	0
0	1	0
0	0	1

Приведём примеры записи сложных высказываний с помощью обозначения логических связок:

«Быть иль не быть – вот в чём вопрос» (В. Шекспир) А V ¬ A ↔ В. «Если хочешь быть красивым, поступи в гусары» (К. Прутков) А ↔ В.

2.6.Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Операция исключающее ИЛИ (неравнозначность, сложение по модулю два) обозначается символом и отличается от логического ИЛИ только при A=1 и B=1.

Таким образом, неравнозначность двух высказываний Х1 и Х2 называют такое высказывание Y, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.

Определение данной операции может быть записано в виде таблицы истинности (таблица 6):

Таблица 6 – Таблица истинности операции «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Х1	Х2	Y

1	1	0

1	0	1

0	1	1

0	0	0

Как видно из таблицы 6, логика работы элемента соответствует его названию. Это тот же элемент «ИЛИ» с одним небольшим отличием. Если значение на обоих входах равно логической единице, то на выходе элемента «ИСКЛЮЧА-

ЮЩЕЕ ИЛИ», в отличие от элемента «ИЛИ», не единица, а ноль.

Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» фактически сравнивает на совпадение два двоичных разряда.

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет своё название и обозначение (таблица 7).

Таблица 7 – Основные логические операции

Обозначение	Читается	Название операции	Альтернатив-
операции			ные обозначе-
			ния
¬	НЕ	Отрицание (инверсия)	Черта сверху
^	И	Конъюнкция (логическое	&
	умножение)

v	ИЛИ	Дизъюнкция (логическое	+
	сложение)

→	Если … то	Импликация
↔	Тогда и толь-	Эквиваленция	~
ко тогда

XOR	Либо … либо	ИСКЛЮЧАЮЩЕЕ ИЛИ
		(сложение по модулю 2)

3.Порядок выполнения логических операций

всложном логическом выражении

Система логических операций инверсии, конъюнкции, дизъюнкции позволяет построить сколь угодно сложное логическое выражение.

При вычислении значения логического выражения принят определённый порядок выполнения логических операций.

1.Инверсия.

2.Конъюнкция.

3.Дизъюнкция.

4.Импликация.

5.Эквивалентность.

Для изменения указанного порядка выполнения операций используются скобки.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Мы знаем, что если сложить два или несколько натуральных чисел, то в результате получим натуральное число. Если перемножать натуральные числа между собой, то в результате всегда получаются натуральные числа. А какие числа будут в результате, если из одного натурального числа вычесть другое натуральное число? Если из большего натурального числа вычесть меньшее, то результат тоже будет натуральным числом. А какое число будет , если из меньшего числа вычесть большее? Например, если из 5 вычесть 7. Результат такого действия уже не будет натуральным числом, а будет числом меньше нуля, которое мы напишем как натуральное, но со знаком «минус», так называемым, отрицательным натуральным числом. На этом уроке мы познакомимся с отрицательными числами. Поэтому мы расширяем множество натуральных чисел, добавляя к нему «0» и целые отрицательные числа. Новое расширенное множество будет состоять из чисел:

…-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6…

Эти числа называются целыми. Следовательно, результат нашего примера 5 -7 = -2 будет целым числом.

Определение. Целые числа – это натуральные, отрицательные натуральные и число «0».

Изображение этого множества мы видим на градуснике для измерения температуры на улице.

Температура может быть с «минусом», т.е. отрицательной, может быть с «плюсом» т.е. положительной. Температура 0 градусов не положительная не отрицательная, число 0 – граница, которая отделяет положительные числа от отрицательных.

Изобразим целые числа на числовой оси.

Рисунок оси

Мы видим, что на числовой оси существует бесконечное множество чисел . Положительные и отрицательные числа разделены между собой нулем. Отрицательные целые числа, например -1, читаются как «минус единица» или «отрицательная единица».

Положительные целые числа, например «+3» читается как положительная 3 или просто «три», то есть у положительных (натуральных) чисел знак «+» не пишется и слово «положительное» не произносится.

Примеры: отметь на числовой оси +5, +6, -7, -3, -1, 0 и т.д.

При движении вправо по числовой оси числа увеличиваются, а при движении влево — уменьшаются. Если мы хотим увеличить число на 2, мы движемся вправо по координатной оси на 2 единицы. Пример: 0+2=2; 2+2=4; 4+2=6 и т. д. И наоборот, если мы хотим уменьшить число на 3 мы будем двигаться влево на 3 единицы. Например: 6-3=3; 3-3=0; 0-3=-3; и т.д.

1. Попробуй увеличить число (-4) за 3 шага, увеличивая каждый раз на 2 единицы.

Двигаясь по числовой оси, как показано на рисунке, мы получим в результате 2.

2. Уменьши число 6 за шесть шагов, уменьшая его за каждый шаг на 2 единицы.

3. Увеличь число (-1) за три шага, увеличивая его на 4 единицы на каждом шаге.

С помощью координатной прямой легко сравнивать целые числа: из двух чисел больше то, которое на координатной прямой расположено правее, а меньше то, что стоит левее.

4. Сравни числа, поставив знак > или < , для удобства сравнения изобрази их на координатной прямой:

-3 и 2; 0 и -5; -34 и -67; -72 и 0 и т.д.

5. Вспомни, как мы отмечали на координатном луче точки с натуральными координатами. Точки принято называть заглавными латинскими буквами. Нарисуй координатную прямую, и взяв удобный единичный отрезок, изобрази точки с координатами:

А) А(10),В(20),С(30),М(-10),N(-20)
Б) С(100),В(200),К(300),F(-100)
В) U(1000),Е(2000),R(-3000)

6. Запиши все целые числа, расположенные между -8 и 5, между -15 и -7, между -1 и 1.

Сравнивая числа, мы должны уметь ответить на сколько единиц одно число больше или меньше другого.

Нарисуем координатную прямую. Изобразим на ней точки с координатами от -5 до 5. Число 3 на две единицы меньше 5, на единицу меньше 4, на 3 единица больше нуля. Число -1 на единицу меньше нуля, на 2 единицы больше -3.

7. Ответь, на сколько единиц:

-3 меньше 4; -2 меньше 3; -5 меньше -4; 2 больше -1; 0 больше -5; 4 больше -1

8. Нарисуй координатную прямую. Выпиши 7 чисел, каждое из которых на 2 единицы меньше предыдущего, начиная с 6. Какое у этого ряда последнее число ? Сколько может быть всего таких чисел, если количество выписываемых чисел не ограничивать?

9. Выпиши 10 чисел, каждое из которых на 3 единицы больше предыдущего начиная с (-6). Сколько таких чисел может существовать, если ряд не ограничивать десятью?

Противоположные числа.

На числовой оси для каждого положительного числа (или натурального) существует отрицательное число, расположенное слева от нуля на таком же расстоянии. Например: 3 и -3; 7 и -7; 11 и -11.

Говорят, что число -3 является противоположным числу 3, и наоборот, -3 противоположно 3.

Определение: Два числа, которые отличаются друг от друга только знаком называются противоположными.

Мы знаем, что если умножить число на +1, то число не изменится. А если число умножить на (-1), что будет? У такого числа поменяется знак. Например, если 7 умножить на (-1) или отрицательную единицу, то результат будет (-7), число становится отрицательным. Если (-10) умножить на (-1), то получим (+10), т. е. получаем уже положительное число. Таким образом, мы видим, что противоположные числа получаются простым умножением исходного числа на (-1). Мы видим на числовой оси, что у каждого числа существует только одно противоположное число. Например, у (4) противоположное будет (-4), у числа (-10) – противоположное будет (+10). Попробуем найти противоположное число у нуля. Его нет. Т.е. 0 – противоположен самому себе.

А теперь посмотрим на числовой оси, что получится, если сложить 2 противоположных числа. Мы получаем, что сумма противоположных чисел равна 0.

1. Игра: пусть игровое поле разделено пополам на два поля: левое и правое. Между ними проходит разделительная черта. На поле находятся числа. Переход через черту означает умножение на (-1), иначе при переходе через разделительную черту число становится противоположным.

Пусть в левом поле находится число (5). В какое число превратится (5), если пятерка перейдет разделительную полосу 1 раз? 2 раза? 3 раза?

2. Заполни следующую таблицу:

Исходные числа	Противоположные числа
6
-8
-9
13
23
-12
-4
-1

3. Из множества пар выбери пары противоположных. Сколько таких пар ты получил?

9 ; -100; 1009; -63; -7; -9; 3; -33; 25; -1009; -2; 1; 0; 100; 27; 345; -56; -345; 33; 7.

Сложение и вычитание целых чисел.

Сначала попробуем складывать или вычитать числа на числовой оси.

Сложение (или знак «+») означает движение вправо на числовой оси.

1+3 = 4

-1 + 4 = 3
-3 + 2 = -1

Вычитание( или знак»-«) означает движение влево на числовой оси

3 – 2 = 1
2 – 4 = -2
3 – 6 = -3
-3 + 5 = 2
-2 – 5 = -7
-1 + 6 = 5
1 – 4 = -3

Реши следующие примеры с помощью числовой оси:

-3+1=
2)-4-1=
4+1=
3+2=
3-5=
-5-1=
-2-7=
-1+3=
-1-4=
-6+7=

В Древнем Китае при составлении уравнений коэффициенты уменьшаемых и вычитаемых записывались цифрами разного цвета. Прибыль –обозначали красной краской, а убытки – синей. Пример, продали 3 быка и купили 2 лошади. Рассмотрим другой пример: хозяйка принесла на рынок картошку и продала ее за 300 рублей, эти деньги мы прибавим к имуществу хозяйки и напишем их как +300(красное), а затем она потратила 100 рублей (эти деньги мы запишем как(-100)(синие). Таким образом, получилось, что хозяйка вернулась с рынка с прибылью в 200рублей(или +200). Иначе, числа, записанные красной краской всегда складывали, а записанные синей краской вычитали. По аналогии, будем синей краской обозначать отрицательные числа.

Таким образом, мы можем все положительные числа считать выигрышем, а отрицательные проигрышем или долгом или потерей.

Пример: -4 + 9 = +5 результат (+5) можно рассматривать как выигрыш в какой-либо игре; после того, как сначала было проиграно 4 очка, а затем выиграно 9 очков, то в результате останется выигрыш в 5 очков. Реши следующие задачи:

11. В игре в лото Петя сначала выиграл 6 очков, затем проиграл 3 очка, затем опять выиграл 2 очка, затем проиграл 5 очков. Каков результат игры у Пети?

12 (*). Мама пожила конфеты в вазочку. Маша съела 4 конфеты, Миша съел 5 конфет, Оля съела 3 конфеты. Мама положила еще в вазочку 10 конфет , и в вазочке стало 12конфет. Сколько конфет было сначала в вазочке?

13. В доме одна лестница ведет из подвала на второй этаж. Лестница состоит из двух пролетов по 15 ступенек каждый (один из подвала на первый этаж, а второй с первого этажа на второй). Петя был на первом этаже. Сначала он поднялся по лестнице на 7ступенек вверх, а затем спустился на 13 ступенек вниз. Где оказался Петя?

14. Кузнечик прыгает вдоль числовой оси. Один прыжок кузнечика составляет 3 деления на оси. Кузнечик сначала делает 3 прыжка вправо, а затем 5 прыжков влево. Где окажется кузнечик после этих прыжков, если первоначально он находился в 1)«+1»;2) «-6»;3) «0»;4) «+5»;5) «-2»;6) «+3»;7) «-1».

До сих пор мы привыкли к тому, что рассматриваемые числа отвечали на вопрос «сколько». Но отрицательные числа не могут быть ответом на вопрос «сколько». В житейском смысле отрицательные числа связаны с долгом, проигрышем, с такими действиями, как недолил, недопрыгнул, недовесил и т.д. Во всех этих случаях мы просто вычитаем долг, проигрыш, недовес. Например,

На вопрос « Сколько будет «тысяча без 100»?», мы из 1000 должны вычесть 100 и получим 900.
Выражение «3 часа без четверти» – означает , что мы должны вычесть 15 мин из 3 часов. Получим, таким образом, 2часа 45 мин.

А теперь реши следующие задачи:

15. Саша покупал 200гр. масла, но недобросовестный продавец недовесил 5 гр. Какую массу масла купил Саша?

16.На беговой дистанции в 5 км. Володя сошел с дистанции, не добежав до финиша 200м. Какое расстояние Володя пробежал?

17. Заполняя трехлитровую банку соком мама не долила 100мл сока. Сколько сока получилось в банке?

18. Кино должно начаться без двадцати минут восемь. сколько минут Во сколько часов и во сколько минут должно начаться кино?

19.У Тани было 200руб. и она должна Пете 50 руб. После того, как она отдала долг, сколько денег осталось у Тани?

20. Петя с Ваней пошли в магазин. Петя захотел купить книгу за 5 рублей. Но у него оказалось только 3 рубля, и он занял у Вани 2 рубля и купил книгу. Сколько денег оказалось после покупки у Пети?

Решение:

3 — 5= -2 (из того, что у него было до покупки вычтем стоимость покупки, получим -2 рубля , то есть два рубля долга).

21. Днем температура воздуха была 3°тепла или +3°, а ночью 4° мороза или -4°. На сколько градусов понизилась температура? И на сколько градусов ночная температура меньше, чем дневная?

22. Таня договорилась встретиться с Володей без четверти семь. Во сколько часов и во сколько минут они договорились встретиться?

23. Тима с приятелем пошел в магазин покупать книгу, которая стоила 97 рублей. Но когда они пришли в магазин, то выяснилось, что книга подорожала, и стала стоить 105 рублей. Тима занял приятеля недостающую сумму, и все-таки купил книгу. Сколько денег Тима стал должен приятелю?

Источник

Что такое отрицание в математике?

Что такое пример отрицания?

Что такое отрицание в математической логике?

Что такое правило отрицания?

Что такое отрицание и как его показать?

Что такое отрицание P → Q?

Как найти отрицание числа?

Что такое математические квантификаторы?

Является ли отрицание тем же, что и инверсия?

Что такое отрицание 2 является простым числом?

Как написать отрицание по математике?

Как делать отрицание в математике?

Что такое отрицание или устранение?

Что такое простое отрицание приведите 5 примеров?

Что такое условность в математике?

Что значит привести пример?

Что такое П К?

Является ли P → Q → [( P → Q → Q тавтологией Почему или почему нет?

Что такое противоположность P → Q?

Что такое обратное в математике?

Что такое дополнение 2s?

В чем разница между минусом и минусом?

Что такое квантификаторы в C?

Что такое квантифицированное выражение?

ЧТО ОЗНАЧАЕТ, ЧТО A подразумевает B?

В чем разница между конверсией и отрицанием?

Как противопоставить утверждение?

Что такое контрпример?

Что такое пример обратного утверждения?

Как вы делаете отрицание?

Сколько делителей имеет число 420?

Какой символ отрицания утверждения Z?

Читается как не п?

Каковы 3 характеристики математического языка?

Отрицание утверждения | Не запоминай

Логические операторы — отрицание, соединение и дизъюнкция

Отрицание универсальных и экзистенциальных кванторов

Отрицание условного оператора

Как набрать знак инверсии на клавиатуре

Таблица истинности инверсия

Отрицание и круги Эйлера

Definition[edit]

Notation[edit]

Properties[edit]

Double negation[edit]

Distributivity[edit]

Linearity[edit]

Self dual[edit]

Negations of quantifiers[edit]

Rules of inference[edit]

Programming language and ordinary language[edit]

Kripke semantics[edit]

See also[edit]

References[edit]

Further reading[edit]

External links[edit]

2.4.Логическое следование (импликация)

2.5.Логическое тождество (эквиваленция)

2.6.Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Не пропустите также: