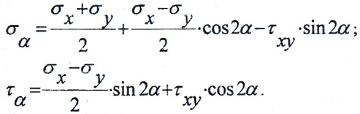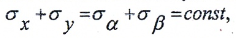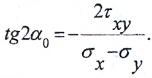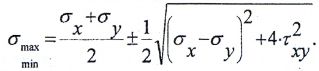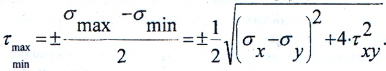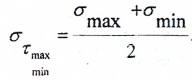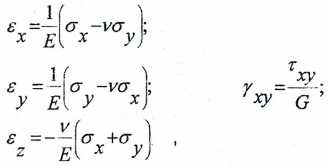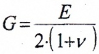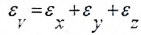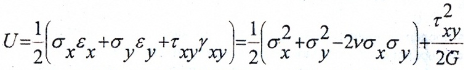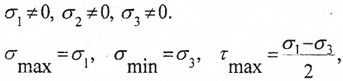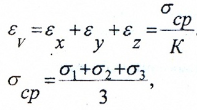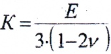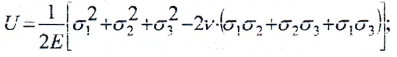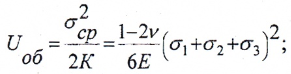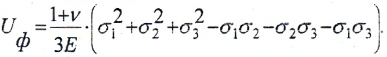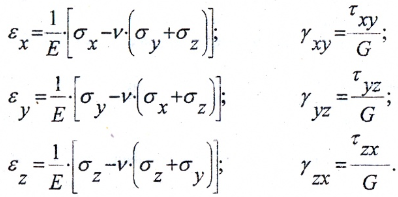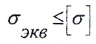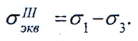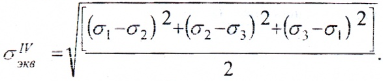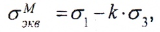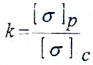Как найти относительное изменение объема - AvtoShod.ru

Относительное изменение объема.

Как
известно, при деформации происходит
изменение формы и объема тела. Рассмотрим
относительное изменение объема тела
при деформировании. Объем элементарного
прямоугольного параллелепипеда до
деформации

.

При
деформировании длина каждого ребра
может измениться на некоторую величину
D
и объем того же параллелепипеда после
деформирования будет

.

Тогда
относительное изменение объема может
быть вычислено следующим образом:

Раскрывая
скобки и пренебрегая слагаемыми более
высокого порядка малости по сравнению
с e
(e·e
≈ 0,
e·e·e
≈ 0),
получим

.

Подставляя
e
из
обобщенного закона Гука, получим

Учитывая,
что

,
запишем выражение для q
в виде

Из
формулы видно, что при положительных
направлениях главных напряжений
относительное изменение объема может
быть положительной величиной, если
только коэффициент Пуассона будет μ
<
0,5. Таким образом, получается, что для
всех существующих в природе материалов
коэффициент Пуассона изменяется в
пределах

и для большинства конструкционных
материалов он равен
0,2…0,3.

Также
можно отметить, что если коэффициент
Пуассона равен 0,5, то относительное
изменение объема равно нулю. Резина
имеет n
≈
0,5 , следовательно, при приложении
нагрузки её объём практически не
меняется, она ведет себя как несжимаемая
жидкость. Это свойство резины часто
используется в экспериментальной
практике.

Определим
также относительное изменение объема
при чистом сдвиге.

Так
как при чистом сдвиге

,
то

.

Таким
образом, относительное изменение объема
при чистом сдвиге равно нулю.

4.9. Допущения, применяемые в сопротивлении материалов

При
построении теории сопротивления
материалов принимают некоторые допущения
относительно структуры и свойств
материалов, а также о характере деформаций.

Основные
допущения:

1.
Материал конструкции однороден
(его свойства не зависят от величины
выделенного объема) и
изотропен
(свойства не зависят от направления
рассмотрения).

2.
В пределах малых величин деформации
материала подчиняются закону Гука. При
расчетах применим принцип
независимости действия сил.

3.
При решении большинства задач в
сопротивлении материалов принимается,
что материал конструкций обладает
абсолютной
упругостью,
т.е. геометрические размеры тела полностью
восстанавливаются после снятия нагрузки.

4.
Перемещения, возникающие под действием
внешних сил в упругом теле, малы по
сравнению с его размерами. Это допущение
называется
принципом
начальных размеров.
Допущение позволяет при составлении
уравнений равновесия пренебречь
изменениями формы и размеров конструкции.

5.
Предполагается, что в сечениях, достаточно
удаленных от мест приложения нагрузки,
характер распределения напряжений не
зависит от конкретного способа нагрузки.

6.
Плоские поперечные сечения стержня до
деформации остаются плоскими и после
деформации
(гипотеза
плоских сечений Бернулли).

7.
Ненагруженное тело свободно от внутренних
сил любой природы.

4.10. Общие принципы расчета конструкции. Теории прочности

Под
предельным опасным напряженным состоянием
понимается такое, при котором происходит
качественное изменение свойств материала
— переход от одного механического
состояния к другому. Для пластичных
материалов предельным обычно считается
напряженное состояние, соответствующее
возникновению заметных остаточных
деформаций, а для хрупкого — такое, при
котором начинается разрушение материала.
Предельное состояние материала допустить
нельзя, поэтому при расчете на прочность
ориентируются на так называемое
допускаемое состояние, которое
соответствует нагрузке, полученной
путем деления нагрузки, вызывающей
предельное состояние, на некоторый
коэффициент запаса. Если в двух напряженных
состояниях коэффициенты запаса равны,
то они называются равноопасными. Для
сравнения различных напряженных
состояний за эталон (эквивалент) принято
простое растяжение (сжатие) с главным
напряжением

.

Эквивалентное
напряжение

— это такое напряжение, которое следует
создать в растянутом образце, чтобы его
напряженное состояние было равноопасно
заданному напряженному состоянию.
Условие прочности записывается в виде

.

Теории
прочности представляют собой гипотезы
о критериях, определяющих условия
перехода материала в предельное
состояние.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

3.10. ИЗМЕНЕНИЕ ОБЪЕМА ТЕЛА Объем параллелепипеда до деформации Объем в деформированном состоянии Изменение объема тела Пренебрегая величинами второго и третьего порядка малости (произведения εi), получим = ε1 + ε2 + ε3. Относительное изменение объема равно сумме трех главных деформаций. Подставив εi из обобщенного закона Гука, получим θ=Δ=−μσ+σ112 2 + 3σ Для произвольно ориентированных площадок Анализ формул приводит к выводам: для материалов (каучук, парафин) с большим значением μ = 0,47 деформация будет происходить без изменения объема при любом из способов нагружения; для любого материала деформация происходит без изменения объема, если σ1+σ2+σ3 = 0. Например, при кручении σ2 = 0, σ3 = -σ1. Изменяется лишь форма (углы между гранями); изменение объема происходит без изменения формы, если σ1 = σ2 = σ3 = σ0 (гидростатическое сжатие); коэффициент Пуассона не может превышать значения 0,5, поскольку при μ > 0,5 материал уменьшается в объеме при растяжении. Примечание: формулы действительны при напряжениях, не превышающих предела пропорциональности

Источник

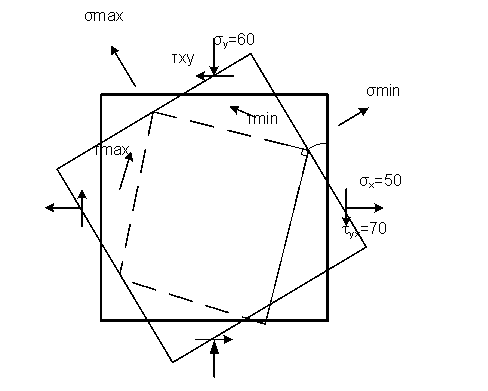
Пример решения задачи на теорию напряженного состояния.

Дано : σx=50 МПа; σy=60 МПа; τxy=70 МПа; E=1.3*105 МПа; μ=0.22

Требуется:

1. Определить величину главных напряжений и положение главных площадок;

2. Найти максимальные касательные напряжения τmax;

3. Определить относительные деформации и относительное изменение объёма;

4. Установить удельную потенциальную энергию деформации.

Решение.

1. Определим величину главных напряжений и положение главных площадок

В соответствии с правилом знаков, устанавливаем : σx=50 МПа ; σy=60 МПа ; τyx=-τxy

По формуле

σmax/min= определим величину главных напряжений.

σmax==125,2 МПа

σmin== — 15,2 МПа

Для определения положения главных площадок используем формулу:

tg2α0=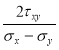== 14 = tg86°

откуда 2α0=86° и α0=43°

Для определения площадки, по которой действуют напряжения σmax , поворачиваем горизонтальную площадку (так как по ней действуют нормальные напряжения, больше, чем по вертикальной площадке) на угол α0=43° против часовой стрелки, т.е. в том направлении, в котором вектор касательного напряжения (на поворачиваемой площадке) стремиться вращать элементарный параллелепипед относительно его центра. Найденная площадка показана на рисунке.

2. Найдём максимальные касательные напряжения τmax

Максимальные касательные напряжения находим по формуле :

τmax/min===±140,4 МПа

Положения площадок сдвига (по которым касательные напряжения имеют максимальные значения) определяем по положениям главных площадок, к которым они наклонены под углами 45°. Экстремальные касательные напряжения действуют в направлениях от σmin к σmax.

3. Определим относительные деформации и относительное изменение объёма

Относительные деформации находим по формулам:

εx=(1/E)[σx—μσy]=1/(1.3*1011)[50-0.22*60]*106=2,83*10-4

εy=(1/E)[σy—μσx]=1/(1.3*1011)[60-0.22*50]*106=3,77*10-4

Относительное изменение объёма по формуле Ж

θ=εx+εy=(2,83+3,77)*10-4=6,6*10-4

4. Установим удельную потенциальную энергию деформации.

Удельную потенциальную энергию деформации находим по формуле:

u== ==57956,7 Дж/м3

Ответ : σmax=125,2 МПа; σmin= -15,2 МПа; τmax/min=±140,4 МПа; εx=2,83*10-4 ; εy=3,77*10-4 ; θ=6,6*10-4 ; u=57956,7 Дж/м3.

Источник

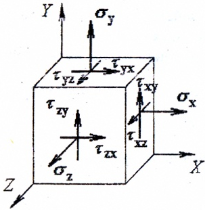
Теория напряженного состояния в окрестности точки деформируемого тела рассматривает совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку.

На площадках общего положения действуют нормальные и касательные напряжения (рис. 1).

Правило знаков для этих напряжений в сопротивлении материалов принимается следующим: положительные нормальные напряжения направлены от сечения, а положительные касательные напряжения стремятся повернуть элемент по направлению хода часовой стрелки.

Площадки, на которых отсутствуют касательные напряжения, называются главными площадками, а нормальные напряжения, действующие по этим площадкам, — главными напряжениями.

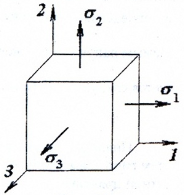
В любой точке деформируемого тела можно выделить три взаимно перпендикулярные главные площадки, по которым действуют главные напряжения σ₁, σ₂ и σ₃, причем σ₁ ≥ σ₂ ≥ σ₃.

Рис. 1

Если два главных напряжения из трех равны нулю, то такое напряженное состояние называется линейным или одноосным. Оно соответствует центральному (осевому) растяжению или сжатию и рассмотрено в предыдущем разделе.
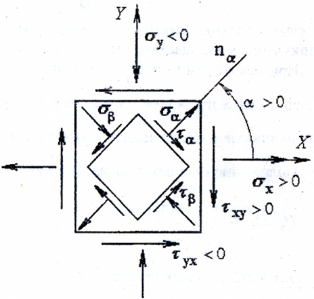
Если одно из трех главных напряжений равно нулю, то такое напряженное состояние называется плоским или двуосным. Пример плоского напряженного состояния показан на рис. 2.

Рис. 2

Одноименные напряжения на параллельных гранях бесконечно малого элемента численно равны друг другу. При плоском напряженном состоянии две противоположные грани всегда свободны от напряжений (на рис. 2 это фасадная и тыльная грани).

По закону парности касательных напряжений касательные напряжения на взаимно перпендикулярных площадках равны по величине и противоположны по знаку, т.е.
τ_xy=-τ_yx.

При повороте прямоугольного элемента на угол α напряжения на его гранях изменяются и вычисляются по формулам:

По закону парности касательных напряжений τ_α= -τ_β.

Величины σ связаны законом суммы нормальных напряжений

т.е. сумма величин нормальных напряжений, действующих по взаимно перпендикулярным площадкам, есть величина постоянная.

При некотором угле α₀ касательные напряжения равны нулю, нормальные напряжения по данной площадке в данной точке максимальны (σ_max), а на перпендикулярной площадке – минимальны (σ_min).

Положение главных площадок определяется по формуле

Значения главных напряжений вычисляются по выражению

Наибольшие касательные напряжения действуют на площадках, наклонных к главным под углом 45⁰ и рассчитываются по формулам:

Нормальные напряжения на этих площадках можно найти по формуле

Относительные линейные и угловые деформации ребер элемента можно вычислить на основании обобщенного закона Гука. Для плоского напряженного состояния

где

— модуль сдвига материала. Для стали G=80ГПа.

Относительное изменение объема материала в окрестностях исследуемой точки определяется по формуле

Удельная потенциальная энергия для плоского напряженного состояния

Напряженное состояние называется объемным или трехосным (рис. 3), если

Рис. 3

Относительное изменение объема

где K – модуль объемной деформации

Удельная потенциальная энергия упругой деформации:
— полная

— изменения объема

— изменения формы

Относительные деформации и напряжения связаны обобщенным законом Гука:

Теории прочности

Для проверки прочности материала при плоском и объемном напряженном состояниях используются гипотезы (теории) прочности.

Каждая гипотеза прочности высказывает свое предположение о том, какой фактор вызывает появление опасного (предельного) состояния.

В зависимости от принятой гипотезы определяют эквивалентное напряжение σ_экв и сравнивают его с допустимым напряжением на растяжение [σ], то есть условие прочности записывается следующим образом:

Приведем зависимости для вычисления эквивалентных напряжений по трем гипотезам прочности, наиболее широко применяемым в современной расчетной практике.

Гипотеза наибольших касательных напряжений (III теория прочности)

Четвертая (энергетическая) гипотеза прочности

Гипотеза прочности Мора

где коэффициент k представляет собой отношение предельных напряжений при одноосном растяжении и сжатии. Можно принять

III и IV гипотезы применяют для оценки прочности пластичных материалов, а гипотезу Мора – как для пластичных, так и для хрупких.

Краткая теория по сопромату >
Примеры решения задач >

Источник

Относительное изменение объема

Относительные изменения объема При упругой деформации объем большинства материалов увеличивается при растяжении

и уменьшается при сжатии. Только в частных случаях Р,=0,5 (парафин) объем деформации ПРН не изменяется.

В общем случае напряженного состояния относительное изменение объема
Людмила Фирмаль

равно:©=&x + Wu + ez=+s2+E3= УЛ Ф. (3.35 )) Где o — +гг+_gj+К2+К3. Три. −3 Коэффициент объемной деформации (объемный модуль) y. E A-3(1-2ts) Или =4-t a^°-(ф3-36>нормальная составляющая напряжения в относительном изменении объема: 0^. =Х0-Ф-2Gsx

Дж=Х6-Ф-2Ge^;другие формы: о-=2Г(ех-Е); О—а=2Г(сы); АГ-а = 2Г(ГУ-г); (3.38)где X=7р -:-г-п———п -— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — -) Г2^0 2Gez. (3.37) Рис 3.14. Один. И экс+ЕС+£г е ———— ———— Компонент тангенциального напряжения: B^^x y’tyz^^YG>^GX(3.39)

в частном случае линейного напряженного состояния объем материала стержня, подвергнутого растяжению, может быть записан как: K1=Y[1+b(1-2)). Абсолютное изменение объема AV=V f-V = Vs (1-

2|x). Относительное изменение объема вычисляется по формуле: e==- = e(1-2J1). (3.40)) Для изменения площади поперечного сечения: абсолютный AF=-2 / x-p-F; относительный AF-p — =-2 / x. Например. Уменьшите объем стального стержня (E=2 * 105 МПа), рассчитайте сжимающую осевую силу. Стержень имеет два сечения с

различной площадью поперечного сечения(рис. 3.14), I=2 см, P=450 кН и/х=0,3.
Людмила Фирмаль

Решение. Уменьшение объема первой секции Аки=_4F/(1_2I) — —— (1 — 2|x); во втором разделе Р21 Ава=- — — — — (1-2к); 43 полная потеря веса DU=Al/t + LU2=ZR1 — Ми- (1-2C)=-0. 054cm3.

Смотрите также: