Решение задач на углы параллелограмма опирается на свойства параллелограмма.
Сумма двух углов параллелограмма, прилежащих к одной стороне, равны 180º (так как они являются внутренними односторонними при параллельных прямых (противолежащих сторонах параллелограмма) и секущей (пересекающей их стороне).
Противоположные углы параллелограмма равны.
Поэтому, если в задаче дана сумма углов параллелограмма (не 180º ), то речь идет о его противолежащих углах.
Если сказано, что один из углов параллелограмма больше или меньше другого на некоторое количество градусов (или в несколько раз, или углы относятся в некотором отношении), то речь идет об углах, прилежащих к одной стороне параллелограмма.
Если в задаче требуется найти все углы параллелограмма, в начале изучения темы ищут все четыре угла.
В дальнейшем обычно находят только два из них (прилежащие к одной стороне), поскольку другие два им равны.
Рассмотрим некоторые задачи на нахождение углов параллелограмма.
Задача 1.
Найти углы параллелограмма, если один из его углов на 40º больше другого.
Дано: ABCD — параллелограмм,
∠B на 40º больше ∠A.
Найти: ∠A, ∠B, ∠C,∠D.
Решение:
Пусть ∠A=хº, тогда ∠B=х+40º.
Так как противоположные стороны параллелограмма параллельны, то
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).
Имеем уравнение:
х+х+40=180
2х=180-40
2х=140
х=70
Значит, ∠A=70º, тогда ∠B=70+40=110º.
∠C=∠A=70º, ∠D=∠B=110º (как противолежащие углы параллелограмма).
Ответ: 70º, 70º, 110º, 110º.
Задача 2.
Найти углы параллелограмма, если два из них относятся как 2:3.
Дано: ABCD — параллелограмм,
∠A:∠B=2:3.
Найти: ∠A, ∠B, ∠C,∠D.
Решение:
Пусть k — коэффициент пропорциональности. Тогда ∠A=2kº, ∠B=3kº.
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).
Составим уравнение и решим его:
2k+3k=180
5k=180
k=36
Значит, ∠A=2∙36=72º, ∠B=3∙36=108º.
∠C=∠A=72º, ∠D=∠B=108º (как противолежащие углы параллелограмма).
Ответ: 72º, 72º, 108º, 108º.
Задача 3.
Найти углы параллелограмма, если сумма двух из них равна 150º.
Дано: ABCD — параллелограмм,
∠A+∠C=150º.
Найти: ∠A, ∠B, ∠C,∠D.
Решение:
∠A=∠C=150:2=75º (как противолежащие углы параллелограмма).
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).
Следовательно, ∠B=180º-∠A=180-75=105º.
∠D=∠B=105º (как противолежащие углы параллелограмма).
Ответ: 75º, 75º, 105º, 105º.
На чтение 3 мин. Просмотров 23.4k.
Задача 1. Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.
Решение.
∠C =∠A = 65° как противоположные углы параллелограмма.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.
∠В = 180° — ∠А = 180° — 65° = 115°.
∠D =∠B = 115° как противолежащие углы параллелограмма.
Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.
Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.
Решение.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.
Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.
Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.
Решение.
Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.
х + 3х = 180;
4х = 180;
х = 180 : 4;
х = 45.
Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.
Противолежащие углы параллелограмма равны, следовательно,
∠А =∠С = 45°; ∠В =∠D = 135°.
Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.
Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.
Доказательство.
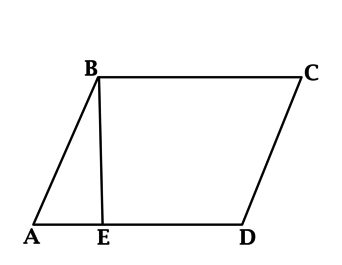
Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.
AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.
Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.
Решение.
Периметр параллелограмма PABCD= 2 ∙ (AB + AD).
Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:
2 ∙ (2x + 5x) = 3,5;
2 ∙ 7x = 3,5;
14x = 3,5;
x = 3,5 : 14;
x = 0,25.
Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Проверка.
Периметр параллелограмма PABCD= 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).
Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.
Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Свойство противолежащих сторон и углов параллелограмма
Свойство противолежащих сторон и углов параллелограмма
Теорема 6.3. У параллелограмма противолежащие сто роны равны, противолежащие углы равны.
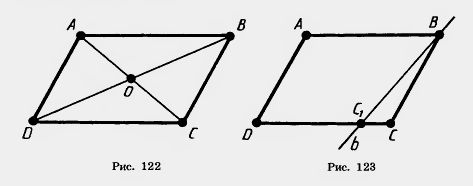
Доказательство. Пусть ABCD — данный параллелограмм (рис. 122). Проведем диагонали параллелограмма. Пусть О — точка их пересечения.
Равенство противолежащих сторон АВ и CD следует из равенства треугольников АОВ и COD. У них углы при вершине О равны как вертикальные, а ОА = ОС и OB—OD по свойству диагоналей параллелограмма. Точно так же из равенства треугольников AOD и СОВ следует равенство другой пары противолежащих сторон — AD и ВС.
Равенство противолежащих углов ABC и CDA следует из равенства треугольников ABC и CD А (по трем сторонам). У них AB=CD и BC=DA по доказанному, а сторона АС общая. Точно так же равенство противолежащих углов BCD и DAB следует из равенства треугольников BCD и DAB. Теорема доказана полностью.
Задача (18). Докажите, что если у четырехугольника две стороны параллельны и равны, то он является параллелограммом.
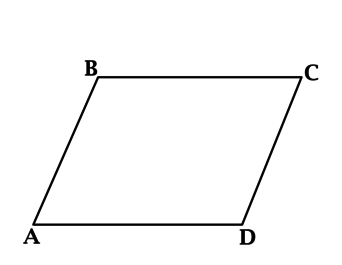
Решение. Пусть ABCD — данный четырехугольник, у которого стороны АВ и CD параллельны и равны (рис. 123). Проведем через вершину В прямую b, параллельную стороне AD. Эта прямая пересекает луч DC в некоторой точке С1. Четырехугольник ABC1D есть параллелограмм. Так как у параллелограмма противолежащие стороны равны, то C1D=AB. А по условию АВ = =CD. Значит, DC=DC1. Отсюда следует, что точки С и C1 совпадают.
Таким образом, четырехугольник ABCD совпадает с параллелограммом ABC1D, а значит, является параллелограммом.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
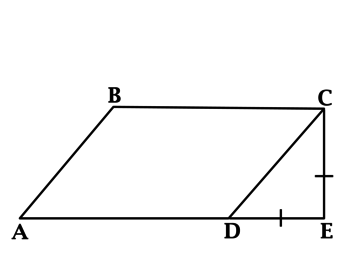
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни