Как найти отношение высот в подобных треугольниках

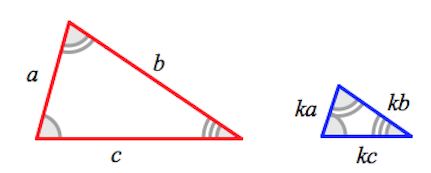
Подобные треугольники

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Примеры наиболее часто встречающихся подобных треугольников

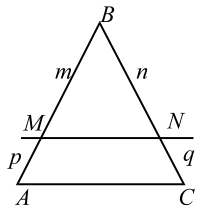
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

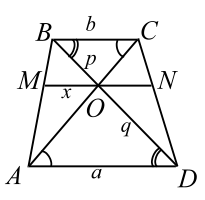
2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

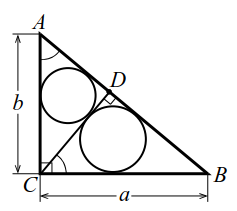
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Отношение высот подобных треугольников

Признака подобия треугольников

Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F

F’`. Напомним, что запись подобия треугольников `Delta ABC

Delta A_1 B_1 C_1` означает, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. `A` переходит в `A_1`, `B` — в `B_1`, `C` — в `C_1`.

Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC

Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,

`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.

Два треугольника подобны, если:

1. два угла одного соответственно равны двум углам другого;

2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;

3. три стороны одного треугольника пропорциональны трём сторонам другого.

В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.

Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.

Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.

И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.

Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.

1. Пусть `O` — точка пересечения диагоналей, `AD = a`, `BC = b`. Прямая `MN` параллельна основанию `AD` (рис. 10а), следовательно, $$ MOparallel AD$$, треугольники `BMO` и `BAD` подобны, поэтому

2. $$ ADparallel BC$$, `Delta AOD

Delta COB` по двум углам (рис. 10б):

`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.

3. Учитывая, что `BD = BO + OD` находим отношение

`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.

Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.

Точки `M` и `N` лежат на боковых сторонах `AB` и `CD` трапеции `ABCD` и $$ MNparallel AD$$ (рис. 11а). Найти длину `MN`, если `BC = a`, `AD = 5a`, `AM : MB = 1:3`.

1. Пусть $$ BFVert CD$$ и $$ MEVert CD$$ (рис. 11б), тогда `/_ 1 = /_ 2`, `/_ 3 = /_ 4` (как соответствующие углы при пересечении двух параллельных прямых третьей) и `Delta AME

Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.

2. Обозначим `MN = x`. По построению `BCNF` и `MNDE` — параллелограммы, `FN = a`, `ED = x` и, значит, `MF = x — a`; `AE = 5a — x`. Итак, имеем `(5a — x)/(x — a) = 1/3`, откуда находим `x = 4a`.

Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.

Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.

Попытайтесь доказать это самостоятельно.

Прямоугольные треугольники подобны, если:

1. они имеют по равному острому углу;

2. катеты одного треугольника пропорциональны катетам другого;

3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.

Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.

Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.

СВОЙСТВА ВЫСОТ И БИССЕКТРИС

Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` — его высоты, то `Delta A_1B_1C

Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).

Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).

В треугольнике `A A_1C` угол `A_1` — прямой, `A_1C = AC cos C = ul (b cos C)`.

В треугольнике `B B_1C` угол `B_1` — прямой, `B_1C = BC cos C = ul (a cos C)`.

В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.

Таким образом, `Delta A_1 B_1 C

Delta ABC` с коэффициентом подобия `ul (cos C)`. (Заметим, что `/_ A_1 B_1 C = /_B`).
б) Треугольник `ABC` — тупоугольный (рис. 12б), угол `C` — острый, высота `A A_1` проведена из вершины тупого угла.

$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cos C =b cos C;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cos C =a cos C,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC,$$

коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.

Случай, когда угол `B` тупой, рассматривается аналогично.
в) Треугольник `ABC` — тупоугольный (рис. 12в), угол `C` — тупой, высоты `A A_1` и `B B_1` проведены из вершин острых углов.

`varphi = /_ BCB_1 = /_ ACA_1 = 180^@ — /_ C`, `cos varphi = — cos C = |cos C|`.

$$left.begin
Delta AA_1C, angle A_1 =90^circ Rightarrow A_1C=ACcdot cosvarphi =b |cos C|;\
Delta BB_1C, angle B_1 =90^circ Rightarrow B_1C=BCcdot cosvarphi =b |cos C|,
end
right>Rightarrow Delta A_1B_1Csim Delta ABC$$

с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.

В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).

Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).

Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).

По первой лемме о высотах `Delta A_1 B_1 C

Delta ABC`, `/_ A_1 B_1 C = /_ B`.

Аналогично `Delta AB_1C_1

Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.

Так как `BB_1` — высота, то `/_AB_1B = /_CB_1B = 90^@`.

Поэтому `/_C_1B_1B = /_A_1B_1B = 90^@ — /_B`, т. е. луч `B_1B` — биссектриса угла `A_1B_1C_1`.

Аналогично доказывается, что `A A_1` — биссектриса угла `B_1 A_1 C_1` и `C_1C` — биссектриса угла `B_1 C_1 A_1`.

Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.

Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.

Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.

1. По условию пересекаются высоты, поэтому треугольник остроугольный. Положим `BH = HB_1 = x` и `HA_1 = y`, тогда `AH = 2y`. По второй лемме о высотах `AH * HA_1 = BH * HB_1`, т. е. `x^2 = 2y^2`, `x = y sqrt 2`.
2. В треугольнике `AHB_1` угол `AHB_1` равен углу `C` (т. к. угол `A_1 AC` равен `90^@ — C`), поэтому `cos C = cos (/_ AHB_1) = x/(2y) = sqrt 2/ 2`. Угол `C` — острый, `/_ C = 45^@`.

Установим ещё одно свойство биссектрисы угла треугольника.

Биссектриса внутреннего угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если `AD` — биссектриса треугольника `ABC`, то `(BD)/(DC) = (AB)/(AC)`.

Проведём через точку `B` прямую параллельно биссектрисе `DA`, пусть `K` — её точка пересечения с прямой `AC` (рис. 16).

Параллельные прямые `AD` и `KB` пересечены прямой `KC`, образуются равные углы `1` и `3`. Те же прямые пересечены и прямой `AB`, здесь равные накрест лежащие углы `2` и `4`. Но `AD` — биссектриса, `/_1 = /_2`, следовательно `/_3 = /_4`. Отсюда следует, что треугольник `KAB` равнобедренный, `KA = AB`.
По теореме о пересечении сторон угла параллельными прямыми из $$ ADVert KB$$ следует `(BD)/(DC) = (KA)/(AC)`. Подставляя сюда вместо `KA` равный ему отрезок `AB`, получим `(BD)/(DC) = (AB)/(AC)`. Теорема доказана.

Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.

Пусть `AD` — биссектриса и `BD = 3`, `DC = 5` (рис. 17).

По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.

Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16

Подобные треугольники

Два треугольника подобны, если об этом сказано в условии либо если это можно доказать по одному из признаков подобия треугольников.

Подобные треугольники — это треугольники, у которых углы равны, а стороны пропорциональны.

Два треугольника подобны, если между их точками можно установить взаимно-однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек равно одной и той же постоянной k, k — коэффициент подобия).

Как и в случае равных треугольников, важно правильно называть подобные треугольники: равные углы должны находиться на соответствующих позициях.

Определение подобных треугольников предполагает выполнение шести пар равенств (равенство трёх пар углов и пропорциональность трёх пар сторон). Признаки подобия позволяют сократить число равенств до 2-3 (для прямоугольных треугольников — до 1-2).

Свойства подобных треугольников

1) Периметры подобных треугольников относятся как их соответствующие стороны:

2) Соответствующие линейные элементы подобных треугольников (медианы, высоты, биссектрисы и т.д.) относятся как их соответствующие стороны.

3) Площади подобных фигур относятся как квадраты их соответствующих линейных размеров:

Подобные треугольники

3 октября 2022

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Подобные треугольники — ключевая тема геометрии 8 класса. Они будут преследовать нас до самого конца школы. И сегодня мы разберём всё, что нужно знать о них.

План такой:

1. Основное определение
2. Лемма о подобных треугольниках
3. Свойства подобных треугольников
4. Разбор задач

1. Основное определение

Определение. Треугольники называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Рассмотрим треугольники $ABC$ и $MNK$:

У них есть равные углы: $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. И пропорциональные стороны:

[frac{AB}{MN}=frac{BC}{NK}= frac{AC}{MK}= frac{color{red}{3}}{color{red}{2}}]

Следовательно, треугольники $ABC$ и $MNK$ подобны. Записывается это так:

[Delta ABCsim Delta MNK]

Число $k={color{red}{3}}/{color{red}{2}};$ называется коэффициентом подобия. К нему мы ещё вернёмся.

Пропорциональные стороны подобных треугольников (например, $AB$ и $MN$, либо $BC$ и $NK$) в некоторых учебниках называют сходственными. На практике этот термин применяется редко. Мы будем говорить просто «соответственные стороны».

Дальше идёт очень важное замечание.

1.1. Обозначение подобных треугольников

В геометрии один и тот же треугольник можно называть по-разному. Например, $Delta ABC$, $Delta BCA$ или $Delta CAB$ — это всё один и тот же треугольник. То же самое касается и углов.

Но в подобных треугольниках есть негласное правило:

При обозначении подобных треугольников порядок букв выбирают так, чтобы равные углы перечислялись в одной и той же последовательности.

Вернёмся к нашим треугольникам $ABC$ и $MNK$:

Поскольку $anglecolor{red}{A}=anglecolor{red}{M}$ и $anglecolor{blue}{B}=anglecolor{blue}{N}$, можно записать $Deltacolor{red}{A}color{blue}{B}Csim Deltacolor{red}{M}color{blue}{N}K$. Или $Delta Ccolor{red}{A}color{blue}{B}sim Delta Kcolor{red}{M}color{blue}{N}$. Но никак не $Deltacolor{red}{A}color{blue}{B}Csim Delta Kcolor{red}{M}color{blue}{N}$.

Да, это негласное правило. И если вы нарушите последовательность букв, это не ошибка. Никто не снизит вам за это баллы. А если снизит — добро пожаловать на апелляцию.

Правильная запись позволяет быстро и безошибочно выписывать пропорциональные стороны треугольников. Рассмотрим два подобных треугольника:

[Delta ABCsim Delta MNK]

Берём две первые буквы из каждого треугольника: ${AB}/{MN};$. Затем две последние буквы: ${BC}/{NK};$. Наконец, вычёркиваем «центральную» букву: ${AC}/{MK};$.

Приравниваем полученные три дроби:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Вот и всё! Даже рисунок не нужен! Этот приём настолько прост и эффективен, что его в обязательном порядке изучают на моих занятиях, курсах и вебинарах.

В будущем мы увидим, что подобные треугольники чаще всего ищут как раз для составления таких пропорций.

2. Лемма о подобных треугольниках

Подобные треугольники появляются всякий раз, когда прямая, параллельная стороне треугольника, пересекает его стороны.

Теорема 1. Прямая, пересекающая две стороны треугольника и параллельная третьей стороне, отсекает треугольник, подобный исходному.

Доказательство. Рассмотрим треугольник $ABC$. Пусть прямая $MNparallel AB$ отсекает треугольник $MNC$:

Докажем, что $Delta ABCsim Delta MNC$. Рассмотрим треугольники $ABC$ и $MNC$. У них есть общий угол $ACB$.

Углы $ABC$ и $MNC$ — соответственными при $MNparallel AB$ и секущей $BC$. Следовательно, они равны: $angle ABC=angle MNC$.

Аналогично равны углы $BAC$ и $NMC$. Следовательно, треугольники $ABC$ и $MNC$ имеют три соответственно равных угла.

Докажем теперь, что соответственные стороны пропорциональны. Т.е. докажем пропорцию

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Рассмотрим угол $ACB$. Параллельные прямые $AB$ и $MN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AC}{MC}=frac{BC}{NC}]

Это равенство — второе в искомом:

[frac{AB}{MN}= color{red}{frac{BC}{NC}=frac{AC}{MC}}]

Осталось доказать первое равенство. Дополнительное построение: прямая $KNparallel AC$:

Поскольку $AMparallel KN$ (по построению) и $AKparallel MN$ (по условию), четырёхугольник $AKNM$ — параллелограмм. Поэтому $AK=MN$.

Рассмотрим угол $ABC$. Параллельные прямые $AC$ и $KN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AB}{AK}=frac{BC}{NC}]

Учитывая, что $AK=MN$, получаем

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Итак, соответственные углы треугольников $ABC$ и $MNC$ равны, а их стороны пропорциональны. Следовательно, по определению подобных треугольников

[Delta ABCsim Delta MNC]

Что и требовалось доказать.

Эта лемма — не признак подобия. Это самостоятельная теорема, которая ускоряет решение многих задач.

Признаки подобия разобраны в отдельном уроке — см. «Признаки подобия треугольников».

Частный случай этой леммы — средняя линия. Она отсекает треугольник со сторонами в два раза меньше, чем у исходного:

Оформляется это так. Поскольку $AM=MC$ и $BN=NC$, то $MN$ — средняя линия треугольника $ABC$. Следовательно, прямые $AB$ и $MN$ параллельны, откуда

[Delta ABCsim Delta MNC]

3. Свойства подобных треугольников

Два важнейших свойства: связь периметров и связь площадей.

3.1. Периметры подобных треугольников

Теорема 2. Отношение периметров подобных треугольников равно коэффициенту подобия.

Доказательство. Рассмотрим подобные треугольники $ABC$ и $MNK$:

Запишем равенство из определения подобия. Поскольку $Delta ABCsimDelta MNK$, стороны этих треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

Здесь число $color{red}{k}$ — коэффициент подобия. Полученное тройное равенство можно переписать так:

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}; frac{AC}{MK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB&=color{red}{k}cdot MN \ BC &=color{red}{k}cdot NK \ AC &=color{red}{k}cdot MK \ end{align}]

Периметр треугольника $MNK$:

[{{P}_{Delta MNK}}=MN+NK+MK]

Периметр треугольника $ABC$:

[begin{align}{{P}_{Delta ABC}} &=AB+BC+CD= \ &=color{red}{k}cdot MN+color{red}{k}cdot NK+color{red}{k}cdot MK= \ &=color{red}{k}cdot left( MN+NK+MK right)= \ &=color{red}{k}cdot {{P}_{Delta MNK}} end{align}]

Итого получаем равенство

[{{P}_{Delta ABC}}=color{red}{k}cdot {{P}_{Delta MNK}}]

Обычно именно в таком виде это равенство и применяют. Но можно записать его и как отношение:

[frac{{{P}_{Delta ABC}}}{{{P}_{Delta MNK}}}=color{red}{k}]

В любом случае, мы получили отношение, которое и требовалось доказать.

3.2. Площади подобных треугольников

Теорема 3. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство. Первые шаги очень похожи на доказательство предыдущей теоремы. Вновь рассмотрим подобные треугольники $ABC$ и $MNK$:

Поскольку $Delta ABCsimDelta MNK$, углы $ABC$ и $MNK$ равны. Следовательно, равны синусы этих углов:

[begin{align}angle ABC &=angle MNK=color{blue}{alpha} \ sin angle ABC &=sin angle MNK=sin color{blue}{alpha} end{align}]

Кроме того, стороны подобных треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

В частности, из этого равенства следует, что

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB &= color{red}{k}cdot MN \ BC &= color{red}{k}cdot NK \ end{align}]

Площадь треугольника $MNK$:

[{{S}_{Delta MNK}}=frac{1}{2}cdot MNcdot NKcdot sin color{blue}{alpha} ]

Площадь треугольника $ABC$:

[begin{align}{{S}_{Delta ABC}} &=frac{1}{2}cdot ABcdot BCcdot sincolor{blue}{alpha} = \ &=frac{1}{2}cdotcolor{red}{k}cdot MNcdotcolor{red}{k}cdot NKcdot sincolor{blue}{alpha} = \ &={color{red}{k}^{2}}cdot frac{1}{2}cdot MNcdot NKcdot sin alpha = \ &={color{red}{k}^{2}}cdot {{S}_{Delta MNK}} end{align}]

Получаем равенство

[{{S}_{Delta ABC}}={color{red}{k}^{2}}cdot {{S}_{Delta MNK}}]

Перепишем в виде отношения:

[frac{{{S}_{Delta ABC}}}{{{S}_{Delta MNK}}}={color{red}{k}^{2}}]

Что и требовалось доказать.

Для доказательства теоремы мы использовали формулу площади треугольника:

[{{S}_{Delta }}=frac{1}{2}absin alpha ]

Тригонометрию проходят после подобия, поэтому мы опираемся на ещё не изученный материал.

Впрочем, ничто не мешает взять уже известную формулу:

[{{S}_{Delta }}=frac{1}{2}ah]

Здесь $a$ — сторона треугольника, $h$ — высота, проведённая к этой стороне. Дело в том, что высоты в подобных треугольниках тоже пропорциональны. И не только высоты. Назовём это Свойством 3.3.:)

3.3. Элементы подобных треугольников

Теорема 4. Отношение высот, биссектрис и медиан, проведённых к соответствующим сторонам подобных треугольников, равно коэффициенту подобия.

Проиллюстрируем это на высотах. Пусть треугольники $ABC$ и $MNK$ подобны:

В этом случае высоты $CDbot AB$ и $KLbot MN$ относятся как

[frac{CD}{KL}=frac{AB}{MN}= color{red}{k}]

Для доказательства этой теоремы нужно знать признаки подобия. Поэтому оставим его до следующего урока. А сейчас переходим к задачам.

4. Задачи на подобие

Здесь разобрано пять задач на подобие треугольников. Все они довольно простые. За сложными задачами добро пожаловать в задачник.:)

Задача 1. Готовые треугольники

Известно, что треугольники $ABC$ и $MNK$ подобны, причём $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. Кроме того, стороны $AB=6$, $BC=7$, $AC=10$ и $MN=9$. Найдите стороны $NK$ и $MK$.

Решение. Построим треугольники $ABC$ и $MNK$, отметим известные стороны:

Из условия $Delta ABCsim Delta MNK$ следует, что верно равенство

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Подставим в это равенство всё, что нам известно:

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}=frac{color{red}{10}}{MK}]

Опустим последнюю дробь и получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}]

Найдём сторону $NK$:

[NK=frac{color{red}{9}cdot color{red}{7}}{color{red}{6}}=10,5]

Аналогично, убирая среднюю дробь, получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{10}}{MK}]

Найдём сторону $MK$:

[NK=frac{color{red}{9}cdot color{red}{10}}{color{red}{6}}=15]

Ответ: $NK=10,5$, $MK=15$.

Задача 2. Прямая, параллельная стороне

Прямая, параллельная стороне $AC$ треугольника $ABC$, пересекает сторону $AB$ в точке $D$, а сторону $BC$ — в точке $E$. Найдите:

а) Отрезок $BD$, если $AB=16$, $AC=20$, $DE=15$.

б) Отрезок $AD$, если $AB=28$, $BC=63$, $BE=27$.

Решение. Для начала построим рисунок. Он будет общий для обоих пунктов.

Из условия следует, что прямая $DE$ пересекает стороны треугольника $ABC$:

Поскольку $DEparallel AC$, по лемме о подобных треугольниках прямая $DE$ отсекает от треугольника $ABC$ новый треугольник, подобный исходному:

[Delta ABCsim Delta DBE]

Из подобия треугольников $ABC$ и $DBE$ следует равенство

[frac{AB}{DB}=frac{BC}{BE}=frac{AC}{DE}]

Решаем пункт а). Подставляем в это равенство всё, что нам известно:

[frac{color{red}{16}}{DB}=frac{BC}{BE}=frac{color{red}{20}}{color{red}{15}}]

Вычёркиваем среднюю дробь и получаем пропорцию

[frac{color{red}{16}}{DB}=frac{color{red}{20}}{color{red}{15}}]

Отсюда легко найти $DB$ (или, что то же самое, $BD$):

[DB=frac{color{red}{16}cdotcolor{red}{15}}{color{red}{20}}=12]

Аналогично решаем пункт б). Подставляем в исходное равенство известные величины:

[frac{color{red}{28}}{DB}=frac{color{red}{63}}{color{red}{27}}=frac{AC}{DE}]

Первые две дроби образуют пропорцию, из которой вновь легко найти $DB$:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=12]

Осталось найти $AD$:

[begin{align}AD &=AB-BD= \ &=color{red}{28}-color{red}{12}=16 end{align}]

Ответ: а) $BD=12$; б) $AD=16$.

Важное замечание по работе с пропорциями. Ни в коем случае не нужно перемножать числа в числителе.

Напротив: нужно разложить их на множители и сократить!

Взгляните:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=frac{4cdotcolor{blue}{7}cdot 3cdotcolor{green}{9}}{color{blue}{7}cdotcolor{green}{9}}=12]

Так вы сэкономите время, избежите умножения столбиком и защитите себя от множества ошибок. Никогда не умножайте большие числа, если дальше их нужно будет сокращать.

Задача 3. Доказательство подобия

Точки $M$ и $K$ — середины сторон $CD$ и $AD$ квадрата $ABCD$ соответственно. Докажите, что треугольники $MDK$ и $BCD$ подобны.

Решение. Сделаем первоначальный рисунок по условию задачи:

Здесь нет прямых, параллельных сторонам треугольника, поэтому лемма о подобных треугольниках не поможет. Докажем подобие по определению.

Сначала разберёмся с углами. Поскольку $ABCD$ — квадрат, и $KD=MD$ — половина стороны квадрата, треугольники $MDK$ и $BCD$ — прямоугольные и равнобедренные.

Все острые углы треугольников $MDK$ и $BCD$ равны 45°. Можем записать это так:

[begin{align}angle BCD &=angle MDK={90}^circ \ angle CBD &=angle DMK={45}^circ \ angle CDB &=angle DKM={45}^circ \ end{align}]

Дополнительное построение: диагональ квадрата $color{red}{AC}$:

Рассмотрим треугольник $ACD$. Отрезок $KM$ — средняя линия, поэтому $KM={color{red}{AC}}/{2};$. С другой стороны, $AC=BD$ как диагонали квадрата. Поэтому верно равенство

[frac{KM}{BD}=frac{KM}{color{red}{AC}}=frac{1}{2}]

Но тогда выполняется следующее равенство:

[frac{MD}{BC}=frac{DK}{CD}=frac{MK}{BD}=frac{1}{2}]

А это вместе с равенством углов как раз и означает, что треугольники $MDK$ и $BCD$ подобны:

[Delta MDKsim Delta BCD]

Доказательство завершено.

Мы доказали подобие треугольников по определению. Если пользоваться признаками подобия, всё будет намного быстрее. Но пока мы не вправе пользоваться этими признаками.

Задача 4. Вписанный ромб

В треугольник $ABC$ вписан ромб $BDEK$ так, как показано на рисунке. Найдите сторону ромба, если $AB=10$, $BC=15$.

Решение. Пусть искомая сторона ромба равна $color{red}{x}$. Из условия задачи получим такой рисунок:

Зная, что $AB=10$ и $BC=15$, выразим $AK$ и $CD$:

[begin{align}AK &=10-color{red}{x} \ CD &=15-color{red}{x} \ end{align}]

Далее рассмотрим треугольник $ABC$. Поскольку $BDEK$ — ромб, то $KEparallel BC$. По лемме о подобных треугольниках имеем:

[Delta ABCsim Delta AKE]

В подобных треугольниках подобные стороны пропорциональны, поэтому

[frac{AB}{AK}=frac{BC}{KE}=frac{AC}{AE}]

Подставим в это равенство всё, что нам известно или выражено через $color{red}{x}$:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}=frac{AC}{AE}]

Последняя дробь оказалась бесполезной. Вычеркнем её и получим пропорцию:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}]

Применяем основное свойство пропорции и уравнение:

[begin{align}10cdotcolor{red}{x} &=15cdot left( 10- color{red}{x} right) \ 2cdotcolor{red}{x} &=3cdot left( 10- color{red}{x} right) \ &cdots\ color{red}{x} &=6 end{align}]

Это и есть искомая сторона ромба. Она равна $color{red}{x}=6$.

Ответ: $BD=6$.

Задача 5. Свойства биссектрисы

В треугольнике $ABC$ стороны $AB=8$, $BC=12$, угол $ABC={120}^circ $. Отрезок $BD$ — биссектриса. Найдите длину $BD$.

Решение. Из условия задачи можно сделать вот такой рисунок:

Поскольку $BD$ — биссектриса угла в треугольнике, точка $D$ делит сторону $AC$ на отрезки, пропорциональные сторонам $AB$ и $BC$. Это можно записать так:

[frac{AD}{CD}=frac{AB}{CB}=frac{color{red}{8}}{color{red}{12}}=frac{color{red}{2}}{color{red}{3}}]

Обозначим пропорциональные отрезки переменными. Пусть $AD=color{blue}{2x}$, $CD=color{blue}{3x}$.

Дополнительное построение: прямая $DMparallel AB$:

Рассмотрим угол $ACB$. Поскольку $DMparallel AB$, по теореме о пропорциональных отрезках получаем, что

[frac{BM}{CM}=frac{AD}{CD}=frac{color{red}{2}}{color{red}{3}}]

Вновь обозначим пропорциональные отрезки переменными. Пусть $BM=color{blue}{2y}$, $CM=color{blue}{3y}$. Но тогда

[BC=BM+MC=color{blue}{5y}=color{red}{12}]

Получаем, что $color{blue}{y}=color{red}{2,4}$. Отсюда легко найти длину $BM$:

[BM=color{blue}{2y}=2cdotcolor{red}{2,4}= color{red}{4,8}]

Далее заметим, что если угол $ABC$ равен 120°, то

[angle ABD=angle CBD={60}^circ ]

С другой стороны, прямые $AB$ и $MD$ параллельны по построению. Прямая $BD$ — секущая для этих параллельных прямых.

Следовательно, углы $ABD$ и $BDM$ — внутренние накрест лежащие, поэтому

[angle BDM=angle ABD={60}^circ ]

Рассмотрим треугольник $BDM$. В нём есть два угла по 60°. Следовательно, это равносторонний треугольник:

[BD=BM=color{red}{4,8}]

Мы нашли длину отрезка $BD$. Задача решена.

Ответ: $BD=4,8$.

Итак, с определением разобрались. В следующем уроке разберём признаки подобия.:)

Смотрите также:

1. Как применяется теорема косинусов и подобие треугольников для решения широкого класса задач в планиметрии.
2. Теорема менелая
3. Комбинаторика в задаче B6: легкий тест
4. Введение системы координат
5. Четырехугольная пирамида: как найти координаты вершин
6. Нестандартная задача B5 на площадь круга

Текст

Рисунок,
чертеж

Комментарий

Отношением отрезков AB и CD называется
отношение их длин.

=;

Отрезки AB и CD пропорциональ-

ны  отрезкам
A₁B₁ и C₁D₁, если

Теорема о свойстве биссектрисы
треугольника: биссектриса треугольника делит
противоположную сторону на отрезки, пропорциональные прилежащим сторонам
треугольника. (№535)

Два треугольника
называются подобными, если их углы соответственно равны и
стороны одного треугольника пропорциональны сходственным сторонам другого.

A=A₁; В=В₁; С=С₁;

(коэффициент подобия)

Сходственные стороны – стороны, лежащие против равных углов в
подобных треугольниках.

AB
— A₁B₁;

BC
— B₁C₁;

AC
— A₁C₁;

Коэффициент подобия – число, равное отношению сходственных
сторон подобных треугольников.

(коэффициент подобия)

Теорема об отношении площадей
подобных треугольников: отношение площадей двух подобных
треугольников равно квадрату коэффициента подобия.

ΔNDK ~ ΔCMR;

S₁
: S₂ = k²;

Теорема об отношении высот,
проведённых к сходственным сторонам в подобных треугольниках: отношение сходственных сторон подобных треугольников равно отношению
высот, проведённым к этим сторонам;

или

отношение высот, проведённых к сходственным сторонам
подобных треугольников, равно коэффициенту подобия. (№543)

;

;

Теорема об отношении периметров
двух подобных треугольников: отношение
периметров двух подобных треугольников равно коэффициенту подобия. (№547)

рис. см. выше;

ΔАВС ~ Δ А₁В₁С₁;

P : P₁=k;

ПРИЗНАКИ   ПОДОБИЯ   ТРЕУГОЛЬНИКОВ

I признак: если два угла одного треугольника
соответственно равны двум углам другого, то такие треугольники подобны.

A=A₁; В=В₁;

II
признак: если две
стороны одного треугольника пропорциональны двум сторонам другого треугольника
и углы, заключённые между этими сторонами, равны, то такие треугольники
подобны.

; A=A₁;

III признак: если три стороны одного треугольника
пропорциональны трём сторонам другого треугольника, то такие треугольники
подобны.

;

Теорема о свойстве параллельных
прямых, пересекающих стороны угла (более общая формулировка теоремы
Фалеса): параллельные прямые, пересекающие стороны
угла, отсекают на сторонах угла пропорциональные отрезки. (№556; №558)

=;

=;

Средней линией треугольника называется отрезок, соединяющий середины
двух его сторон.

Теорема о средней линии треугольника: средняя линия треугольника параллельна одной из его сторон и равна
половине этой стороны.

MN – средняя линия треугольника;

MN | | AC;

MN=
½AC;

Средней линией трапеции называется отрезок, соединяющий середины
боковых сторон трапеции.

Теорема о средней линии трапеции: средняя линия трапеции параллельна основаниям и равна их полусумме.

QP – средняя линия трапеции;

BC | | QP | | AD;

QP=½ (BC+AD);

Теорема: середины сторон произвольного четырёхугольника являются вершинами параллелограмма. (№567)

KMNF
— параллелограмм

Теорема о медианах треугольника: медианы треугольника пересекаются в одной точке, которая делит каждую
медиану в отношении 2:1, считая от вершины.

Теорема: отрезок, соединяющий середины диагоналей
трапеции, параллелен её основаниям и равен полуразности оснований. (№569)

BC
| | MN | | AD;

MN=½ (AD- BC);

ПРОПОРЦИОНАЛЬНЫЕ  ОТРЕЗКИ  В  ПРЯМОУГОЛЬНОМ 
ТРЕУГОЛЬНИКЕ

Отрезок XY называется
средним пропорциональным (или средним
геометрическим) для отрезков AB
CD, если XY=;

Теорема: высота прямоугольного треугольника,
проведённая из вершины прямого угла, разделяет треугольник на два
подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Следствие 1.  Высота прямоугольного треугольника, проведённая
из вершины прямого угла,
есть среднее пропорциональное для отрезков, на которые делится гипотенуза
этой высотой.

Следствие 2. Катет прямоугольного треугольника есть среднее пропорциональное для
гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой
из вершины прямого угла.

ADC ~ACB~BDC;

CD=;

AC=;

CB=;

Пропорциональные отрезки в прямоугольном
треугольнике

1.  ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ
ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

Синусом острого угла прямоугольного треугольника называется
отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется
отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется
отношение противолежащего катета к прилежащему.

Тангенс угла равен отношению синуса к косинусу этого угла.

Котангенсом острого угла прямоугольного треугольника называется
отношение прилежащего катета к противолежащему.

Котангенс угла равен отношению косинуса к синусу этого угла.

sin=;

cos=;

tg=;

tg=

ctg=;

ctg=

Основное тригонометрическое тождество

sin²+cos²=1;

Теорема: если острый угол одного прямоугольного треугольника
равен острому углу другого прямоугольного треугольника, то синусы этих углов
равны, косинусы этих углов равны, тангенсы этих углов равны, котангенсы этих
углов равны.

sinA=sinA₁;

cosA=cosA₁;

tgA=tgA₁;

ctgA=ctgA₁;

ЗНАЧЕНИЯ sin, cos, tg, ctg ДЛЯ УГЛОВ 30⁰, 45⁰,
60⁰

§ 1. Подобие треугольников. Отношение площадей подобных треугольников. Свойства медиан, биссектрис и высот

Две фигуры $$ F$$ и $$ {F}^{text{‘}}$$  называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры $$ F$$ и $$ {F}^{text{‘}}$$  подобны, то пишется $$ Fsim {F}^{text{‘}}$$Напомним, что в записи подобия треугольников $$ ∆ABC~∆{A}_{1}{B}_{1}{C}_{1}$$ предполагается, что вершины, совмещаемые преобразованием  подобия, стоят на соответствующих местах, т. е. $$ A$$ переходит в $$ {A}_{1}$$, $$ B$$ — в $$ {B}_{1}$$, $$ C$$ — в $$ {C}_{1}$$. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если $$ ∆ABC~∆{A}_{1}{B}_{1}{C}_{1}$$

$$ angle A=angle {A}_{1}, angle B=angle {B}_{1}, angle C=angle {C}_{1}, {displaystyle frac{AB}{{A}_{1}{B}_{1}}}={displaystyle frac{BC}{{B}_{1}{C}_{1}}}={displaystyle frac{AC}{{A}_{1}{C}_{1}}}$$.

Из признаков подобия следует утверждения, которые удобно использовать в решении задач: 

1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.

Рис. 5

2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам,   т. е. если  $$ MNleft|right|AC$$ (рис. 5), то

$$ {displaystyle frac{m}{n}}={displaystyle frac{p}{q}}=frac{m+p}{n+q}$$

3°. Если  прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)

$$ {displaystyle frac{m}{n}}={displaystyle frac{m+p}{n+q}}$$ или $$ {displaystyle frac{m}{n}}={displaystyle frac{p}{q}}$$,

то $$ MN$$ параллельна $$ AC$$ (доказательство было дано в задании для  9 класса).

Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках $$ M$$ и $$ N$$. Найти длину отрезка `MN`, если  основания  трапеции равны $$ a$$ и $$ b$$.

Пусть $$ O$$ точка пересечения диагоналей трапеции (рис. 6). Обозначим:

$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$

$$1.;left.begin{array}{l}BCparallel AD\bigtriangleup BOCsimbigtriangleup DOA;(mathrm{по};mathrm{двум};mathrm{углам})end{array}right|Rightarrowdfrac ba=dfrac pq$$                                        (1)

$$2.;left.begin{array}{l}MOparallel AD\bigtriangleup MBOsimbigtriangleup ABDend{array}right|Rightarrowdfrac xa=dfrac p{p+q}$$.                                         (2)

Из (1) и (2) следует $$ x=a{displaystyle frac{p}{p+q}}=q{displaystyle frac{p/q}{p/q+1}}={displaystyle frac{ab}{a+b}}$$, т. е. $$ MO={displaystyle frac{ab}{a+b}}.$$

Аналогично устанавливаем, что $$ NO={displaystyle frac{ab}{a+b}}$$, поэтому $$ overline{)MN={displaystyle frac{2ab}{a+b}}}$$.

Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить. 

Рис. 6

Рис. 7

В прямоугольном треугольнике  $$ ABC$$ из вершины $$ C$$ прямого угла проведена высота $$ CD$$ (рис. 7). Радиусы  окружностей, вписанных в треугольники $$ ACD$$ и $$ BCD$$ равны соответственно $$ {r}_{1}$$ и $$ {r}_{2}$$. Найти радиус окружности, вписанной в треугольник $$ ABC$$.

 Обозначим искомый радиус $$ r$$, положим $$ AB=c$$, $$ AC=b$$, $$ BC=a$$. Из подобия прямоугольных треугольников $$ ACD$$ и $$ ABC$$ (у   них   равные углы при вершине $$ A$$) имеем $$ {displaystyle frac{r}{{r}_{1}}}={displaystyle frac{c}{b}}$$, откуда $$ b={displaystyle frac{{r}_{1}}{r}}c$$. Прямоугольные треугольники  $$ BCD$$ и  $$ BAC$$ также  подобны,  поэтому $$ {displaystyle frac{r}{{r}_{2}}}={displaystyle frac{c}{a}}$$, — откуда $$ a={displaystyle frac{{r}_{2}}{r}}c$$. Так как $$ {a}^{2}+{b}^{2}={c}^{2}$$ то, возводя в квадрат выражения для  $$ a$$ и $$ b$$ и складывая их, получим $$ {left(frac{{r}_{1}}{r}right)}^{2}{c}^{2}+{left(frac{{r}_{2}}{r}right)}^{2}{c}^{2}={c}^{2}$$ или $$ {displaystyle frac{{r}_{1}^{2}+{r}_{2}^{2}}{{r}^{2}}}=1$$.  Находим  $$ r=sqrt{{{r}_{1}}^{2}+{{r}_{2}}^{2}}$$. 

Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.

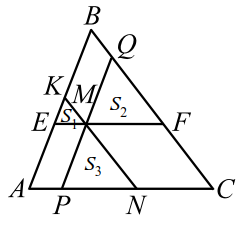Рис. 8

Через точку $$ M$$, лежащую внутри треугольника $$ ABC$$, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны $$ {S}_{1}$$, $$ {S}_{2}$$  и $$ {S}_{3}$$. Найти  площадь треугольника $$ ABC$$.

Легко видеть, что треугольники $$ EKM$$, $$ MQF$$ и $$ PMN$$ подобны треугольнику $$ ABC$$.

Пусть $$ S$$ -площадь треугольника $$ ABC$$, тогда

$$ {displaystyle frac{{S}_{1}}{S}}={left({displaystyle frac{EM}{AC}}right)}^{2}; {displaystyle frac{{S}_{2}}{S}}={left({displaystyle frac{MF}{AC}}right)}^{2}; {displaystyle frac{{S}_{3}}{S}}={left({displaystyle frac{PN}{AC}}right)}^{2}.$$

Откуда находим

$$ EM=sqrt{{displaystyle frac{{S}_{1}}{S}}}AC, MF=sqrt{{displaystyle frac{{S}_{2}}{S}}}AC, PN=sqrt{{displaystyle frac{{S}_{3}}{S}}}AC.$$

А так как $$ EM=AP, MF=NC$$, то $$ EM+PN+MF=AP+PN+NC=AC$$.

Таким образом, $$ AC=AC·left(sqrt{{displaystyle frac{{S}_{1}}{S}}}+sqrt{{displaystyle frac{{S}_{2}}{S}}}+sqrt{{displaystyle frac{{S}_{3}}{S}}}right)$$, откуда следует

$$ S={left(sqrt{{S}_{1}}+sqrt{{S}_{2}}+sqrt{{S}_{3}}right)}^{2}$$.

Свойства медиан, высот, биссектрис треугольника

В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них  мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.

Рис. 9

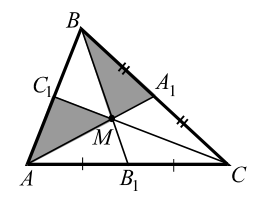
Теорема 1. Три медианы треугольника пересекаются в одной точке  и  точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.

Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.

(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна $$ {displaystyle frac{1}{2}}{S}_{ABC}$$. Точка пересечения медиан называется центром тяжести треугольника. 

Теорема 3. Пусть $$ BD$$ — медиана треугольника 

$$ ABC (BC=a, AC=b, AB=c, BD={m}_{a})$$, тогда

$$ {m}_{c}^{2}={displaystyle frac{{a}^{2}+{b}^{2}}{2}}-{displaystyle frac{{c}^{2}}{4}}$$. (Доказательство приведено далее в §4 Задания).

Рис. 10

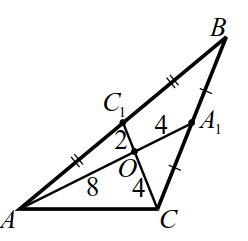
Медианы $$ A{A}_{1}$$ треугольника $$ ABC$$ пересекаются в точке $$ O$$, $$ A{A}_{1}=12$$ и $$ C{C}_{1}=6$$ и одна из сторон треугольника равна `12`. (рис. 10). Найти площадь треугольника  $$ ABC$$.

1. По теореме 1 имеем  $$ AO={displaystyle frac{2}{3}}A{A}_{1}=8$$, $$ CO={displaystyle frac{2}{3}}C{C}_{1}=4$$. 

Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона $$ AC$$ не может равняться `12`, иначе $$ AC=AO+OC$$ — нарушено неравенство треугольника. Также не может равняться `12` сторона $$ AB$$, так в этом случае $$ A{C}_{1}=6$$ и треугольник $$ AO{C}_{1}$$  со сторонами `8`, `2`, `6` не существует. Значит,  $$ BC=12$$ и $$ A{C}_{1}=6$$.

2. Площадь треугольника находим по формуле Герона:

$$ p=7, {S}_{{A}_{1}OC}=sqrt{7·1·3·3}=3sqrt{7}$$.

По теореме 2 площадь треугольника  $$ ABC$$ в `6` раз больше, находим $$ {S}_{ABC}=18sqrt{7}$$.

Рис. 13

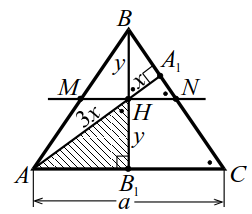
Высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ пересекаются в точке $$ H$$ (рис. 13), при этом $$ AH=3H{A}_{1}$$ и $$ BH=H{B}_{1}$$. Найти косинус угла $$ ACB$$ и площадь треугольника $$ ABC$$, если $$ AC=a$$.  

Обозначим $$ H{A}_{1}=x, H{B}_{1}=y$$, 

1. Точка $$ H$$ — середина высоты (рис. 13). Если отрезок $$ MH$$ проходит через точку $$ H$$ и параллелен  основаниям,  то `MN` — средняя линия; `MN=a/2`.

2. $$left.triangle HA_1Nsimtriangle AA_1Cright|Rightarrowdfrac{HN}{AC}=dfrac x{4x},;HN=dfrac14a.$$ Значит, $$ MH=HN={displaystyle frac{a}{4}}$$ и $$ A{B}_{1}={B}_{1}C={displaystyle frac{a}{2}}$$ Треугольник  $$ ABC$$  равнобедренный, $$ AB=BC$$.

3. $$ angle {B}_{1}BC=90°-angle C$$, поэтому `ul(/_BHA_1=/_AHB_1=/_C)`, а по второй лемме о высотах  $$ AH·H{A}_{1}=BH·H{B}_{1}$$ т. е.  $$ 3{x}^{2}={y}^{2}, y=xsqrt{3}$$.

Далее, $$ mathrm{cos}C=mathrm{cos}(angle AH{B}_{1})={displaystyle frac{y}{3x}}$$, находим $$ mathrm{cos}C={displaystyle frac{1}{sqrt{3}}}$$.

4. $$ △AH{B}_{1}: A{B}_{1}^{2}=(3x{)}^{2}-{y}^{2}$$, $$ {displaystyle frac{{a}^{2}}{4}}=6{x}^{2}$$, $$ x={displaystyle frac{a}{2sqrt{6}}}$$, $$ y={displaystyle frac{a}{2sqrt{2}}}$$, тогда

$$ {S}_{ABC}={displaystyle frac{1}{2}}AC·B{B}_{1}=ay={displaystyle frac{{a}^{2}sqrt{2}}{4}}$$.

22
Авг 2013

Категория: Справочные материалы

Подобные треугольники

2013-08-22
2014-01-31

Автор: egeMax |

комментариев 50