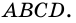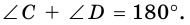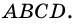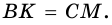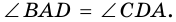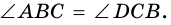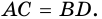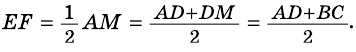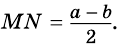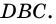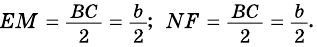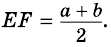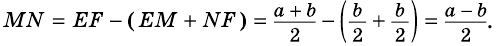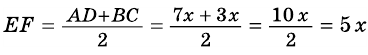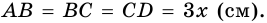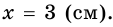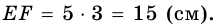25
Июл 2013
Категория: Справочные материалы
Трапеция. Свойства трапеции
2013-07-25
2016-06-15
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Автор: egeMax |
комментарий 431
Печать страницы
Трапеция, ее свойства, формулы площади, высоты, сторон.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция (понятие, определение)
Видеоурок “Трапеция”
Виды трапеций
Элементы трапеции: основания, боковые стороны, средняя линия и высота
Свойства трапеции
Свойства равнобедренной трапеции
Формулы трапеции
Трапеция (понятие, определение):
Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.
Рис. 1. Трапеция
Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
@ https://youtu.be/Q4EpXexoMrM
Виды трапеций:
Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.
Рис. 2. Равнобедренная трапеция
Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.
Прямоугольная трапеция – это трапеция, имеющая прямые углы при боковой стороне.
Рис. 3. Прямоугольная трапеция
Элементы трапеции: основания, боковые стороны, средняя линия и высота:
Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.
Рис. 4. Трапеция
AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.
AD – большее основание трапеции, BC – меньшее основание трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.
Рис. 5. Трапеция и срединная линия
Расстояние между основаниями трапеции называется высотой трапеции.
Рис. 6. Трапеция
Высота трапеции (h) определяется формулой:
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
Свойства трапеции:
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Рис. 7. Трапеция и срединная линия
MN || BC, MN || AD,
l = (a + b) / 2
2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
Рис. 8. Трапеция
MN = (b – a) / 2
3. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360° .
Сумма углов, прилежащих к боковой стороне трапеции, равна 180° .
Рис. 9. Трапеция
4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
Рис. 9. Трапеция
5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

AB = BK
6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Рис. 11. Трапеция
∠BAD + ∠CDA = 90°, MN = (AD – DC) / 2
7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
Рис. 12. Трапеция
AB + CD = AD + BC
В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
Рис. 13. Трапеция
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
Рис. 14. Трапеция
MN = (AB + CD) / 2,
MN = (AD + BC) / 2
8. Диагонали трапеции делят ее на 4 треугольника.
Два из них, прилежащие к основаниям, подобны.
Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.
Рис. 15. Трапеция
Треугольники BCO и AOD подобны. Коэффициент подобия треугольников (k) находится как отношение оснований трапеции. k = AD / BC. Отношение площадей этих подобных треугольников есть k2.
Треугольники ABO и CDO имеют одинаковую площадь.
9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.
Рис. 16. Трапеция
BC : AD = OC : AO = OB : DO
10. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c 2 + d 2
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.
Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия
Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия, UV – отрезок, который соединяет основания трапеции
12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:
где b – большее основание трапеции, a – меньшее основание трапеции, S1 и S2 – площади образованных трапеций, в результате разделения средней линией.
Рис. 18. Трапеция
S1 – площадь трапеции MBCN,
S2 – площадь трапеции AMND
Свойства равнобедренной трапеции:
1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.
2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
3. Углы при любом основании равнобедренной трапеции равны.
4. Сумма противоположных углов равнобедренной трапеции равна 180°.
5. Длины диагоналей равнобедренной трапеции равны.
6. Вокруг равнобедренной трапеции можно описать окружность.
7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.
Формулы трапеции:
Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d1 и d2 – диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.
Формулы для определения сторон трапеции:
Через среднюю линию и одно из оснований трапеции:
a = 2m – b
b = 2m – a
Через высоту и углы при нижнем основании трапеции:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
Через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
Через высоту и углы при нижнем основании трапеции:
Формулы для определения средней линии трапеции:
Через длины оснований трапеции:
Через площадь и высоту трапеции:
Формулы для определения высоты трапеции:
Через сторону и прилегающий угол при нижнем основании трапеции:
h = c·sin α = d·sin β
Через диагонали трапеции и углы между ними:
Через диагонали трапеции, углы между ними и среднюю линию трапеции:
Через площадь и длины оснований трапеции:
Через площадь и длину средней линии трапеции:
Формула для определения периметра трапеции:
P = a + b + c + d
Формулы для определения площади трапеции:
Через основания и высоту трапеции:
Через среднюю линию и высоту трапеции:
S = m · h
Через диагонали трапеции и угол между ними:
Через все стороны трапеции:
С помощью формулы Герона для трапеции:
Как называется объемная трапеция?
Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.
В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.
Квадрат
Овал
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Трапеция
Тупой угол
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/Q4EpXexoMrM
Коэффициент востребованности
6 656
Какими могут быть углы трапеции?
рисунок 1
Как и все другие четырехугольники и многоугольники, которые изучаются в школьном курсе, трапеция — выпуклый четырехугольник. Поэтому сумма углов трапеции равна 360º (речь идет о внутренних углах).
То есть для трапеции ABCD ∠A+∠B+∠C+∠D=360º.
Поскольку основания трапеции лежат на параллельных прямых, сумма углов трапеции, прилежащих к боковой стороне, равна 180 градусам.
Для трапеции ABCD (рисунок 1)
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB),
∠C+∠D=180º (как внутренние односторонние при AD ∥ BC и секущей CD).
Следовательно, если один из углов, прилежащих к одной боковой стороне, острый, то другой — тупой. Если один из этих углов прямой, другой — тоже прямой.
Суммы углов, прилежащих к боковым сторонам трапеции, равны:
∠A+∠B=∠C+∠D
Могут ли углы трапеции, взятые в последовательном порядке, относиться как
1) 7:3:5:2?
Нет, поскольку 7k+3k≠5k+2k и 7K+2k≠3k+5k.
2) 5:4:6:3?
5k+4k=6k+3k, следовательно, углы трапеции могут быть пропорциональны этим числам.
На рисунке 1 углы прилежащие к основанию AD, оба острые, углы, прилежащие к основанию BC, оба тупые. В паре противолежащих углов ∠A и ∠С, ∠B и ∠D один — острый, другой — тупой.
Существует ли трапеция, у которой два противолежащих угла обо тупые или оба острые?
рисунок 2
Да, такая трапеция существует.
Например, трапеция, изображенная на рисунке 2.
Существует ли трапеция, у которой два противоположных угла оба прямые? Противоположные углы равны?
Нет, такой трапеции не существует (противоположные углы равны у параллелограмма).
Содержание:
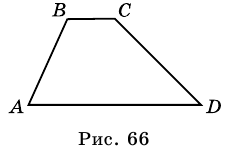
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 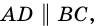
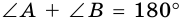
2. Трапеция является выпуклым четырехугольником.
Поскольку 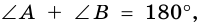
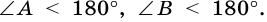
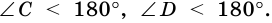
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
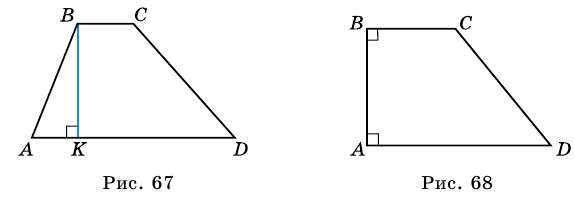
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 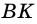
Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 — прямоугольная трапеция 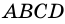
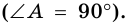
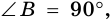
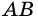
Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 — равнобокая трапеция
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 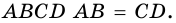
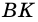
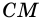
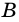
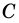
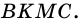
2) 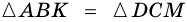
3) Также 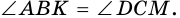
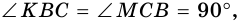
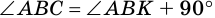
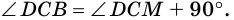
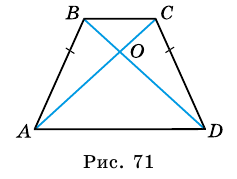
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. 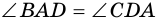
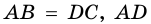
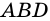
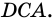
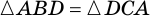
Пример:
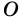
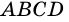
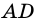
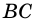
Доказательство:
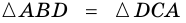
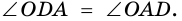
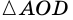
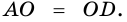
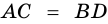
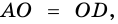
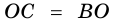
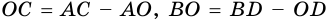
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 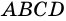
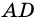
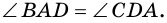
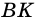
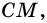
2) Тогда 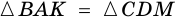
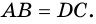
А еще раньше…
Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» — однокоренные).
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие — не параллельны.
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 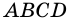
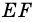
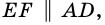
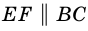
1) Проведем луч 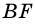
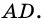
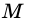
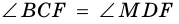
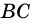
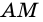
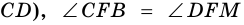
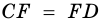
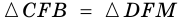
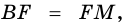
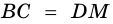
2) Поскольку 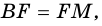
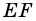
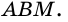
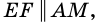
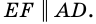
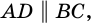
3) Кроме того,
Пример:
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 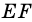
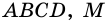
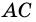
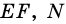
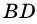
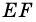
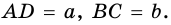
1) Так как 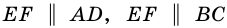
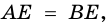
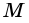
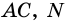
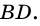
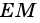
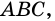
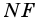
Тогда
2) 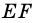
3)
Пример:
В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции — 48 см.
Решение:
Пусть 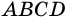
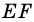
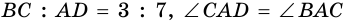
1) Обозначим 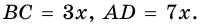
2) 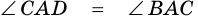
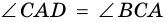
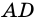
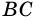
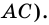
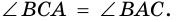
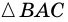
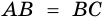
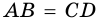
3) Учитывая, что 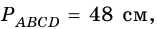
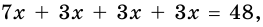
4) Тогда
Ответ. 15 см.
А еще раньше…
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
- Площадь трапеции
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Площадь параллелограмма
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
Трапеция и ее свойства
Т. А. Унегова
Определения:
Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Если боковые стороны равны, трапеция называется равнобедренной.
Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.
Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.
Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.
Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
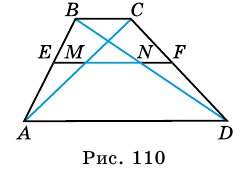
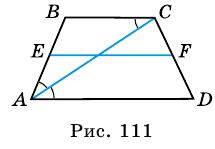
Теоремы о средней линии и диагоналях трапеции
Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: .
Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: .
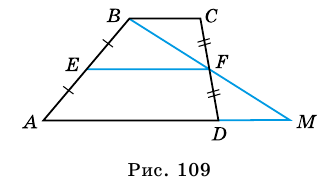
Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: .
Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.
Эта теорема называется также «Замечательное свойство трапеции».
Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.
Теоремы о площади трапеции
Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: .
Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: .
Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: , где
(Вместо
можно брать
Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: . Таким образом,
.
Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)
Теоремы о вписанных и описанных трапециях
Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.
Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.
Задачи ЕГЭ и ОГЭ по теме: Трапеция
Задача 1.
Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны .
Решение:
Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна
, то по теореме Пифагора получаем, что
.
Ответ: 2.
Задача 2.
Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол . Найдите площадь трапеции.
Решение:
Углы ABC и
BAH — односторонние, их сумма равна
, и тогда
BAH
Из ABH найдем высоту BH. Катет, лежащий против угла в
, равен половине гипотенузы. Получаем, что BH = 3,5.
Площадь трапеции равна .
Ответ: 42.
Задача 3.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.
Решение:
Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.
Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что
Ответ: 5.
Задача 4.
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение:
Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что
середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.
Ответ: 0,5.
Задача 5.
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Решение:
Периметр треугольника равен сумме его сторон, то есть
Периметр трапеции равен
Ответ: 23.
Задача 6.
В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол . Найдите углы трапеции.
Решение:
Пусть CAD
, тогда
CAB
и
BAD
, так как трапеция равнобедренная.
Сумма углов , откуда
Итак, , а
.
Ответ: .
Задача 7.
В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.
Решение:
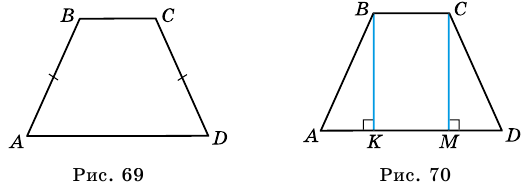
В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и Отсюда,
Ответ: 24.
Задача 8.
Тупой угол равнобедренной трапеции равен , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Решение:
Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом .
Каждый треугольник равнобедренный, поэтому h = 1,4.
Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна .
Ответ: 4,76.
Задача 9.
Площадь трапеции равна 60м а основания 8 м и 12 м. Найдите высоту трапеции.
Решение:
Так как площадь трапеции , то
, откуда h = 6.
Ответ: 6.
Задача 10.
В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.
Решение:
Проведем CE BD и DE — продолжение AD.
Так как BCDE — параллелограмм, то CE = a.
По теореме 10 получим, что .
Ответ:
Задач 11.
В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.
Найдите AD, если периметр трапеции равен 20, а угол D равен .
Решение:
По условию задачи в прямоугольном ACD
D
, следовательно,
CAD
.
Так как AC — биссектриса, то CAB
, откуда
DAB
, то есть, трапеция равнобедренная.
BCA
CAD
как накрест лежащие, поэтому
ABC — равнобедренный.
Обозначим длины боковых сторон ABC буквой x.
Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в
лежит катет, равный половине гипотенузы.
Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда
x = 4 и AD = 8.
Ответ: 8.
Задача 12.
В равнобедренной трапеции ABCD с острым углом меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?
Решение:
Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и
BCM подобен
ADM c коэффициентом
.
Пусть,
, тогда
Площадь трапеции будет равна
Ответ: 35.
Задача 13.
Сумма углов при одном из оснований трапеции равна . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.
Решение:
Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.
Так как сумма углов при основании трапеции равна , то
, поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.
Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит
Ответ: 2.
Задача 14.
Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.
Решение:
Так как площадь трапеции равна , а высота трапеции равна диаметру вписанной окружности, то есть
то
, откуда
.
Ответ: 1,2.
Задача 15.
Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.
Решение:
По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому
откуда
Сторона AB равна диаметру окружности, поэтому .
Ответ: 3.
Задача 16.
Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.
Решение:
Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому
Ответ: 20.
Задача 17.
В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.
Решение:
Так как AD — диаметр окружности, то дуга ABCD равна . Она делится на три равные части по
Вписанный угол D опирается на дугу ABC, которая равна , отсюда
и, стало быть,
Ответ: 120.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023