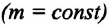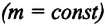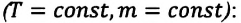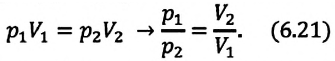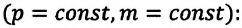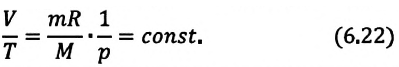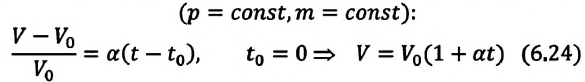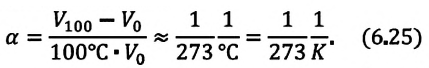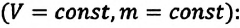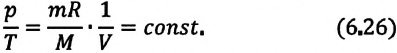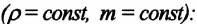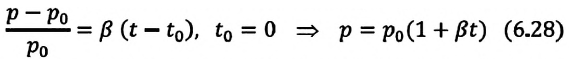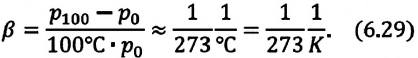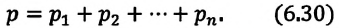Тело плавает в жидкости при условии, что сила Архимеда равна силе тяжести:
FА=Fтяж.
.
Чтобы найти архимедову (выталкивающую) силу, действующую на тело в жидкости, надо плотность жидкости умножить на ускорение свободного падения ((g=9,8) Н/кг) и на объём погружённой в жидкость части тела:
Силу тяжести вычислим по формуле:
Fтяж.=m⋅g=ρтела⋅Vвсего тела⏟∥m⋅g
Подставив соответствующие значения в первую формулу, получим:
ρж⋅g⋅Vчасти тела=ρтела⋅Vвсего тела⋅gρж⋅Vчасти тела=ρтела⋅Vвсего тела⇒Vчасти телаVвсего тела=ρтелаρж
Отношение объёма погружённой части тела к полному объёму тела равно отношению плотности тела к плотности жидкости.
.
На иллюстрации бревно наполовину погружено в воду, потому что его плотность меньше плотности воды в (2) раза.
Айсберг состоит из льда. Его плотность на (10) (%) меньше плотности воды.
Это означает, что часть айсберга, которая находится под водой, в (9) раз больше части айсберга, находящейся над водой. По этой причине айсберги опасны для судов.
Молекулы всех газов при одной и той же
температуре обладают одинаковой средней
кинетической энергией. Причем давление
газа при данной температуре зависит
только от числа молекул в единице объема
газа. В основе объяснений физических
свойств газов и законов газового
состояния лежит кинетическая теория.
Большинство законов газового состояния
было выведено для идеального газа.
Идеальным называют газ, в котором
молекулы рассматриваются как материальные
точки, обладающие массой, но не имеющие
при этом объёма, между которыми отсутствуют
силы взаимодействия.
При
больших объёмах и малых давлениях, когда
расстояние между молекулами во много
раз больше собственных размеров молекул,
а также при высоких температурах, когда
интенсивность хаотического движения
молекул велика и поэтому молекулы слабо
взаимодействуют между собой, складываются
условия, при которых реальный газ можно
с некоторым приближением считать
идеальным.
Закон Бойля — Мариотта.
Английский ученый
Бойль и независимо от него несколько
позднее французский физик Мариотт на
основании экспериментов пришли к выводу
о том, что объем данной
массы газа и его давление находятся в
обратно пропорциональной зависимости.
Эта зависимость между давлением и
объемом газа при постоянной температуре
выражается формулой:
, (1)
где V1
и Р1
– объем и абсолютное давление газа до
их изменения; V2
и Р2 –
то же, после изменения.
Из данной формулы можно получить
следующие математические выражения:
, (2)
или
при
. (3)
Из последней формулы следует,
что произведение
давления данной массы газа на его объем
постоянно, если температура газа не
меняется.
Закон
имеет практическое применение в газовом
хозяйстве. Он позволяет определять
объем газа при изменении его давленная
и давление газа при изменении его объема
при условии, что температура газа
остаётся постоянной.
Чем больше при постоянной
температуре увеличивается объем газа,
тем меньше становится его плотность.
Зависимость между
объёмом газа и его плотностью при
постоянной температуре выражается
формулой
, (4)
где V1
и V2
– объемы, занимаемые газом; ρ1
и ρ2
– плотности газа, соответствующие этим
объемам.
Если в формуле (1) заменим отношение
объемов газа отношением их плотностей,
то на основании формулы (4) можно получить.
или
(5)
Из формулы (5) можно сделать
вывод, что при одной
и той же температуре плотности газов
прямо пропорциональны давлениям, под
которым находятся эти газы, т.е. плотность
газа (при постоянной температуре) будет
тем больше, чем больше будет его давление.
Пример.
Объем газа при давлении 760 мм.рт.ст. и
при температуре 0°С составляет 300 м3.
Какой объем займет этот газ при абсолютном
давлении, равном 1520 мм.рт.ст. и при той
же температуре?
760 мм.рт.ст. = 101 320 Па = 101,3 кПа;
1520 мм.рт.ст. = 202 630 Па = 202,6 кПа.
Подставляем заданные
значения V1,
Р1,
и Р2
в формулу (2):
Р1 =
101,3 кПа; V1
= 300 м3;
Р2 =
202,6 кПа;
101,3 х 300 = 202,6 V2,
откуда V2
= (101,3
х 300)/202,6 = 150 м3.
Закон Гей-Люссака.
Французский химик Гей-Люссак впервые
установил зависимость объема газа от
температуры при постоянном давлении.
Сущность этой зависимости заключается
в том, что при постоянном
давлении относительное изменение объема
данной массы газа прямо пропорционально
изменению температуры.
Математически эта зависимость между
объемом и температурой газа при постоянном
давлении записывается следующим образом:
, (6)
где V
– объем газа, м3;
Т – абсолютная
температура, К.
Из формулы (6) следует, что
если определенный
объем газа нагревать при постоянном
давлении, то его объем изменится во
столько раз, во сколько раз изменится
его абсолютная температура.
Многочисленные опыты
показывают, что при нагревании газов
на 1 градус при постоянном давлении их
объем увеличивается на постоянную
величину, равную 1/273,2 первоначального
их объема. Эта величина называется
термическим
коэффициентом объемного расширения
и обозначается α
= 1/273,2 град-1.
С учетом этого закон
Гей-Люссака можно сформулировать так:
объем данной массы
газа при постоянном давлении увеличивается
линейно при повышении температуры
; (7)
; (8)
, (9)
где Vt
и V0
– объемы газа при
конечной и начальной температурах, м3;
t
и Т – начальная и конечная температуры,
оС,
К; α – термический коэффициент объёмного
расширения.
Из формулы (9) следует, что
объем газа при постоянном
давлении прямо пропорционален его
абсолютной температуре.
Закон Шарля.
Согласно закону Шарля,
давление данной массы
газа при постоянном объеме прямо
пропорционально абсолютной температуре.
Из этого закона следует, что отношение
давлений массы газа при постоянном
объеме равно отношению его абсолютных
температур. Закон
выражается следующей формулой:
или
, (10)
где Р1
и Р2
– абсолютные давления; Т1
и
Т2
– абсолютные температуры
газа, К.
Из формулы (10) можно сделать вывод, что
при постоянном объеме давление газа
при нагревании увеличивается во столько
раз, во сколько раз увеличивается его
абсолютная температура.
Пример 1.
При температуре газа 27°С его давление
равно 4 МПа (40 кгс/см2).
Каково будет избыточное давление этого
газа при температуре 47°С?
Начальная абсолютная
температура газа равна:
,
конечная абсолютная
температура газа равна:
.
Атмосферное давление примем
равным 0,1 МПа (1 кгс/см2),
тогда абсолютное давление газа до
нагревания будет:
.
Искомое абсолютное давление
газа Р2
по формуле (10) равное:
.
Следовательно, избыточное давление
газа после нагревания его до 47°С равно:
.
Пример 2.
Сжатый газ в баллоне при температуре
7°С имел избыточное давление 0,9МПа. После
нагревания давление в баллоне повысилось
до 1,1 МПа. До какой температуры был нагрет
газ?
Начальная абсолютная
температура газа:
.
Начальное абсолютное
давление газа:
.
Конечное абсолютное давление
газа:
.
Из формулы (10) после
преобразования ее относительно
неизвестной Т2
получаем:
.
Следовательно, газ в баллоне был нагрет
до температуры 63°С.
Закон
Авогадро. Итальянский
ученый Амадео Авогадро выразил
предположение, что различные
газы, занимающие одинаковые объёмы при
равных условиях (одинаковые давление
и температура), содержат одинаковое
число молекул.
Это число для одной
грамм-молекулы (1 моль) любого газа
составляет около N
= 6,064 х
1023
и называется числом Авогадро. В дальнейшем
было экспериментально установлено, что
1 грамм-молекула любого газа при нормальных
условиях занимает объем 22,4л.
В Международной системе
единиц производной является величина,
в 1000 раз большая моля, она называется
киломоль и
обозначается кмоль.
1 кмоль любого газа
при нормальных условиях (0°С и 101,3 кПа)
занимает объем 22,4 м3.
Зная эту величину, можно определить
плотность любого газа по формуле
, (11)
где М —
масса 1 кмоля газа, кг.
Пример 1.
Определить плотность метана при
нормальных условиях (ОоС
и 101,3 кПа):
.
Пример 2. В баллоне находится 100 кг
жидкого этана. Определить объем паров
этана, полученных при его полном испарении
в нормальных условиях.
Решение. Сначала определяют число
киломолей этана:
п = 100 : 30,07 = 3,33 (здесь 30,07 –
молекулярная масса этана).
Зная, что 1 киломоль этана при испарении,
т.е. в газообразном состоянии, занимает
объем 22,4 м3, находят объем паров
этана от испарения всего его количества:
V = 22,4 х
3,33 = 74,63 м3.
Уравнение Клапейрона —
Менделеева.
При одновременном изменении объема,
давления и температуры газа справедливы
законы и Бойля — Мариотта и Гей-Люссака.
Французский ученый Клапейрон пришел к
выводу о существовании для газов
некоторой универсальной функции. Русский
ученый Д.И. Менделеев вывел в более общем
виде уравнение состояния идеальных
газов, объединив уравнения законов
Бойля — Мариотта и Гей-Люссака в одно
общее математическое уравнение идеального
газа, которое называется уравнением
Клайперона—Менделеева:
. (12)
Величина
обозначается буквой “R”
называется газовой постоянной. Подставляя
обозначение газовой постоянной в формулу
(12), получаем выражение:
или
. (13)
Это
уравнение закона газового состояния
связывает все три основных параметра
данного количества газа: объем, абсолютное
давление и абсолютную температуру, и
оно относится к 1 молю газа.
Из уравнения следует, что
для определенного
количества газа произведение его объема
на абсолютное давление равно произведению
газовой постоянной на абсолютную
температуру газа. Числовое
значение газовой постоянной зависит
от величин параметров, входящих в
уравнение (13).
В Международной системе универсальная
газовая постоянная для 1 кмоля равна:
,
где 101325 – нормальное давление, Па.
Уравнением Клапейрона —
Менделеева часто пользуются при пересчете
характеристик газа. Формулы (14) и (15),
предназначенные для пересчета параметров,
характеризующих состояние газа в
нормальных и стандартных условиях,
получены путем соответствующих,
преобразований выражения
.
, (14)
, (15)
где VН Vст
– объём газа при нормальных и стандартных
условиях, м3; Vt
– объём газа при реальных условиях, м3;
Pt –
давление газа при реальных условиях,
Па; Р – давление газа при нормальных и
стандартных условиях (101325 Па).
Закон Дальтона.
Смеси газов (паров),
близких по своим свойствам к идеальным,
характеризуются аддитивностью парциальных
давлений. Аддитивность
(от лат. additivus
– прибавляемый), свойство объекта, по
которому величина всего объекта равна
сумме величин частей объекта при любом
разбиении. Так, масса тела равна сумме
масс его частей.
Парциальным давлением
компонента ρi
газовой смеси называется то давление,
которое этот компонент оказывал бы,
если бы из смеси удалить все другие
компоненты при сохранении первоначальных
объема и температуры системы. Закон
аддитивности записывается следующим
образом:
(16)
где π — общее давление смеси
газов (паров). Из уравнения
следует, что
(17)
Подставив это выражение в уравнение
(17), получим
(18)
Следовательно
(19)
или
(20)
т.е. парциальное
давление компонента равно давлению
системы, умноженному на мольную долю
этого компонента в газовой фазе.
Пример. Известен молярный состав
смеси газов, %: метан – 90, этан – 5, пропан
– 2, азот – 2, бутаны – 1. Смесь находится
под давлением 12 МПа. Требуется определить
парциальное давление компонентов смеси.
Решение. Пользуясь уравнением, вычисляют
парциальное давление компонентов:
pC1
= 0,9*12 = 10,8 МПа;
pC2
= 0,05*12 = 0,6 МПа;
pC3
= 0,02*12 = 0,24 МПа;
pC4
= 0,02*12 = 0,24 МПа;
pC5
= 0,01*12 = 0,12 МПа.
Законы реальных газов.
При повышении давления
объем реального газа становится меньше,
чем идеального. Это
обстоятельство учитывают введением
соответствующих поправок в законы
идеальных газов.
Так,
уравнение состояния реального газа
можно записать в виде:
(21)
где z
— коэффициент сжимаемости, являющийся
функцией приведенного давления Рпр
= P/Pкр
и приведенной
температуры Tпр
= T/Ткр;
Ркр
и Ткр
— критические давление и температура
(табличные значения).
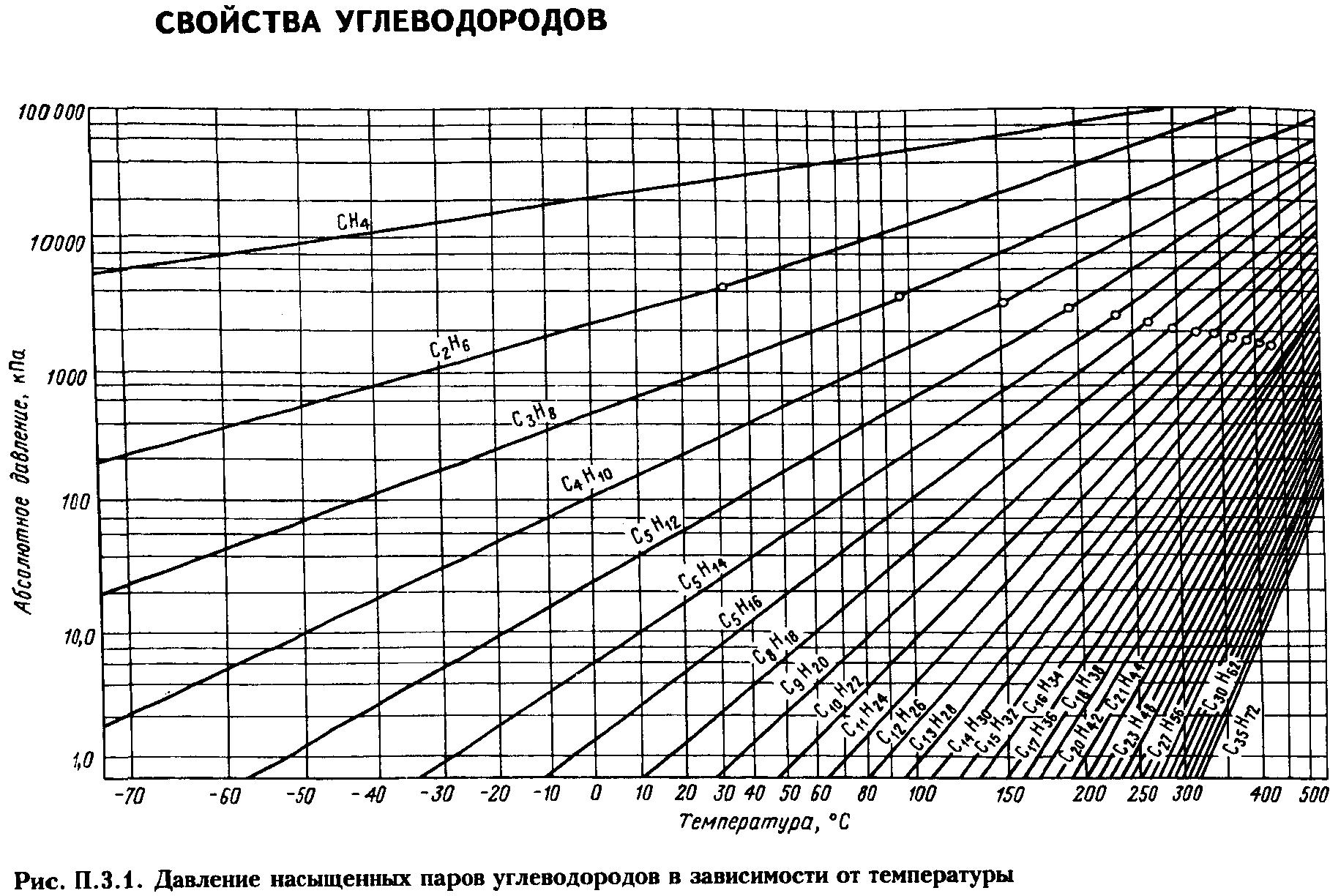
Давление насыщенных
паров. Пары жидкости
могут быть насыщенными и ненасыщенными.
Насыщенным называется
пар, находящийся в равновесии с жидкостью.
Чем выше температура, тем выше давление,
при котором находится данная равновесная
система. Для насыщенных паров существует
однозначная зависимость между давлением
паров и температурой Р
= f(T).
Ненасыщенными (перегретыми)
парами называют пары, которые при данных
температуре и давлении образуют
однофазную систему.
Жидкая фаза отсутствует.
Известно, что жидкость
начинает кипеть при такой температуре,
при которой давление её насыщенных
паров Р
становится равным внешнему давлению
π. Давление насыщенных паров определяют
по табличным данным или эмпирическим
уравнениям (ур-е Антуана, Киреева).
Для определения ДНП
нефтепродуктов, представляющих собой
сложные смеси углеводородов различных
классов, предложены графики и формулы
(Кокса, Ашворта, Вильсона, BWR
и др.)
Закон Рауля. Этот закон
устанавливает зависимость между
парциальным давлением компонента,
входящего в состав раствора, его молярной
концентрацией в жидкой смеси Х
и упругостью пара того же чистого
компонента при заданной температуре
Q.
Парциальное давление компонента в
жидкой смеси равно его молярной
концентрации, умноженной на упругость
его паров в чистом виде при данной
температуре:
(22)
где р – парциальное давление
компонента в растворе.
По закону Рауля, сумма парциальных
давлений всех компонентов равна общему
давлению над смесью или общей упругости
паров смеси:
где
ХnQn
– молярная концентрация и упругость
паров компонента соответственно.
Пример. Жидкая смесь состоит из
этана –60%, пропана –25 % и изобутана
–15 % (молярные доли). Требуется определить
общее давление системы при температуре
100С.
Решение. Сначала из рис. 2.1 (график Кокса)
находим давление насыщенных паров
компонентов в чистом виде при 10°С:
QC2
= 0,326 МПа; QC3
= 0,63 МПа; QC4
= 0,16 МПа
Затем по уравнению определим общее
давление системы:
Данные этого примера показывают, что
если бы указанная смесь транспортировалась
в жидком виде при 10°С, то трубопровод
работал под давлением 2,14 МПа.
Важным выводом, вытекающим из закона
Рауля, является то, что высококипящие
компоненты имеют низкую упругость,
содержатся в паровой фазе в малых
количествах; следовательно, их
основная доля находится в жидкой фазе.
Что касается низкокипящих компонентов,
обладающих высокой упругостью, то они
легко переходят в газовую фазу. На этом
положении основана работа многих
установок по частичной стабилизации
газового конденсата при выветривании
– ступенчатом снижении давления смеси
с одновременным ее расширением.

23
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основы термодинамики. Тепловое равновесие. Уравнение Клапейрона-Менделеева. Изопроцессы.
В. З. Шапиро
Восьмое задание ЕГЭ по физике проверяет знания по разделам «Молекулярная физика» и «Термодинамика». Оно относится к заданиям базового уровня. В нём нет возможности выбора ответа. Данные для условия задачи могут быть представлены в виде текста или на графике.
Необходимая теория: Основные положения молекулярно-кинетической теории
1. В сосуде находится некоторое количество идеального газа. Во сколько раз уменьшится объём газа, если он перейдёт из состояния 1 в состояние 2 (см. рисунок)?
Ответ: в ___________________________ раз(а).
Для точек 1 и 2 надо применить уравнение Клапейрона, так как масса газа и количество вещества остается неизменным.
отсюда можно выразить отношение объемов в состояниях 1 и 2.
Подставим условные значения для температуры и давления из графика
Ответ: в 2 раза.
Секрет решения: Уравнение Клапейрона применимо только для неизменной массы или количества вещества идеального газа. Более универсальным является уравнение Менделеева-Клапейрона. Его можно использовать для различных масс и количеств вещества газа. От этого уравнения легко перейти к уравнению Клапейрона, сократив на равные массы.
2. Цилиндрический сосуд разделён лёгким подвижным поршнем на две части. В одной части сосуда находится криптон, в другой – аргон. Температуры газов одинаковы. Определите отношение концентрации молекул криптона к концентрации молекул аргона.
Ответ: ___________________________.
Наличие легкого подвижного поршня в цилиндрическом сосуде приведет к выравниванию давлений в обеих частях. Для решения задачи необходимо использовать формулу для связи давления, концентрации и температуры.
– для сосуда с криптоном,
– для сосуда с аргоном. Приравнивая эти два уравнения (так как давления одинаковые) получим:
Ответ: 1.
3. Температура неона увеличилась с 27 оС до 327 оС. Во сколько раз увеличилась средняя кинетическая энергия его молекул?
Ответ: в___________________________ раз(а).
Температура связана со средней кинетической энергией молекул формулой:
применим эту формулу для двух случаев, переведя температуру из градусов Цельсия в градусы Кельвина.
Найдем отношение
Подставим численные значения
Ответ: 2.
Секрет решения: Перевод температуры в шкалу Кельвина является обязательным во всех разделах физики. Связь запоминается легко, но также надо знать, что при изменении температуры на один градус по Цельсию температура по Кельвину также меняется на один градус.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 8 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
2018-03-10
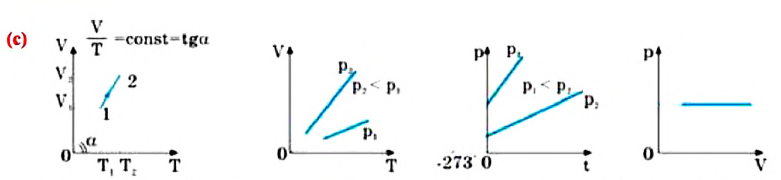
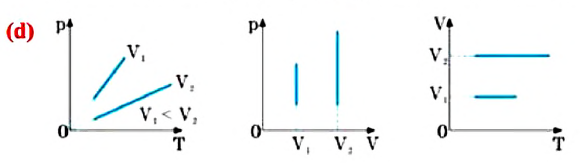
Над идеальным газом совершают цикл 1—2—3, изображенный на диаграмме р—Т (рис.). Найти отношение максимального и минимального объемов.
Решение:
На диаграмме р—Т изохоры представляют собой прямые, проходящие через начало координат, причем тангенс угла наклона изохоры обратно пропорционален объему газа. Мысленно проведя нзохоры, нетрудно убедиться, что максимальный $V_{max}$ объем газа будет в точке 2, а минимальный $V_{min}$ — в точке 1. Воспользовавшись законом Менделеева—Клапейрона, запишем
$frac{ 2p_{1}V_{min} }{T_{1} } = frac{p_{1}V_{max} }{3T_{1} }$,
Отсюда сразу находим искомое отношение объемов $V_{max}/V_{min} = 6$.
Преподаватель который помогает студентам и школьникам в учёбе.
Газовые законы в физике — формулы и определения с примерами
Содержание:
Газовые законы:
С помощью уравнения состояния идеального газа можно исследовать процессы, при которых сохраняются постоянными масса газа и один из его макроскопических параметров.
Газовыми законами называются законы, определяющие количественную зависимость между двумя макроскопическими параметрами газа данной массы
Изопроцессами (греч.: izos — «равный «) называются процессы, протекающие в газах данной массы
Закон Бойля-Мариотта
Этот закон был определен в 1662 году английским физиком Робертом Бойлем (1627-1691) и в 1676 году французским физиком Эдом Мариоттом (1620-1684).
Для данной массы газа при неизменной температуре произведение давления газа на его объем постоянно
Для данной массы газа при неизменной температуре произведение давления начального состояния 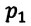
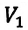
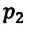
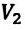
Изотермическим называется процесс изменения состояния данной массы идеального газа при постоянной температуре 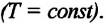
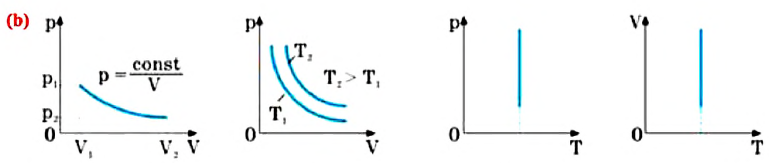
Закон Гей-Люссака
Этот закон был экспериментально установлен в 1802 году французским физиком Джозефом Луи Гей-Люссаком (1778-1850).
Для данной массы газа при неизменном давлении отношение объема газа к его абсолютной температуре постоянно
При неизменном давлении отношение первоначального объема газа 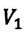
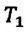
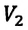
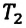
Закон Гей-Люссака можно выразить и так:
Для данной массы идеального газа при неизменном давлении относительное
Где 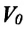
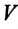
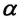
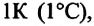
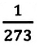
Изобарным называют процесс изменения состояния данной массы идеального газа при постоянном давлении 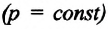
- Заказать решение задач по физике
Закон Шарля
Этот закон экспериментально определил в 1787 году французский физик Шарль Жак Александр Сезар (1746-1823):
Для данной массы газа при постоянном объеме отношение давления газа к его абсолютной температуре остается неизменным
Отношение первоначального давления 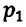
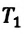
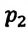
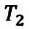
Закон Шарля можно выразить и так:
Для данной массы идеального газа при неизменном объеме относительное изменение давления прямо пропорционально изменению температуры
Где 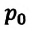
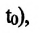
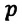
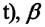
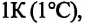
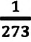
Изохорным называется процесс изменения состояния данной массы идеального газа при постоянном объеме 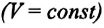
Закон Дальтона
Этот закон в 1801 году установил английский исследователь Джон Дальтон (1766-1844):
Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений этих газов:
Парциальное давление — это давление отдельно взятого газа из газовой смеси.
Закон Авогадро
Этот закон, как предположение, был выдвинут в 1811 году итальянским физиком Амедео Авогадро (1776-1856). В последующем это предположение было подтверждено многочислеными опытами.
В равных объемах различных газов, взятых при одинаковых температурах и давлении, содержится одинаковое число молекул. Например, число молекул в 1 моле произвольного газа равно: 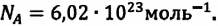
- Взаимодействие молекул
- Агрегатное состояние вещества
- Зависимость размеров тел от температуры
- Световые явления
- Физическое тело и вещество в физике
- Плотность и единицы плотности в физике
- Движение молекул в физике в газах, жидкостях и твёрдых телах
- Скорость движения молекул газа