Как найти острые углы египетского треугольника

Египетский треугольник — загадка древности

Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.

История открытия

Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а

Применение

Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.

Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других – 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.

Доказательство

При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.

Что такое Египетский треугольник на стройке? В чем его особенность +Фото и Видео

Строительство с применением египетского треугольника древний способ, активно используемый до сих пор современными строителями. Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.

Но, скорее всего, свойства уникальной фигуры не были оценены в те времена, пока не появился Пифагор, сумевший проанализировать и оценить изящные формы фигуры.

Египетский треугольник известен еще с древних времен. Он был и остается популярен в строительстве и архитектуре много веков.

Считается, что создал геометрическую конструкцию великий греческий математик Пифагор Самосский. Благодаря ему сегодня мы можем использовать все свойства геометрической постройки в области строения.

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51 о 50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

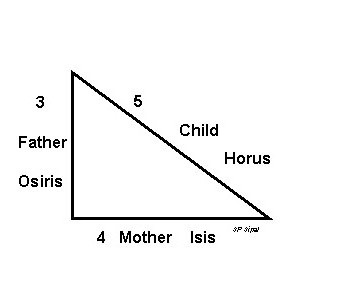
Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53 о 12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 3 2 х4 2 =5 2 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Место в строительном мире

С древнейших времен египетский треугольник нашел почетное место в архитектуре и строительстве. Конструкция пирамиды отличается тем, что позволяет создавать здание с совершенно правильными углами без каких-либо дополнительных инструментов.

Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.

Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.

Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.

Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.

Какие существуют альтернативные варианты

Как создать прямой угол

Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.

В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.

Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.

Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.

Как создать другие углы?

Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.

Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол. Края должны быть соединены.

Получить 60 градусов можно с применением двух треугольников по 30 градусов. Чаще всего используются для создания декоративных элементов.

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

Египетский треугольник

В математике есть определенные каноны, которые явились, так сказать, фундаментом или основанием всего последующего развития современной математики. Одним из этих канонов, по праву можно считать теорему Пифагора.

Кому еще со школьных времен не известна смешная формулировка теоремы Пифагора: «Пифагоровы штаны во все стороны равны». Ну да, правильно это звучит так: «квадрат гипотенузы равен сумме квадратов катетов «, но про штаны гораздо лучше запоминается.

Нагляднее всего это видно на треугольнике со сторонами 3-4-5. Но если изучить внимательно использование такого треугольника в древней истории, то можно заметить одну занимательную вещь и называется она ни как по другому, как Египетский треугольник.

Этот самый философ и математик Пифагор Самосский из Греции, именем которого и названа эта теорема, жил примерно 2,5 тысяч лет тому назад. Ну конечно дошедшая до нашего времени биография Пифагора не совсем достоверна, но, тем не менее, известно что Пифагор много путешествовал по странам Востока. В том числе он был и Египте и Вавилоне. В Южной Италии Пифагор основал свою знаменитую «Пифагорову школу», которая сыграла очень даже важную роль, как в научной, так и политической жизни древней Греции. С тех времен по преданиям Плутарха, Прокла и других известных математиков того времени, считалось, что эта теорема до Пифагора известна не была и именно по этому её назвали его именем.

Но история говорит что это не так. Обратимся туда, где бывал Пифагор и что видел, прежде чем сформулировать свою теорему. Африка, Египет. Бесконечный и однообразный океан песка, почти ни какой растительности. Редкие кустики растений, едва заметные верблюжьи следы. Раскаленная пустыня. Солнце и то кажется тусклым, как будто покрытым этим вездесущим мелким песком.

И вдруг, как мираж, как видение, на горизонте возникают строгие очертания пирамид, изумительных по своим идеальным геометрическим формам, устремленным к палящему солнцу. Своими огромными размерами, и совершенством своих форм они изумляют.

Скорее всего, Пифагор их видел в ином виде, нежели как они выглядят сейчас. Это были сияющие полированные громады с четкими гранями на фоне многоколонных прилегающих храмов. Рядом с величественными царскими пирамидами стояли пирамиды поменьше: жен и родичей фараонов.

Власть фараонов Древнего Египта была непререкаемой. Фараонов считали божеством и отдавали им божественные почести. Фараон-бог был вершителем судьбы народа и его покровителем. Даже после смерти культ фараона имел преогромное значение. Умершего фараона сохраняли веками, и для сохранения тела фараона сооружали гигантские пирамиды. Величие, архитектура и размеры этих пирамид поражают и сейчас. Недаром эти сооружения относили к одному из семи чудес света.

Изначально назначение пирамид было не только как усыпальниц фараонов. Считают что они сооружались как атрибуты могущества, величия, и богатства Египта. Это памятники культуры того времени, хранилища истории страны и сведений о жизни фараона и его народа, собрание предметов быта того времени. Кроме того однозначно, что пирамиды имели определенное «научное содержание». Их ориентирование на местности, их форма, размеры и каждая деталь, каждый элемент настолько тщательно продумывались, что должны были продемонстрировать высокий уровень знаний создателей пирамид. Очевидно что они строились на тысячелетия, «навечно». И недаром арабская пословица гласит: «Все на свете страшится времени, а время страшится пирамид».

Своим аналитическим умом Пифагор не мог не заметить определенную закономерность в формах и геометрических размерах пирамид. Скорее всего, это и натолкнуло Пифагора на анализ этих размеров, что впоследствии и было им выражено своей знаменитой теоремой, от которой ныне и отталкивается современная геометия.

Среди множества пирамид сохранившихся до нашего времени особое место занимает пирамида Хеопса. Если рассмотреть геометрическую модель этой пирамиды и восстановить её первоначальную форму, то очевидно, что её поперечное сечение представляет собой два треугольника с внутренним углом равным 51°50′.

Сейчас пирамида является усеченной, но это разрушения времени, а если геометрически восстановить её в первоначальном виде, то получается что стороны этих треугольников равны: основание СВ = 116, 58 м, высота АС = 148,28 м.

Отношение катетов у/х = 148,28/116,58 = 1,272. А это величина тангеса угла 51град 50 мин. Получается, что в основу треугольника АСВ пирамиды Хеопса было заложено отношение AC/CB = 1,272. Такой прямоугольный треугольник называется «золотым» прямоугольным треугольником.

Получается что основной «геометрической идеей» пирамиды Хеопса является «золотой» прямоугольный треугольник. Но особой в этом отношении является пирамида Хефрена. Угол наклона боковых граней у этой пирамиды равен 53°12, при котором отношение катетов прямоугольного треугольника 4:3. Такой треугольник называют «священным» или «египетским» треугольником. По мнению многих известных историков, «египетскому» треугольнику в древности придавали особый магический смысл. Так Плутарх писал, что египтяне сопоставляли природу Вселенной со «священным» треугольником: символически они уподобляли вертикальный катет мужу, основание — жене, а гипотенузу — тому, что рождается от обоих.

Для египетского треугольника со сторонами 3:4:5 справедливо равенство: 32 + 42 = 52, а это и есть знаменитая теорема Пифагора. По неволе напрашивается вопрос: не это ли соотношение хотели увековечить египетские жрецы, построив пирамиду в основе которой лежит треугольник 3:4:5. Пирамида Хефрена наглядное подтверждение того что знаменитая теорема была известна египтянам задолго до ее открытия Пифагором.

Неизвестно как это попало к древним египтянам, то ли это заслуга их ученых, то ли это дар из вне, не исключается и то, что это дар внеземной цивилизации, но использование такого треугольника давало египетским строителям очень существенную и к тому же простую возможность при возведении таких огромных сооружений соблюдать точные геометрические размеры. Ведь свойства этого треугольника таковы, что его угол между катетами является равный 90 градусов. То есть использование такого элемента позволяет обеспечить точную перпендикулярность сопрягаемых элементов и естественно всей конструкции, что и подтверждает архитектура древнего Египта.

Получить прямой угол без необходимых инструментов не просто. Но если воспользоваться этим треугольником, оказывается все достаточно просто. Нужно взять обычную веревку, разделить её на 12 равных частей, и из них сложить треугольник, стороны которого будут равны 3, 4 и 5 частям. Угол между сторонами длиной 3 и 4 части оказывается и есть прямой. Вот это и есть Египетский треугольник Пифагора.

Во многих исторических письменах имеются следы, что уникальные свойства «египетского треугольника» были известны и широко использовались за много веков до Пифагора и не только в Египте, но и далеко за его пределами: в Месопотамии, в древнем Китае, в Вавилоне.

Знаменитая древнеегипетская пословица «Делай, как делается», дошедшая до наших дней, наталкивает на мысль что сами египтяне, возводившие эти строительные шедевры, были простыми исполнителями и особыми знаниями не обладали, а все секреты были скрыты от непосвященных. Ведь работами на строительстве руководили жрецы — члены особой привилегированной замкнутой касты. Они были хранителями древних знаний, которые держались в секрете. Но пытливый ум великого мыслителя Пифагора сумел разгадать один их этих секретов.

Умы людей всегда будоражат разнообразные загадки, и это, вероятно, будет всегда. Египетский треугольник, хоть и известен человечеству с незапамятных времён, все-таки одна из не полностью разгаданных тайн.

Ведь, что не говори, а форма египетского треугольника и проста, и в то же время гармонична, по своему он даже красив. И с ним достаточно легко работать. Для этого можно использовать самые простые инструменты — линейку и циркуль. Использую этот незатейливый элемент и его симметричные отображения, можно получить красивые, гармоничные фигуры. Это и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих — возрастающих, по размерам египетских треугольников в соответствии с правилом золотого сечения. Это удивительное богатство гармоничных пропорций.

До сих пор в мире есть много пытливые люди, которые как безумцы изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Скорее всего, усилия их тщетны, но даже в случае с Египетским треугольником, ясно что «простых тайн» на земле еще много.

Точный угол 90 градусов с помощью рулетки

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

Источник

Египетский треугольник. Прямой угол без инструмента.

15.01.2016 profipol_dp 3 710 просмотра

Как выставить угол 90 градусов без специального инструмента (угольника)?

Допустим, у нас есть линия к которой нам нужно выставить перпендикуляр, т.е. еще одну линию под углом 90 градусов относительно первой. Или у нас есть угол (например, угол комнаты) и нам нужно проверить равен ли он 90 градусам.

Есть две отличные штуки, такие как «Египетский треугольник» и теорема Пифагора, которые нам в этом помогут.

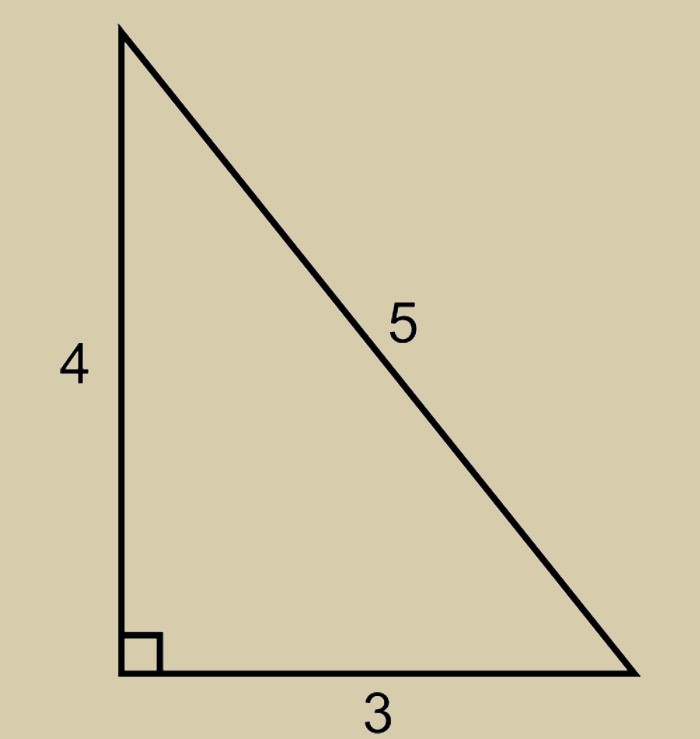
Итак, Египетский треугольник — это прямоугольный треугольник с соотношением всех сторон равным 3:4:5 (катет 3: катет 4: гипотенуза 5).

Египетский треугольник напрямую связан с теоремой Пифагора — сумма квадратов катетов равна квадрату гипотенузы (3*3 + 4*4 = 5*5).

Как нам это может помочь? Все очень просто.

Задача №1. Н ужно построить перпендикуляр к прямой линии (например, линию под 90 градусов к стене).

Шаг 1. Для этого от точки №1 (где будет наш угол) нужно отмерить на этой линии любое расстояние кратное трем или четырем — это будет наш первый катет (равный трем или четырем частям, соответственно), получаем точку №2.

Для простоты вычислений можно взять расстояние, например 2м (это 4 части по 50см).

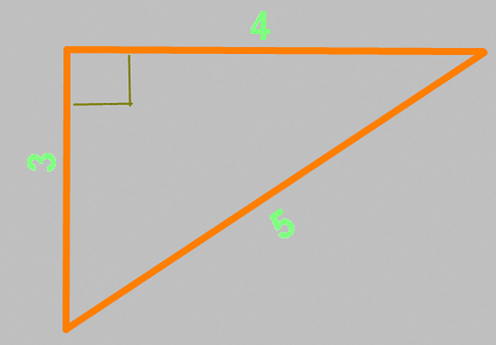
Шаг 2. Затем от этой же точки №1 отмеряем 1,5м (3 части по 50см) вверх (выставляем примерный перпендикуляр), чертим линию (зеленая).

Шаг 3. Теперь из точки №2 нужно поставить метку на зеленой линии на расстоянии 2,5м (5 частей по 50см). Пересечение этих меток и будет нашей точкой №3.

Соединив точки №1 и №3 мы получим линию-перпендикуляр нашей первой линии.

Задача №2. Вторая ситуация — есть угол и нужно проверить прямой ли он.

Вот он, наш угол. Крнечно проще проверить большим угольником. А если его нет?

Отмеряем от угла любую длину кратную четырем, в данном случае это 1,6м.

В другую сторону три части, соответственно 1,2м.

И между этими точками должно оказаться пять частей, т.е. 2м.

Как видите, у нас угол оказался прямее всех прямых.

Источник

Три варианта построения прямого угла на местности. Как проверить угол уже построенного дома, когда замер диагоналей невозможен?

В данной статье описываются три распространенных варианта построения прямых углов при разметке участка для будущего дома, а также описываются методы проверки углов уже возведенных зданий и сооружений без доступа к замеру их диагоналей.

На самом же деле, вариантов существует множество и большинство из них выражаются через тригонометрические функции или с помощью сложных геометрических построений, но здесь это ни к чему, на стройплощадке ни один строитель не возьмется за сложные вещи, упуская время.

Поэтому, рассмотрим три самых простых, но тем не менее надежных метода построения прямых углов:

Теорема Пифагора

Это самый часто используемый и очень надежный способ.

Теорема Пифагора устанавливает соотношение между сторонами прямоугольного треугольника и звучит так: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Для построения прямого угла можно воспользоваться готовым решением (рисунок ниже) или же зная стороны дома, можно без труда вычислить значение диагонали для своего дома и в дальнейшем работать с полученным значением.

Основное соотношение сторон треугольника Пифагора — 3, 4 и 5 единиц. Для удобства, существуют производные треугольники от основного, получаемые при умножении сторон треугольника Пифагора на какой-либо коэффициент. К примеру, стороны 3,4,5 умноженные на К=2 (коэффициент 2), дают треугольник со сторонами 6,8,10, при К=3, стороны 9,12,15 и т.д.

Геометрическое построение

Данный способ ни чуть не хуже Пифагорова треугольника, но редко используемый (в силу забывчивости школьных знаний), хотя очень даже эффективный!

Выглядит сложнее, чем на самом деле.

Зная угол здания (точка О), отмечаем две точки О1 и О2 по оси А, равноудаленные от точки О. Одинаковое расстояние откладывается с помощью рулетки.

Точки О1 и О2 являются центрами окружностей одинакового радиуса. Прямая, проведенная через точку пересечения двух окружностей (точка В) и точку О будет давать прямой угол с прямой А.

По факту, этот способ ни чуть не хуже треугольника Пифагора, имея под рукой два колышка и отрезок веревки, построение осей будущего дома производится всего за 20-40 минут в зависимости от размера и сложности здания.

Две рулетки

Вместо построения окружностей из точек О1 и О2, используются две рулетки (рулетки без погрешности между собой, допустимое отклонение 2-3 мм. на 10 м. по размерной шкале) и прикладываются нулевой отметкой к каждой из точек О1 и О2.

Далее, совмещаем их одинаковыми значениями по мерным шкалам (точка Х) и получаем точку Х, соединив которую с точкой О получим перпендикуляр. В данном случае, построен равнобедренный треугольник, где его высота делит основание ровно пополам и образует с ним прямой угол.

На практике это делается следующим образом: отмечается три контрольные точки по двум рулеткам на пересечении делений (к примеру 1 м., 3м. и 7м.). Далее, через них протягивается разметочный шнур из точки О. Если все точки пересечения шкал лежат на одной прямой (совпадают со шнуром), то построение выполнено верно.

Это настолько быстро делается, что на первый взгляд может показаться неправдоподобным, но поверьте — геометрия работает со 100% гарантией.

Проверка прямого угла построенного здания

Все вышеописанные способы так же применимы и к уже стоящим зданиям. Они используются как проверка за строителями, а так же в случаях, если требуется сооружать фундамент по периметру старого дома и/или ровно облицевать ветхий домик каким-либо материалом.

Все действия аналогичны и главное правило заключается в том, чтобы вынести замеры за пределы строения.

Используя бечевку, протягиваем ее параллельно стенам и закрепляем колышками, а после — снимаем замер.

При геометрическом построении, точка пересечения двух окружностей будет лежать не в основании стены, а по «невидимому» продолжению стены в её же плоскости (на рисунке обозначена точкой Х).

При необходимости, все способы свободно комбинируются или взаимозаменяются.

На этом всё, спасибо Вам за уделенное внимание!

Источник

Как создать или проверить прямой угол при помощи рулетки

При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.

Теорема Пифагора

Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: »В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов» ( a 2 + b 2 = с 2 ), где a и b — катеты, а с — гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.

А теперь вернемся к нашим замерам и применим теорему на практике.

Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.

Египетский треугольник

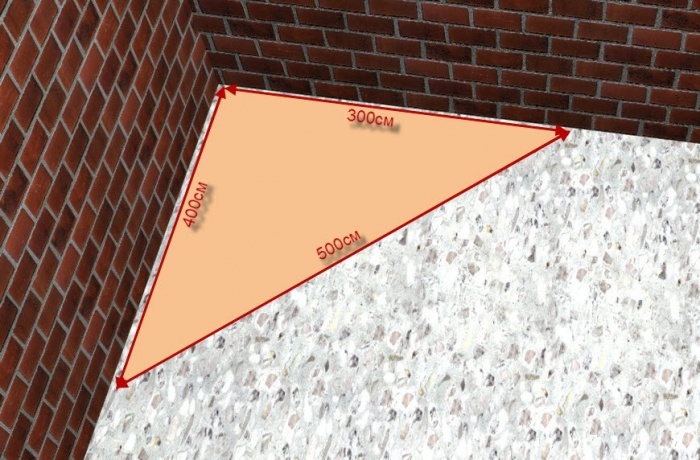
Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник — прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?

a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.

Как проверить угол с помощью египетского треугольника?

Отмерьте на одной стене отрезок длиной 3 метра, а на другой — отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.

Как отмерить угол, используя рулетку

Можно самостоятельно смастерить угольник для замера углов:

1. Соединяем две рейки одна перпендикулярно другой.
2. Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
3. Прибиваем третью рейку к одной отметке.
4. Измеряем гипотенузу, прибиваем рейку ко второй метке.
5. Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
6. Обрезаем лишние концы.

Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.

Источник

О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Важно! Принято считать, что толчком к открытию этой геометрической фигуры послужило путешествие Пифагора в Африку, где он увидел египетские пирамиды. Возможно, именно они стали прообразом данной конструкции.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника.

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

1. 5,
2. 4,
3. 3.

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках.

Итоги

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.

Египетский треугольник

Мы уже много раз обсуждали вопрос, почему так подробно изучаем именно треугольник (минимальная замкнутая ломаная, на треугольники можно разбить любой многоугольник и т. д.).

Но среди треугольников тоже можно выделить несколько особых видов, которые представляют особый интерес. Мы уже говорили о равнобедренном треугольнике (см. рис. 1) и его частном случае – равностороннем (см. рис. 2), а также о прямоугольном треугольнике (см. рис. 3).

Рис. 1. Равнобедренный треугольник

Рис. 2. Равносторонний треугольник

Рис. 3. Прямоугольный треугольник

Сегодня мы будем подробно изучать свойства именно прямоугольных треугольников. С прямыми углами мы сталкиваемся сплошь и рядом: угол парты, ноутбука, дома – этот ряд можно продолжать очень долго.

Прямой угол действительно особенный. Две прямые при пересечении образуют две пары углов, и почти всегда в одной паре углы больше, чем в другой (см. рис. 4). Кроме одного случая – если прямые пересекаются под прямым углом (рис. 5).

Рис. 4. При пересечении двух прямых образуются две пары углов, и почти всегда в одной паре углы больше, чем в другой

Рис. 5. Две прямые пересекаются под прямым углом

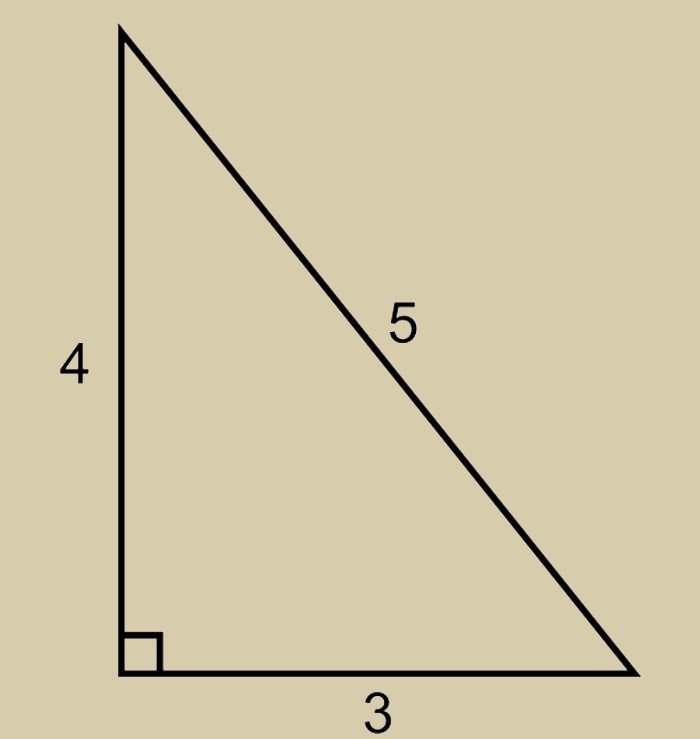
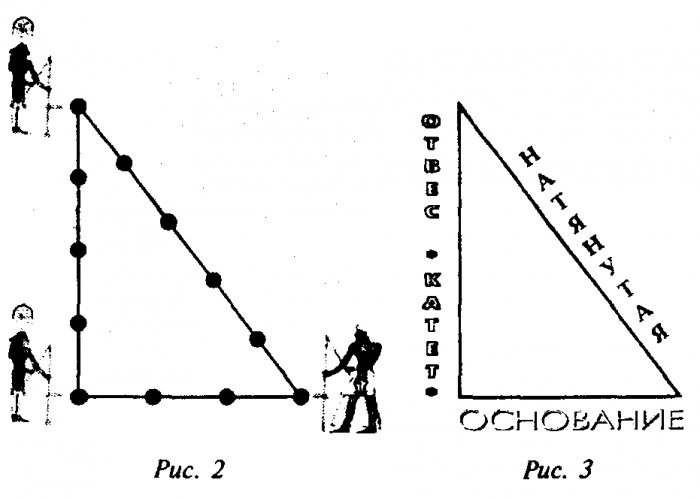
Понятно, что стена дома, чтобы он не упал, должна стоять перпендикулярно фундаменту (под прямым углом к нему) (см. рис. 6). Поэтому еще в древности остро стоял вопрос построения прямого угла. И неоценимую помощь в этом оказал прямоугольный треугольник.Древние египтяне знали, что если длины сторон треугольника образуют пропорцию , то такой треугольник будет прямоугольным. Его так сейчас и называют – египетским (см. рис. 7).

Рис. 6. Чтобы дом не упал, стена дома должна стоять перпендикулярно фундаменту

Рис. 7. Египетский треугольник

Как построить прямой угол?

Как же египтяне использовали свойства египетского треугольника на практике? Рассмотрим один из возможных способов. Возьмем веревку и разделим ее на  равных частей (можно с помощью линейки отмерять кусок веревки длиной ) (см. рис. 8).

Рис. 8. Веревку разделили на  равных частей

Соединим концы веревки друг с другом (рис. 9).

Рис. 9. Концы веревки соединили друг с другом

Вобьем в землю два колышка на расстоянии  друг от друга. Натянем между ними веревку (см. рис. 10).

Рис. 10. Веревку растянули между колышками, вбитыми в землю на расстоянии  друг от друга

Дальше наша задача – с помощью третьего колышка найти такую точку, чтобы веревка оказалась натянутой и оставшиеся две стороны получившегося треугольника оказались равными  и  (см. рис. 11). В результате мы получим прямой угол (см. рис. 12).

Рис. 11. С помощью третьего колышка нашли такую точку, чтобы веревка оказалась натянутой

Рис. 12. В результате получили прямой угол и стороны, равные

Теорема Пифагора

Конечно, египетский треугольник не единственный пример прямоугольного треугольника. Можно, например, построить прямоугольный треугольник, у которого один катет длиннее другого в  раз (см. рис. 13).

Рис. 13. Прямоугольный треугольник, где один катет длиннее другого в  раз

Но можно ли все-таки выделить в египетском треугольнике какое-то свойство, которое «делает его прямоугольным»? Заметим, что числа ,  и  связаны следующим соотношением:

Т. е. сумма квадратов двух меньших сторон равна квадрату большей стороны. Может быть, это и есть то самое искомое свойство прямоугольного треугольника? Проверим.

Построим прямоугольный треугольник, например, с катетами  и . Проведем гипотенузу и попробуем измерить ее длину. Получилось примерно  (см. рис. 14).

Рис. 14. У прямоугольного треугольника с катетами  и  гипотенуза примерно равна

Проверяем нашу гипотезу:

Получились очень близкие значения. Похоже, что разница только в погрешности измерений.

Итак, у нас есть гипотеза: если треугольник прямоугольный, то сумма квадратов его меньших сторон (катетов) равна квадрату гипотенузы. Сейчас мы докажем, что это верное утверждение.

Первое доказательство этого факта приписывается Пифагору (см. рис. 15). Поэтому утверждение так и называется – теорема Пифагора.

Рис. 15. Пифагор

Существует более сотни доказательств, мы рассмотрим одно из самых популярных.

Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (см. рис. 16).

Рис. 16. В прямоугольном треугольнике квадрат гипотенузы  равен сумме квадратов катетов  и :

Доказательство.

Достроим треугольник до квадрата следующим образом (см. рис. 17).

Рис. 17. Построение квадрата при помощи прямоугольных треугольников

Его сторона равна  (см. рис. 18). Площадь этого большого квадрата равна .

Рис. 18. Квадрат со стороной , и площадью

С другой стороны, площадь этого квадрата можно посчитать как сумму площадей четырех треугольников и маленького квадрата. Площадь каждого из прямоугольных треугольников равна , площадь маленького квадрата равна .

Приравнивая площади, получаем:

Теорема доказана.

Теорема, обратная теореме Пифагора

Теорема Пифагора – это свойство прямоугольного треугольника: если треугольник прямоугольный, то у него обязательно квадрат одной стороны равен сумме квадратов двух других.

Работает ли это соотношение как признак, т. е. в обратную сторону? Можно ли утверждать, что если в треугольнике сумма квадратов двух сторон равна квадрату третьей стороны, то он прямоугольный? Или другая эквивалентная формулировка того же утверждения: можно ли утверждать, что не существует непрямоугольных треугольников, у которых квадрат одной стороны равен сумме квадратов двух других? Обратная теорема Пифагора тоже верна. Давайте докажем это.

Теорема, обратная теореме Пифагора: дан треугольник , в котором . Доказать, что  (см. рис. 19).

Рис. 19. Треугольник, в котором квадрат гипотенузы  равен сумме квадратов катетов  и :

Доказательство.

Построим еще один треугольник . Для этого начертим отрезки  и  под прямым углом: . Соединим . Получим прямоугольный треугольник, у которого две стороны равны двум сторонам исходного (см. рис. 20).

Рис. 20. Треугольник , где стороны ,  начерчены под прямым углом

По теореме Пифагора, квадрат гипотенузы нового треугольника равен сумме квадратов его катетов:

Но это же условие выполняется и для стороны  первого треугольника:

Значит:

Но тогда треугольники  и  равны по трем сторонам (третий признак равенства треугольников). Значит, равны и их углы, в частности:

Т. е. треугольник  тоже прямоугольный.

Теорема доказана.

Прямая и обратная теоремы Пифагора – это мощные и часто используемые геометрические инструменты, которые позволяют решить огромное количество задач.

Но вместе с тем, несмотря на широкую известность, теорема Пифагора является всего лишь частным случаем более общей теоремы (теоремы косинусов), которая позволяет, зная три стороны треугольника, не просто определить, есть ли в этом треугольнике прямой угол или нет, а найти величину углов треугольника. Подробнее о ней мы поговорим на следующем уроке.

Тригонометрия

Расстояние можно измерять в единицах длины (100 км), а можно, например, в единицах времени (2 дня пути) (см. рис. 21).

Рис. 21. Расстояние между точками  и  можно измерять по-разному

В зависимости от задачи удобными могут оказаться те или иные способы и единицы измерения. Например, расстояние между точками  и  всего пара километров, но машина преодолеет его не меньше чем за 15 минут (см. рис. 22).

Рис. 22. Расстояние между точками  и  всего пара километров, но машина преодолеет его не меньше чем за 15 минут

Мы умеем измерять углы в градусах. Для этого можно использовать специальный инструмент – транспортир (см. рис. 23).

Рис. 23. Транспортир

Поскольку градус – это  часть окружности, то градусная мера угла фактически показывает, какую часть от полного круга он составляет (см. рис. 24).

Рис. 24. Градусная мера угла, показывает, какую часть от полного круга угол составляет

Но это не всегда удобно. Рассмотрим такой пример: третий признак равенства треугольников (по трем сторонам) говорит нам о том, что любой треугольник однозначно задается длинами трех своих сторон. Но тогда, зная длины сторон треугольника  мы должны уметь находить и его углы.

Т. е. углы можно измерять и с помощью линейки. Как это делать? Вспомним еще один признак – признак подобия треугольников (по двум углам): если у треугольников равны углы, то эти треугольники подобны. Т. е. при пропорциональном увеличении или уменьшении длин сторон треугольника углы не меняются (см. рис. 25). Напрашивается вывод: углы могут быть как-то связаны с отношениями длин сторон (т. к. именно отношение не меняется, каким бы ни был коэффициент пропорциональности).

Рис. 25. При пропорциональном увеличении или уменьшении длин сторон треугольника углы не меняются

Раздел математики, который занимается решением задачи измерения углов через измерения длин, называется тригонометрия – (греч.) «измерение треугольников». И в начале его изучения одним из наших главных инструментов будет как раз прямоугольный треугольник.

Тригонометрические функции

Рассмотрим такую практическую задачу: как измерить высоту дома (или дерева)? На самом деле, существует много способов, рассмотрим один из них. Вытянем руку с поднятым большим пальцем перед собой и будем отходить от дома до тех пор, пока конец пальца не совместится с крышей дома (см. рис. 26).

Рис. 26. Вытянули руку с поднятым большим пальцем перед собой и отошли от дома до тех пор, пока конец пальца не совместился с крышей дома

Зная параметры своего тела и измерив расстояние до дома, можно найти высоту дома:

где  – высота дома,  – длина пальца,  – расстояние от человека до дома,  – длина руки (см. рис. 27).

Рис. 27. Зная параметры своего тела и измерив расстояние до дома, можно найти высоту дома

Как получилась эта формула? Это следствие подобия прямоугольных треугольников с общим острым углом –  и  (см. рис. 28).

Рис. 28. Подобные треугольники  и  с общим острым углом

Действительно, у подобных треугольников стороны пропорциональны, значит:

Для нас сейчас важен следующий вывод: какой бы прямоугольный треугольник с острым углом  мы ни взяли, отношение длин любых двух его сторон будет одинаковым. Действительно, любые два прямоугольных треугольника с равным острым углом будут подобны. Значит, все такие треугольники будут подобны и отношение длин сторон у всех у них будет одинаковым (см. рис. 29).

Рис. 29. Подобные прямоугольные треугольники с равными острыми углами

Получается, что угол  можно определить через отношение длин сторон соответствующего прямоугольного треугольника. Действительно, каждому острому углу  можно поставить в соответствие, например, отношение длины противолежащего ему катета к прилежащему катету прямоугольного треугольника, содержащего этот острый угол (см. рис. 30).

Рис. 30. Каждому острому углу  прямоугольного треугольника можно поставить в соответствие отношение длины противолежащего ему катета к прилежащему

При этом такое отношение будет одинаковым и не будет зависеть от размеров прямоугольного треугольника, а значит, мы получили функцию:

Но мы пока не ответили на другой важный вопрос: можно ли по отношению  однозначно восстановить острый угол ? Действительно, вдруг есть другой прямоугольный треугольник с острым углом , в котором:

Рассмотрим эти два треугольника с углами  и  (см. рис. 31).

Рис. 31. Прямоугольные треугольники , где , и , где

В них равны прямые углы, а стороны, образующие эти прямые углы, пропорциональны:

Тогда эти треугольники подобны, значит, их углы равны, поэтому .

Итак, острый угол прямоугольного треугольника можно однозначно определить через отношение длин сторон этого прямоугольного треугольника.

Мы ввели в качестве примера такую функцию угла – отношение противолежащего катета к прилежащему катету (см. рис. 32). Такая функция называется тангенсом угла:

Рис. 32. Тангенс – отношение противолежащего катета  к прилежащему катету

Понятно, что мы могли ввести обратное отношение – прилежащего катета к противолежащему катету. Такую функцию называют котангенсом угла:

Поскольку в подобных треугольниках пропорциональны любые пары сторон, то можно было взять для эквивалентного определения острого угла не только отношение катетов, но и отношение катета и гипотенузы.

Отношение противолежащего катета к гипотенузе называется синусом угла (см. рис. 33):

Рис. 33. Синус – отношение противолежащего катета к гипотенузе

Отношение прилежащего катета к гипотенузе называется косинусом угла (см. рис. 34):

Рис. 34. Косинус – отношение прилежащего катета к гипотенузе

Можно было бы ввести еще две функции: отношение гипотенузы к катетам (они называются секансом и косекансом), но они почти не используются на практике:

Все введенные нами функции имеют общее название – тригонометрические функции.

Значения тригонометрических функций

Найдем значения тригонометрических функций нескольких самых распространенных острых углов (см. рис. 35).

Рис. 35. Прямоугольный треугольник с катетами  и , гипотенузой  и острыми углами  и

Решение этой задачи нам облегчит следующий факт: синус одного острого угла прямоугольного треугольника равен косинусу другого. Аналогично тангенс альфа равен котангенсу бета.

Или по-другому:

Доказать эти утверждения несложно, используя определения и тот факт, что катет, являющийся прилежащим для одного из острых углов, является противолежащим для другого и наоборот.

Начнем с угла . Рассмотрим соответствующий прямоугольный треугольник (см. рис. 36).

Рис. 36. Прямоугольный треугольник с острым углом, равным

Мы знаем, что катет, лежащий против угла в  равен половине гипотенузы. Следовательно, по определению:

Чтобы найти значение остальных функций по определению, нам понадобится длина второго катета. Найдем ее, используя доказанную ранее теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

Откуда:

Тогда:

Для угла  найти значения функций не составит труда, используя формулы, которые мы перед этим доказали:

Или же вы можете сами это сделать, используя определение и уже готовый рисунок (см. рис. 37).

Рис. 37. Прямоугольный треугольник с катетами  и , гипотенузой  и острыми углами  и

Итак:

Рассмотрим теперь угол . Т. к. один острый угол прямоугольного треугольника равен , то и второй тоже равен: . И прямоугольный треугольник является равнобедренным (см. рис. 38).

Рис. 38. Прямоугольный равнобедренный треугольник с катетами, равными

Если катеты этого треугольника равны , то, по теореме Пифагора:

Получаем:

Подведем итог и посмотрим на все значения найденных нами тригонометрических функций (см. рис. 39).

Рис. 39. Значения тригонометрических углов

Понятно, что для нахождения тригонометрических функций углов  мы использовали свойства прямоугольных треугольников с такими острыми углами. А как найти, например, ?

Самый простой способ – нарисовать, используя транспортир, прямоугольный треугольник с таким углом, затем измерить линейкой длины сторон, поделить и получить значение искомой тригонометрической функции.

Однако понятно, что при таком способе измерения погрешность может оказаться достаточно большой (при построении угла, при измерении длин). И при расчете параметров каких-то технических изделий – например, размеров крыла самолета или арочных пролетов моста – погрешность даже в сотые или тысячные может привести к катастрофическим результатам. Поэтому были придуманы более точные способы вычисления значений тригонометрических функций. Подробнее об этом можно узнать ниже.

Как вычислили значения тригонометрических функций?

Для вычисления точных значений различных функций в математике используют приближение – как кривую можно сколь угодно точно приблизить ломаной, так и функции можно приближать другими функциями, с которыми у них совпадают значения, но которые легче вычислить (см. рис. 40). Обычно в качестве таких функций используют многочлены.

Рис. 40. Приближение функции другой функцией

Например, оказалось, что:

Чтобы доказать это утверждение, школьной математики недостаточно, поэтому примем его на веру, но попробуем проверить.

Только надо помнить, что  здесь измеряется не в градусах, а в радианах (Углы и отрезки. Измерения).

Рассмотрим, например, :

Получаем:

Чем больше слагаемых будем брать, тем точнее получится результат. Если остановимся на первом, получим:

Близко к , но погрешность довольно большая.

Если учтем второе слагаемое, получим:

Уже гораздо ближе.

Если третье, то:

Т. е. с точностью до десятитысячных приближенное значение совпадет с абсолютным.

Такое приближение функции бесконечным многочленом называется разложением в ряд. Использование рядов позволяет с любой точностью вычислять значения самых разных функций.

Для нас же важен результат: если мы знаем угол, то можем найти значение любой тригонометрической функции этого угла. И наоборот, зная значение тригонометрической функции, мы можем найти величину соответствующего острого угла. Раньше для этого использовали специальные таблицы – таблицы Брадиса (см. рис. 41) – или особые инженерные калькуляторы, а сейчас это можно сделать с помощью калькулятора почти в любом мобильном телефоне.

Рис. 41. Таблица Брадиса

Вычисление длин сторон и градусной меры углов прямоугольного треугольника

Может возникнуть вопрос: мы ввели тригонометрические функции, умеем вычислять их значения – и как это поможет нам измерять углы? Зачем они вообще нужны? Предположим, что мы знаем острый угол и сторону прямоугольного треугольника. Раньше по этим данным мы бы не могли найти длины остальных сторон (кроме частных случаев – когда треугольник равнобедренный с углами по  или когда в нем есть угол  градусов). Теперь это сделать несложно.

Рассмотрим конкретный пример: дан треугольник с углом  и гипотенузой  (см. рис. 42).

Рис. 42. Прямоугольный треугольник с углом  и гипотенузой

Найдем длины катетов этого треугольника. Используем определение синуса:

Откуда:

Второй катет можно найти либо используя определение косинуса, либо используя теорему Пифагора.

Кроме того, зная длины сторон прямоугольного треугольника, теперь мы умеем вычислять значения его углов. Например, в египетском треугольнике, о котором мы говорили в начале урока, стороны равны  (см. рис. 43). Найдем острые углы этого треугольника.

Рис. 43. Египетский треугольник

Синус угла, который лежит против катета с длиной , равен:

Осталось найти, какому острому углу соответствует этот синус. Для этого в калькуляторе нужно использовать функцию, обратную вычислению синуса:

Значит, второй острый угол будет равен приблизительно:

Заключение

Из рассмотренных примеров становится понятно, почему этот раздел называется тригонометрия – измерение треугольников. С помощью тригонометрических функций мы можем вычислять неизвестные нам элементы треугольников. Пока мы научились это делать для прямоугольных треугольников. На следующем уроке мы расширим применение тригонометрических функций и для произвольных треугольников.

Список литературы

1. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 8 класс. Учебник. –М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «webmath.ru» (Источник)
2. Интернет-портал «treugolniki.ru» (Источник)
3. Интернет-портал «yaklass.ru» (Источник)

Домашнее задание

1. Боковая сторона равнобедренного треугольника равна , а основание равно . Найти длину высоты, проведенную к основанию.
2. В треугольнике  стороны , . Высота , опущенная на сторону , равна . Найти длину стороны  и градусную меру .
3. В прямоугольном треугольнике гипотенуза равна , а один их острых углов равен . Выразить второй острый угол и катеты через  и .