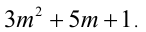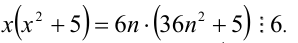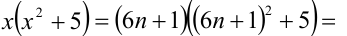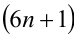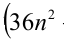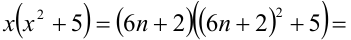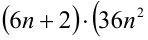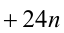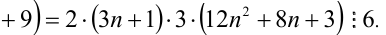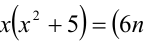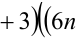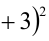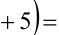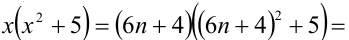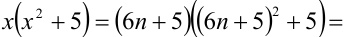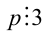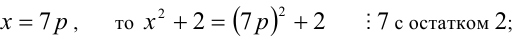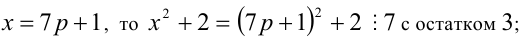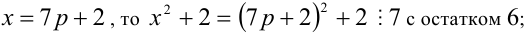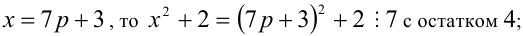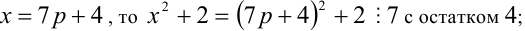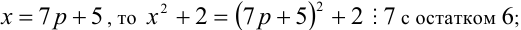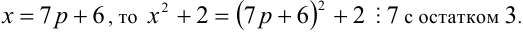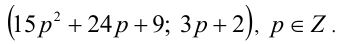© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
19. Задачи на теорию чисел
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Найти остаток от деления числа
Задание
1
#2202
Уровень задания: Легче ЕГЭ
Найдите все числа, при делении которых на (5) в частном получится то же число, что и в остатке.
Пусть при делении числа (a) на (5) в частном получится то же число, что и в остатке. Тогда (a=5r+r). Так как (r) – это остаток при делении на (5), то (r) может быть равно только (0), (1), (2), (3) или (4). Для всех значений (r) найдем соответствующее значение (a): (0), (6), (12), (18), (24).
Ответ:
(0), (6), (12), (18), (24)
Задание
2
#2203
Уровень задания: Легче ЕГЭ
Найдите все числа, при делении которых на (8) в частном получится то же число, что и в остатке.
Пусть при делении числа (a) на (8) в частном получится то же число, что и в остатке. Тогда (a=8r+r). Так как (r) – это остаток при делении на (8), то (r) может быть равно только (0), (1), (2), (3), (4), (5), (6) или (7). Для всех значений (r) найдем возможное значение (a): (0), (9), (18), (27), (36), (45), (54), (63).
Ответ:
(0), (9), (18), (27), (36), (45), (54), (63)
Задание
3
#2204
Уровень задания: Легче ЕГЭ
Число при делении на (8) дает остаток (5). Какой остаток оно дает при делении на (4)?
Пусть число (a) при делении на (8) дает остаток (5), тогда (a=8b+5=8b+4+1=4(2b+1)+1), тогда (a) при делении на (4) дает остаток (1).
Ответ:
(1)
Задание
4
#2205
Уровень задания: Легче ЕГЭ
Докажите, что если числа (a) и (b) дают при делении на (c) одинаковые остатки, то ((a-b), vdots ,c).
Исходя из условия: (a=n_1c+r) и (b=n_2c+r Rightarrow
a-b=n_1c+r-n_2c-r=c(n_1-n_2) , vdots , c).
Ответ:
Доказательство
Задание
5
#2206
Уровень задания: Легче ЕГЭ
Докажите, что среди любых (n+1) натуральных чисел найдутся два, разность которых делится на (n).
Всего при делении на (n) существует (n) различных остатков, а так как чисел (n+1), то по принципу Дирихле найдутся (2) числа с одинаковыми остатками, следовательно, их разность будет делиться на (n).
Ответ:
Доказательство
Задание
6
#2207
Уровень задания: Легче ЕГЭ
Докажите, что числа вида (n^2), где (ninmathbb{N}), не могут при делении на 3 давать остаток (2).
Остаток от деления на число (k) произведения натуральных чисел (Acdot B) равен остатку от деления на число (k) произведения (acdot b), где (a) и (b) – остатки от деления на (k) чисел (A) и (B) соответственно.
Таким образом, остаток от деления числа [(3m + 1)^2 = (3m + 1)cdot (3m + 1)] на (3) равен остатку от деления (1cdot 1) на (3), то есть равен (1).
Остаток от деления числа [(3m + 2)^2 = (3m + 2)cdot (3m + 2)] на (3) равен остатку от деления (2cdot 2) на (3), то есть равен (1).
Остаток от деления числа [(3m)^2 = 9m^2] на (3) равен (0).
Так как любое натуральное число (n) всегда можно представить в одном из видов: (3m), (3m + 1), (3m + 2) ((minmathbb{N}cup{0})), то (n^2) при делении на (3) не может давать в остатке (2).
Ответ:
Доказательство
Задание
7
#2208
Уровень задания: Легче ЕГЭ
При каких простых (p) число (p^2 + 29) также является простым?
Проверим, каким может быть остаток от деления числа (p^2 + 29) на (3):
1) Если (p) не делится на (3), то (p^2) при делении на (3) даёт остаток (1), тогда (p^2 + 29) при делении на (3) даёт такой же остаток, как и число (1 + 29 = 30), то есть (0).
Таким образом, если (p) не делится на (3), то (p^2 + 29) делится на (3), но (p^2 + 29 > 3), а простых чисел, делящихся на (3), кроме числа (3), не бывает.
2) Единственное простое число, которое делится на (3) – это число (3), следовательно, осталось проверить только случай (p = 3): [p^2 + 29 = 9 + 29 = 38] – не является простым.
В итоге мы доказали, что не существует простых чисел (p), таких, что число (p^2 + 29) – простое.
Ответ:
(varnothing)
В ЕГЭ по математике часто встречается задание — найти наименьший остаток от деления натурального числа на 9, 2, 3 и другие цифры. Как показывает практика, многие школьники не справляются с примерами подобного типа. Значительное затруднение вызывают большие числа, поэтому данной тематике стоит уделить особое внимание. Сайт «Школково» поможет подготовиться к итоговому тестированию и с легкостью решать задачи профильного уровня.
Сдайте аттестационное испытание успешно с помощью нашего образовательного портала!
Подготовка к Единому государственному экзамену может стать увлекательной и легкой с удобным онлайн-сервисом «Школково». На нашем сайте вы найдете все необходимые для повторения материалы, а также множество уравнений для вычисления, база которых постоянно обновляется и дополняется. Вся информация тщательно подобрана, систематизирована и изложена в наиболее простой и понятной форме нашими преподавателями. Благодаря подобному подходу выпускники усваивают материал в более короткие сроки по сравнению с обучением по школьному пособию, и найти остаток от деления числа на 4, 2 и 3 для них не составляет труда.
В разделе «Теоретическая справка» собраны правила и формулы. Они пригодятся для выполнения упражнений на тему нахождения остатка от деления суммы двух чисел на 7, 4, 5 и другие цифры. В «Каталогах» представлено множество задач различного уровня сложности. Ученики могут выбрать любое упражнение из предложенных. Если оно вызовет затруднения, на нашем сайте есть раздел «Избранное». Туда можно добавить сложные и интересные задачи, к которым вы хотели бы вернуться позже.
Для того чтобы занятия проходили наиболее эффективно, рекомендуем начать с простых заданий. Так вы проверите свои способности и выявите слабые стороны, на которые стоит обратить особое внимание. Если после решения нескольких простых уравнений на деление числа без остатка на 5, 4, 2 и другие цифры вы поняли, что они даются вам легко, сразу переходите к более трудным задачам. Всего через несколько дней вы подтяните знания в данной тематике и будете справляться с упражнениями любого уровня сложности.
Чтобы занятия приносили результат, советуем обращаться к нашему порталу ежедневно. Зарегистрируйтесь на сайте для сохранения прогресса. Каждый день вы будете получать индивидуальное задание, основанное на ваших способностях. Постепенно уравнения будут становиться все труднее, поэтому вы незаметно для себя научитесь решать даже сложные варианты, где нужно найти отрицательные числа.
Начните занятия на сайте «Школково» уже сегодня, и результат не заставит себя ждать!
Обучение на нашем портале доступно каждому желающему. Чтобы отслеживать прогресс и получать новые задания на нахождение остатка при делении числа на 100, созданные персонально для вас, зарегистрируйтесь в системе. Желаем удачной подготовки!

УСТАЛ? Просто отдохни
Онлайн калькулятор определит остаток от деления чисел, поможет проверить себя при решении уроков и примеров на деление. Деление с остатком (деление по модулю) — это арифметическая операция, в результате выполнения которой получается два целых числа: неполное частное и остаток от деления.
Остаток всегда должен быть меньше делителя. Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
Метод анализа остатков
В основе метода анализа остатков, который используется при решении ряда задач с целочисленными неизвестными, лежит формула деления с остатком. Суть метода состоит в рассмотрении случаев различных остатков от деления на заданное число, что позволяет в конечном итоге решить поставленную задачу.
В первых трёх примерах, приведённых ниже, в явном виде ищутся остатки от деления одних целых чисел на другие.
Пример №19.
Найти частное и остаток от деления числа (— 23) на 7.
Решение:
Согласно формуле деления с остатком, получаем:
— 23 = — 4 • 7 + 5 , т.е. частное равно — 4, а остаток равен 5.
Пример №20.
Найти сумму остатков, получающихся при делении числа 7263544587435873 на 2, 4, 5, 9, 10, 25.
Решение:
Используя признаки делимости нацело на числа 2,4,5,9,10 и 25, находим остатки:
- остаток от деления на 2 равен 1;
- остаток от деления на 4 равен 1;
- остаток от деления на 5 равен 3;
- остаток от деления на 9 равен 0;
- остаток от деления на 10 равен 3;
- остаток от деления на 25 равен 23.
Суммируя остатки 1 + 1+3+0+3+23, получаем в ответе 31.
Пример №21.
Пусть остаток от деления натурального числа m на 7 равен 3. Найти остаток от деления на 7 числа
Решение:
Из условия следует, что число m имеет вид: 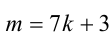
Таким образом, остаток от деления числа 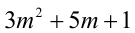
Пример №22.
Доказать, что при любых целых X число 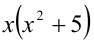
Решение:
Разобьём множество всех целых X на 6 групп в зависимости от остатка при делении на 6, т.е. рассмотрим 6 случаев:
1) Пусть 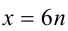
2) Пусть 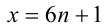
3) Пусть 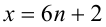
4) Пусть 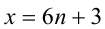
5) Пусть 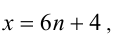
6) Пусть 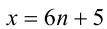
Таким образом, мы рассмотрели все целые числа X и доказали, что всегда (в каждом из шести случаев) выражение 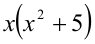
Замечание. Эту задачу можно было решить иначе. Преобразуем данное в условии задачи выражение:
Каждое из двух слагаемых делится нацело на 6 (первое как произведение трёх последовательных целых чисел), поэтому их сумма кратна 6.
Пример №23.
Учительница принесла в класс счётные палочки. Дети раскладывали их в пакетики. Когда разложили по 2 палочки в каждый пакетик, то осталась 1 лишняя палочка. Затем разложили по 13 штук в пакетик, и тогда осталось 7 лишних палочек. Когда же палочки разложили по 9 штук в пакетик, то лишних не осталось. Сколько, самое меньшее, было счётных палочек?
Решение:
Пусть всего было n счётных палочек. Тогда условия задачи приводят к системе
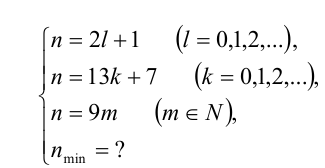
Таким образом, требуется найти наименьшее натуральное нечётное число п , делящееся на 9 и дающее при делении на 13 остаток 7. Заметим, что в силу нечётности 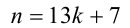
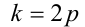
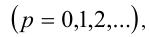
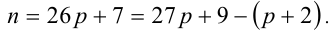
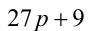
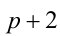
Ответ: самое меньшее — 189 счётных палочек.
Пример №24.
После деления некоторого двузначного числа на сумму его цифр получается 7 и в остатке 6. После деления этого же двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найти это двузначное число.
Решение:
Обозначим 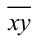
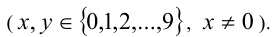
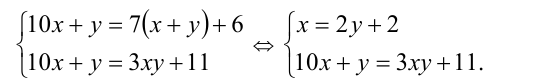
Решая систему методом подстановки, находим единственное решение, удовлетворяющее всем условиям задачи: x= 8, y = 3 . Ответ: 83.
Пример №25.
Целые числа m, n,k не делятся нацело на 3. Доказать, что число 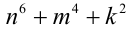
Доказательство. Если 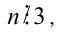
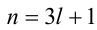
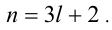
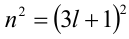
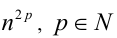
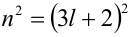
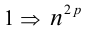
Пример №26.
Доказать, что если 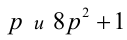
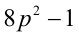
Доказательство. Если 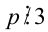
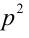
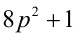
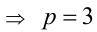
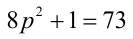
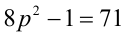
Пример №27.
Решить уравнение в целых числах
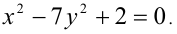
Решение:
Перепишем уравнение в виде: 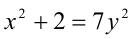
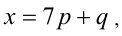
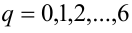
1) Если
2) если
3) если
4) если
5) если
6) если
7) если
Итак, правая часть уравнения делится на 7 нацело (т.е. с остатком 0), а левая часть при этом — с остатками 2, 3, 4, 6. Однако равные числа при делении на одно и то же целое число 7 должны давать одинаковые остатки. Полученное противоречие говорит о том, что данное уравнение не имеет решений в целых числах.
Пример №28.
Найти все пары целых чисел (x;y), удовлетворяющие уравнению
и доказать, что для каждой такой пары сумма 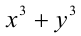
Решение:
Заметим, что левая часть уравнения кратна 3, следовательно, и правая часть должна делиться на 3 нацело. Разобьём множество всех целых y на три группы в зависимости от остатка при делении на 3:
1) Если 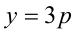
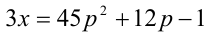
2) Если 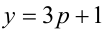
3) Наконец, если 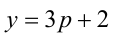
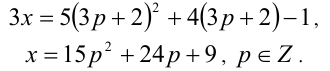
Следовательно, общий вид решений: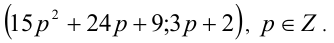
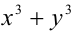
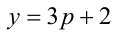
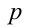
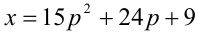
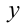
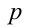


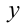
Ответ:
Пример №29.
Решить в целых числах уравнение
Решение:
Так как произвольное целое число 
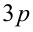
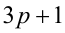
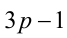
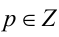
то любое число в кубе или делится нацело на 9, или даёт при делении на 9 в остатке 1 или 8. Аналогично, так как 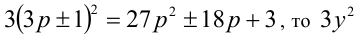
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны: