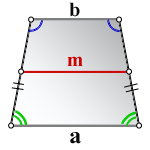
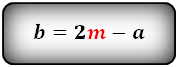
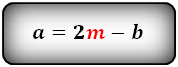
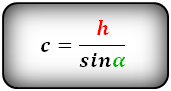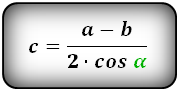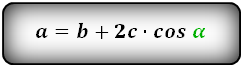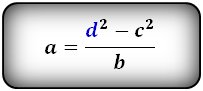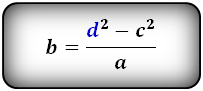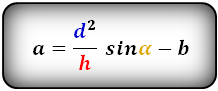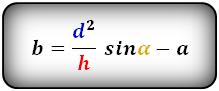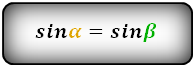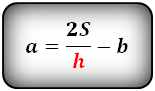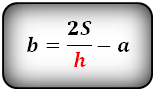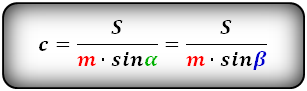1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
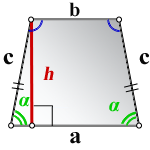
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
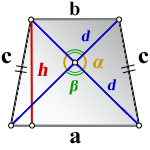
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
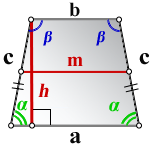
4. Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 08 октября 2013
-
Обновлено: 13 августа 2021
Длинное основание равнобедренной трапеции с заданной высотой Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 2D геометрия ↺ | |
| 2D геометрия | Равнобедренная трапеция ↺ | |
| Равнобедренная трапеция | Ребра равнобедренной трапеции ↺ | |
| Ребра равнобедренной трапеции | Длинное основание равнобедренной трапеции ↺ |
|
✖Короткое основание равнобедренной трапеции — это самая короткая сторона среди пары параллельных сторон равнобедренной трапеции.ⓘ Короткое основание равнобедренной трапеции [BShort] |
+10% -10% |
||
|
✖Высота равнобедренной трапеции — это перпендикулярное расстояние между парой параллельных ребер основания равнобедренной трапеции.ⓘ Высота равнобедренной трапеции [h] |
+10% -10% |
||
|
✖Острый угол равнобедренной трапеции — это любой из углов на более длинном ребре основания, образованный боковыми и непараллельными ребрами равнобедренной трапеции.ⓘ Острый угол равнобедренной трапеции [∠Acute] |
+10% -10% |
|
✖Длинное основание равнобедренной трапеции — это самая длинная сторона среди пары параллельных сторон равнобедренной трапеции.ⓘ Длинное основание равнобедренной трапеции с заданной высотой [BLong] |
⎘ копия |
Длинное основание равнобедренной трапеции с заданной высотой Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Короткое основание равнобедренной трапеции: 9 метр —> 9 метр Конверсия не требуется
Высота равнобедренной трапеции: 4 метр —> 4 метр Конверсия не требуется
Острый угол равнобедренной трапеции: 55 степень —> 0.959931088596701 Радиан (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
14.6016603056798 метр —> Конверсия не требуется
6 Длинное основание равнобедренной трапеции Калькуляторы
13 Ребра равнобедренной трапеции Калькуляторы
Длинное основание равнобедренной трапеции с заданной высотой формула
Длинное основание равнобедренной трапеции = Короткое основание равнобедренной трапеции+(2*Высота равнобедренной трапеции*cot(Острый угол равнобедренной трапеции))
BLong = BShort+(2*h*cot(∠Acute))
Что такое равнобедренная трапеция?
Трапеция – это четырехугольник с одной парой параллельных ребер. Равнобедренная трапеция означает трапецию, у которой пара непараллельных ребер равна. Пара параллельных ребер называется основаниями, а пара непараллельных равных ребер — боковыми ребрами. Углы при длинном основании равны острым углам, а углы при коротком основании равны тупым углам. Кроме того, пары противоположных углов дополняют друг друга. Следовательно, равнобедренная трапеция циклична.
Как найти основания трапеции
Основания трапеции можно найти несколькими способами, в зависимости от заданных параметров. При известной площади, высоте и боковой стороне равнобокой трапеции последовательность расчетов сводится к вычислениям стороны равнобедренного треугольника. А также к использованию свойства равнобокой трапеции.

Инструкция
Начертите равнобокую трапецию. Дана площадь трапеции — S, высота трапеции — h и боковая сторона — a. Опустите высоту трапеции на большее основание. Большее основание будет разделено на отрезки m и n.

Для определения длины обоих оснований (х, y) примените свойство равнобокой трапеции и формулу расчета площади трапеции.
Согласно свойству равнобокой трапеции отрезок n равен полуразности оснований х и y. Следовательно, меньшее основание трапеции y можно представить в виде разности большего основания и отрезка n, помноженного на два: y = x — 2*n.
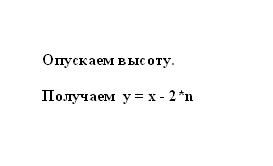
Найдите неизвестный меньший отрезок n. Для этого вычислите одну их сторон получившегося прямоугольного треугольника. Треугольник образован высотой – h (катет), боковой стороной – a (гипотенуза) и отрезком – n (катет). Согласно теореме Пифагора неизвестный катет n² = a² — h². Подставьте известные числовые значения и высчитайте квадрат катета n. Возьмите корень квадратный из полученного значения – это и будет длина отрезка n.
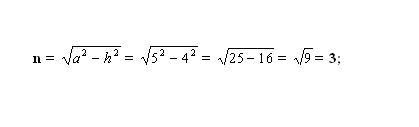
Подставьте полученное значение в первое уравнение для вычисления y. Площадь трапеции высчитывается по формуле S = ((х + y)*h)/2. Выразите неизвестную переменную: y = 2*S/h – х.
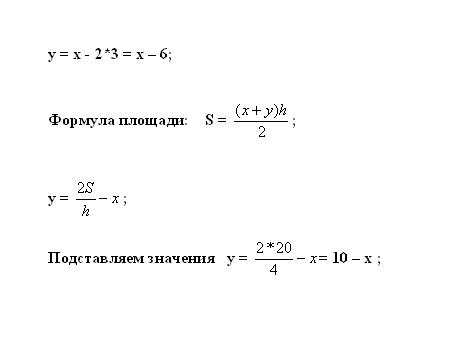
Запишите оба полученных уравнения в систему. Подставляя известные значения, найдите две искомые величины в системе двух уравнений. Полученное решение системы х представляет собой длину большего основания, а y — меньшего основания.

Источники:
- высота равнобокой трапеции
Как найти основания трапеции
Основания трапеции можно найти несколькими способами, в зависимости от заданных параметров. При известной площади, высоте и боковой стороне равнобокой трапеции последовательность расчетов сводится к вычислениям стороны равнобедренного треугольника. А также к использованию свойства равнобокой трапеции.
Начертите равнобокую трапецию. Дана площадь трапеции — S, высота трапеции — h и боковая сторона — a. Опустите высоту трапеции на большее основание. Большее основание будет разделено на отрезки m и n.
Для определения длины обоих оснований (х, y) примените свойство равнобокой трапеции и формулу расчета площади трапеции.
Согласно свойству равнобокой трапеции отрезок n равен полуразности оснований х и y. Следовательно, меньшее основание трапеции y можно представить в виде разности большего основания и отрезка n, помноженного на два: y = x — 2*n.
Найдите неизвестный меньший отрезок n. Для этого вычислите одну их сторон получившегося прямоугольного треугольника. Треугольник образован высотой – h (катет), боковой стороной – a (гипотенуза) и отрезком – n (катет). Согласно теореме Пифагора неизвестный катет n² = a² — h². Подставьте известные числовые значения и высчитайте квадрат катета n. Возьмите корень квадратный из полученного значения – это и будет длина отрезка n.
Подставьте полученное значение в первое уравнение для вычисления y. Площадь трапеции высчитывается по формуле S = ((х + y)*h)/2. Выразите неизвестную переменную: y = 2*S/h – х.
Запишите оба полученных уравнения в систему. Подставляя известные значения, найдите две искомые величины в системе двух уравнений. Полученное решение системы х представляет собой длину большего основания, а y — меньшего основания.
Все формулы сторон равнобедренной трапеции
1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания :
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции :
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь :
Формулы трапеции
Для расчёта всех основных параметров трапеции воспользуйтесь калькулятором.
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
- Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме $$ FE = $$
- Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
- Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е. $$ KL = $$
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции
- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Формулы площади произвольной трапеции
Площадь трапеции через основания и высоту
Площадь трапеции через среднюю линию и высоту
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через четыре стороны
Формулы площади равнобедренной трапеции
Площадь трапеции через стороны
Площадь трапеции через стороны и угол
$$ S = AD * sin(∠ADC) * (DC — AD * cos(∠ADC)) $$ $$ S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC)) $$
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$ S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB) $$
Площадь трапеции если в нее вписана окружность
Формулы сторон произвольной трапеции
Основание через другое основание и среднюю линию
$$ AB = 2 * FE — DC $$ $$ DC = 2 * FE — AB $$
Основание через другое основание, диагонали и угол между ними
$$ DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ AB = DC — AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD) $$ $$ AB = DC — AD * cos(∠ADC) — BC * cos(∠BCD) $$ $$ AD = $$ $$ BC = $$
Формулы сторон равнобедренной трапеции
$$ AD = $$ $$ AD = $$ $$ DC = AB + 2 * AG * ctg(∠ADC) $$ $$ AB = DC — 2 * AG * ctg(∠ADC) $$ $$ DC = AB + 2 * AB * cos(∠ADC) $$ $$ AB = DC — 2 * AB * cos(∠ADC) $$
Длина основания через диагональ, боковую сторону и другое основание
Длина боковой стороны через диагональ и основания
Длина основания через высоту, другое основание, диагонали и угол между ними
Длина основания через высоту, другое основание и площадь трапеции
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
Длина боковой стороны через площадь трапеции, основания и угол при основании
Формулы сторон прямоугольной трапеции
$$ DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD) $$ $$ AB = DC — BC * cos(∠BCD) = DC — AD * ctg(∠BCD) $$ $$ DC = AB + sqrt $$ $$ AB = DC — sqrt $$
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG) $$ DC = <2 * S over AD>- AB $$ $$ AB = <2 * S over AD>- DC $$
Формулы диагоналей произвольной трапеции
Длина диагоналей через четыре стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту
Длина диагоналей через стороны и другую диагональ
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
Формулы диагоналей равнобедренной трапеции
Длина диагоналей через стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту основание и угол при основании
Длина диагоналей через сторону и высоту
Формулы диагоналей прямоугольной трапеции
Формулы средней линии произвольной трапеции
Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и высоту
Формулы средней линии равнобедренной трапеции
Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
$$ FE = DC — AG * ctg(∠ADC) = AB + AG * ctg(∠ADC) $$
Длина средней линии через основания, боковую сторону и высоту
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и боковую сторону
Формулы средней линии прямоугольной трапеции
Длина средней линии через основания, высоту и угол при нижнем основании
Длина средней линии через основания, боковую сторону и угол при нижнем основании
Длина средней линии через основания и боковые стороны
Длина средней линии через диагонали, высоту и угол между диагоналями
Формулы высоты произвольной трапеции
Длина высоты через четыре стороны
Длина высоты через боковую сторону и прилегающий угол к основанию
$$ AG = AD * sin(∠ADC) = BC * sin(∠BCD) $$
Длина высоты через диагонали и углы между ними
Длина высоты через среднюю линию, диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы высоты равнобедренной трапеции
Длина высоты через по сторонам
Длина высоты через боковую сторону и прилегающий угол к основанию
Длина высоты через основания и прилегающий угол к основанию
Длина высоты через диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы боковых сторон прямоугольной трапеции
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
Сторона BC через основания и угол ∠BCD
Сторона BC через Сторону AD
Сторона BC через площадь, среднюю линию и угол ∠BCD
Сторона BC через площадь, основания и угол ∠BCD
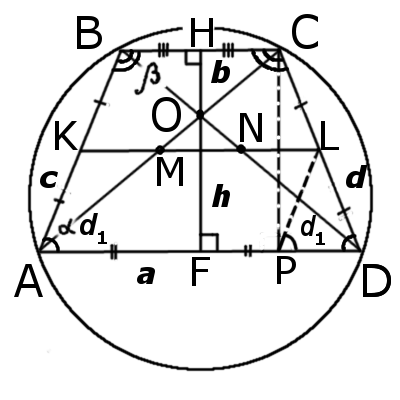
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
 |
| Рис.1 |
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
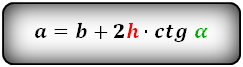
a = b + 2 h ctg α = b + 2 c cos α
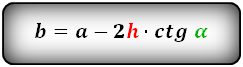
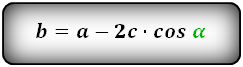
b = a — 2 h ctg α = a — 2 c cos α
| c = | h | = | a — b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 — c 2 | b = | d 1 2 — c 2 | c = √ d 1 2 — ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | — b b = | 2S | — a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
m = a — h ctg α = b + h ctg α = a — √ c 2 — h 2 = b + √ c 2 — h 2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 — ( a — b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a — b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
d 1 = √ a 2 + c 2 — 2 ac cos α
d 1 = √ b 2 + c 2 — 2 bc cos β
4. Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √ 4 c 2 — ( a — b ) 2 |
| 4 |
2. Формула площади через стороны и угол:
S = ( b + c cos α ) c sin α = ( a — c cos α ) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
a — большее основание
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://calc-online24.ru/formula/trapez
http://ru.onlinemschool.com/math/formula/trapezium_isosceles/