План урока:
Что такое степени?
Основание и показатель
Квадрат числа
Куб числа
Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь.
М.В.Ломоносов
Что такое степени?
Начиная с первого класса, вы знакомились с несколькими арифметическими действиями, использовали их при решении задач и заданий. Принято считать, что в математике существует 4 основных действия: сложение, вычитание, умножение, деление. Оказывается, существуют и другие действия. Сегодня рассмотрим новое и очень интересное.
Рассмотрим ситуацию.
Дети получили домашнее задание по математике – решить три столбика уравнений, по три уравнения в каждом. Сколько всего уравнений задали детям?
Чтобы ответить на вопрос задачи, суммируем уравнения во всех столбиках. Мы знаем, что в одном столбике три уравнения, а в трех столбиках:
3+3+3.
В данном случае слагаемое повторяется три раза. Сумму одинаковых компонентов можно заменить произведением. Для этого повторяющуюся составляющую умножаем на количество повторов.
3×3
Составленное произведение запишем короче. Для этого, запомним значение множителей, количество множителей.
Сначала, записываем значение множителя. Рядом с записанной цифрой, записываем их численность.
Получается: 32
То есть: 3+3+3=3×3=32=9.
Получен ответ на главный вопрос задачи. Ученикам задали девять уравнений.
Решая задачу, мы познакомились с новым математическим действием — возведением в степень.
Давайте дадим правильное определение рассмотренному действию.
Степень числа – это произведение одинаковых множителей, взятых определенное количество раз: 𝑎 × 𝑎 × 𝑎 …= 𝑎b .
Произносят: а в степени б.
К примеру, запись 64, нужно читать: «шесть в четвертой степени», «четвертая степень шести».
Разберем еще одну задачу.
Работникам городского парка необходимо засеять травой клумбу прямоугольной формы. Чтобы правильно рассчитать необходимое количество семян, нужно знать посадочную площадь. Найдите площадь клумбы, зная, что её ширина и длина по четыре метра.
Чтобы ответить на главный вопрос, вспомним, правило нахождения площади прямоугольника: для нахождения площади прямоугольника необходимо длину умножить на ширину. Зная длину и ширину клумбы, найдем произведение:
Получим, 4×4 – площадь клумбы.
В данном произведении составляющая четыре, использована два раза. На основании изученного определения рассматриваемое произведение запишем иначе:
Посадочная площадь клумбы равна 16 м2.
Основание и показатель
Математика – точная наука. Каждый компонент имеет определенное наименование, определенное место. Давайте вспомним наименования составляющих в различных математических действиях:
Источник
У изученного действия, составляющие имеют свои отличные от других наименования. Их называют: основание и показатель.
Запишем правильную формулировку для составляющих рассмотренного действия.
Числовое значение дублирующейся составляющей, называют основанием степени.
Цифра, стоящая справа, обозначает, численность повторяющихся множителей,называется показателем степени
Источник
В выражении 89, основанием является 8, а показателем 9. Значит, чтобы найти значение рассматриваемого выражения, нужно умножить число 8 само на себя 9 раз.
Найдем значение выражения 55.
Для верного проведения необходимых вычислений определим основание (дублирующийся компонент) — пять, и показатель (численность составляющих) – пять.
Имеем:
Исходя из рассмотренных примеров, можно сделать вывод как возвести число в степень:
для возведения числа в степень достаточно это число умножить само на себя несколько раз (на численность повторов указывает показатель степени).
Вычислим: 26
Нам необходимо возвести два в шестую степень. Главное – нужно умножить два, само на себя шесть раз:
Получается, 26=64
Все очень просто! Главное – запомнить, что для возведения числа в степень, нужно умножить его само на себя, а сколько раз это сделать, вам подскажет показатель!
Квадрат и куб числа.
Квадрат числа
На изготовление одного килограмма творога уходит три литра молока. Сколько молока потребуется для изготовления трех килограммов творога?
Чтобы ответить на главный вопрос, мы должны молоко необходимое для изготовления одного килограмма творога, взять три раза, чтобы в результате должно получиться три килограмма творога.
Получим: 3+3+3.
Слагаемое три, взяли три раза, полученную сумму заменим произведением. Для этого числовое значение слагаемых (3) умножаем на количество таких слагаемых (3) – 3×3.
Пользуясь изученным определением, зная, что в произведении множитель три использован два раза, полученное выражение запишем иначе: 32
Выражение 32, произносится «три в квадрате».
3×3=32 =9.
Для изготовления трех килограммов творога потребуется девять литров молока.
Если показатель степени числа равен 2, то говорят « число в квадрате».
42 – четыре в квадрате;
72 – семь в квадрате;
152 – пятнадцать в квадрате.
Важно!
Чтобы возвести число в квадрат, умножаем его само на себя два раза.
Куб числа
В выходной день бабушка пекла пирожки с малиной, клубникой и вишней. До прихода внуков она успела испечь по три пирожка с каждой начинкой. По рецепту пирожков должно получиться в три раза больше, чем выпеченных. Вычислите, сколько пирожков должно получиться по рецепту?
Чтобы понять на сколько пирогов рассчитан рецепт бабушки, нужно знать, сколько пирогов бабуля успела испечь. Мы знаем, что готовы по три штуки с каждой начинкой – малина, клубника, вишня. Поэтому три готовых пирожка повторяем три раза, то есть: 3×3.
Зная сколько выпеченных изделий, можем найти, сколько пирогов получится согласно рецепту. Для этого, готовые пироги увеличиваем в три раза (умножаем на три):
3×3×3.
Мы видим, составляющая три использована три раза. Пользуясь изученным определением, можем записать иначе: 33
Составленное выражение произносится «три в кубе».
Вычислим:
Бабушкин рецепт рассчитан на приготовление 27 пирожков.
Показатель степени числа равен 3, то говорят «число в кубе».
73 – семь в кубе;
93 – девять в кубе;
113 – одиннадцать в кубе.
Запомните:
Чтобы возвести число в куб, его нужно умножить само на себя три раза!
И в заключение урока рассмотрим таблицу, которая станет верным другом на протяжении учебного процесса.
Правила пользования таблицей!
На верхней горизонтальной строке записаны основания, в первом вертикальном столбце – показатели. Для нахождения нужного значения квадрата, куба числа, в верхней строке находим требуемое число и опускаемся на вторую, третью строку (зависит от показателя).
Вот и все! Благодаря табличке, не нужно выполнять вычисления, а просто держать её под рукой!
Интересные факты.
- 1) Человеческий мозг содержит 2×1010 нервных клеток, имеет ежедневную возможность сохранять 8,6×107 бит различной информации. У взрослых людей память хранит множество информации – 1018 бит.
- 2) Ежесекундно человеческий мозг выполняет 105 химических процессов. Сплетение нейронов головного мозга в 1,4×103 раз сложнее, всей мировой сети телефонной связи.
- 3) Все человечество на планете можно поместить в куб, имеющий длину ребра 1 километр.
- 4) Самое маленькое число, состоящее из четырех знаков и являющееся суммой двух кубов натуральных чисел.
- 5) В древние времена славяне использовали своеобразную запись чисел, большого значения.
103 называли «тысяща»;
106 имело название «тьма»
1012 прозвали «легион»
1024 называлось «леодр»
1048 читалось «ворон»
1049 произносили, «колода»
Степень числа
- Возведение в степень
- Выражения со степенями. Порядок действий
- Калькулятор возведения в степень
Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.
Рассмотрим умножение одинаковых чисел, например:
5 · 5 · 5 = 125.
Произведение 5 · 5 · 5 можно записать так: 53 (пять в третьей степени). Выражение 53 — это степень. Следовательно,
5 · 5 · 5 = 53 = 125.
Рассмотрим выражение 53 . В этом выражении число 5 — основание степени, а число 3 — показатель степени.
Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.
Читаются степени так:
- 72 —
семь во второй степени
.Вторую степень числа также называют квадратом этого числа. Следовательно, выражение 72 можно прочесть так:
семь в квадрате
иликвадрат числа семь
. - 23 —
два в третьей степени
.Третью степень числа также называют кубом этого числа. Следовательно, выражение 23 можно прочесть так:
два в кубе
илидва куб
. - 64 —
шесть в четвёртой степени
. - 1015 —
десять в пятнадцатой степени
. - an —
a в энной степени
илиa в степени эн
.
Пример. Записать в виде степени:
a) 5 · 5;
б) 10 · 10 · 10 · 10;
в) 8 · 8 · 8.
Решение:
a) 5 · 5 = 52;
б) 10 · 10 · 10 · 10 = 104;
в) 8 · 8 · 8 = 83.
Возведение в степень
Возведение числа в степень — это вычисление произведения одинаковых множителей. Например, возвести число 2 в третью степень (23) — это значит найти произведение 2 · 2 · 2 , то есть
23 = 2 · 2 · 2 = 8.
Результат возведения в степень называется степенью (также как и само выражение, значение которого вычисляется). В выражении:
23 = 8,
2 — это основание степени, 3 — показатель степени, 8 — степень.
Пример. Вычислите:
a) 112;
б) 25;
в) 104.
Решение:
a) 112 = 11 · 11 = 121;
б) 25 = 2 · 2 · 2 · 2 · 2 = 32;
в) 104 = 10 · 10 · 10 · 10 = 10000.
Выражения со степенями. Порядок действий
Если выражение не содержит скобки и содержит степени, то сначала выполняется возведение в степень в порядке следования степеней (слева направо), а затем все остальные арифметические действия. Если выражение содержит скобки, то сначала выполняются действия в скобках, с учётом всех правил порядка выполнения действий.
Рассмотрим два выражения:
52 + 22
и
(5 + 2)2
В соответствии с порядком выполнения действий в первом случае сначала выполняется возведение в степень, а затем вычисляется сумма. Во втором случае сначала вычисляется сумма, а затем результат возводится в квадрат.
52 + 22 = 25 + 4 = 29,
(5 + 2)2 = 72 = 49.
Пример 1. Найти значение выражения:
5 · (10 — 
Решение: Сначала выполняется действие, заключённое в скобки:
1) 10 — 8 = 2.
Затем, по правилам порядка действий, выполняется возведение в степень:
2) 23 = 2 · 2 · 2 = 8.
И последним действием вычисляется произведение:
3) 5 · 8 = 40.
Ответ: 5 · (10 — 
Пример 2. Вычислить:
a) (4 + 2) · 32;
б) 3 · 52 — 50;
в) 3 · 4 + 62.
Решение:
a) (4 + 2) · 32 = 54
- 4 + 2 = 6
- 32 = 9
- 6 · 9 = 54
б) 3 · 52 — 50 = 25
- 52 = 25
- 3 · 25 = 75
- 75 — 50 = 25
в) 3 · 4 + 62 = 48
- 62 = 36
- 3 · 4 = 12
- 12 + 36 = 48
Калькулятор возведения в степень
Данный калькулятор поможет вам выполнить возведение в степень. Просто введите основание с показателем степени и нажмите кнопку Вычислить
.
Ноль в кубе — так и останется ноль.
Единица в кубе равна самой себе, то есть единице (да она в любой степени равна себе, вот чудо-то!).
Двойка в кубе — это восемь.
Тройка в кубе — двадцать семь.
Четыре в кубе — шестьдесят четыре.
Кубическая пятерка — сто двадцать пять.
Шесть в третьей степени составляет двести шестнадцать.
Семерка, возведенная в куб, выросла до трехсот сорока трех.
Восьмерка, умноженная сама на себя трижды, предстает в наряде пятисот двенадцати.
Девятка, вознесенная в третью степень, превращается в семьсот двадцать девять.
А десятка в кубе, как ни пыжилась, а всего лишь жалкая тысяча.
Задача решена, но, спешу предупредить, это лишь фрагмент одной из многих страниц увлекательного произведения, именуемого «Таблицы брадиса».
Содержание
- Таблица кубов
- Таблица кубов
- Теория
- Скачать таблицу кубов
- Таблица кубов и квадратов, как состовлять и найти
- Как появилось понятие куб числа?
- Степень с натуральным показателем
- Теория
- Возвести в куб онлайн
- Дополнительная информация
- Решение №1633 Объём куба равен 24. Найдите объём треугольной призмы, отсекаемой от куба …
Таблица кубов
Таблица кубов или таблица возведения чисел в третью степень. Интерактивная таблица кубов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 |
| 2 | 8000 | 9261 | 10648 | 12167 | 13824 | 15625 | 17576 | 19683 | 21952 | 24389 |
| 3 | 27000 | 29791 | 32768 | 35937 | 39304 | 42875 | 46656 | 50653 | 54872 | 59319 |
| 4 | 64000 | 68921 | 74088 | 79507 | 85184 | 91125 | 97336 | 103823 | 110592 | 117649 |
| 5 | 125000 | 132651 | 140608 | 148877 | 157464 | 166375 | 175616 | 185193 | 195112 | 205379 |
| 6 | 216000 | 226981 | 238328 | 250047 | 262144 | 274625 | 287496 | 300763 | 314432 | 328509 |
| 7 | 343000 | 357911 | 373248 | 389017 | 405224 | 421875 | 438976 | 456533 | 474552 | 493039 |
| 8 | 512000 | 531441 | 551368 | 571787 | 592704 | 614125 | 636056 | 658503 | 681472 | 704969 |
| 9 | 729000 | 753571 | 778688 | 804357 | 830584 | 857375 | 884736 | 912673 | 941192 | 970299 |
Таблица кубов
Теория
Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Данное выражение читается: «возвести в куб число 6» или «6 в кубе».
Скачать таблицу кубов
- Нажмите на картинку чтобы посмотреть в увеличенном виде.
- Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.
Источник
Таблица кубов и квадратов, как состовлять и найти
Как появилось понятие куб числа?
Древнегреческие математики оперировали так называемыми фигурными числами – числами, которые можно представить в виде фигуры. Выделялись, например:
Кубические числа выделялись в особый вид фигурных чисел, поскольку куб числа x равен объёму куба с длиной ребра, равной x .
Вообще, фигурные числа – интереснейшая тема . Ставьте лайки этому материалу, если хотите узнать о них больше!
Последовательность кубов натуральных чисел выглядит так
Полезно будет запомнить, хотя бы те, что меньше тысячи. Особенно мне нравится число 729. Посмотрите:
- 729 равно 9 в кубе;
- 729 равно 3 в шестой степени;
- 729 равно 27 в квадрате, что очень сильно нравилось пифагорейцам. Например, Платон считал, что количество ночей и дней в году равняется 729 (364, 5 на каждое время суток). Кроме того, он считал, что жизнь царя должна длиться 729 месяцев (около 67 лет).
Еще несколько интересных свойств кубов чисел:
- 1728 является количеством кубических дюймов в кубическом футе;
- 1728 – единственный композиториал , являющийся одновременно кубом числа. Композиториал – это факториал ( о нем я достаточно интересно уже писал ), деленный на праймориал – последовательность произведения простых чисел, меньше данного.
Вот так, к слову выглядит формула вычисления суммы первых кубов чисел:
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
Возвести число в куб — значит умножить его само на себя три раза.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Теория
Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Данное выражение читается: «возвести в куб число 6» или «6 в кубе».
Возвести в куб онлайн
Как возвести число в куб онлайн!? Введите нужное число, которое требуется возвести в куб и нажмите возвести в куб. Справа от равно появится число, которое возвели в куб
Ну и далее пробежимся по нескольким поисковым запросам, которые так или иначе вы задаете в строке поиска!
Дополнительная информация
Квадратом числа называют произведение двух одинаковых множителей.
Мы уже пробовали находить квадраты первого десятка натуральных чисел.
Возводить двузначные числа, трехзначные и т.д. числа немного сложнее, главное хорошо знать и помнить таблицу умножения чисел.
Существует способ быстрого возведения в квадрат двухзначных чисел, которые оканчиваются на цифру 5.
1) Первую цифру числа, возводимого в квадрат, необходимо умножить на сумму этого числа и единицы.
2) Записать полученное число- это будут первые цифры ответа (с этих цифр начинается ответ).
3) Ответ всегда будет заканчиваться на 25 (т.е. в конце ответа всегда будет стоять число 25).
4) Приписываем к числу, полученному в п 2, число 25, получаем ответ.
Рассмотрим поясняющий пример.
Найдем квадрат 65.
65 2 = 65 ∙ 65
Первая цифра в числе 6 5– это цифра 6 , следовательно, нам необходимо найти произведение 6 и суммы 6 + 1.
6 ∙ (6 + 1) = 6 ∙ 7 = 42
Запишем число 42 и припишем к нему число 25.
Проверим: Так как квадрат числа- это произведение двух одинаковых множителей 65 2 = 65 ∙ 65, то
65 2 = 65 ∙ 65 = 4225
Получили все тот же ответ: 65 2 = 4225
Источник
Решение №1633 Объём куба равен 24. Найдите объём треугольной призмы, отсекаемой от куба …
Объём куба равен 24. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Высота куба равна высоте треугольной призмы. Значит объём будет зависит от площади оснований. Рассмотрим основание треугольной призмы:
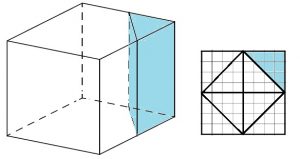
Основание куба состоит из 8 треугольников размером с основание призмы. Объём треугольной призмы будет в 8 раз меньше объёма куба:
Vтреуг. призмы = 24/8 = 3
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Источник