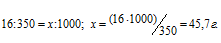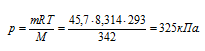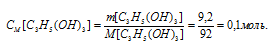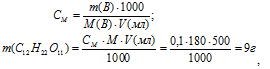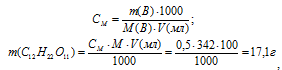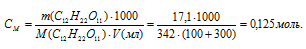Как найти осмотическое давление сахарозы

Задачи по химии на вычисление осмотического давления раствора

 Задача 463. 
Чему равно осмотическое давление 0,5 М раствора глюкозы С₆Н₁₂О₆ при 25°С?
Решение:
Согласно уравнению Р = С_МRT, где С_М – молярная концентрация, R – газовая постоянная [8,314 Д ж/(моль ^. К)], T – температура.
Рассчитаем осмотическое давление:

                           Р = 0,5 .8,314 ^. 298 = 1238,786 кПа = 1,24 МПа.

Ответ: 1,24 МПа.

Задача 464.
Вычислить осмотическое давление раствора, содержащего 16 г сахарозы С₁₂Н₂₂О₁₁ в 350 г Н₂О при 293 К. Плотность раствора считать равной единице.
Решение:
M(С₁₂Н₂₂О₁₁) = 342 г/моль. Для расчётов используем  уравнение  Р = С_МRT,  С_М – молярная концентрация, R – газовая постоянная [8,314 Дж/(моль ^. К)] , T – температура. С_М можно выразить через массу растворённого вещества (m) и его мольную массу (М). Массу сахара, содержащегося в 1000 мл раствора, найдём из пропорции:

Отсюда

Ответ: 325 кПа.

Задача 465.
Сколько граммов глюкозы С₆Н₁₂О₆ должно находиться в 0,5 л раствора, чтобы его осмотическое давление (при той же температуре) было таким же, как раствора, в 1 л которого содержится 9,2 г глицерина  С₃Н₅(ОН)₃?
Решение:
М(С₆Н₁₂О₆)  = 180г/моль, М[С₃Н₅(ОН)_3] = 92г/моль. Осмотическое давление определяется по формуле: Р = С_MRT, где С_М – молярная концентрация, R – газовая постоянная [8,314 Дж/(моль ^. К)] , T – температура. Из данного уравнения вытекает, что осмотическое давление растворов зависит от концентрации и температуры. 

Таким образом, осмотическое давление двух растворов будет одинаковым, если концентрации растворённых веществ будут одинаковыми при одной и той же температуре. Поэтому справедливо равенство:

Р(С₆Н₁₂О₆) = Р[С₃Н₅(ОН)₃];  С_М(С₆Н₁₂О₆)RT = С_М[С₃Н₅(ОН)₃]RT

Находим молярную концентрацию глицерина: 

Теперь рассчитаем, сколько граммов глюкозы содержится в 0,5 л 0,1М раствора по формуле:

где С_М, m(B), M(B) и V(мл) соответственно молярная концентрация, масса, молярная масса растворённого вещества и объём раствора. 

Ответ: 9 г.

Задача 466.
К 100 мл 0,5М водного раствора сахарозы   добавлено 300 мл воды. Чему равно осмотическое давление полученного раствора при 25°С?  
Решение:
M(С₁₂Н₂₂О₁₁) = 342 г/моль.
Для расчёта массы С₁₂Н₂₂О₁₁ используем формулу:

Рассчитаем молярную концентрацию полученного раствора сахарозы, находим:

Осмотическое давление полученного раствора находим из формулы:  P = C_MRT, где С_М – молярная концентрация, R – газовая постоянная [8,314 Дж/(моль ^. К)], Т – температура.

Тогда

P = 0,125 ^. 8,314 ^. 298 = 309,7 кПа.                      

Ответ: 309,7 кПа.

Для разб. р-ров электролитов ур-ние Вант-Гоффа имеет вид:

где i= 1 + a'(v Ч 1) (a’-степень диссоциации электролита, v-число ионов, на к-рые распадается молекула электролита). В случае сильных электролитов, полностью диссоциирующих на ионы, при высоких разбавлениях = 2RT,> для р-ра произвольной концентрации = vФ 2RT,> где Ф-практич. осмотич. коэффициент. Он непосредственно связан с коэф. активности растворенного в-ва и моляль-ностью m р-ра электролита соотношением Бьеррума:

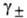
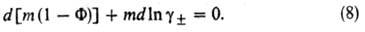
В интегральной форме соотношение (8) принимает вид:

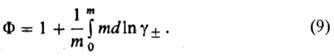
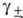
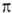
Это соотношение используют для расчета Ф по данным о ; можно рассчитать Ф и по значениям .

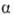
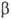
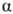
Наиб. существ. черта всех осмотич. процессов — увеличение объема р-ра. Оно всегда имеет место, если молекулы растворенного в-ва не могут выйти из р-ра, а р-ритель способен проникать в р-р. Это условие можно выполнить даже при отсутствии видимой полупроницаемой перегородки. Напр., если фазы и содержат нелетучий компонент и не разделены перегородкой, а находятся под одним колпаком, из-под к-рого откачан воздух, то за счет разности давлений насыщ. пара произойдет «перекачка» р-рителя из р-ра в р-р . Такой процесс получил назв. изотермич. перегонки. Др. примером типичного проявления О. без наличия полупроницаемой перегородки является набухание в системах полимер-р-ритель.

Осмос в природе. Животные и растит. клетки представляют собой микроскопич. осмотич. системы, поскольку у клетки оболочка или прилегающая к ней плазмолемма обладают св-вами полупроницаемых мембран. Если поместить клетки в дистиллированную воду, происходит набухание, а затем разрыв оболочек (осмотич. шок, или лизис). В р-рах с высокой концентрацией солей наблюдается падение осмотич. давления и коллапс клеток из-за потери воды (плазмолиз). Это явление используют, напр., при консервировании пищ. продуктов путем добавления больших кол-в соли или сахара: микроорганизмы подвергаются плазмолизу и становятся нежизнедеятельными.

Р-ры с одинаковым значением осмотич. давления наз. изотоническими. Р-ры с осмотич. давлением, большим, чем у внутриклеточной жидкости, наз. гипертоническими, меньшим-гипотоническими. Один и тот же р-р для одного типа клеток м. б. гипертоническим, для другого-изотоническим, для третьего-гипотоническим.

В тканях растений осмотич. давление составляет 0,5-2 МПа (у растений в пустынях — более 10 МПа). Гидро-статич. давление, возникшее во внутриклеточных структурах в результате осмоса, наз. тургором. Это давление придает прочность и упругость тканям живых организмов. Если клетка отмирает, оболочка теряет св-во полупроницаемости, тургор исчезает (растение вянет). Осмотич. давление-главная причина, обеспечивающая движение воды в растениях и ее подъем от корней до вершины. Клетки листьев, теряя воду, осмотически всасывают ее из клеток стебля, а последний-из клеток корня, берущих, в свою очередь, воду из почвы. Для роста и развития растений важно соотношение между осмотич. давлением почвенного р-ра и клеточного сока. Растение может нормально развиваться лишь тогда, когда осмотич. давление клеточного сока больше осмотич. давления почвенного р-ра.

Высокоорганизованные животные и человек отличаются постоянным значением осмотич. давления, напр. в крови человека 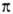= 0,78 МПа (7,7 атм) при 37 °С. Даже небольшие изменения осмотич. давления вызывают чувство дискомфорта. Так, чувство жажды обусловлено потребностью организма восстановить нормальное осмотич. давление введением воды, после того как оно было повышено, напр. употреблением соленой пищи. При болезненных явлениях локальные изменения осмотич. давления м. б. значительными. Напр., при воспалит. процессах происходит распад белков, что приводит к увеличению кол-ва структурных частиц в очаге воспаления, повышению осмотич. давления и локальному оттоку воды из окружающих тканей. Так возникают отеки.

В медицине обычно используют изотонич. р-ры, но иногда применяют и гипертонические. Так, в хирургии гипертонич. повязками покрывают раны: гипертонич. повязка оттягивает на себя жидкость и очищает рану от микроорганизмов, продуктов распада и т. д.

Лит.: Горшков В. И., Кузнецов И. А., Физическая химия, М., 1986; Дуров В. А., Агеев Е. П., Термодинамическая теория растворов неэлектролитов, М., 1987. См. также лит. при ст. Мембранные процессы разделения.

Е. П. Агеев.

After more than five years, it seems safe to assume that an explicit answer will no longer serve to furnish the OP with a homework solution, so I will post numerical values for all the steps already given in Curt F.’s answer:

Molality of the solution

The change in boiling temperature is $pu{1.45 K}$. Together with the boiling point elevation constant, we can calculate the molality of the solution as $pu{2.83 mol/kg}$.

Concentration of the solution

To figure out the concentration, let’s assume we have a solution containing $pu{1 kg}$ of solvent. So we would have $pu{2.83 mol}$ or $pu{0.9694 kg}$ of sucrose. We can get the mass of the solution as the sum of the mass of solvent and solute, and the volume of the solution because we also know the density. The concentration comes out as $pu{1.49 M}$. If you write down the calculation, you will see that the mass of solvent cancels out, giving you the following relationship between the molality $b$ and the concentration $c$:

$$c = frac{b cdot rho}{1 + M_mathrm{sucrose} cdot b}$$

with $M_mathrm{sucrose}$ the molar mass of sucrose and $rho$ the density of the solution at the relevant temperature. Density and concentration are temperature-dependent, while molality is not.

Osmotic pressure

The osmotic pressure comes out as $pu{37.6 atm}$ when you plug in the correct concentration, temperature and the universal gas constant into $Pi = c R T$.

Step-by-step math

$ΔT = 1.45 mathrm{K}$

$k_{mathrm{b}} = 0.512 frac{mathrm{K} mathrm{kg}}{mathrm{mol}}$

$b = dfrac{ΔT}{k_{mathrm{b}}}$

$ =dfrac{1.45 mathrm{K}}{0.512 frac{mathrm{K} mathrm{kg}}{mathrm{mol}}}$

$ =2.83 frac{mathrm{mol}}{mathrm{kg}}$

$ρ = 1.036 frac{mathrm{kg}}{mathrm{L}}$

$m_{mathrm{solvent}}$ $= 1 mathrm{kg}$

$c = dfrac{ρ}{dfrac{1}{b} + M_{mathrm{ce{C12H22O11}}}}$

$ =dfrac{1.036 frac{mathrm{kg}}{mathrm{L}}}{dfrac{1}{2.83 frac{mathrm{mol}}{mathrm{kg}}} + 342.30 frac{mathrm{g}}{mathrm{mol}}}$

$ =dfrac{1.036 frac{mathrm{kg}}{mathrm{L}}}{0.3531 frac{mathrm{kg}}{mathrm{mol}} + 342.30 frac{mathrm{g}}{mathrm{mol}}}$

$ =dfrac{1.036 frac{mathrm{kg}}{mathrm{L}}}{0.6954 frac{mathrm{kg}}{mathrm{mol}}}$

$ =1.490 frac{mathrm{mol}}{mathrm{L}}$

$R = 0.08205 frac{mathrm{atm} mathrm{L}}{mathrm{K} mathrm{mol}}$

$T = 35. mathrm{°aC}$

$Π = c cdot R cdot T$

$ =1.490 frac{mathrm{mol}}{mathrm{L}} cdot 0.08205 frac{mathrm{atm} mathrm{L}}{mathrm{K} mathrm{mol}} cdot 35. mathrm{°aC}$

$ =0.12224 frac{mathrm{atm}}{mathrm{K}} cdot 308. mathrm{K}$

$ =37.7 mathrm{atm}$

Δt = Ккр ∙ Сm → Сm=Δt/Ккр
Ккр(воды)=1,86°С∙кг/моль
Мольная доля сахарозы в растворе:
Сm= –0,41°С/1,86°С∙кг/моль=0,220 моль/кг
В 1 кг воды растворены 0,220 ∙ 342 = 75 г (0,075 кг) сахарозы, масса раствора 1,075 кг.
Объем раствора V=m (p-pa) ∙ ρ= 1,075 кг / 1,2 кг/л = 0,896 л
Молярная конц-я сахарозы:
См=0,220 моль / 0,896 л = 0,246 моль/л
Осмотическое давление раствора при 2°С (275К):
Росм (кПа) = См ∙ R ∙ T(К) = 0,17 ∙ 8,31 ∙ 275 = 562 кПа