Как найти ось в слове - AvtoShod.ru - решение различных проблем

Игры со словами. Палиндромы
Палиндромы (перевертыши) − это слова и предложения, которые читаются одинаково слева направо и справа налево.
Например:
НАГАН;
А РОЗА УПАЛА НА ЛАПУ АЗОРА;
Я НЕ МИЛ − И НЕ ЖЕНИЛИ МЕНЯ;
АРГЕНТИНА МАНИТ НЕГРА.
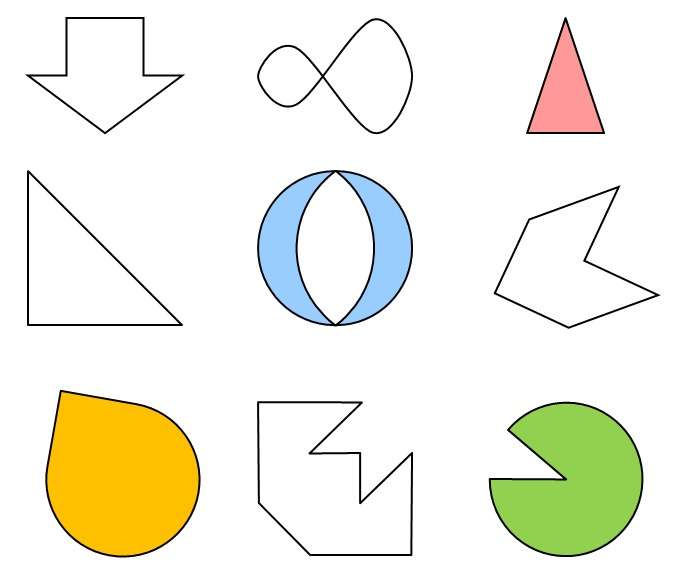
Среди слов, приведенных ниже, найди палиндромы, которые имеют оси симметрии:
ПОП, ДОВОД, ДОХОД, ПОТОП, ТОПОТ, ЗАКАЗ, КАЗАК.
Придумай свои палиндромы.

reshalka.com

ГДЗ учебник по математике 3 класс Петерсон. 17 урок. Симметричные фигуры. Номер №11

Решение

Слова ПОП, ДОХОД, ПОТОП и ТОПОТ имею оси симметрии.
Свои палиндромы:
И ЛЕЖУ. − УЖЕЛИ?
ЯД, ЯД, ДЯДЯ!
КИТ НА МОРЕ РОМАНТИК.
ДОВОД
КАБАК
КОМОК
РАДАР
ШАЛАШ

Источник

Суффиксы глаголов в русском языке

Суффиксы глаголов чаще всего имеют безударные гласные. Рассмотрим, как пишутся суффиксы глаголов в соответствии с правилами русского языка.

В морфемном составе глаголов суффиксы бывают словообразовательные и формообразующие. Словообразовательные суффиксы образуют глаголы совершенного и несовершенного вида. Узнаем, какое правило применить в написании безударных гласных в словообразовательных суффиксах.

Словообразовательные суффиксы глаголов

Суффиксы -ова-/ева-, -ыва-/-ива-

Суффиксы -ова-/-ева- и -ыва-/-ива- образуют глаголы несовершенного вида:

(что сделать?) осво́ить → (что делать?) осва́ ива ть;
(что сделать?) разма́зать → (что делать?) разма́з ыва ть.

Поставив ударение, убедимся, что гласные в глагольных суффиксах являются безударными, из-за чего возникает затруднение в их написании. Чтобы не ошибиться в выборе букв «о», «е» или «ы», «и» в суффиксах, применим правило орфографии.

Понаблюдаем, как применить это правило:

я распроб ую — распро́б о ва ть, распро́б о вал;
я облиц ую — облиц е ва́ ть, облиц е ва́л;
запазд ываю — запа́зд ыва ть, запа́зд ы вал;
подмеш иваю — подме́ш и ва ть, подме́ш и вал.

Слова с этимологическим корнем -вед- («знать») пишутся по-разному. Часть этих глаголов имеет суффикс -ова-:

завед ую — завед ова ть, заведовал;
исповед ую — исповед ова ть, исповедовал;
проповед ую — проповед ова ть, проповедовал.

А другая часть глаголов сохраняет суффикс -ыва- во всех грамматических формах:

провед ыва ю — провед ыва ть, провед ыва л;
вывед ыва ю — вывед ыва ть, вывед ыва л;
отвед ыва ю — отвед ыва ть, отвед ыва л;
развед ыва ю — развед ыва ть, развед ыва л.

Суффикс -ва-

Отличаем эти глаголы от слов с ударным суффиксом -ва-:

разбить → раз б и ва́ ть;
созреть → со зр е ва́ ть.

Гласный корня, обозначенный буквами «е», «и», оказался в безударной позиции. Чтобы правильно написать такое слово, воспользуемся правилом орфографии.

Примеры

узна́ть → узн а в а́ ть;
запе́ть → зап е ва́ ть;
проли́ть → прол и ва́ ть;
запи́ть → зап и ва́ ть.

Исключения:

застр я́ ть — застр е ва́ть;
затм и́ ть — затм е ва́ть;
растл и́ ть — растл е ва́ть;
продл и́ ть — продл е ва́ть.

Буквы «е», «ё», «и» в суффиксах глаголов

1. В суффиксах глаголов после шипящих основы пишутся буквы «е», «ё»:

затуш е ва́ ть → затуш ё вы вать;
корч е ва́ ть → раскорч е ва ть → раскорч ёв ыва ть;
ночь → ноч е ва́ть;
межа → меж е ва́ть → размеж е ва́ть → размежёвывать;
увещ е ва́ть.

2. В безударных суффиксах пишутся буквы «и» или «е» у глаголов с приставками о-бес/о-без-. Этот выбор сделаем в зависимости от категории переходности глагола и от смысла слова в контексте.

Переходные глаголы пишутся с суффиксом -и-, а непереходные — с суффиксом -е-.

Сравним:

Наша земля совсем обесплод е ла.

Она обессил е ла от этой тяжелой ноши.

Формообразующие суффиксы глаголов

Суффикс -л-

Формы прошедшего времени изъявительного наклонения и условного наклонения глаголов образует суффикс -л-, который присоединяется к основе неопределенной формы:

написа ть — написа л письмо, написа л бы картину;
узна ть — узна л новость; узна л бы поточнее.

вы́смотр е ть — высмотр е л;
перекра́с и ть — перекра́с и л;
та́ я ть — та́ я ла;
му́ч и ть — му́ч и л.

Чтобы правильно написать безударный суффикс, обозначенный буквой -я- перед формообразующим суффиксом -л-, запомним список глаголов:

веять, затеять, каяться, лаять, лелеять, маяться;
надеяться, отчаяться, реять, сеять, таять, хаять, чуять.

Нулевой суффикс

Суффикс -л- может быть материально не выраженным буквами или звуками. Наличие нулевого суффикса в форме единственного числа мужского рода можно определить, если сравнить с другими формами прошедшего времени, в которых он проявляет себя.

Сравним:

ползти — он полз , гусеница полз л а, насекомое полз л о;
высохнуть — ствол высох , лужа высох л а, поле высох л о.

Формообразующие морфемы повелительного наклонения

С помощью формообразующего суффикса -и- или нулевого суффикса образуются формы единственного числа повелительного наклонения глаголов. Постфикс -те участвует в грамматическом оформлении глаголов множественного числа:

нести — нес и , нес и те ;
тащить — тащ и , тащ и те ;
навьючить — навьючь , навьючь те ;
резать — режь , режь те .

Постфикс -ся (-сь)

С помощью постфикса -ся(-сь) образуются возвратные глаголы:

купать — купать ся ;
нести — нести сь .

Морфема -ся пишется после согласных, а -сь после гласных основы.

Таблица

Суффикс	Условия	Примеры
-ова- (-ева-)	В неопределенной форме и в форме прошедшего времени, если глагол в 1-м лице ед. числа настоящего времени оканчивается на -ую, -юю.	ноч ева ть (ноч ую ) бесед ова ть (бесед ую ) гор ева ть (гор юю )
-ыва- (-ива-)	В неопределенной форме и в форме прошедшего времени, если глагол в 1-м лице ед. числа настоящего времени оканчивается на -ываю, -иваю.	рассказ ыва ть (рассказ ываю ) учит ыва ть (учит ываю ) наста ива ть (наста иваю )
-л	В основе глагола прошедшего времени перед суффиксом -л пишется та же гласная, что и перед -ть в неопределенной форме.	нач а л (нач а ть) пон я л (пон я ть) кле и л (кле и ть) ве я л (ве я ть) вид е л (вид е ть)

Правописание суффиксов глаголов