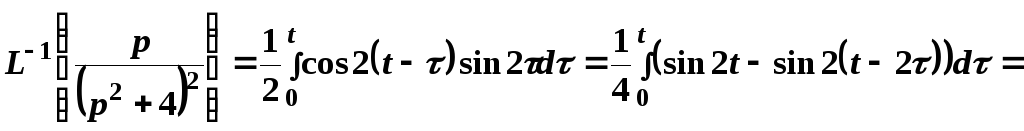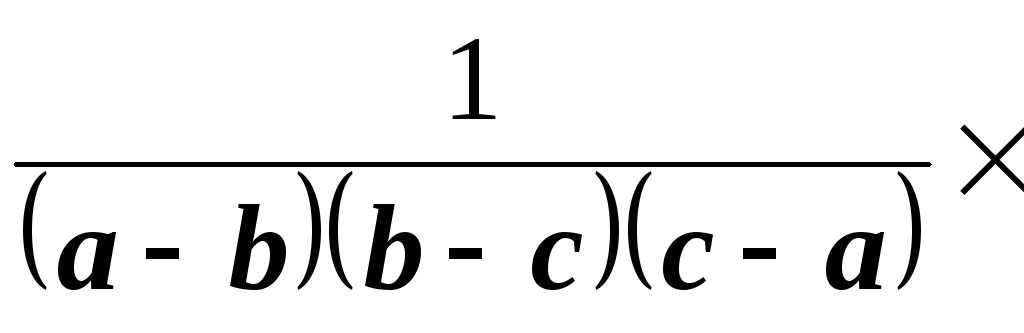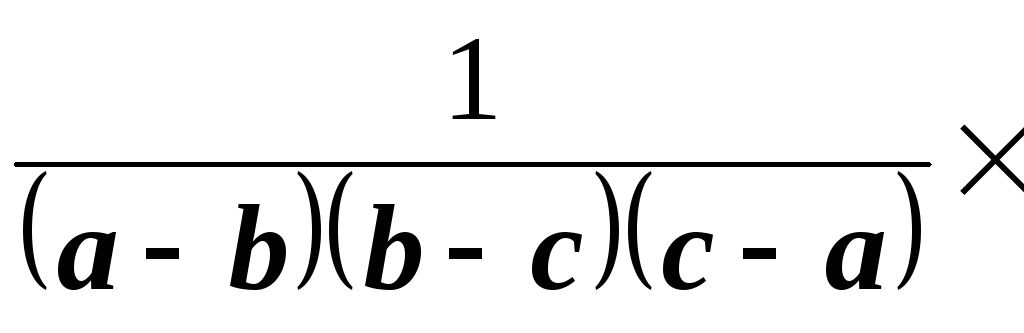Обратное преобразования Лапласа онлайн, калькулятор для оригиналов функций по изображению.
Теория функций комплексного переменного.
: x^a
модуль x: abs(x)
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
 : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]
Преобразованием Лапласа некоторой функции
называется интегральное преобразование вида:
Функция
называется оригиналом, функция
— изображением. Причём
является функцией комлексной переменной, т.е.
.
В качестве примера, найдём изображение
функции оригинала
.
Для этого нам необходимо воспользоваться приведённой выше формулой и
вычислить интеграл:
То, что функция
является изображением функции
записывается как
или
.
Важным свойством
преобразования Лапласа
является то, что если
, то
Указанное свойство активно используется при
решении дифференциальных уравнений
поскольку позволяет сводить последние к алгебраическим.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет найти преобразование Лапласа практически любой, даже очень сложной функции.
|
19:26 найти оригинал функции по ее изображению |
|
Калькулятор для оригиналов функций по изображению (калькулятор обратного преобразования Лапласа ) |
Категория: Теория функций комплексного переменного | Просмотров: 34918 | Добавил: Admin | Теги: тфкп | Рейтинг: 4.5/2 |
Как найти похожую картинку, фотографию, изображение в интернет
12.07.2019
Допустим у Вас есть какое-то изображение (рисунок, картинка, фотография), и Вы хотите найти такое же (дубликат) или похожее в интернет. Это можно сделать при помощи специальных инструментов поисковиков Google и Яндекс, сервиса TinEye, а также потрясающего браузерного расширения PhotoTracker Lite, который объединяет все эти способы. Рассмотрим каждый из них.
Поиск по фото в Гугл
Тут всё очень просто. Переходим по ссылке https://www.google.ru/imghp и кликаем по иконке фотоаппарата:
Дальше выбираем один из вариантов поиска:
- Указываем ссылку на изображение в интернете
- Загружаем файл с компьютера
На открывшейся страничке кликаем по ссылке «Все размеры»:
В итоге получаем полный список похожих картинок по изображению, которое было выбрано в качестве образца:
Есть еще один хороший способ, работающий в браузере Chrome. Находясь на страничке с интересующей Вас картинкой, подведите к ней курсор мыши, кликните правой клавишей и в открывшейся подсказке выберите пункт «Найти картинку (Google)»:
Вы сразу переместитесь на страницу с результатами поиска!
Статья по теме: Поисковые сервисы Google, о которых Вы не знали!
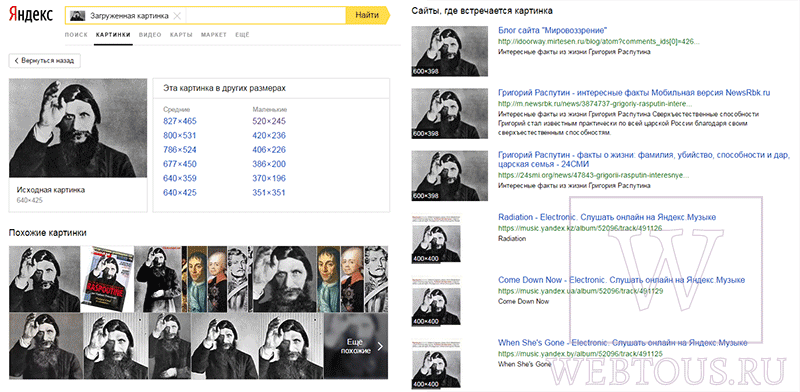
Поиск по картинкам в Яндекс
У Яндекса всё не менее просто чем у Гугла 
Укажите адрес картинки в сети интернет либо загрузите её с компьютера (можно простым перетаскиванием в специальную области в верхней части окна браузера):
Результат поиска выглядит таким образом:
Вы мгновенно получаете доступ к следующей информации:
- Какие в сети есть размеры изображения, которое Вы загрузили в качестве образца для поиска
- Список сайтов, на которых оно встречается
- Похожие картинки (модифицированы на основе исходной либо по которым алгоритм принял решение об их смысловом сходстве)
Поиск похожих картинок в тинай
Многие наверняка уже слышали об онлайн сервисе TinEye, который русскоязычные пользователи часто называют Тинай. Он разработан экспертами в сфере машинного обучения и распознавания объектов. Как следствие всего этого, тинай отлично подходит не только для поиска похожих картинок и фотографий, но их составляющих.
Проиндексированная база изображений TinEye составляет более 10 миллиардов позиций, и является крупнейших во всем Интернет. «Здесь найдется всё» — это фраза как нельзя лучше характеризует сервис.
Переходите по ссылке https://www.tineye.com/, и, как и в случае Яндекс и Google, загрузите файл-образец для поиска либо ссылку на него в интернет.
На открывшейся страничке Вы получите точные данные о том, сколько раз картинка встречается в интернет, и ссылки на странички, где она была найдена.
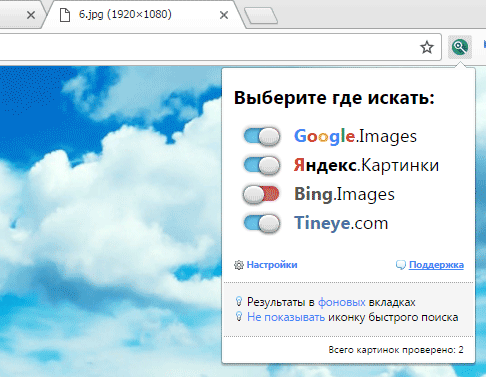
PhotoTracker Lite – поиск 4в1
Расширение для браузера PhotoTracker Lite (работает в Google Chrome, Opera с версии 36, Яндекс.Браузере, Vivaldi) позволяет в один клик искать похожие фото не только в указанных выше источниках, но и по базе поисковика Bing (Bing Images)!
Скриншот интерфейса расширения:
В настройках приложения укажите источники поиска, после чего кликайте правой кнопкой мыши на любое изображение в браузере и выбирайте опцию «Искать это изображение» PhotoTracker Lite:
Есть еще один способ поиска в один клик. По умолчанию в настройках приложения активирован пункт «Показывать иконку быстрого поиска». Когда Вы наводите на какое-то фото или картинку, всплывает круглая зеленая иконка, нажатие на которую запускает поиск похожих изображений – в новых вкладках автоматически откроются результаты поиска по Гугл, Яндекс, Тинай и Бинг.
Расширение создано нашим соотечественником, который по роду увлечений тесно связан с фотографией. Первоначально он создал этот инструмент, чтобы быстро находить свои фото на чужих сайтах.
Когда это может понадобиться
- Вы являетесь фотографом, выкладываете свои фото в интернет и хотите посмотреть на каких сайтах они используются и где возможно нарушаются Ваши авторские права.
- Вы являетесь блогером или копирайтером, пишите статьи и хотите подобрать к своему материалу «незаезженное» изображение.
- А вдруг кто-то использует Ваше фото из профиля Вконтакте или Фейсбук в качестве аватарки на форуме или фальшивой учетной записи в какой-либо социальной сети? А ведь такое более чем возможно!
- Вы нашли фотографию знакомого актера и хотите вспомнить как его зовут.
На самом деле, случаев, когда может пригодиться поиск по фотографии, огромное множество. Можно еще привести и такой пример…
Как найти оригинал заданного изображения
Например, у Вас есть какая-то фотография, возможно кадрированная, пожатая, либо отфотошопленная, а Вы хотите найти её оригинал, или вариант в лучшем качестве. Как это сделать? Проводите поиск в Яндекс и Гугл, как описано выше, либо средствами PhotoTracker Lite и получаете список всех найденных изображений. Далее руководствуетесь следующим:
- Оригинальное изображение, как правило имеет больший размер и лучшее качество по сравнению с измененной копией, полученной в результате кадрирования. Конечно можно в фотошопе выставить картинке любой размер, но при его увеличении относительно оригинала, всегда будут наблюдаться артефакты. Их можно легко заметить даже при беглом визуальном осмотре.
Статья в тему: Как изменить размер картинки без потери в качестве.
- Оригинальные фотографии часто имеют водяные знаки, обозначающие авторство снимка (фамилия, адрес сайта, название компании и пр.). Конечно водяной знак может добавить кто угодно на абсолютно на любое изображение, но в этом случае можно поискать образец фото на сайте или по фамилии автора, наверняка он где-то выкладывает своё портфолио онлайн.
- И наконец, совсем простой признак. Если Ваш образец фото черно-белый (сепия и пр.), а Вы нашли такую же, но полноцветную фотографию, то у Вас явно не оригинал. Добавить цветность ч/б фотографии гораздо более сложнее, чем перевести цветную фотографию в черно-белую
Уважаемые читатели, порекомендуйте данный материал своим друзьям в социальных сетях, а также задавайте свои вопросы в комментариях и делитесь своим мнением!
Похожие публикации:
- Как включить новый дизайн Фейсбук и темную тему
- Какие программы можно без опасений удалить с компьютера?
- Как заряжать смартфон быстрее – 7 полезных советов
- Что о Вас знает Яндекс и как удалить свои персональные данные?
- TFW – что это значит и когда употребляется
Понравилось? Поделитесь с друзьями!
Сергей Сандаков, 42 года.
С 2011 г. пишу обзоры полезных онлайн сервисов и сайтов, программ для ПК.
Интересуюсь всем, что происходит в Интернет, и с удовольствием рассказываю об этом своим читателям.
Рассмотрим
простейшие приемы нахождения оригинала
по известному изображению. Один из них
основан на использовании таблицы
изображений, которая в этом случае
рассматривается в обратном порядке, и
правил операционного исчисления. В
первую очередь это относится к теореме
смещения, интегрированию и дифференцированию
изображения и изображению свертки
функций.
Пример
12.
Найти оригинал f(t),
если
.
Решение.
Исходным можно взять соответствие
.
Операции
смещения на а
в области изображений соответствует
операция домножения на
в области оригиналов. Поэтому при а=1
имеем
.
Операции
домножения на
в области изображений соответствует
запаздывание на =2
в области оригиналов. Следовательно,
Пример
13.
Найти оригинал изображения
.
Решение.
Выделим в знаменателе полный квадрат
.
Воспользуемся
равенством
,
а также теоремой смещения. В результате
получим
.
Пример
14.
Найти оригинал, соответствующий
изображению
.
Решение.
Можно поступить так: за исходное взять
соотношение
.
Затем
воспользуемся тем, что делению на р
в области изображений соответствует
операция интегрирования в области
оригиналов:

Это же свойство
применим повторно:
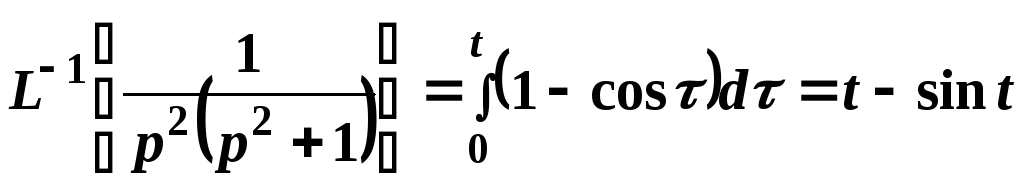
Заметим,
что оригинал указанного изображения
проще можно было бы найти, если разложить
его на простейшие дроби:
.
Согласно
свойству линейности имеем
.
Пример
15.
Найти оригинал изображения
.
Решение.
Представим изображение в виде
.
Произведению
изображений
и
соответствует свертка их оригиналов
и
.
Поэтому
.
Для
этого изображения оригинал можно найти
проще, если воспользоваться тем, что
операции дифференцирования в области
изображений соответствует операция
домножения на (-t)
в области оригиналов. Поэтому

Очень
часто при решении практических задач
возникает необходимость нахождения
оригиналов изображений, которые
представляются в виде дробно рациональной
функции
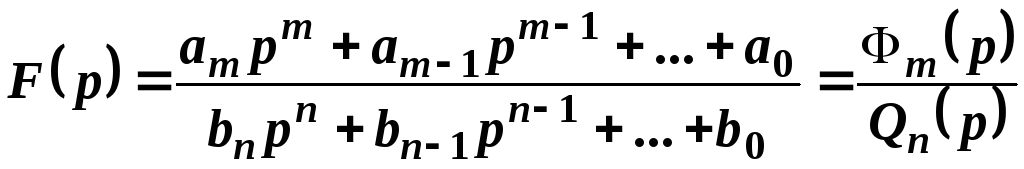
в
которой старшая степень числителя
меньше старшей степени знаменателя
переменной р.
При
нахождении оригинала такой дроби
разлагают ее на сумму простых дробей с
помощью метода неопределенных
коэффициентов, известного из интегрального
исчисления. Затем находят оригиналы
для каждой простой дроби.
Пример
16.
Найти оригинал, соответствующий
изображению
.
Решение.
Разложим данную дробь на сумму простейших
дробей. Для этого, прежде всего, найдем
корни знаменателя, решив уравнение
.
Проверкой убеждаемся, что
один из его корней. Разделим кубический
многочлен
на двучлен р+1.
В частном получим
.
Дискриминант этого трехчлена —
отрицательный, на действительные
множители он не разлагается. Разложение
данного изображения на простейшие дроби
имеет вид:
.
Отсюда
.
Полагая
в этом равенстве
,
находим
.
Затем приравниваем коэффициенты при
одинаковых степенях р:
,
.
Таким
образом,
.
В
знаменателе второй дроби выделим полный
квадрат, а в числителе — двучлен
:
.
Используя
свойство линейности , переходим в область
оригиналов. Получим
.
Заметим,
что в данном случае, прежде чем приступать
к разложению изображения на простейшие
дроби, было бы полезно воспользоваться
теоремой смещения. Для этого в исходном
изображении выделим двучлен
:
.
Тогда
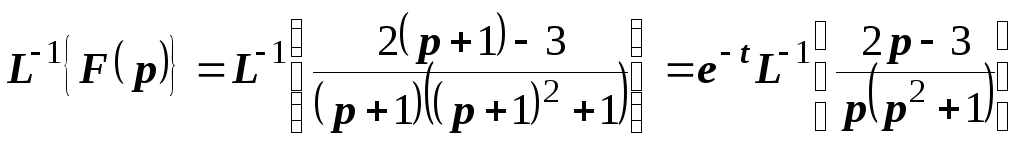
Разложение
полученного изображения на простейшие
дроби проще, чем исходного:
;
;
;
.
Оригиналом
будет функция
или
.
Задача
нахождения оригиналов, соответствующих
дробно-рациональным изображениям
упрощается, если воспользоваться
следующей краткой таблицей (табл. 3).
Таблица 3 –
Изображение – оригинал
|
№ |
Изображение |
Оригинал |
|||
|
1 |
2 |
3 |
|||
|
1 |
|
|
|||
|
2 |
|
|
|||
|
3 |
|
|
|||
|
4 |
|
|
|||
|
5 |
|
|
|||
|
6 |
|
|
|||
|
7 |
|
|
|||
|
8 |
|
|
|||
|
9 |
|
|
|||
|
1
0 |
|
|
Продолжение табл.
3
|
1 |
2 |
3 |
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


 : x^a
: x^a : Sqrt[x]
: Sqrt[x]![sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x]