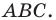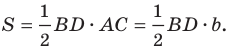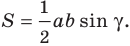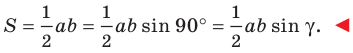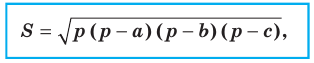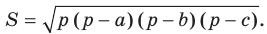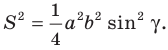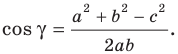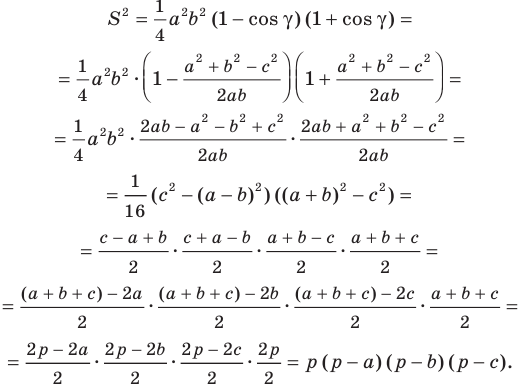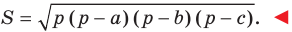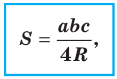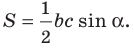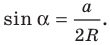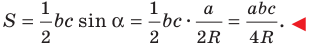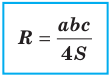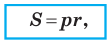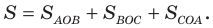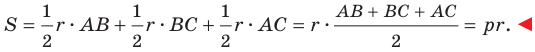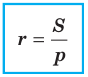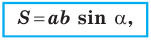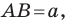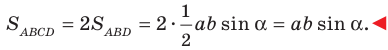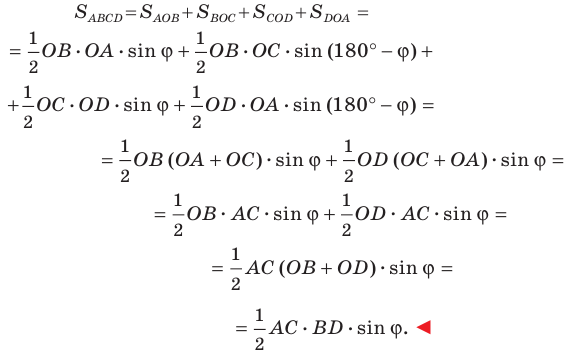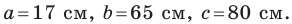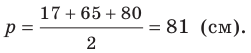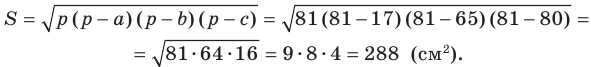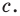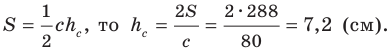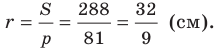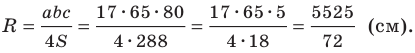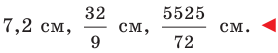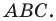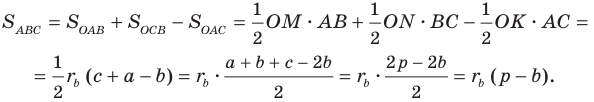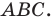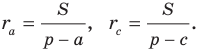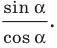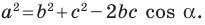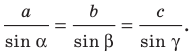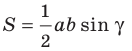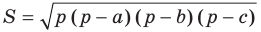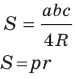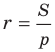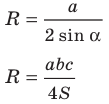Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Прямоугольная система координат на плоскости и ее применение с примерами
Содержание:
Прямоугольная система координат на плоскости и ее применение к простейшим задачам
Прямоугольные координаты точки на плоскости
Координатами точки на плоскости называются числа, определяющие положение этой точки на плоскости.
Прямоугольные декартовы координаты (по имени математика Декарта) на плоскости вводятся следующим образом: на этой плоскости выбираются точка О (начало координат) и проходящие через нее взаимно перпендикулярные направленные прямые Ох и Оу (оси координат) (рис. 1). Для удобства рассмотрения будем предполагать, что ось Ох 0ось абсцисс) горизонтальна и направлена слева направо, а ось Оу (ось ординат) вертикальна и направлена снизу вверх; таким образом, ось О у повернута относительно оси Ох на угол 90° против хода часовой стрелки 1 ). Кроме того, выбирается единица масштаба для измерения расстояний.
Для данной точки М введем в рассмотрение два числа: абсциссу х и ординату у этой точки.
Абсциссой х называется число, выражающее в некотором масштабе расстояние от точки до оси ординат, взятое со знаком плюс, если точка лежит вправо от оси ординат, и со знаком минус, если точка лежит влево от оси ординат. Ординатой у называется число, выражающее в некотором масштабе (обыкновенно в том же, как и для абсциссы) расстояние от точки до оси абсцисс, взятое со знаком плюс, если точка лежит выше оси абсцисс, и со знаком минус, если точка лежит ниже оси абсцисс.
Эти два числа х и у и принимаются за координаты точки М, так как они полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка, координатами которой являются эти числа; и обратно, каждая точка плоскости имеет определенные координаты х и у. Если точка М имеет координаты х и у, то это обстоятельство обозначают так: М (х, у) (на первом месте ставится абсцисса х, а на втором — ордината у). При записи координат знак плюс, как обычно, можно опускать.
Оси Ох и Оу разбивают плоскость на четыре части, называемые квадрантами. Производя нумерацию квадрантов (I, II, III и IV) в направлении против хода часовой стрелки, отправляясь от того квадранта, где обе координаты положительны, получим следующую таблицу знаков координат:
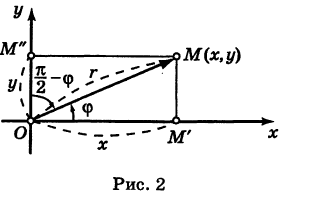
Отрезок ОМ у соединяющий начало координат О с точкой М (рис. 2), называется ее радиусом-вектором. Обозначая через ф угол, образованный отрезком ОМ с положительным направлением оси Ох, и через 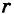
Нетрудно убедиться, что формулы (1) будут справедливы для координат точек всех квадрантов. Таким образом, знак абсциссы х точки М совпадает со знаком косинуса, а знак ее ординаты у — со знаком синуса в соответствующем квадранте.
Легко видеть, что если точка лежит на оси абсцисс, то ее ордината у равна нулю; если же она лежит на оси ординат, ее абсцисса х равна нулю, и обратно. Следовательно, если точка совпадает с началом координат, то равны нулю обе ее координаты.
В дальнейшем прямоугольные декартовы координаты для краткости будем называть просто прямоугольными координатами.
В следующих параграфах рассмотрим некоторые простейшие задачи на применение прямоугольных координат на плоскости.
Преобразование прямоугольной системы координат
При решении задач иногда выгодно вместо данной прямоугольной системы координат 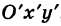
Возникает вопрос о том, как от одной системы координат перейти к другой.
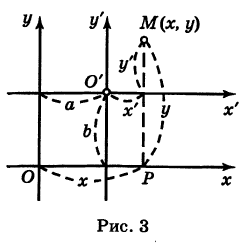
Рассмотрим сначала простейший случай (рис. 3), когда оси «новой системы координат» О’х’у’ параллельны соответствующим осям «старой системы координат о Оху и имеют одинаковые направления с ними (параллельный перенос системы координат).
Пусть начало новой системы координат — точка О’ — имеет координаты (а, Ь) в старой системе координат. Точка М плоскости со «старыми координатами» (х, у) будет иметь некоторые «новые координаты» [х у’] (для ясности мы их обозначаем квадратными скобками). Из рис. 3 непосредственно получаем
х’ = х — а, у’ = у — b, (1)
т. е. новые координаты точки равны ее старым координатам минус старые координаты нового начала.
Обратно, из (1) находим
х = х’ + а, у = у’ + Ь. (2)
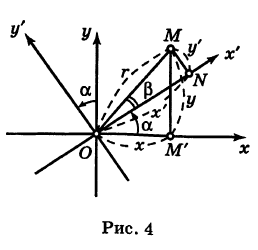
Пусть теперь «новая система» координат Ох’у при неизменном начале О, повернута относительно «старой системы» Оху на угол а (рис. 4), т. е. 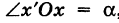
Обозначим через 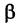
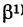
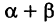
Так как новые координаты точки М, очевидно, есть
то из формул (3) и (4) получаем
Для запоминания формул (6) используют следующий мнемонический прием: говорят, что первая формула (6) содержит полный беспорядок, а вторая — полный порядок. Действительно, в первой формуле на первом месте стоит cos, на втором — sin; кроме того, присутствует знак минус. Во второй формуле (6) никаких нарушений правильности в этом смысле нет.
Формулы (6) выражают старые координаты х и у точки М через ее новые х’ и у’. Чтобы выразить новые координаты х’ и у’ через старые х и у, достаточно разрешить систему (6) относительно х’и у’. Однако можно поступить проще, а именно принять систему Ох’у’ за «старую», а систему Оху за «новую». Тогда, учитывая, что вторая система повернута относительно первой на угол — а, заменяя в формулах (6) х’ и у’ соответственно на х и у и обратно и принимая во внимание, что cos (-a) = cos a, sin (-a) = -sin a, будем иметь
Наконец, в общем случае, когда новое начало координат есть точка О’ (a, Ь) и ось О’х’ образует с осью Ох угол а, соединяя формулы (2) и (6), находим
Здесь угол Р считается положительным, если радиус-вектор ОМ повернут относительно оси Ох’ против хода часовой стрелки, и отрицательным, если он повернут относительно этой оси по ходу часовой стрелки.
Аналогично, из формул (1) и (7) получаем
Из формул (8) и (9) вытекает, что формулы перехода от одной прямоугольной системы координат к другой прямоугольной системе координат являются линейными функциями как новых, так и старых координат, т. е. содержат эти координаты в первой степени.
Пример:
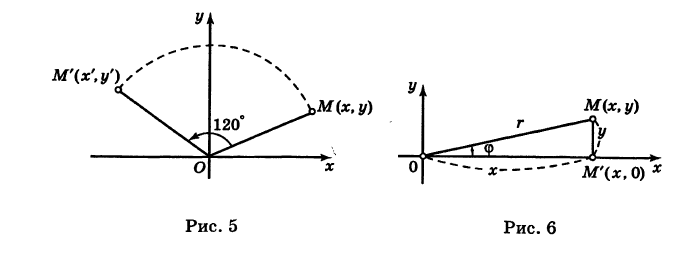
Отрезок ОМ, где точка М имеет координаты (х, г/), повернут на угол а = 120° против хода часовой стрелки (рис. 5). Каковы будут координаты х’ и у’ нового положения М’ точки М?
Решение:
Предполагая, что с точкой М связана подвижная система координат Ох’у на основании формул (6) будем иметь
Расстояние между двумя точками на плоскости
1) Найдем сначала расстояние г от начала координат О (0, 0) до точки М (х, у) (рис. 6).
Расстояние г = ОМ, очевидно, является гипотенузой прямоугольного 
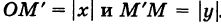
Таким образом, расстояние от начала координат до некоторой точки равно корню квадратному из суммы квадратов координат этой точки.
2) В общем случае, пусть для точек A 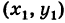
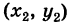
Выберем новую систему координат Ах’у’ начало которой совпадает с точкой А и оси которой параллельны прежним осям и имеют, соответственно, одинаковые направления с ними. Тогда в новой системе координат точки Л и В будут иметь координаты А [0, 0] и Б 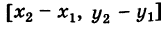
т. е. расстояние между двумя точками плоскости (при любом их расположении) равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.
Замечание. Формула (2) дает также длину отрезка АВ. Легко определить направление этого отрезка. Из прямоугольного А ABC имеем
(dx и dy называются проекциями отрезка АВ на оси координат Оху). Отсюда получаем 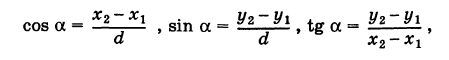
Пример:
Танк на местности переместился из точки А (-30, 80) в точку Б (50, 20) (относительно некоторой системы координат Оху)> причем координаты точек даны в километрах. Найти путь d, пройденный танком, если он двигался, не меняя направления.
Решение:
Применяя формулу (2), имеем
Деление отрезка в данном отношении
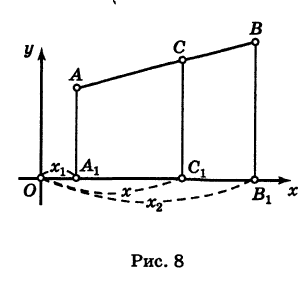
Предположим, что отрезок АВ (рис. 8), соединяющий точки A (xl9 уг) и В (x2t у2), разделен точкой С на два отрезка АС и СБ, причем отношение АС к СБ равно I (I > 0):
Требуется выразить координаты х и у точки С(х, у) через координаты концов отрезка АВ.
Опустим перпендикуляры 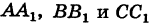
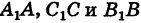
откуда на основании равенства (1) будем иметь
Из рис. 8 видно, что 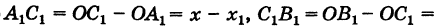
Решая уравнение (3) относительно неизвестной абсциссы х, будем иметь
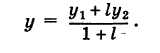
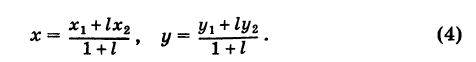
т. е. координаты середины отрезка равны полусуммам соответствующих координат его концов.
Примечание. При выводе формул (4) и (5) мы предполагали, что концы А и В отрезка АВ лежат в первом квадранте и, следовательно, координаты точек Аи В положительны. Легко доказать, что формулы (4) и (5) будут справедливы и в случае произвольного расположения отрезка АВ на координатной плоскости.
Пример:
Вычислить координаты точки С (х, у)> делящей отрезок АВ между точками А (-5, -3) и В (4, -6) в отношении АС/СВ = 3/2.
Решение:
В этом случае I = 3/2 и, следовательно,
Площадь треугольника
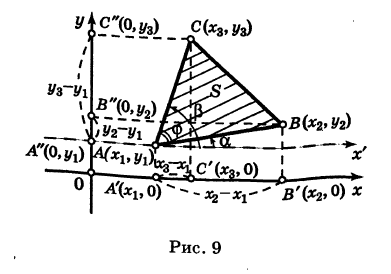
Пусть требуется найти площадь S треугольника ABC (рис. 9) с вершинами
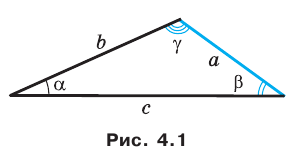
Пусть АВ = с, АС = Ь, а углы, образованные этими сторонами с осью Ох, соответственно равны 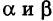
На основании (см. замечание) имеем (рис. 9)
и
Пусть 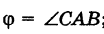
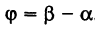
Отсюда в силу (1) и (2) имеем
Заметим, что формула (4) при ином расположении вершин может дать площадь треугольника S со знаком минус. Поэтому формулу для площади треугольника обычно пишут в виде
где знак выбирается так, чтобы для площади получалось положительное число,
Используя понятие определителя второго порядка
формулу (4′) можно записать в удобной для запоминания форме:
Формула (4′) упрощается, если точка А 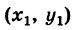
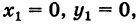
Отметим, что если точки А, В, С находятся на одной прямой, то площадь S = 0; и обратно, если S = 0, то вершины А, Б и С расположены на одной прямой.
Пример:
Вспаханное поле имеет форму треугольника с вершинами А (-2, -1), В (3, 5) и С (-1, 4) (размеры даны в километрах). Определить площадь S этого поля.
По формуле (5) имеем
Замечание. Вычисление площади многоугольника сводится к вычислению площадей треугольников. Для этого достаточно разбить многоугольник на треугольники, площади которых вычисляют по формуле (4).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
- Уравнения поверхности и линии в пространстве
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Задача 22142 1. Площадь треугольника ABC с вершинами.
Условие
1. Площадь треугольника ABC с вершинами А(-2; 1), В(2; 2), C(4; y) равна 15. Найти ординату вершины С.
Решение
Площадь треугольника равна половине модуля векторного произведения векторов СА и СB.
S (Δ ABC) =(1/2)*|vector×vector|
S (Δ ABC) = 1/2 * |4y-10|
S(Δ ABC) = |2у-5|.
По условию S(Δ ABC) =15,
получаем уравнение
|2у-5|=15.
2y-5=-15 или 2у-5=15
у=-5 или у=10
http://www.evkova.org/pryamougolnaya-sistema-koordinat-na-ploskosti
http://reshimvse.com/zadacha.php?id=22142
Таблица 1
| 1. Определение тригонометрических функций | ||
| Через единичную окружность (R = 1) |
Через произвольную окружность (R — радиус окружности) |
Через прямоугольный треугольник (для острых углов) |
|
sin α = y — tg α = y/x = sin α / cos α ctg α = x/y = cos α / sin α |
sin α = y / R cos α = x / R tg α = y / x ctg α = x / y |
sin α = a / c cos α = b / c tg α = a / b ctg α = b / a |
| 2. Тригонометрические функции числового аргумента | ||
|
sin (числа α) = sin (угла в α радиан) cos (числа α) = cos (угла в α радиан) tg (числа α) = tg (угла в α радиан) ctg (числа α) = ctg (угла в α радиан) |
||
| 3. Линии тангенсов и котангенсов |
|
tg α = yA — |
СВ — линия котангенсов (СВ || Oх) |
Объяснение и обоснование
1. Определение тригонометрических функций. Из курса геометрии вам известно определение тригонометрических функций острого угла в прямоугольном треугольнике. Напомним их.
Синусом острого угла α в прямоугольном треугольнике называется отношение длины противолежащего катета к длине гипотенузы: sin α = a / c (рис. 61).
Косинусом острого угла α в прямоугольном треугольнике называется отношение длины прилежащего катета к длине гипотенузы: cos α = b / c.
Тангенсом острого угла α в прямоугольном треугольнике называется отношение длины противолежащего катета к длине прилежащего: tg α = a / b.
Котангенсом острого угла α в прямоугольном треугольнике называется отношение длины прилежащего катета к длине противолежащего: ctg α = b / a.
В курсе геометрии было обосновано, что синус и косинус острого угла зависят только от величины угла и не зависят от длин сторон треугольника и его расположения, то есть синус и косинус (а таким образом, и тангенс, и котангенс) являются функциями величины угла, которые называются тригонометрическими функциями.
Для сокращения формулировок мы будем использовать термин «тригонометрическая функция угла», понимая, что рассматривается «тригонометрическая функция величины угла» (при этом величина угла может быть выражена как в радианах, так и в градусах).
Рис. 61
Также в курсе геометрии с использованием окружности с центром в начале координат было введено определение тригонометрических функций для углов от 0° до 180°. Эти определения можно применить для нахождения тригонометрических функций любых углов. Напомним их (но теперь будем рассматривать любые углы α от –∞ до +∞).
Возьмем окружность радиуса R с центром в начале координат. Обозначим точку окружности на положительной полуоси абсцисс через P0 (рис. 62). Необходимые нам углы будем образовывать поворотом радиуса OP0 около точки O. Пусть в результате поворота на угол α около точки O радиус OP0 займет положение OPα (говорят, что при повороте на угол α радиус OP0 переходит в радиус OPα, а точка P0 переходит в точку Pα). Напомним, что при α > 0 радиус OP0 поворачивается против часовой стрелки, а при α < 0 — по часовой стрелке.
Пусть точка Pα имеет координаты (x; y). Тогда:
синусом угла α называется отношение ординаты точки Pα (x; y) окружности к ее радиусу: sin α = y / R;
косинусом угла α называется отношение абсциссы точки Pα (x; y) окружности к ее радиусу: cos α = x / R;
тангенсом угла α называется отношение ординаты точки Pα (x; y) окружности к ее абсциссе: tg α = y / x (конечно, при x ≠ 0);
котангенсом угла α называется отношение абсциссы точки Pα (x; y) окружности к ее ординате: ctg α = x / y (при y ≠ 0).
Как и для тригонометрических функций острых углов, значения sin α, cos α, tg α, ctg α зависят только от величины угла α и не зависят от радиуса R*. Удобно взять R = 1, что позволит несколько упростить приведенные определения тригонометрических функций.
* Это следует из того, что две концентрические окружности гомотетичны (центр гомотетии — точка О, а коэффициент гомотетии k — отношение радиусов этих окружностей), тогда и точки Pα на этих окружностях также будут гомотетичны. Таким образом, при переходе от одной окружности к другой в определениях тригонометрических функций числитель и знаменатель соответствующей дроби умножаются на k, а значение дроби не изменяется.
Окружность радиуса 1 с центром в начале координат будем называть единичной окружностью.
Пусть при повороте на угол α точка P0 (1; 0) переходит в точку Pα (x; y)
(то есть при повороте на угол α радиус OP0 переходит в радиус OPα) (рис. 63).
Синусом угла α называется ордината точки Pα (x; y) единичной окружности:
sin α = y.
Косинусом угла α называется абсцисса точки Pα (x; y) единичной окружности:
cos α = x.
Тангенсом угла α называется отношение ординаты точки Pα (x; y) единичной окружности к ее абсциссе, то есть отношение sin α / cos α.
Таким образом, tg α = sin α / cos α (где cos α ≠ 0).
Заметим, что при cos α = 0 значение функции tg α не определено, а значение функции ctg α не определено при sin α = 0.
Пользуясь этими определениями, найдем синус, косинус, тангенс и котангенс угла 2π / 3 радиан.
♦ Рассмотрим единичную окружность (рис. 64). При повороте на угол 2π / 3 радиус OP0 переходит в радиус OP2π/3 (а точка P0 переходит в точку P2π/3). Координаты точки P2π/3 можно найти, используя свойства прямоугольного треугольника OAP2π/3 (с углами 60° и 30° и гипотенузой 1): x = — OA=−1/2; y = AP2π/3 = √3/2. Тогда: sin 2π/3 = y = √3/2; cos 2π/3 = x = -1/2; tg 2π/3 = sin 2π/3 / cos 2π/3 = — √3; ctg 2π/3 = — 1/√3.◊
Аналогично находятся значения синуса, косинуса, тангенса и котангенса углов, градусные и радианные меры которых указаны в верхней строке таблицы 19 (с. 156).
Укажем, что таким образом можно найти тригонометрические функции только некоторых углов. Тригонометрические функции произвольного угла обычно находят с помощью калькулятора или таблиц.
2. Тригонометрические функции числового аргумента. Введенные определения позволяют рассматривать не только тригонометрические функции углов, но и тригонометрические функции числовых аргументов, если рассматривать тригонометрические функции числа α как соответствующие тригонометрические функции угла в α радиан. То есть:
синус числа α — это синус угла в α радиан;
косинус числа α — это косинус угла в α радиан.
Например: sin π/6 = sin (π/6 радиан) = sin 30° = 1/2 (см. также пункт 2 табл. 7).
Таблица 19
| α | градусы | 0º | 30º | 45º | 60º | 90º | 180º | 270º | 360º |
| радианы | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 | |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 | |
| tg α | 0 | √3/3 | 1 | √3 | — | 0 | — | 0 | |
| ctg α | — | √3 | 1 | √3/3 | 0 | — | 0 | — |
3. Линии тангенсов и котангенсов. Для решения некоторых задач полезно иметь представление о линиях тангенсов и котангенсов.
♦ Проведем через точку P0 единичной окружности прямую AP0, параллельную оси Oy (рис. 65). Эта прямая называется линией тангенсов.
Пусть α — произвольное число (или угол), для которого cos α ≠ 0. Тогда точка Pα не лежит на оси Oy и прямая OPα пересекает линию тангенсов в точке A. Поскольку прямая OPα проходит через начало координат, то ее уравнение имеет вид y = kx. Но эта прямая проходит через точку Pα с координатами (cos α; sin α), значит, координаты точки Pα удовлетворяют уравнению прямой y = kx, то есть sin α = k cos α. Отсюда k = sin α / cos α = tg α. Следовательно, прямая OPα имеет уравнение
y = (tg α) x. Прямая AP0 имеет уравнение x = 1. Чтобы найти ординату точки A, достаточно в уравнение прямой OPα подставить x = 1. Получаем yA = tg α. Таким образом,
тангенс угла (числа) α — это ордината соответствующей точки на линии тангенсов.◊
Аналогично вводится и понятие линии котангенсов: это прямая CB (рис. 66), которая проходит через точку C (0; 1) единичной окружности параллельно оси Ox.
Если α — произвольное число (или угол), для которого sin α ≠ 0 (то есть точка Pα не лежит на оси Ox), то прямая OPα пересекает линию котангенсов в некоторой точке B (xB; 1).
Аналогично вышеизложенному обосновывается, что xB = ctg α, таким образом,
котангенс угла (числа) α — это абсцисса соответствующей точки на линии котангенсов.
Вопросы для контроля
1. Сформулируйте определения тригонометрических функций острого угла в прямоугольном треугольнике.
2. Сформулируйте определения тригонометрических функций произвольного угла:
а) используя окружность радиуса R с центром в начале координат;
б) используя единичную окружность.
3. Что имеют в виду, когда говорят о синусе, косинусе, тангенсе и котангенсе числа α?
Упражнения
1°. Постройте на единичной окружности точку Pα, в которую переходит точка P0 (1; 0) единичной окружности при повороте на угол α. В какой координатной четверти находится точка Pα в заданиях 3–6?
1) α = 3π; 2) α = –4π; 3) α=7π/6;
4) α=−3π/4; 5) α=4π/3; 6) α=7π/4.
2. Найдите значение sin α, cos α, tg α, ctg α (если они существуют) при:
1) α = 3π; 2) α = –4π; 3) α=−π/2;
4) α=5π/2; 5*) α=−5π/6; 6*) α=3π/4.
3°. Пользуясь определением синуса и косинуса, с помощью единичной окружности укажите знаки sin α и cos α, если:
1) α=6π/5; 2) α=−π/6; 3) α=5π/6;
4) α=−2π/3; 5) α=π/10.
4*. Пользуясь линией тангенсов, укажите знак tg α, если:
1) α=4π/3; 2) α=−3π/4; 3) α=11π/6;
4) α=−7π/6; 5) α=9π/4.
5*. Пользуясь линией котангенсов, укажите знак сtg α, если:
1) α=−4π/3; 2) α=3π/4; 3) α=−11π/6;
4) α=7π/6; 5) α=−9π/4.
Уравнение прямой, содержащей сторону АВ:
АВ: (х — 2)/6 = (у — 3)/6. Уравнение АВ: у = х + 1.
Высота СД — это перпендикуляр к АВ. к(СД) = -1/к(АВ) = -1/1 = -1.
Уравнение СД: у = -х + в. Подставим координаты точки С:
2 = -1*7 + в, отсюда в = 2 + 7 = 9.
Уравнение СД: у = -х + 9.
Точка Д одновременно принадлежит АВ и СД, приравняем уравнения:
х + 1 = -х + 9,
2х = 8,
х = 8/2 = 4.
у = 4 + 1 = 5. Это ответ.
Приложения:
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Содержание:
В этой лекции вы узнаете, что представляют собой синус, косинус и тангенс угла
Решение треугольников
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам).
Синус, косинус и тангенс угла от 0 до 180
Понятия синуса, косинуса и тангенса острого угла вам известны из курса геометрии 8 класса. Расширим эти понятия для произвольного угла 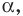
В верхней полуплоскости координатной плоскости рассмотрим полуокружность с центром в начале координат, радиус которой равен 1 (рис. 1.1). Такую полуокружность называют единичной.
Будем говорить, что углу 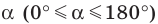
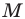
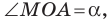
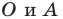
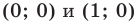

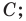
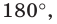
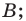
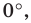
Пусть 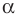
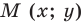
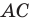
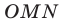
Поскольку 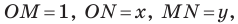
Итак, косинус и синус острого угла 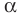
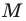
Полученный результат подсказывает, как определить синус и косинус произвольного угла 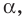
Определение. Косинусом и синусом угла 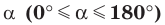
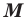
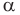
Пользуясь этим определением, можно, например, установить, что
Если 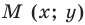
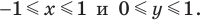
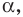
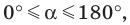
Если 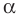
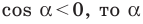
Из курса геометрии 8 класса вы знаете, что для любого острого угла а выполняются равенства:
Эти формулы остаются справедливыми также для 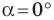
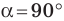
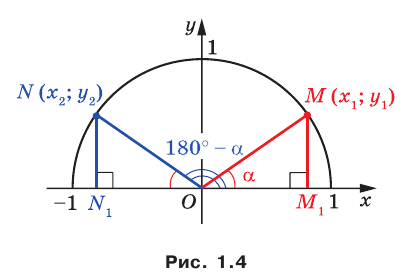
Пусть углам 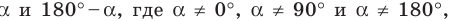
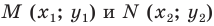
Прямоугольные треугольники 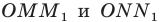
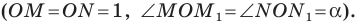
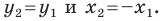
Убедитесь самостоятельно, что эти равенства остаются верными для
Если 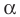
Это равенство остается верным для 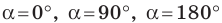
Пусть 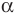
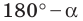
Следовательно, равенство 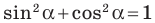
Определение. Тангенсом угла 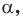
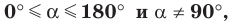
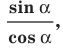
Поскольку 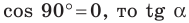
Очевидно, что каждому углу 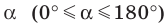
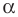
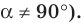
Функции 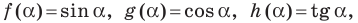
Пример №1
Докажите, что
Решение:
Пример №2
Найдите
Решение:
Имеем:
Теорема косинусов
Из первого признака равенства треугольников следует, что две стороны и угол между ними однозначно определяют треугольник. А значит, по указанным элементам можно, например, найти третью сторону треугольника. Как это сделать, показывает следующая теорема.
Теорема 2.1 (теорема косинусов). Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
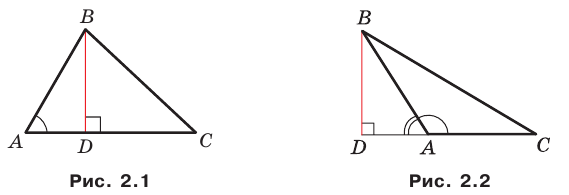
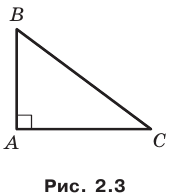
Доказательство: Рассмотрим треугольник 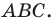
Возможны три случая:
- угол
острый;
- угол
тупой;
- угол
прямой.
Первый случай. Пусть угол 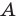
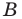
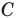
Пусть 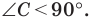
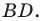
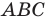
В прямоугольном треугольнике
Пусть 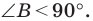

Второй случай. Пусть угол 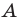
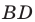
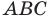
В прямоугольном треугольнике
В прямоугольном треугольнике BDC:
Третий случай. Пусть угол 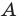
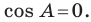
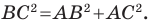
Доказательство теоремы косинусов показывает, что теорема Пифагора является частным случаем теоремы косинусов, а теорема косинусов является обобщением теоремы Пифагора.
Если воспользоваться обозначениями для длин сторон и величин углов треугольника 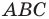
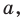
С помощью теоремы косинусов, зная три стороны треугольника, можно определить, является ли он остроугольным, тупоугольным или прямоугольным.
Теорема 2.2 (следствие из теоремы косинусов). Пусть 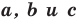
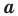
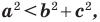
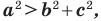
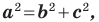
Доказательство: По теореме косинусов
Отсюда
Пусть 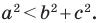
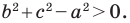

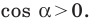
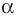
Поскольку 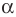
Пусть 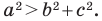
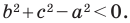

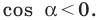
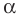
Пусть 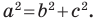

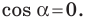
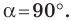
Пример №3
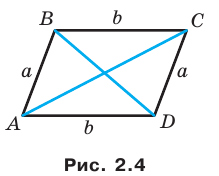
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Решение:
На рисунке 2.4 изображен параллелограмм 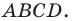
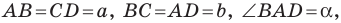
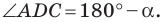
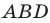
Из треугольника 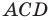
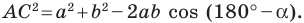
Сложив равенства (1) и (2), получим:
Пример №4
В треугольнике 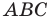
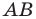
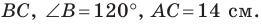
Решение:
По теореме косинусов
Пусть 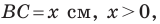
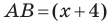
Имеем:
Корень -10 не удовлетворяет условию
Следовательно,
Ответ:
Пример №5
На стороне 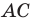
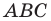
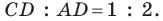
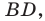
Решение:
По теореме косинусов из треугольника 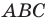
Отсюда
Поскольку 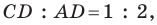
Тогда из треугольника 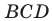
Следовательно,
Ответ:
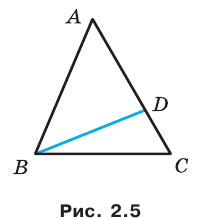
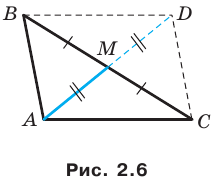
Пример №6
Две стороны треугольника равны 23 см и 30 см, а медиана, проведенная к большей из известных сторон, — 10 см. Найдите третью сторону треугольника.
Решение:
Пусть в треугольнике 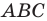
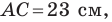
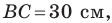
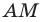
На продолжении отрезка 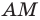
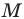
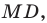
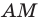
В четырехугольнике 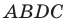
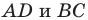
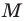
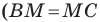
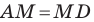
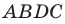
Так как сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон (см. ключевую задачу 1), то
Тогда
Ответ: 11 см.
Теорема синусов
При доказательстве ряда теорем и решении многих задач применяют следующую лемму.
Лемма. Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду.
Доказательство: На рисунке 3.1 отрезок 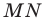
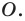
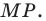
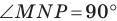
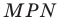
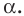
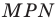
Все вписанные углы, опирающиеся на хорду 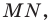
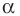
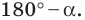
Из второго признака равенства треугольников следует, что сторона
и два прилежащих к ней угла однозначно определяют треугольник. Следовательно, по указанным элементам можно найти две другие стороны треугольника. Как это сделать, подсказывает следующая теорема.
Теорема 3.1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство: Пусть в треугольнике 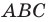
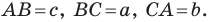
Пусть радиус описанной окружности треугольника 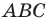
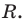
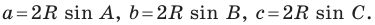
Следствие. Радиус окружности, описанной около треугольника, можно вычислить по формуле
где 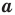
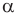
Пример №7
В треугольнике 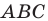
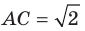
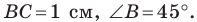
Решение:
По теореме синусов
Тогда
Поскольку 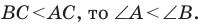
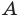
Отсюда, учитывая, что 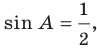
Ответ:
Пример №8
В треугольнике 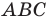
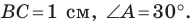
Решение:
По теореме синусов 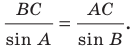
Поскольку 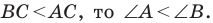
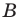
Ответ:
Пример №9
На стороне 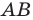
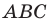
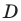
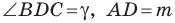
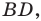
Решение:
Угол 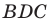
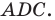
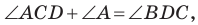
Из треугольника 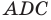
Следовательно,
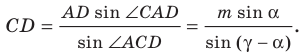
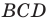
Следовательно,
Ответ:
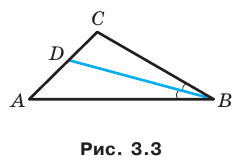
Пример №10
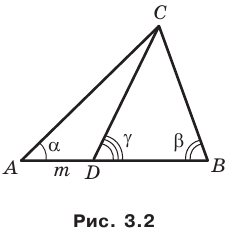
Отрезок 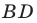
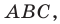
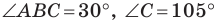
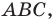
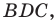
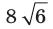
Решение:
Пусть 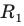
Поскольку отрезок 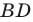
Из треугольника 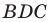
По следствию из теоремы синусов 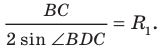
Из треугольника 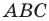
Пусть 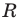
Тогда 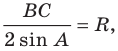
Ответ:
Как решать треугольников
Решить треугольник — это значит найти неизвестные его стороны и углы по известным сторонам и углам
Теоремы косинусов и синусов позволяют решить любой треугольник.
В следующих задачах значения тригонометрических функций будем находить с помощью калькулятора и округлять эти значения до сотых. Величины углов будем находить с помощью калькулятора и округлять эти значения до единиц. Вычисляя длины сторон, результат будем округлять до десятых.
Пример №11
Решите треугольник (рис. 4.1) по стороне 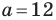
Решение:
Используя теорему о сумме углов треугольника, получаем:
По теореме синусов
Отсюда
Имеем:
Вновь применяя теорему синусов, запишем:
Отсюда
Имеем:
Ответ:
Пример №12
Решите треугольник по двум сторонам 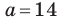
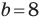
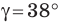
Решение:
По теореме косинусов
Отсюда
Далее имеем:
Отсюда
Используя теорему о сумме углов треугольника, получаем:
Ответ:
Пример №13
Решите треугольник по трем сторонам 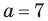
Решение:
По теореме косинусов 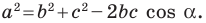
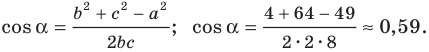
Пo теореме синусов 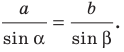
Поскольку 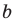
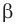
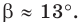
Ответ:
Пример №14
Решите треугольник по двум сторонам и углу, противолежащему одной из сторон:
Решение:
1) По теореме синусов
Отсюда
Поскольку угол 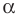
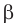
Используя теорему о сумме углов треугольника, получаем:
По теореме синусов
Отсюда
Ответ:
2) По теореме синусов
Отсюда 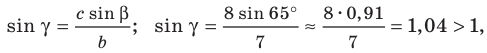
Ответ: задача не имеет решения.
3) По теореме синусов 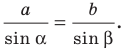
Возможны два случая: 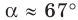
Рассмотрим случай, когда
Используя теорему о сумме углов треугольника, получаем:
Пo теореме синусов
Отсюда 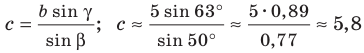
Рассмотрим случай, когда
Используя теорему о сумме углов треугольника, получаем:
Поскольку 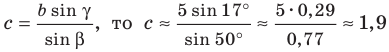
Ответ:
Тригонометрия наука об измерении треугольников
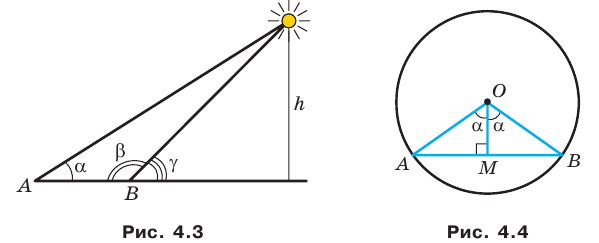
Вы знаете, что древние путешественники ориентировались по звездам и планетам. Они могли достаточно точно определить положение корабля в океане или каравана в пустыне по расположению светил на небосклоне. При этом одним из ориентиров служила высота, на которую поднималось над горизонтом то или иное небесное светило в данной местности в данный момент времени.
Понятно, что непосредственно измерить эту высоту невозможно. Поэтому ученые стали разрабатывать методы косвенных измерений. Здесь существенную роль играло решение треугольника, две вершины которого лежали на поверхности Земли, а третья являлась звездой (рис. 4.3) — знакомая вам задача 3.17.
Для решения подобных задач древним астрономам необходимо было научиться находить взаимосвязи между элементами треугольника. Так возникла тригонометрия — наука, изучающая зависимость между сторонами и углами треугольника. Термин «тригонометрия» (от греческих слов «тригонон» — треугольник и «метрео» — измерять) означает «измерение треугольников».
На рисунке 4.4 изображен центральный угол 
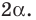
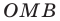
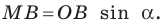
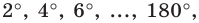
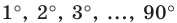
Измеряя длины полухорд, древнегреческий астроном Гиппарх (II в. до н. э.) составил первые тригонометрические таблицы.
Понятия синуса и косинуса появляются в тригонометрических трактатах индийских ученых в IV-V вв. н. э. В X в. арабские ученые оперировали понятием тангенса, которое возникло из потребностей гномоники — учения о солнечных часах (рис. 4.5).
В Европе первой работой, в которой тригонометрия рассматривалась как отдельная наука, был трактат «Пять книг о треугольниках всех видов», впервые напечатанный в 1533 г. Его автором был немецкий ученый Региомонтан (1436-1476). Этот же ученый открыл и теорему тангенсов:
где 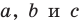
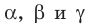
Современный вид тригонометрия приобрела в работах великого математика Леонарда Эйлера.
Леонард Эйлер
(1707-1783) Выдающийся математик, физик, механик и астроном, автор более 860 научных работ. Член Петербургской, Берлинской, Парижской академий наук, Лондонского королевского общества, многих других академий и научных обществ. Имя Эйлера встречается почти во всех областях математики: теоремы Эйлера, тождества Эйлера, углы, функции, интегралы, формулы, уравнения, подстановки и т. д.
Формулы для нахождения площади треугольника
Из курса геометрии 8 класса вы знаете, что площадь 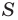
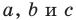
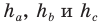
Теперь у нас появилась возможность получить еще несколько формул для нахождения площади треугольника.
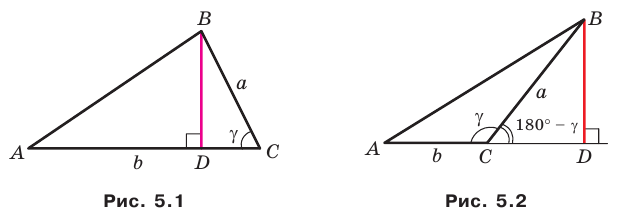
Теорема 5.1. Площадь треугольника равна половине произведения двух его сторон и синуса угла между ними.
Доказательство: Рассмотрим треугольник 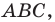
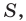
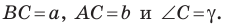
Возможны три случая:
- угол
острый (рис. 5.1);
- угол
тупой (рис. 5.2);
- угол
прямой.
На рисунках 5.1 и 5.2 проведем высоту 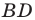
Тогда
Из прямоугольного треугольника 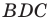
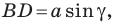
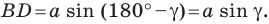
Если угол 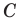
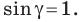
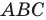
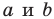
Теорема 5.2 (формула Герона
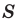
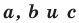
где 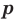
Доказательство: Рассмотрим треугольник 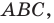
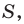
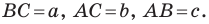
Пусть 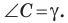
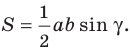
По теореме косинусов 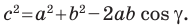
Поскольку 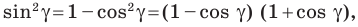
Отсюда
Теорема 5.3. Площадь 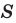
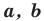
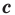
где 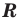
Доказательство: Рассмотрим треугольник 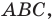
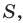
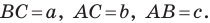
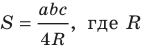
Пусть 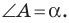
Из леммы п. 3 следует, что
Тогда
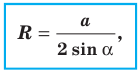
Заметим, что доказанная теорема позволяет находить радиус описанной окружности треугольника по формуле
Теорема 5.4. Площадь треугольника равна произведению его полупериметра и радиуса вписанной окружности.
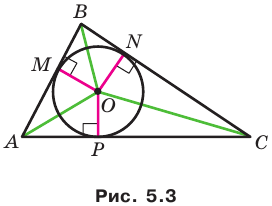
Доказательство: На рисунке 5.3 изображен треугольник 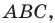
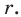
где 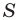
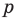
Пусть точка 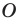
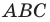
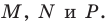
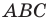
Проведем радиусы в точки касания. Получаем: 
Следовательно,
Теорему 5.4 обобщает следующая теорема.
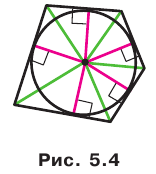
Теорема 5.5. Площадь описанного многоугольника равна произведению его полупериметра и радиуса вписанной окружности.
Докажите эту теорему самостоятельно (рис. 5.4).
Заметим, что теорема 5.5 позволяет находить радиус вписанной окружности многоугольника по формуле
Пример №15
Докажите, что площадь 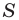
где 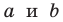
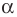
Решение:
Рассмотрим параллелограмм 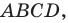
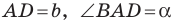
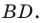
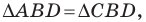
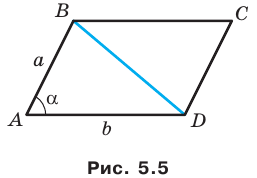
Пример №16
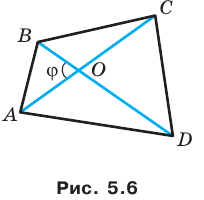
Докажите, что площадь выпуклого четырехугольника равна половине произведения его диагоналей и синуса угла между ними.
Решение:
Пусть угол между диагоналями 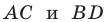
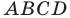
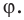
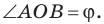
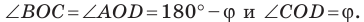
Пример №17
Стороны треугольника равны 17 см, 65 см и 80 см. Найдите наименьшую высоту треугольника, радиусы его вписанной и описанной окружностей.
Решение:
Пусть
Найдем полупериметр треугольника:
Площадь треугольника вычислим по формуле Герона:
Наименьшей высотой треугольника является высота, проведенная к его наибольшей стороне, длина которой равна
Поскольку
Радиус вписанной окружности
Радиус описанной окружности
Ответ:
Вневписанная окружность треугольника
Проведем биссектрисы двух внешних углов с вершинами 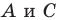
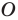
Проведем три перпендикуляра: 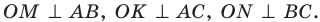
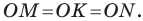
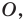
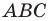
Поскольку 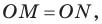
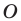
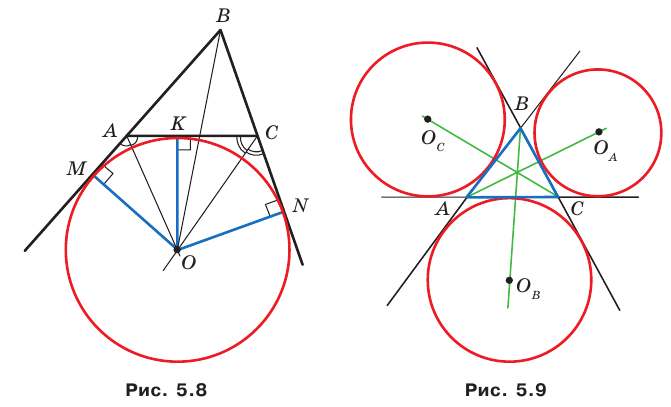
Любой треугольник имеет три вневписанные окружности. На рисунке 5.9 их центры обозначены 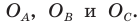
По свойству касательных, проведенных к окружности через одну точку, имеем: 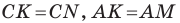
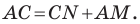
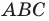
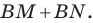
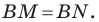
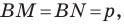
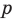
Имеем:
Отсюда 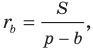
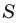
Аналогично можно показать, что
Справочный материал
Косинус и синус
Косинусом и синусом угла 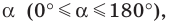
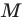
Тангенс
Тангенсом угла 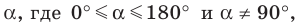
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними:
Следствие из теоремы косинусов
Пусть 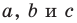
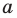
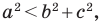
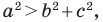
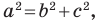
Лемма о хорде окружности
Хорда окружности равна произведению диаметра и синуса любого вписанного угла, опирающегося на эту хорду.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов:
Формулы для нахождения площади треугольника
Формула Герона:
Формула для нахождения радиуса окружности, вписанной в треугольник
Формулы для нахождения радиуса окружности, описанной около треугольника
Площадь многоугольника, описанного около окружности
Площадь многоугольника, описанного около окружности, равна произведению его полупериметра и радиуса вписанной окружности.
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры — виды, изображения, свойства
- Взаимное расположения прямых на плоскости
- Треугольник

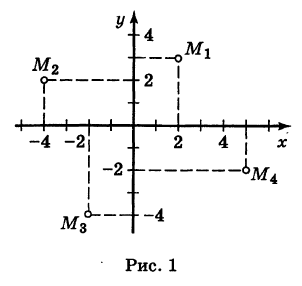
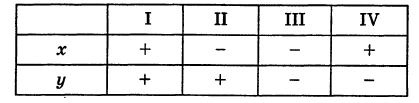
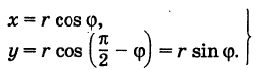

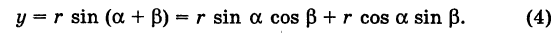
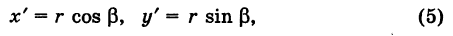
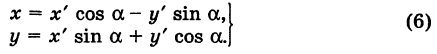
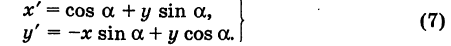
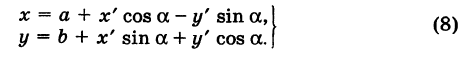
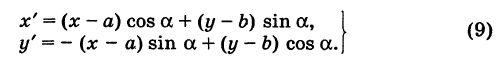


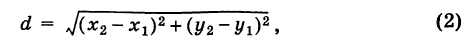
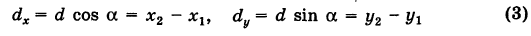
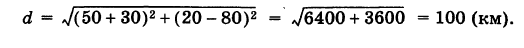

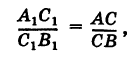

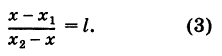
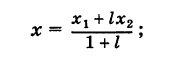
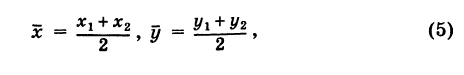
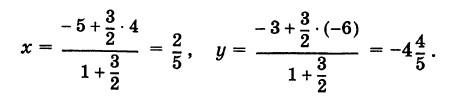
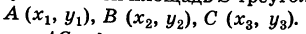
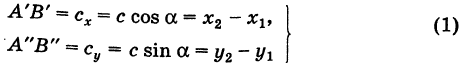
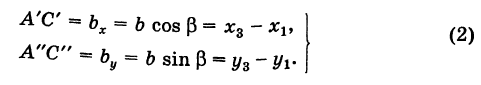
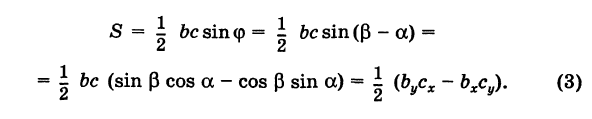
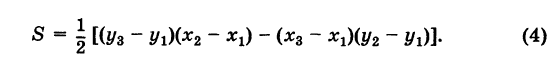
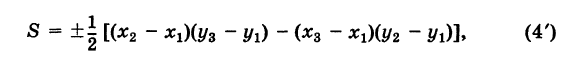
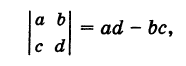
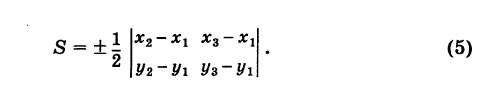
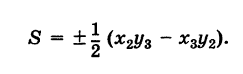
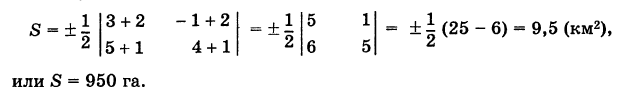





















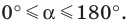
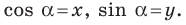
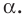

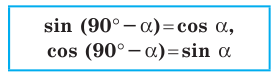



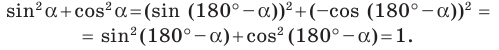
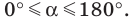

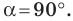
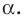
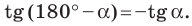
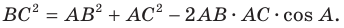
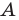 острый;
острый;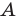 тупой;
тупой;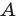 прямой.
прямой.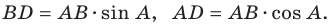
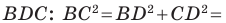
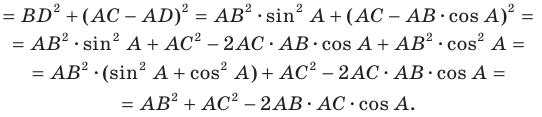
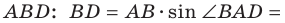
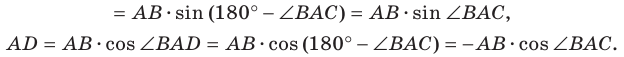
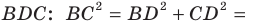
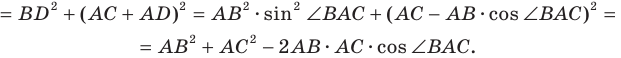
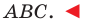
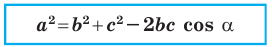
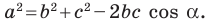
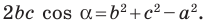
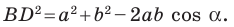
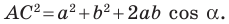
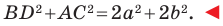
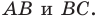
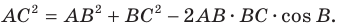
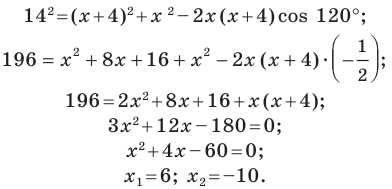
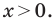
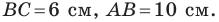
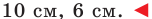
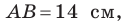
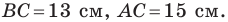
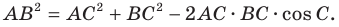
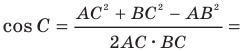
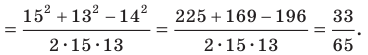
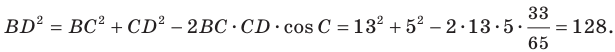
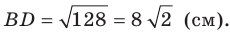
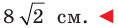
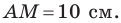
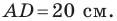
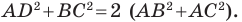
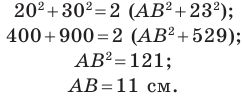

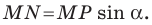
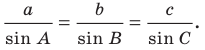
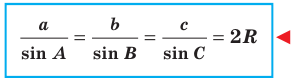
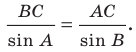
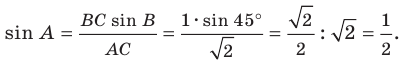
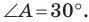
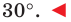
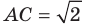
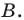
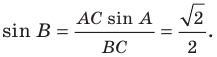
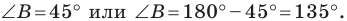
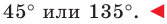
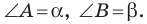
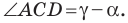
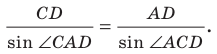
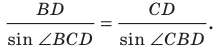
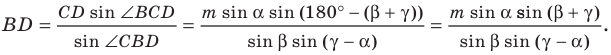
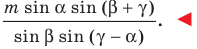
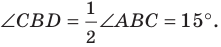
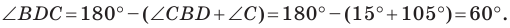
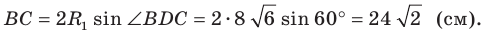
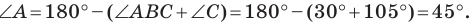
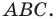
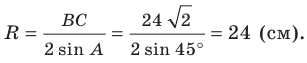
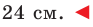
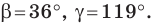
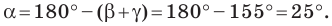
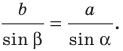
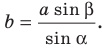
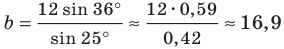
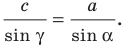
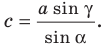
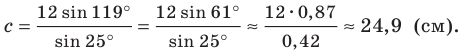
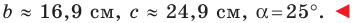
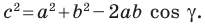
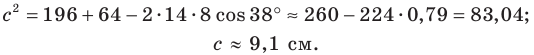
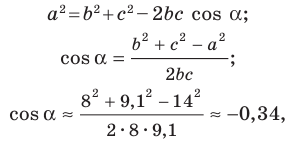
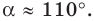
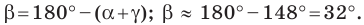
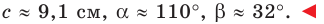
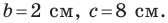
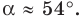
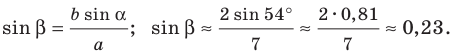
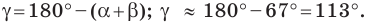
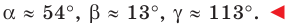
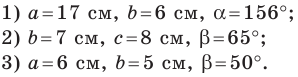
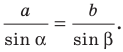
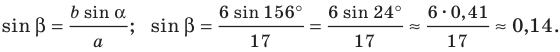
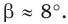
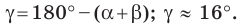
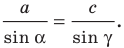
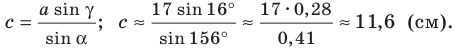
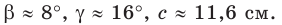
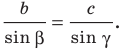
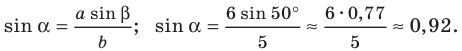
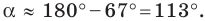
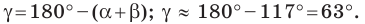
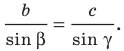
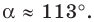
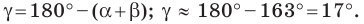
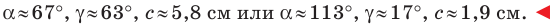

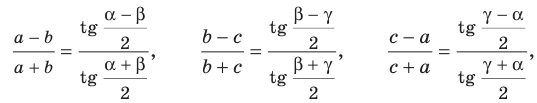
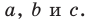

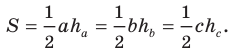
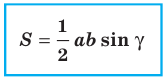
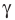 острый (рис. 5.1);
острый (рис. 5.1);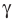 тупой (рис. 5.2);
тупой (рис. 5.2); прямой.
прямой.