Первые шаги в ОТО: прецессия орбиты Меркурия
Время на прочтение
9 мин
Количество просмотров 15K
Когда речь заходит о теории относительности, частенько на ровном месте разрастаются споры, которые были занесены в почву непонимания и обильно удобрены мифами, недосказанностью и недостаточной математической подготовкой. Даже на лекциях от некоторых профессоров можно услышать, что детище гения Эйнштейна не имеет практической пользы, а на робкие попытки пролепетать что-то про спутниковые системы навигации они пренебрежительно отмахиваются, дескать, там все сложно и двояко.
Так что совершенно естественно желание попробовать провести некоторые расчеты самолично, потрогать формулы, покрутить параметры, чтобы постепенно заложить интуицию в столь горячей теме.
Вся красота и непостижимая мощь общей теории относительности аккуратно упакована в уравнение гравитационного поля Эйнштейна:
Оно говорит, что искривление пространства-времени определяется материей. То есть, гравитация воспринимается не как сила, а как следствие искривленной геометрии царства 4d, а искривления порождены материей (тензор энергии-импульса в правой части уравнения). Движению объекта можно поставить в соответствие траекторию в четырехмерном пространстве-времени — мировую линию. Просто представьте себе четырехмерный брусок в котором статично зависли макаронины: галактики, планеты или молекулы — последние на некоторое мгновение переплетаются, чтобы образовать читателя этой статьи, а затем вновь разносятся в пространстве, очерчивая пути кусочков кожи и турбулентных потоков выдохнутого воздуха.
Вся эта лапша подчинена кривизне пространства-времени, и она же, собираясь в массивные сплетения, эту кривизну задает. Для работы с искривленной геометрией у нас есть математические инструменты: метрический тензор, символы Кристоффеля, тензор кривизны Римана, тензор Риччи и скалярная кривизна. Для того, чтобы создать интуитивный образ, вообразите натянутый кусок ткани деформированный массивным телом…
Хотя есть куда более умозрительный и математически точный вариант в видео A new way to visualize General Relativity:
И давайте тогда сразу приведем список полезных источников для погружения в тему:
видео и книги
-
Вспомнить специальную теорию относительности помогут видео от MinutePhysics на русском.
-
Вспоминаем сущность линейной алгебры с 3Blue1Brown.
-
Постигаем магию тензорной алгебры с серией статей на хабре.
-
Вывод уравнения Эйнштейна смотрим в Einstein Field Equations — for beginners!
-
Понять математику ОТО поможет серия The Maths of General Relativity от ScienceClic English (настойчиво советую просмотреть весь материал канала − на редкость качественная постановка и визуализация сложных тем),
-
книжки Introduction to general relativity 2010, Gerard ’t Hooft, A first course in general relativity 2009 Schutz, General Relativity, Black Holes, and Cosmology 2020, Andrew J. S. Hamilton
-
и более щадящая Cosmology, Daniel Baumann
-
Видео VSauce: вниз — это куда? если вы боитесь формул.
На русском книг не предложу, но, думаю, если мы хором позовем @Tyusha, то она может чего посоветовать.
Орбиты в геометрии Шварцшильда
Все мы со школьной скамьи приучены к метрике Минковского: решая задачки в евклидовой геометрии, постепенно привыкаешь к плоскому пространству. Но чего нам действительно не хватало, так это построения геодезических линий на глобусе или небесной сфере. Собственно, сферическая симметрия это вотчина метрики Шварцшильда. Гравитационное поле массивного сферического тела, черные дыры — это все сюда. Есть еще разные другие метрики: для заряженных, для вращающихся тел, для расширяющейся вселенной и т. д.
В плоском пространстве-времени все довольно просто:
-
Событие задается вектором с четырьмя компонентами
-
Зависящие от наблюдателя пространственно-временные координаты превращаются в инвариантные линейные элементы с помощью тензора метрики (мы держим в уме соглашение Эйнштейна о суммировании и Лоренц-инвариантность)
-
Тензор метрики Минковского — это диагональная матрица 4х4
-
Определяем интервал в этом плоском четырехмерьи. Обобщение теоремы Пифагора в искривленное пространство-время.
-
Записываем его через собственное время — часики-то тикают, и у каждого свои.
-
Вводим 4d-скорость. dx/dτ — скорость движения в направлении оси Х, dt/dτ — скорость изменения временнóй компоненты и т.д.
Допустим мы хотим решить уравнение Эйнштейна (найти метрический тензор g_{μν} ) для точки на некотором удалении от статичного незаряженного сферического тела. Само по себе решение в лоб трудоемко, но правильный выбор системы координат и учет симметрий чрезвычайно упрощают получение результата. Так что вывод метрики Шварцшильда вполне посильный труд. Получается, расстояние между двумя событиями в пространстве-времени в окрестности массивного сферического тела в вакууме имеет форму
Если занулить массу М, получим пустое плоское пространство-время Минковского. Чем ближе мы к массивному телу, тем сильнее ощущаем кривизну. Внутри тела метрика не работает, но если оно компактное, то мы можем найти особое положение, при котором первое слагаемое стремится к нулю, и, соответственно, второе уходит в бесконечность. Как вы догадались, речь идет о радиусе Шварцшильда — горизонте черной дыры. Для разогрева, попробуйте рассчитать в этой метрике замедление времени для искусственного спутника Земли и сравните с результатами какого-нибудь эксперимента.
Запишем тензор метрики в нормальных единицах (c=G=1). Кстати, в этой геометрической системе время и масса имеют размерность длины. Ответьте, чему равен ваш возраст в метрах? А сколько километров весит Солнце?
Воспользуемся симметрией смещения во времени и вращения вокруг оси z, чтобы ввести сохраняющиеся величины:
Это энергия и угловой момент на единицу массы покоя. К слову, они нам еще могут пригодиться, если мы вдруг надумаем поиграть с черными дырами и червоточинами. Итак, сохранение углового момента подразумевает, что орбита лежит в заданной плоскости, что позволяет выбрать для переменной θ конкретное значение, скажем θ = π/2. Чтобы перейти к скоростям, разделим выражение для интервала в метрике Шварцшильда на dτ² и получим выражение для полной энергии тела на орбите
Уравнение полной энергии слагается из кинетической и потенциальной, так что у нас есть аналитическое выражение для гравитационного потенциала в релятивистском и классическом случаях.
Давайте их визуализируем! Используем язык Julia (для питонистов в конце тоже будет ссылка).
Код
using Plots
const AU = 1.49597870700e11 # m. Astronomical Unit (distance Earth-Sun)
const T = 365.25*3600*24 # s. 1 year
const c = 2.99792458e8 # AU/yr. Speed of light
const G = 6.67408e-11 # m^3/kg s^2. Gravitational constant
const M = 1.989e30; # kg. Solar mass
Veff(ρ, l) = return 0.5*( (l/ρ)^2 - 1.0/ρ - l^2/ρ^3 )
Vclassical(ρ, l) = return 0.5*( (l/ρ)^2 - 1.0/ρ )
N = 1000
rho = range(1, stop = 30, length = N)
l = 2
# Evaluate potentials
VGR = Veff.(rho, l)
VCM = Vclassical.(rho, l)
# Max/min
# Classical mechanics
rhoCM_min = 2*l^2
VCM_min = -0.125/l^2
# General relativity
rho_min = l^2 + l*sqrt(l^2 - 3)
VGR_min = Veff.(rho_min, l)
rho_max = l^2 - l*sqrt(l^2 - 3)
VGR_max = Veff.(rho_max, l)
# Potentials
plot( rho, VGR, label="GR", line = 3)
plot!(rho, VCM, label="CM", line = 3)
# Three different types of orbits
edge = VGR_max - VGR_min
hline!([VGR_max + edge/6], line=(2, :dash, :purple),label="Orbit 1")
hline!([(VGR_max + VGR[end])/2], line=(2,:dashdot,:purple),label="Orbit 2")
hline!([(VCM_min + VGR[end])/2], line=(2, :dot, :purple),label="Orbit 3")
# Extremum
scatter!([rhoCM_min, rho_min, rho_max],
[VCM_min, VGR_min, VGR_max], label="Extremum")
# Axes settings
yaxis!( "V", (VGR_min - edge/3, VGR_max + edge/3) )
xaxis!( "\rho = r / R_S" )Окей, как и предполагалось, в классической механике существует только два различных типа орбит:
-
замкнутые: эллипсы и круги (орбиты 2 и 3)
-
незамкнутые орбиты рассеяния: гиперболы (орбита 1)
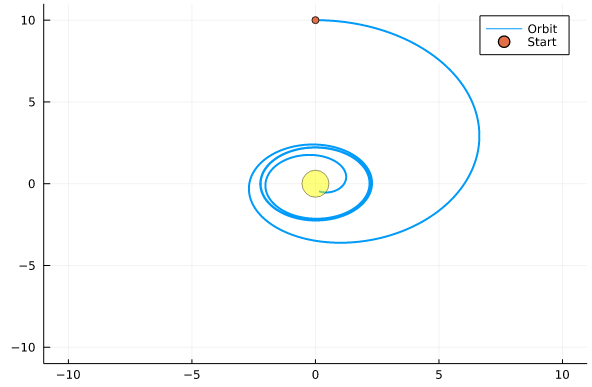
В общей теории относительности существует три типа орбит:
-
спиральные: радиальное погружение (орбита 1)
-
незамкнутые (орбита 2)
-
замкнутые: прецессирующие эллипсы (орбита 3)
Очевидно, устойчивость орбиты определяется характером экстремума.
Уравнения движения
Вспомним формулу полной энергии и запишем ее в привычной размерной форме
Заметим, что при малых скоростях четвертое слагаемое дает пренебрежимо малый вклад, и формула будет описывать классическое орбитальное движение. А дальше, выполнив дифференцирование последних двух слагаемых, имеем радиальную силу
Опять-таки, в классическом случае, когда скорость света кажется бесконечной, у нас будет обычная формула из школьной физики. Вспомнив второй закон Ньютона, записываем уравнение движения
или, на плоскости и с понижением порядка:
Здесь появились константы А и В, чтобы можно было переобозначив их легко вернуться к размерным переменным. Четыре дифурки решаем Рунге-Куттой-4:
Код
getB(Z) = 3*(Z[1]*Z[4] - Z[2]*Z[3])^2
getA() = 0.5
function RHS(Z, A, B) # right-hand side of equation
rho = sqrt(Z[1]^2 + Z[2]^2)
correction = 1 + B/rho^2
dUdτ = -A*Z[1]/rho^3 * correction
dVdτ = -A*Z[2]/rho^3 * correction
return [ Z[3], Z[4], dUdτ, dVdτ ]
end
function rk4step(f, y, h, A, B)
s1 = f(y, A, B)
s2 = f(y + 0.5h*s1, A, B)
s3 = f(y + 0.5h*s2, A, B)
s4 = f(y + h*s3, A, B)
return y + h/6.0*(s1 + 2s2 + 2s3 + s4)
end
function getOrbit(n, T_max, Z0)
B = getB(Z0)
A = getA()
#println("GR correction constant: $B")
h = T_max/n
Z = zeros(n, 4)
Z[1,:] = Z0
for i in 1:n-1
Z[i+1, :] = rk4step(RHS, Z[i,:], h, A, B)
#if abs(Z[i+1,1])<h && abs(Z[i+1,2])<2 break end
end
return Z
end
function plotOrbit(Z, lim_fact)
plot(Z[:,1], Z[:,2], label="Orbit", line = 2)
scatter!([Z[1]], [Z[1,2]], label="Start")
ax_lim = max(Z[1], Z[1,2])
xaxis!( (-lim_fact*ax_lim, lim_fact*ax_lim) )
yaxis!( (-lim_fact*ax_lim, lim_fact*ax_lim) )
scatter!([0], [0], label="", m = (15, 0.5, :yellow) )
end
anim = @animate for d ∈ 0.04:0.005:0.14
Z0 = [ 0, 10, 0.1+d, -2d ]
n = 8000
tau_max = 3000
Z = getOrbit(n, tau_max, Z0)
plotOrbit(Z, 1.1)
end
gif(anim, "orbits.gif", fps = 6)и давайте нарисуем все три типа релятивистских орбит
#Z0 = [0, 10, .1845, 0]
Z0 = [0, 10, .1849, 0]
n = 5000
tau_max = 142.7
Z = getOrbit(n, tau_max, Z0)
p1 = plotOrbit(Z, 1.1)Z0 = [0, 20, 0.1, 0]
#Z0 = [0, 10, 0.2, -0.2]
#Z0 = [0, 10, .25, 0]
#Z0 = [0, 10, 0.2, -.1]
#Z0 = [0, 10, .2, 0]
n = 5000
tau_max = 4000
Z = getOrbit(n, tau_max, Z0)
p2 = plotOrbit(Z, 1.1)#Z0 = [0, 100, 0.05, -0.5]
Z0 = [0, 10, 0.2, -.25]
n = 5000
tau_max = 1000
Z = getOrbit(n, tau_max, Z0)
p3 = plotOrbit(Z, 1.1)Что будет если стартануть с горизонта событий? С позиции за горизонтом? Что произойдет при достижении r = 0?
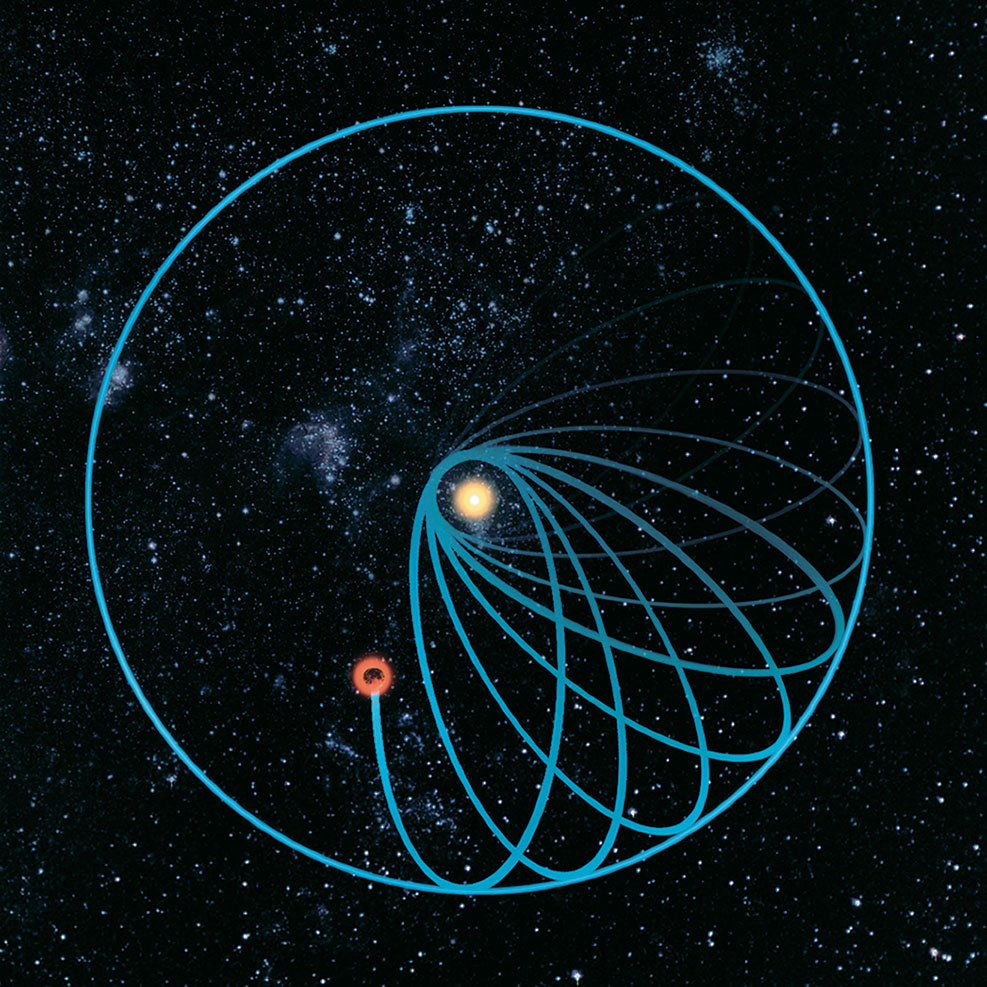
Смещения перигелия Меркурия
Каждое столетие перигелий орбиты Меркурия увеличивается на 5300 угловых секунд, но только около 5260 угловых секунд могут быть объяснены ньютоновской механикой. Да, были способы разной степени костыльности, но наша цель — проверить, может ли общая теория относительности объяснить оставшиеся 40 угловых секунд.
Запишем уравнение движения в форме удобной для подстановки измеряемых констант:
Здесь R = 1 AU расстояние между Землей и Солнцем, T = 1 земной год, m — масса Меркурия, M — масса Солнца. Еще полезно будет знать ряд измеримых параметров:
|
Меркурий |
|
|
Перигелий |
0.307 499 АЕ |
|
Афелий |
0.466 697 АЕ |
|
Год |
0.240 846 земн. лет |
|
Макс. орбитальная скорость |
58.98 км/с |
|
Мин. орбитальная скорость |
38.86 км/с |
В перигелии скорость максимальна. В афелии она минимальна. В обоих случаях скорость нормальна к вектору расстояния между Солнцем и Меркурием.
Присмотримся к константе B. Эта величина характеризуется небольшим числом, что означает, что общая релятивистская поправка на ньютонову орбиту невелика. На самом деле, если мы продолжим наивно вычислять орбиту Меркурия, интегрируя уравнение движения, мы получим неправильную скорость прецессии из-за ошибок численного округления. Поэтому мы рассмотрим различные значения для B для набора орбит с более высокой скоростью прецессии, выполним линейную регрессию и экстраполируем прецессию Меркурия.
Код
const perihelion = 0.307499AU # m
const aphelion = 0.466697AU # m
const maxVel = 58.98e3 # m/s
const minVel = 38.86e3 # m/s
const l1 = aphelion*minVel
const l2 = perihelion*maxVel
A = 4*π^2
l = (l1 + l2)/2
B = 3*l^2 / (c*AU)^2 # 1.0979084569263238e-8
function getCoord(z0, h, a, b)
z = z0
rhotemp = 0
rho2 = z0[1]^2 + z0[2]^2
steps = 0
# When the distance to the origin do not increase,
# we are at the maximum (aphelion).
while rho2 > rhotemp && steps < 1e9
rhotemp = rho2
z = rk4step(RHS, z, h, a, b)
rho2 = z[1]^2 + z[2]^2
steps += 1
end
return z[1], z[2], steps
end
Z0 = [0, -perihelion/AU, maxVel*T/AU, 0] # Initial condition
getPrecession(X, Y) = -atan(X/Y)
"""Return the precession (half period) in radians."""
r2aspc(radians) = 100*2*radians*(180/π)*3600/0.240846
"""Converts radians to arcseconds per century for Mercury."""
B0 = 10 .^ range( log10(1e-4), log10(1e-3), length = 20 )
Tmax = 0.28 # yr
n = 1000000 # stepИтак, мы выбираем ряд значений В, чтобы потом оценить для них прецессию. Чтобы удостовериться, что диапазон подобран правильно, проверим, что при В = 0 прецессия отличается от оной при В > 0 на несколько порядков:
X, Y, steps = getCoord(Z0, Tmax/n, A, 0)
p0 = getPrecession(X, Y)
X, Y, steps = getCoord(Z0, Tmax/n, A, B0[end])
p1 = getPrecession(X, Y)
println("With precession: $(abs(p1))")
println("Without precession: $(abs(p0))")
# With precession: 0.02328919368169773
# Without precession: 7.082451253461349e-6Чтобы найти наклон кривой, характеризующей изменение прецессии, воспользуемся пакетом Optim.jl
using Optim
phies(B) = begin X,Y,steps=getCoord(Z0, Tmax/n, A, B);
getPrecession(X, Y) end
phi = [ phies(b) for b in B0 ];
f(a) = sum( (a[1]*B0-phi).^2 )
res = optimize(f, [1.0], LBFGS() )
P = Optim.minimizer(res)[1]
plot(B0, B0*P, label="Fit",ylabel="Precession, \phi [radians per half orbit]")
scatter!(B0, phi, label="Data points",
xlabel="GR correction constant, B", legend = :topleft)Найденный параметр P задает наклон прямой, и теперь мы можем оценить релятивистскую поправку для прецессии меркурия!
p = round(r2aspc(B*P), digits = 2)
print("Precession of Mercury = $p arcsec per century")
# Precession of Mercury = 43.57 arcsec per centuryОжидаемое значение 43 угловые секунды за век, так что очень неплохо. Для остальных планет поправки куда меньше, но их тоже удается воспроизвести, причем даже аналитически. Методики нахождения смещения перигелия смотрим в предложенных ранее книгах и в дополнительных источниках:
-
Two conserved angular momenta in Schwarzschild spacetime geodesics
-
The Precession of Mercury’s Perihelion, Owen Biesel
-
A primer to numerical simulations: The perihelion motion of Mercury
-
Computational physics examples as IPython Notebooks
Теорию опробовали на иных космических телах в центре нашей галактики и за ее пределами, так что любой желающий может найти в открытом доступе наблюдаемые данные, выбрать аналитику или численные методы себе на вкус и удостовериться в эффективности теории относительности.
P.S. На всякий случай добавим ссылочки — если вдруг кому очень захочется всех заверить в никчемности релятивизма, то ему следует по пунктам разобрать каждый эксперимент, указать ошибки и предложить способ решить их.
-
https://en.wikipedia.org/wiki/Tests_of_special_relativity
-
https://en.wikipedia.org/wiki/Tests_of_general_relativity
-
What is the experimental basis of Special Relativity?
-
Experimental Tests of General Relativity
В любом случае, все эти теории подвергаются действию естественного отбора, так что хорошим тоном будет воздержание от подъема агрессивного бурления в комментах.
Орбита Меркурия
Орбита Меркурия является одной из самых эксцентричных среди из всех планетных орбит в Солнечной системе. Меркурий имеет орбитальный период 87,969 земных суток. В перигелии планета подходит к Солнцу на 46 млн. км, а в афелии удаляется от него на 69,8 млн км, разница в 23,8 млн км и дает эксцентриситет 0,21.
Орбита планеты
Она наклонена на 7 градусов к плоскости эклиптики Земли. Его можно увидеть пересекающим поверхность Солнца, только когда планета пересекает плоскость эклиптики и находится между Солнцем и Землей. Это происходит примерно раз в семь лет.
Хотя астрономы давно знали период обращения, они существено ошибались насчет его вращения.
До 1960-х годов считалось, что он приливно заблокирован Солнцем и всегда повернут к нему одной стороной и той же стороной.
Это происходило потому, что когда он был в положении для наблюдения, то был повернут к нам одной и той же стороной. В 1965 году, ученые астрономы, с помощью самого большого радиотелескопа в обсерватории Аресибо, установили, что период вращения планеты составляет около 115,8 дней. Существует прямая корреляция между орбитальным периодом и периодом вращения. Это называется орбитальным резонансом. На каждые 2 витка Меркурия вокруг Солнца, она вращается три раза вокруг своей оси, т.е. находятся в орбитальном резонансе 2:3 с Солнцем.
Несмотря на медленное вращение, он имеет глобальное магнитное поле. Два космических аппарата Маринер-10 и MESSENGER показали, что прочность и форма магнитного поля являются стабильными.
Магнитное поле
Оно дипольное и порождается динамо-эффектами в ядре. Эти динамо-эффекты, появляются от циркуляции в богатом железом жидком ядре планеты. Магнитное поле Меркурия отклоняется солнечным ветром и создает магнитосферу. Магнитосфера достаточно сильна, для того, чтобы поймать плазму солнечного ветра, которая способствуют выветриванию поверхности. Космический аппарат Маринер-10 обнаружил такую низко-энергетическую плазму в магнитосфере на ночной стороне планеты.
Как вы увидели из этой статьи, ученые многое знают о орбите Меркурия, но есть вещи, которые ждут своего открытия. Маринер-10 передал огромное количество информации, но к сожалению неполную из-за пролетной траектории. Космический аппарат MESSENGER уже заполняет пробелы и радует нас новыми открытиями из этого удивительного мира.
| Планеты Солнечной системы | |
|---|---|
| Карликовые планеты | Плутон· Церера· Хаумеа· Макемаке· Эрида |
| Планеты Земной группы |
Меркурий· Венера· Земля· Марс |
| Газовые гиганты | Юпитер· Сатурн· Уран· Нептун |
Меркурий — планета крайностей. Будучи ближайшей к нашему Солнцу планетой, он испытывает чрезвычайно высокие температуры поверхности. Но из-за практически полного отсутствия атмосферы и очень медленного вращения вокруг своей оси, Меркурий балансирует между сильной жарой и холодом. Обращенная к Солнцу сторона испытывает длительные периоды дня, в то время как ночная сторона испытывает чрезвычайно длительные периоды ночи.
Близость к Солнцу также означает, что Меркурий довольно быстро совершает полный оборот по орбите вокруг звезды. Один меркурианский год составляет примерно 88 земных дня. По сути, год на Меркурии всего лишь в 1,5 раза длиннее суток, которые длятся 58,646 земных дня.
Характеристика орбиты Меркурия и орбитальный период

Меркурий вращается вокруг Солнца на среднем расстоянии 57 909 050 км, что составляет около 0,387 а.е. — или чуть более одной трети расстояния между Солнцем и Землей. Длина окружности орбиты Меркурия составляет 360 млн км (2,406 а.е.). Его орбита также имеет максимальный эксцентриситет (0,205) среди планет Солнечной системы. Поэтому расстояние между Меркурием и Солнцем варьируется от 46 001 009 км (0,307 а.е.) в ближайшей точке (перигелий) до 69 817 445 км (0,467 а.е.) в наиболее отдаленной (афелий).
Как и все планеты, Меркурий движется быстрее всего, когда он находится в перигелии, и медленнее в афелии. Из-за близости к Солнцу, его средняя орбитальная скорость составляет 47,36 км/с — примерно 170 500 км/ч.
При такой орбитальной скорости Меркурию требуется 87,969 земных дня, или 0,241 земных года, чтобы совершить один оборот вокруг Солнца. Таким образом, можно сказать, что год на Меркурии длится почти как 3 месяца на Земле.
Сидерический и солнечный день
Раньше астрономы считали, что Меркурий приливно привязан к Солнцу и период его вращения вокруг оси совпадает с периодом обращения по орбите. Это означало бы, что одна и та же сторона всегда была направлена к Солнцу, тем самым гарантируя, что одна сторона была бы всегда солнечной (и чрезвычайно горячей), а другая испытывала постоянную ночь (и ледяной холод).
Однако улучшенные наблюдения и исследования планеты привели ученых к выводу, что на самом деле планета имеет медленный период вращения 58,646 дней. По сравнению с периодом обращения вокруг Солнца 87,969 дней, это означает, что у Меркурия есть спин-орбитальный резонанс 3:2. Простыми словами, планета совершает 3 полных оборота вокруг своей оси за каждые 2 оборота вокруг Солнца.

Другим следствием его спин-орбитального резонанса является значительная разница между временем, за которое планета совершает один полный оборот вокруг своей оси (звездные сутки), и временем, которое требуется Солнцу, чтобы снова появиться в том же месте на небе. (солнечные сутки). На Меркурии Солнцу требуется 176 дней, чтобы встать, зайти и вернуться в то же место на небе. Фактически это означает, что один солнечный день на Меркурии длится как два года!
Да, Меркурий — довольно экстремальное место. Температура на его поверхности колеблется от раскаленной до ледяной, а один солнечный день на планете длится столько же, сколько шесть месяцев на Земле. Добавьте к этому тот факт, что он практически не имеет атмосферы и подвергается воздействию чрезмерного количества радиации, и вы поймете, почему там не может существовать привычная нам жизнь.

Пришелец Инопланетянович
Если не оставишь коммент, то я приду за тобой!!!
Оставить коммент
Не нашли, то что искали? Используйте форму поиска по сайту
Содержание
- История изучения
- Расположение и размер планеты
- Строение
- Поверхность
- Орбита и движение
- Особенности атмосферы
- Магнитное поле
- Как найти Меркурий на небе
- Интересные факты
- Частые вопросы
- Видео-обзор научных фактов о планете Меркурий
История изучения
Точная дата обнаружения Меркурия неизвестна, поскольку планету описывали еще шумеры в 3000 году до нашей эры. Знали о планете также вавилонские и древнеегипетские жрецы, прекрасные астрономы древнего мира.
Название планеты идет от римлян, которые дали ей имя в честь античного бога Меркурия (в греческом варианте Гермеса), покровителя торговли, ремесел и посланца других олимпийских богов.
Также астрономы прошлого Меркурий порой поэтически называли утренней или вечерней зарей, по времени его появления на звездном небосводе.
Античные астрономы полагали, что Меркурий и его ближайшая соседка планета Венера вращаются вокруг Солнца, а не вокруг Земли. А вот Солнце уже в свою очередь вращается вокруг Земли
Точный возраст Меркурия неизвестен. Но он, вероятно, образовался примерно в тот же период, что и остальные планеты солнечной системы. На это указывают результаты радиоуглеродного анализа. На основе данных ученые установили, что Меркурий появился приблизительно 4,6 млрд лет назад.
Изучению планеты мешает близость расположения к Солнцу. Первые четкие фотографии планеты были получены в 1974 году, когда космический зонд «Маринер-10» осуществил 3 пролета над ней. Спустя более чем 40 лет до Меркурия добрался аппарат «Мессенджер», который тоже совершил облет планеты и через 7 лет он закрепился на ее орбите. Благодаря этому зонду ученые получили информацию о магнитном поле, атмосфере и особенностях рельефа планеты.
Меркурий в натуральном цвете, снимок пролёта «Маринера-10» в 1974/1975 годах.
Первые изображения Меркурия с высоким разрешением, полученные АМС «Мессенджер», 22 января 2008.
Первый обзор планеты в телескоп сделал в 17 веке Галилео Галилей. Но несовершенство его оптики не помогло получить сколько-нибудь существенных данных. Транзит планеты в 1631 году отметил Пьер Гассенди. Астроном Джованни Зупи заметил орбитальные фазы Меркурия. Случилось это в 1639 году и подтвердило вращение вокруг звезды и правильность гелиоцентрической модели.
Более точные сведения о планете представил в 1880 году Джованни Скиаперелли, который высчитал длительность орбитального пути Меркурия. В 1934 году Юджиос Антониади создал детально прорисованную карту поверхности планеты.
В 1962 году советские ученые смогли отбить первый радиолокационный сигнал Меркурия. А через 3 года американские астрономы повторили этот эксперимент и закрепили осевой оборот в 59 дней.
Но обычные оптические наблюдения не позволили рассмотреть особенности поверхности планеты. При этом с помощью интерферометров ученым удалось открыть физические и химические характеристики подповерхностных слоев.
Первые серьезные сведения о характеристиках поверхности Меркурия были получены только в начале 2000 годов. Сотрудники обсерватории Маунт-Вильсон составили большую часть карты планеты с помощью радиолокационного телескопа Аресибо с расширением 5 км.
Расположение и размер планеты
Меркурий – первая планета от Солнца. От небесного светила его отделяет 58 млн км. Вместе с Венерой, Землей и Марсом он составляет земную группу планет, которые объединяет некоторое сходство в размерах и строении.
Диаметр Меркурия примерно в 3 раза меньше земного и составляет 4879 км. По размерам данная планета уступает некоторым спутникам, которые встречаются в Солнечной системе.
Строение
Как и большинство планет солнечной системы, Меркурий состоит из 3 основных частей:
-
Строение Меркурия. Кора толщиной до 300 км. Состоит из реголита — сыпучего, рыхлого грунта. Твердая кора довольно тонкая – 100-200 километров по разным оценкам. По некоторым данным она может быть толщиной всего в несколько десятков километров. Она довольно хрупкая.
- Мантия толщиной до 600 км. Представляет собой переходную субстанцию из расплавленных составляющих ядра с одной стороны и застывшими слоями коры с другой.
- Ядро радиусом до 1800 км. Состоит из смеси железа и никеля. Ядро очень массивное по сравнению с другими планетами и составляет около 3⁄4 всего диаметра, что примерно равно размеру Луны.
Мнение эксперта
Цыпкин Трофим Петрович
Сотрудник обсерватории
Есть теорий, что образование Меркурия происходило из протопланетного диска, в котором легкие элементы были просто выметены солнечным ветром вглубь Солнечной системы. Из-за небольшого расстоянии от Солнца его влияние стоит брать в расчет. Вторая теория, что молодой Меркурий столкнулся с большой планетезималью и потерял часть своей коры, рассеявшейся в космосе. Это объясняет, почему ядро такое большое – потому что и планета изначально была вдвое больше.
Поверхность
Долгое время ученые не могли узнать, как выглядит поверхность Меркурия. Увидеть его можно только на закате или на восходе, и то недолго. И при этом он расположен очень низко над горизонтом, где самые плохие условия из-за толстой земной атмосферы. Так что в телескопы увидеть ничего не удавалось.
Все изменилось в 1974 году, когда около Меркурия трижды пролетел «Маринер-10». Он сфотографировал почти половину поверхности, и люди наконец-то получили возможность взглянуть на эту планету.
Сделанные Маринером показали снимки, что поверхность Меркурия сплошь покрыта кратерами. Как предполагают ученые, около миллиарда лет назад рельеф планеты был сформирован в виде равнин. Однако из-за отсутствия защитного атмосферного слоя поверхность Меркурия сильно пострадала от столкновений с космическими телами, которые оставили после себя многочисленные и достаточно глубокие воронки.
В 3D-модели Меркурия использованы текстуры с сайта НАСА, полученные зондом «Мессенджер». Не везде они хорошо стыкуются, но это лучшее, что есть на сегодняшний день.
На планете много кратеров, оставшихся после падения астероидов и мелких метеоритов. Но есть на поверхности и ровные долины, образованные текущей когда-то лавой. Это говорит о том, что ранее на планете была геологическая активность.
Поверхность напоминает лунную (снимок АМС «Мессенджер»)
Кратер Койпер (чуть ниже центра) (снимок АМС «Мессенджер»)
Еще одна характерная черта поверхности Меркурия – скалы, иногда растянувшиеся на тысячи километров. В высоту они бывают и 100 метров, и 2 километра.
Такое разнообразие верхнего слоя планеты на сегодняшний день не совсем понятно. Множество кратеров, накопившихся за миллиарды лет, говорит о том, что никакой активности планета Меркурий не проявляет. Однако лавовые поля говорят об обратном. Это противоречие пока ждет решения.
Ядро Меркурия постепенно сокращается – ученые считают, что за все время оно сократилось примерно на полтора километра. Это вызывает сжатие всей планеты, поэтому происходят подвижки тектонических плит. Кора выпячивается наружу, образуя скальные гряды.
При сжатии коры плиты наползали друг на друга, образуя выступы длиною в сотни километров. Образование такой «чешуи» должно было выглядеть катаклизмом немалого масштаба с сильными землетрясениями. Верхний край, наползающий на нижний, изгибался в виде волны, обрываясь с другой стороны глубокой пропастью. Такая местность типична для Меркурия.
Орбита и движение
У Меркурия крайне эксцентричная орбита. Он вращается в 46 млн. км от Солнца, на один оборот у него уходит 88 дней.
Орбита Меркурия овальной формы и сильно вытянута эпилептически, вследствие чего планета, то приближается к Солнцу на 47 миллионов километров, то отдаляется на 70 миллионов километров.
Если бы мы могли наблюдать Солнце с поверхности Меркурия, то оттуда оно выглядело бы в три раза больше, чем с Земли.
Экваториальная скорость вращения планеты составляет 10,892 км/час. Скорость движения вокруг Солнца, составляет 180 000 км в час. Один год на Меркурии равен 88 земным суткам.
Ось Меркурия отклонена от орбиты всего на 7 градусов. Данная особенность приводит к тому, что на планете не наблюдается смены времен года. По той же причине в районе полюсов есть зоны, на которые совсем не попадает солнечный свет.
Ученые установили, что Меркурий со временем постепенно смещается относительно Солнца. Данный эффект известен как прецессия. Смещение орбиты Меркурия по отношению Солнца было одной из неразрешимых загадок, с которой столкнулись астрономы в 19 веке. Чтобы объяснить данный эффект, ученые даже выдвинули предположение, что здесь располагается неизвестная планета, расположенная ближе к звезде.
Прецессия была объяснена только в 20 годах прошлого века. В это вредя Альберт Эйнштейн опубликовал свой труд «Общая теория относительности». Именно это позволяло понять, почему орбита Меркурия со временем смещается. Позднее данное предположение удалось подтвердить во время солнечного затмения.
Мнение эксперта
Цыпкин Трофим Петрович
Сотрудник обсерватории
Измерения показали, что спин-орбитальный резонанс Меркурия (количество оборотов, которое совершает планета на орбите) составляет 3:2. Из-за такой особенности возникает необычный эффект, который невозможно наблюдать на Земле. Если бы человек находился на поверхности Меркурия, то смог бы увидеть, как Солнце поднимается до максимальной точки на небосводе, затем по той же траектории опускается к горизонту.
Смена дня и ночи на Меркурии происходит крайне редко. Данный процесс занимает существенно больше времени, чем на других планетах Солнечной системы, поскольку он медленно вращается вокруг своей оси. Одно из полушарий планеты в течение продолжительного срока обращено в сторону Солнца. День и ночь на Меркурии длятся столько же, сколько и год
Особенности атмосферы
Для Меркурия характерна разреженная гелиевая атмосфера, в которой содержится малая концентрация неона, аргона и водорода. В основном они приносятся «солнечным ветром» и им же выбиваются.
Атомы газов находятся на огромных расстояниях друг от друга и не способны вступать в устойчивые связи из-за слабого магнитного поля планеты. Как следствие, выраженной атмосферы на Меркурии нет.
По этой причине температура на поверхности Меркурия очень сильно колеблется — гораздо сильнее, чем на любой другой планете Солнечной системы.
В экваториальных областях дневная температура составляет в среднем +427 градусов Цельсия, а ночью опускается до −173 градусов. Полярные регионы погружены в постоянный холод: температура здесь не поднимается выше −93 градуса.
Проведенные исследования показывают, что тонкий слой над поверхностью планеты состоит из кислорода (42%), натрия (29%), водорода (22%), гелия (6%) и калия (0,5%).
Магнитное поле
Согласно проведенным расчетам, магнитное поле Меркурия появилось примерно 3,7-3,9 млрд лет назад. Оно характеризуется дипольной структурой и высокой симметричностью. Оно незначительно (всего на 10 градусов) отклоняется от оси вращения, что усложняет определение природы его появления. Считается, что образованию магнитного поля Меркурия способствует эффект динамо, который обусловлен тем же процессом, который наблюдается на Земле.
При этом напряженность магнитного поля Меркурия составляет примерно 300 нТл, что в 100 раз меньше земного. Но несмотря на сравнительно малую напряженность, магнитное поле Меркурия способно оказывать влияние на движение солнечного ветра. Из-за этого возникает так называемая магнитосфера, которая также отличается небольшими размерами.
Ученые считают, что магнитное поле сформировано из-за циркуляции веществ в жидком ядре планеты. Причем из-за близкого расположения Меркурия к Солнцу возникает очень сильный приливной эффект. Благодаря этому ядро планеты остается жидким, что необходимо для образования магнитного поля.
В 2003 году, после запуска на Меркурий спутника «Мессенджер», ученым стало известно, что из-за близкого расположения к Солнцу его ветер образует над поверхностью необычные эффекты. Солнечный ветер вызывает образование завихрений, которые представляют собой сплетенные узлы магнитного поля планеты. Они вытягиваются на расстояние в 800 км. Кроме того, были выявлены так называемые «окна», или зоны, появление которых обусловлено снижением напряженности поля
Как найти Меркурий на небе
Меркурий всегда виден яркой звездой. Фактически, он будет первой из звезд, которые можно обнаружить на ночном небе. Но чтобы увидеть Меркурий, необходим открытый, чистый и ясный горизонт, без светового загрязнения.
Чтобы увидеть эту планету, нужно смотреть на восток утром, до восхода, или на запад вечером, после захода Солнца. В первой половине дня Меркурий стоит искать в восточной части небе, но из-за очень близкого расстояния до Солнца, планета никогда не отходит далеко от светила.
Необходимо быстро сориентироваться, и начать его искать вскоре после захода или восхода Солнца. Важно запомнить, что планета всегда находится в пределах 28 градусов от светила.
В умеренных широтах северного полушария Меркурий можно обнаружить с января по апрель, для вечерних наблюдений, и с июля по октябрь — для утренних.
Для южного полушария эти сроки нужно поменять местами. Посмотрите примерно на десять градусов выше нашей звезды, за сорок пять минут до восхода. Меркурий будет яркой, белой точкой, хотя в вечернее время может выглядеть розовым.
Меркурий можно наблюдать невооруженным глазом, но гораздо интересней использовать небольшой телескоп. Планета видна как маленький диск размером от 5 до 15 угловых секунд в поперечнике. Диск показывает фазы, то есть виден в форме серпа, как Луна.
Общее наблюдение Меркурия в телескоп в целом не отличаются от наблюдений других планет, но требует отличного оборудования. Лучше использовать рефлектор. Увидеть фазы Меркурия можно в 80-мм телескоп с увеличением 100х.
Но разглядеть какие-то детали на поверхности, хотя бы пятна, гораздо труднее. Для этого надо иметь не только отличный телескоп, но и опыт. Лучше делать это с апертурой от 100 мм. Телескоп в 250 мм позволит потренироваться в поиске деталей не только по терминатору, но и по противоположной стороне.
Интересные факты
- На Меркурии есть самый настоящий лед, который скрывается в глубине кратеров. Он мог быть принесен на Меркурий кометами и метеоритами или даже образоваться из водяного пара, который вырывается из недр планеты.
- Кратер, названный Койпером, является самой яркой зоной на Меркурии. Длина этого участка достигает 60 км.
- Около 4 миллиардов лет назад огромный астероид врезался в Меркурий. Силу этого удара можно сравнить со взрывом триллиона мегатонных бомб. От этого на поверхности Меркурия остался гигантский кратер, величиной, сравнимой с современным штатом Техас. Астрономы назвали его кратер Бассейнс Калорис.
Мнение эксперта
Ловкачев Дмитрий
Астроном любитель
Интересной особенностью этой планеты, является уменьшение ее размеров. Само уменьшение как полагают ученые вызвано постепенным охлаждением планеты, которое происходит миллионы лет. Вследствие охлаждения происходит сминание его поверхности и образование лопастевидных скал.
Частые вопросы
Сколько времени займет полет до Меркурия?
Продолжительность полета от Земли до Меркурия зависит от характеристик аппарата. Свет преодолевает это расстояние за 4,3 минуты. Отправленный в 1974 году летательный аппарат «Маринер-10» достиг Меркурия за 147 дней. Спустя 40 лет орбиты планеты достиг другой искусственный спутник – «Мессенджер». Ему на это потребовалось 1260 дней.
Какого цвета небо на Меркурии?
Небо над Меркурием даже днем темное, потому что у планеты нет атмосферы, рассеивающей солнечный свет.
Почему у Меркурия нет колец, как у других планет?
Причина в близости этой планеты к Солнцу. Кольца других планет образуются из ледяных обломков, кусков астероидов и прочих небесных объектов, которые вблизи Меркурия попросту расплавляться жаркими солнечными ветрами.
Может ли на Меркурии зародиться жизнь?
Нет. Для зарождения жизни на Меркурии абсолютно неподходящие условия. Чтобы на планете появились организмы, способные воспроизводить себе подобных, необходимо соблюдение ряда условий. В частности, нужно, чтобы вода долго не замерзала и не испарялась. Но на Меркурии наблюдаются значительные колебания температур, из-за которых это невозможно.
Видео-обзор научных фактов о планете Меркурий
Удаленность Меркурия от Солнца
Содержание
- 1 Общие сведения о планете
- 2 Орбита Меркурия
- 3 Положение Меркурия в Солнечной системе
- 3.1 Расстояние до Солнца
- 3.2 Расстояние до Венеры
Расстояние от Солнца до Меркурия непостоянно. Оно существенно отличается в разных точках траектории планеты из-за вытянутости ее орбиты.
Меркурий обращается по своей орбите вокруг Солнца с периодом около 88 земных суток. Credit: rutlib4.com
Общие сведения о планете
Меркурий входит в число планетарных тел, которые можно увидеть на небе без использования астрономической техники. Дата открытия его неизвестна. Произошло оно задолго до начала нашей эры. Свое название космическое тело получило от имени бога торговли — самого быстрого божества древнеримского пантеона. Причина — быстрое движение Меркурия по небесной сфере.
Основные параметры планеты:
- средний диаметр — 4,88 тыс. км;
- окружность по экватору — 15, 33 тыс. км;
- средняя плотность — 5,43 г/см³;
- ускорение свободного падения — 3,7 м/с² (значение на экваторе);
- период обращения вокруг своей оси — 58,5 земных дней;
- наличие естественных спутников — нет.
Масса Меркурия — 33,33022⋅10²³ кг. Не менее 40% объема меркурианской тверди (по другим данным — до 80%) занято расплавленным железным ядром. Выше находится силикатная мантия толщиной 500-700 км. Поверхностная кора имеет толщину 100-300 км. Такое необычное строение планеты может объясняться тем, что в момент рождения она была существенно крупнее. Впоследствии осталось лишь ее главное тело, а внешние слои разрушились. Это могло случиться в результате столкновения с крупным объектом или под влиянием солнечного нагрева.
Меркурий — самая первая и самая маленькая планета Солнечной системы. Credit: naked-science.ru
Поверхность Меркурия сильно кратерирована. С момента своего появления (около 4,6 млрд лет назад) планета попала под бомбардировку астероидов и космического мусора. Отсутствие атмосферы позволяло космическим телам падать на меркурианскую поверхность и оставлять на ней характерные следы. Одновременно внутренняя тектоническая активность рождала равнины и горы.
Солнечное тепло не накапливается на Меркурии, как на других космических телах с атмосферой. Это стало причиной температурных колебаний от +427 °С на солнечной стороне до -173 °С на ночной.
Эту планету изучали только 2 космических аппарата — «Маринер-10» в 1974-1975 гг. и «Мессенджер» в 2011-2015 гг. В конце 2025 г. к ней приблизится запущенная в конце 2018 г. исследовательская станция «БепиКоломбо». Ожидается, что она проработает на меркурианской орбите как минимум 1 год и за это время успеет:
- изучить состав поверхности;
- дать оценку геологической истории космического тела;
- исследовать местное магнитное поле;
- составить подробные карты объекта.
«Мaринер-10» — американская автоматическая межпланетная станция. Credit: airandspace.si.edu
Орбита Меркурия
Планета движется вокруг Солнца по эллиптической траектории, преодолевая каждую секунду 47,4 км и совершая 1 полный оборот вокруг светила за 88 земных дней. Меркурианская орбита наклонена на 7° относительно плоскости эклиптики.
Положение Меркурия в Солнечной системе
Меркурий в силу своего положения имеет только одну планету-соседку — Венеру.
Расстояние до Солнца
Дистанция от Меркурия до Солнца (57,9 млн км) не является постоянной. Существенная вытянутость орбиты планеты уменьшает эту величину до 45,9 млн км в точке перигелия и увеличивает до 69,7 млн км в афелии.
Такая разница в показаниях удаленности объясняется сильной вытянутостью меркурианской орбиты. Ее эксцентриситет (коэффициент сжатости) равен 0,2. Среди планет нашей системы это наибольший показатель. Высокая орбитальная эксцентричность Меркурия позволяет наблюдать его только в моменты максимального удаления от Солнца, иначе он теряется на фоне светила.
Расстояние до Венеры
Когда эти 2 планеты подходят на минимальное расстояние друг к другу, интервал между их орбитами составляет 50,3 млн км. Это немногим больше, чем наименьшая дистанция между Землей и Венерой. В моменты наибольшего отдаления Меркурия от второй планеты Солнечной системы расстояние между ними равно 166 млн км.
Оценка статьи:

Загрузка…