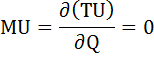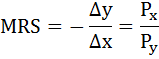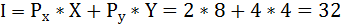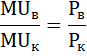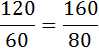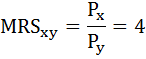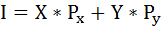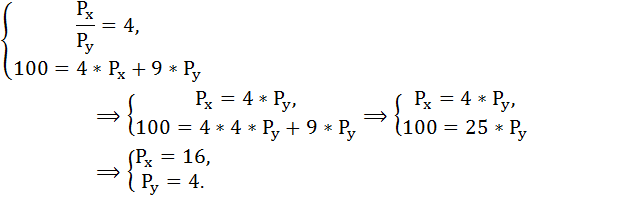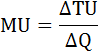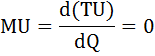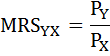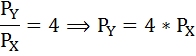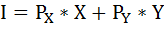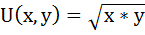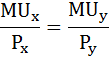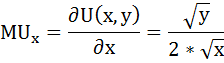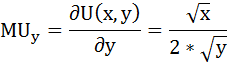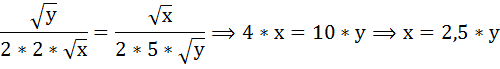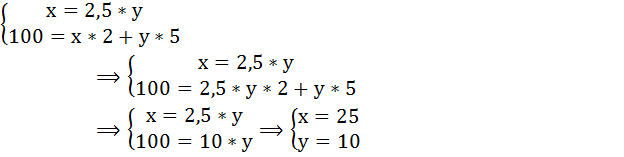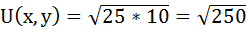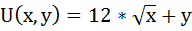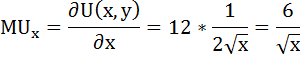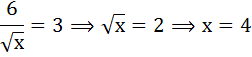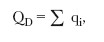Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q) = 1 – 2Q2;
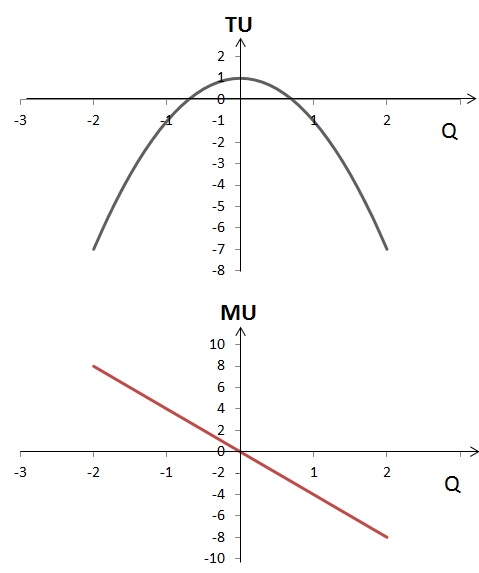
2) U(Q) = 5 + Q – Q2;
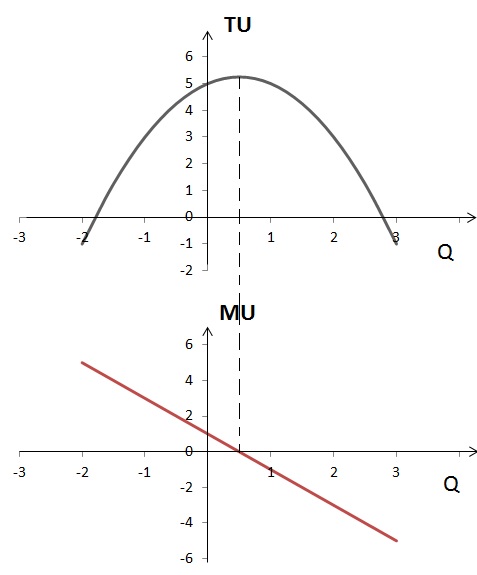
3) U(Q) = Q2 – Q3.
Как будут выглядеть функции предельной полезности?
Решение:
Функции предельной полезности определим с помощью первой производной от функции общей полезности.
1) MU(Q) = (1 – 2Q2)’ = – 4Q
2) MU(Q) = (5 + Q – Q2)’ = 1 – 2Q
3) MU(Q) = (Q2 – Q3)’ = 2Q – 3Q2
Общая полезность (TU) достигает своего максимума, когда предельная полезность (MU) равна нулю:
Таким образом, оптимальный для потребителя объем:
1) MU(Q)= – 4Q = 0, Q = 0
Изобразим функции общей и предельной полезности графически:
Как видно из графика, оптимальный для потребителя объем блага Q = 0. Общая полезность в этой точке максимальна.
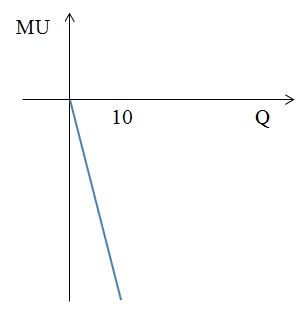
2) MU(Q) = 1 – 2Q = 0, Q = 1/2
Графически функции общей и предельной полезности для данного случая будут выглядеть следующим образом:
Как видно из графика, общая полезность максимальна при потреблении 1/2 единицы блага Q.
Внимательный читатель может возразить, что совсем необязательно было строить графики TU и MU с отрицательными значениями Q, так как значения функции при Q < 0 экономического смысла не имеют. Однако? как мы увидим далее, это окажется для нас полезным.
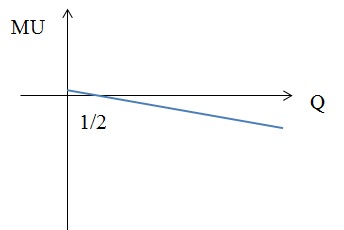
3) MU(Q) = 2Q – 3Q2
Приравнивая к нулю производную функции общей полезности получим квадратное уравнение:
2Q – 3Q2 = 0,
Корни этого уравнения:
Q = 0 и Q = 2/3.
Как видно из графика, максимум функции общей полезности находится лишь в точке Q = 2/3, который и будет оптимальным для потребителя.
Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
Запишем бюджетное ограничение:
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.
Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
2) U(Q)= 5 + Q – Q2
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
1) MU = –10 × Q = 0, следовательно, Q = 0;
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
Далее воспользуемся формулой бюджетного ограничения:
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
Аналогично находим предельную полезность товара y:
Далее воспользуемся бюджетным ограничением:
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
При х = 25 и у = 10 общая полезность достигнет максимума:
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
Оптимальный объём потребления будет достигнут при МU = P:
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
Вопрос 49
Общественные блага. Определение оптимального объема производства общественных благ.
ОТВЕТ
ОБЩЕСТВЕННЫЕ БЛАГА – блага, выгода от пользования которыми неразделимо распределена по всему обществу независимо от того, хотят или нет отдельные его представители приобретать это благо.
Общественные блага оплачиваются за счет общего налогообложения, а не покупаются отдельными потребителями на рынке. Примером общественного блага служит система национальной обороны, поскольку касается всех и каждого в равной степени.
Заметим, что кроме общественных благ существуют еще и общественные «антиблага» – общественные блага, равномерно налагающие издержки на группу людей. Это нежелательные побочные продукты производства или потребления: тепличный эффект, при котором сгорание полезных ископаемых угрожает глобальной переменой климата; загрязнение воздуха, воды и почвы отходами химической промышленности, производством энергии или использованием автомобилей; кислотные дожди; радиоактивные выбросы из-за испытаний ядерного оружия; истончение озонового слоя.
Различают чистые общественные блага и чистые частные блага.
Чистое общественное благо – благо, которое потребляется коллективно всеми людьми независимо от того, платят они за него или нет. Получение полезности от обеспечения чистым общественным благом единственным потребителем невозможно.
Чистое частное благо – благо, которое можно разделить среди людей так, что другим от этого не будет никакой выгоды или затрат.
Если эффективное обеспечение общественных благ часто требует государственных действий, то частные блага может эффективно распределить рынок.
Следовательно, чистое частное благо приносит полезность только покупателю.
Целый ряд благ не являются ни чисто общественными, ни чисто частными. Например, услуги полиции, с одной стороны, представляют собой общественное благо, а с другой – раскрывая кражи со взломом, они оказывает частную услугу конкретному лицу.
Чистые общественные блага имеют две основные особенности.
1. Чистые общественные блага обладают свойством неизбирательности в потреблении, означающим, что при данном объеме блага его потребление одним человеком не снижает доступности для других.
2. Потребление чистых общественных благ не обладает исключительностью в потреблении, т. е. не является исключительным правом. Это означает, что потребители, не желающие платить за такие блага, не могут быть лишены возможности их потребления. Чистое общественное благо невозможно выпускать «мелкими порциями», которые можно было бы распродать через кассовый автомат.
Кривая спроса на чистое общественное благо получается посредством сложения его индивидуальных предельных полезностей для всех потребителей при каждой возможной цене, что предполагает суммирование по вертикали индивидуальных кривых спроса.
Кривая спроса на чистое общественное благо, как и кривая спроса на чистое частное благо, имеет нисходящий наклон. Однако кривая спроса на чистое общественное благо отличается от кривой спроса на чистое частное благо двумя моментами. Первый – цена не является переменной величиной на вертикальной оси, поскольку нельзя назначить цену за отдельную единицу, ибо ее потребление не выступает исключительным правом. Второе отличие состоит в том, что в случае чистого частного блага люди корректируют объем спроса таким образом, чтобы приспособить его к своим вкусам и своему экономическому положению. Для чистого общественного блага это невозможно, поскольку на единицу этого блага не назначается цена. Все потребители должны потреблять объем производства целиком. Следовательно, при любом объеме предложения объем потребления такого блага каждым потребителем должен равняться объему предложения.
На рис. 49.1 и 49.2 изображены отличия между кривыми спроса на общественное и частное благо.
Рис. 49.1
Частное благо
Рис. 49.2
Общественное благо
Для чистого частного блага совокупный объем спроса при каждой возможной цене равен сумме индивидуальных объемов спроса:
где i = 1,…N.
Кривая спроса на чистое частное благо получается посредством сложения объемов спроса для каждой цены вдоль горизонтальной оси.
Кривая спроса на чистое общественное благо получается посредством сложения предельных полезностей для каждого объема вдоль вертикальной оси. Каждый из потребителей всегда потребляет одинаковые объемы блага.
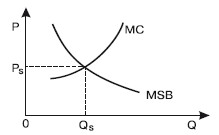
Определение оптимального объема производства общественных благ
Существует некоторый однозначно определяемый оптимальный объем общественного блага, обеспечивающий наибольшую эффективность использования ресурсов.
Оптимальный объем общественного блага может быть определен следующим образом:
MSB (Qs) = МС (Qs),
где MSB (Q,s) – предельная общественная выгода от потребления данного общественного блага в количестве: Qs; MC(Qs) – предельные издержки производства и обеспечения потребителей данными общественным благом в количестве Qs (рис. 49.3).
Рис. 49.3. Оптимальный объем общественного блага
Таким образом, для эффективного размещения благ в экономике данное общественное благо должно выпускаться в таком объеме, при котором предельная общественная полезность – выгода от потребления данного объема – равняется предельным общественным издержкам. Последние представляют собой стоимость ресурсов, необходимых для производства дополнительной единицы блага.
Выделяют перегружаемые и исключаемые общественные блага.
Целый ряд товаров и услуг по своим свойствам находятся между чистыми общественными и чистыми частными благами. Во многих случаях потребление блага неизбирательно лишь до определенного уровня потребления. Такие блага называют перегружаемыми общественными благами, которых может не хватить на всех потребителей. Начиная с определенного количества потребителей появление дополнительного потребителя приводит к уменьшению полезности, которую уже получали существующие пользователи.
В других случаях потребление благ неизбирательно, однако затраты на элиминацию дополнительных потребителей незначительны. Такие блага называются исключаемыми общественными благами, доступ к которым ограничен. Эти блага могут предлагаться фирмами, действующими с целью извлечения прибыли.
Примером перегружаемых благ может служить дорога. Дополнительные пользователи не сокращают доступность услуг шоссе, но уменьшается скорость движения существующих пользователей, что делает шоссе более опасным. Примером исключаемого блага может служить телевещание. Использование платежей и сборов за установку телевизоров помешает получению полезности теми, кто отказываются платить.
Исключаемые общественные блага – это такие блага, на которые легко назначить цену.
Чистые общественные блага, отличающиеся очень невысокой исключительностью, могут изготовляться и реализовываться в частном секторе посредством пакетирования (пакета) – объединения чистого общественного блага с другим благом, характеризующимся достаточным уровнем исключаемости, с целью участия всего пакета в операциях на рынке. Так, факт пакетирования был проиллюстрирован английским экономистом, лауреатом Нобелевской премии по экономике 1991 г. Рональдом Гарри Коузом на частном владении маяками в Англии в XVII–XIX вв. при сборе маячных пошлин в портах за портовые услуги судам.
Однако если уровень исключаемости общественных благ невысокий для их изготовления в частном секторе экономики, то они могут выпускаться в государственном секторе. В этом случае издержки производства возмещаются за счет налогов, что дает возможность решить проблемы «безбилетника» (неплательщика за выгоду одного экономического агента за счет другого агента). Выпуск благ в государственном секторе отнюдь не предполагает обеспечения экономически эффективного количества их производства, но вместе с тем – это более оптимальное средство удовлетворения ими покупателей.
Данный текст является ознакомительным фрагментом.
Читайте также
Вопрос 31 Монополистическая конкуренция: определение объема и цен.
Вопрос 31
Монополистическая конкуренция: определение объема и цен.
ОТВЕТМОНОПОЛИСТИЧЕСКАЯ КОНКУРЕНЦИЯ тип структуры рынка, состоящий из множества мелких фирм, выпускающих дифференцированную продукцию, и характеризующийся свободным входом на рынок и выходом с
ЛЕКЦИЯ № 4. Общественные блага в национальной экономике
ЛЕКЦИЯ № 4. Общественные блага в национальной экономике
1. Общественные блага: понятие, сущность, классификация
Общественные блага занимают в национальной экономике значительное место. Их адекватная интерпретация, управление их производством, распределением и
1. Общественные блага: понятие, сущность, классификация
1. Общественные блага: понятие, сущность, классификация
Общественные блага занимают в национальной экономике значительное место. Их адекватная интерпретация, управление их производством, распределением и потреблением являются залогом эффективного функционирования и
4. Теория оптимального объема выпуска продукции
4. Теория оптимального объема выпуска продукции
1. Определение оптимального объема производства и реализации продукции методом сопоставления валовых показателей.Предприятие, как правило, стремится получить максимальную прибыль.При прочих равных условиях наибольшее
10.4. Определение объема производства и цен в условиях монополистической конкуренции
10.4. Определение объема производства и цен в условиях монополистической конкуренции
Монополистическая конкуренция возникает там, где хозяйствуют десятки фирм, тайный сговор между которыми практически невозможен. Каждая фирма действует на свой страх и риск, сама
11.3.1. Определение объема спроса на фактор производства фирмой, являющейся совершенным конкурентом на рынке факторов и товаров
11.3.1. Определение объема спроса на фактор производства фирмой, являющейся совершенным конкурентом на рынке факторов и товаров
Конкурентный рынок факторов производства – это рынок, на котором имеется большое число продавцов и покупателей фактора производства, причем
11.3.2. Определение объема спроса на фактор производства фирмой, являющейся совершенным конкурентом на товарном рынке и монопсонистом – на факторном
11.3.2. Определение объема спроса на фактор производства фирмой, являющейся совершенным конкурентом на товарном рынке и монопсонистом – на факторном
Монопсония – рыночная структура, при которой множеству продавцов противостоит один, не имеющий потенциальных
11.3.3. Определение объема спроса на фактор производства фирмой, являющейся монополистом на товарном рынке и совершенным конкурентом на рынке факторов
11.3.3. Определение объема спроса на фактор производства фирмой, являющейся монополистом на товарном рынке и совершенным конкурентом на рынке факторов
Построение рыночной кривой спроса на труд со стороны предприятий, обладающих монопольной властью на товарном рынке, в
11.3.4. Определение объема спроса на фактор производства фирмой, являющейся монополистом на товарном и монопсонистом на факторном рынках
11.3.4. Определение объема спроса на фактор производства фирмой, являющейся монополистом на товарном и монопсонистом на факторном рынках
Когда фирма обладает и властью монопсонии на рынках рабочей силы и монопольной властью на рынках ее готовой продукции, работники
12.5. Общественные блага
12.5. Общественные блага
Еще одна ситуация, при которой рыночный механизм оказывается «несостоятельным», связана с так называемыми «общественными» благами. К их числу можно отнести национальную оборону, охрану общественного порядка, радио– и телепередачи, прогнозы
Занятие 15 Общественные блага
Занятие 15
Общественные блага
Семинар
Учебная лаборатория: отвечаем, обсуждаем и дискутируем…
Отвечаем:1. Чем отличаются чистые общественные блага от чистых частных благ?2. Почему чисто рыночные механизмы оказываются неэффективными в ситуациях с общественными
23. Общественные блага: понятие, сущность
23. Общественные блага: понятие, сущность
Общественные блага занимают в национальной экономике значительное место. Их адекватная интерпретация, управление их производством, распределением и потреблением являются залогом эффективного функционирования и развития
24. Классификация общественных благ
24. Классификация общественных благ
По характеру потребления выделяют следующие основные виды благ:1) общественные, отличающиеся тем, что находятся в свободном потреблении всеми членами общества и не могут быть использованы индивидуально;2) индивидуальные, отличающиеся
25. Виды общественных благ
25. Виды общественных благ
Основной особенностью общественных благ выступает граница, в рамках которой они потребляются. От этого зависит специфика производства, распределения и потребления благ.На основании территориальных границ, в рамках которых осуществляется
Вопрос 36 Обоснование объема производства и оценка эффективности ассортиментных программ
Вопрос 36
Обоснование объема производства и оценка эффективности ассортиментных программ
Анализ эффективности ассортиментных программ проводится по показателям: уровень выполнения плана по ассортименту, коэффициент обновления ассортимента, процент снижения
Оптимальный объем общественного блага [c.307]
ОПТИМАЛЬНЫЙ ОБЪЕМ ОБЩЕСТВЕННОГО БЛАГА — показатель, обеспечивающий максимально возможную эффективность ресурсного использования его можно рассчитать следующим образом [c.433]
Кривая спроса на объем этого общественного блага в простейшем случае выстраивается в итоге вертикального сложения двух кривых индивидуального спроса, при этом цена, которую данное общество готово выплатить за данный объем, формируется из суммы индивидуальных цен потребителей. С целью достижения эффективного применения ресурсов производство общественного блага должно осуществляться в объеме, при котором, опираясь на обычное правило принятия оптимальных экономических решений, размер предельной выгоды от потребления блага будет равен предельным издержкам производства данного блага. Следовательно, существует некий однозначно устанавливаемый оптимальный объем общественного блага, который обеспечивает наибольшую эффективность использования ресурсов. [c.630]
Оптимальный объем общественного блага 433, 630 [c.797]
Общество производит оптимальный объем общественного блага, если предельные издержки на его производство равны сумме, которую все люди в совокупности готовы платить за это благо. Кривые спроса на общественное благо должны суммироваться по вертикали, поскольку потребление блага одним человеком не приводит к уменьшению его потребления другими. [c.394]
Пусть х — Парето-оптимальный объем общественного блага, и срг(ж) =v,l(x)- 81(х)рх. [c.444]
Таким образом, в этой экономике Парето-оптимальные состояния характеризуются объемом производства общественного блага, максимизирующим благосостояние, х. Этот объем естественно назвать Парето-оптимальным объемом общественного блага. Если предельные полезности г> (ж) неотрицательны и не возрастают, причем хотя бы у одного потребителя они убывают, а предельные издержки с (у) положительны и не убывают, то такой объем будет единственным. [c.402]
Заметим попутно, что f = x2 — это как раз издержки производства общественного блага. Таким образом, оптимальный объем общественных расходов составляет величину [c.413]
Сравним оптимальное количество общественного блага и его объем в равновесии при голосовании с долевым участием. [c.430]
ОПТИМАЛЬНЫЙ ОБЪЕМ ПРОИЗВОДСТВА ОБЩЕСТВЕННОГО БЛАГА [c.203]
Определим, хотя бы только теоретически, оптимальный объем производства общественного блага. Для примера рассмотрим уличное освещение. Оно является общественным благом. Действительно, если данная улица освещена, то использование ее освещенности одним пешеходом не лишает такой возможности других. Кроме того, невозможно устроить так, чтобы для одних пешеходов свет горел, а для других нет. [c.203]
Оптимальный объем предоставления общественных благ частичное равновесие [c.401]
| Рис. 2. Оптимальный объем предоставления общественного блага. DA — линия опроса Антона DK — линия спроса потребителя Игоря DA+II — линия суммарного спроса 5 — линия предложения. | 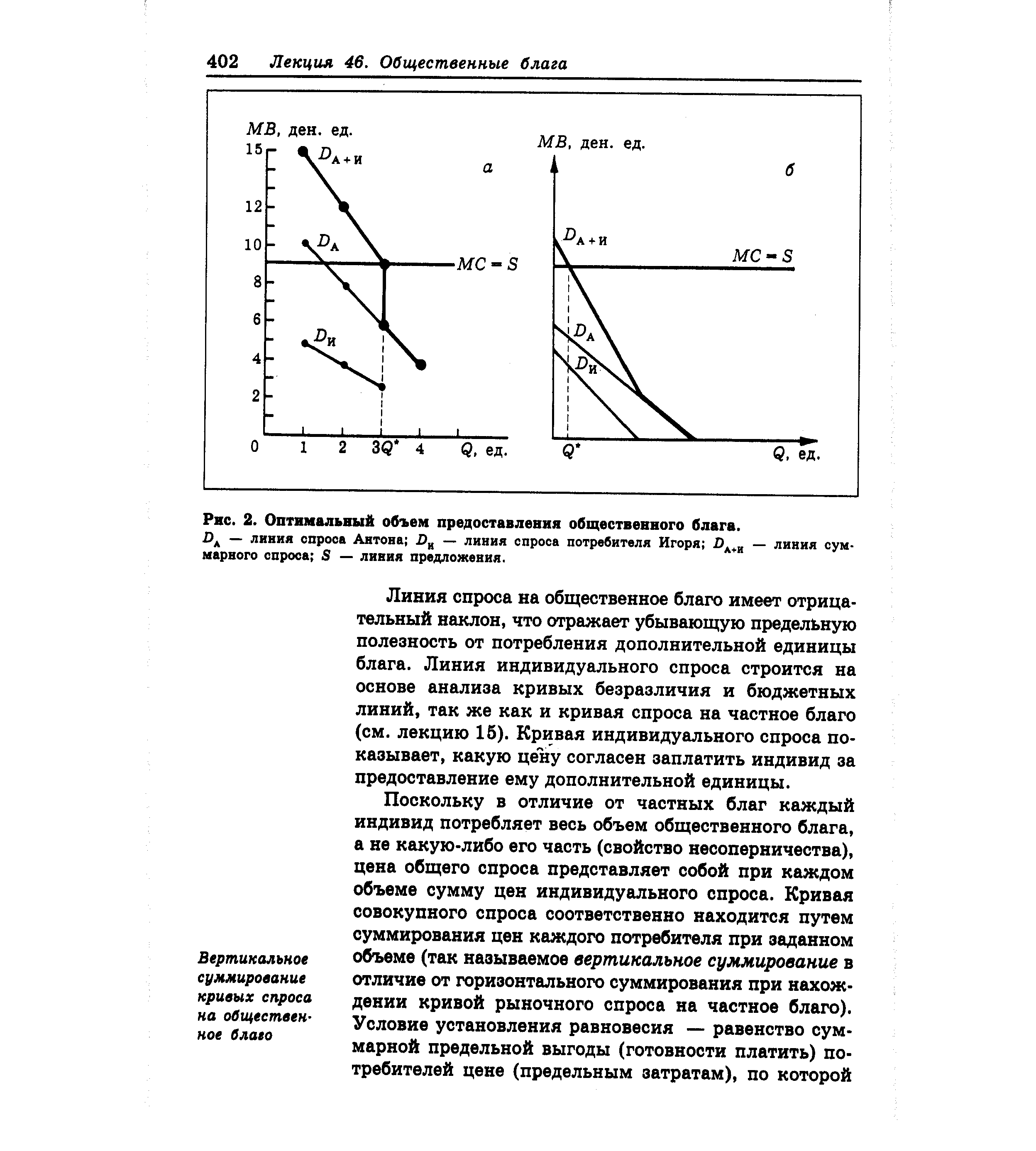 |
Проблема зайцев и оптимальный объем предоставления общественных благ [c.407]
Определяя оптимальный объем предоставления общественного блага в рамках моделей частичного и общего экономического равновесия, мы предполагали, что ничто не мешает выявлению истинных предпочтений потребителей и никто из них не ведет себя как заяц . На самом деле это, конечно же, не так, что немедленно сказывается на величине финансирования предоставления общественных благ. По этой причине такое большое значение придается стимулированию потребителей общественных благ к выявлению их истинных предпочтений. [c.407]
Определим, хотя бы только теоретически, оптимальный объем производства общественного блага. Для примера рассмотрим уличное освещение. Оно является общественным благом. Действительно, если данная улица освещена, то использование ее освещенности одним пешеходом не лишает такой же возможности других. Кроме того, невозможно устроить так, чтобы для одних пешеходов свет горел, а для других — нет. Допустим, что на данной улице проживают только два жителя Трифон и Федор. Они же являются единственными пользователями уличного освещения. На рис. 10а изображена кривая индивидуального спроса Федора на уличное освещение. По горизонтальной оси откладывается число уличных фонарей (Q). По вертикальной оси откладывается оплата Федором содержания одного уличного фонаря (Р ). Например, если бы содержание одного фонаря обходилось Федору в 20 руб. в год, то он был бы готов финансировать 2 уличных фонаря. В данном [c.167]
Предположим, на голосование поставлен вопрос об увеличении производства общественного блага сверх оптимального объема на 5 единиц. Какими будут итоги голосования Определите равновесный объем производства общественного блага в результате прямого голосования по принципу большинства. [c.193]
| Рис. 2. Оптимальный объем предоставления общественного блага. | 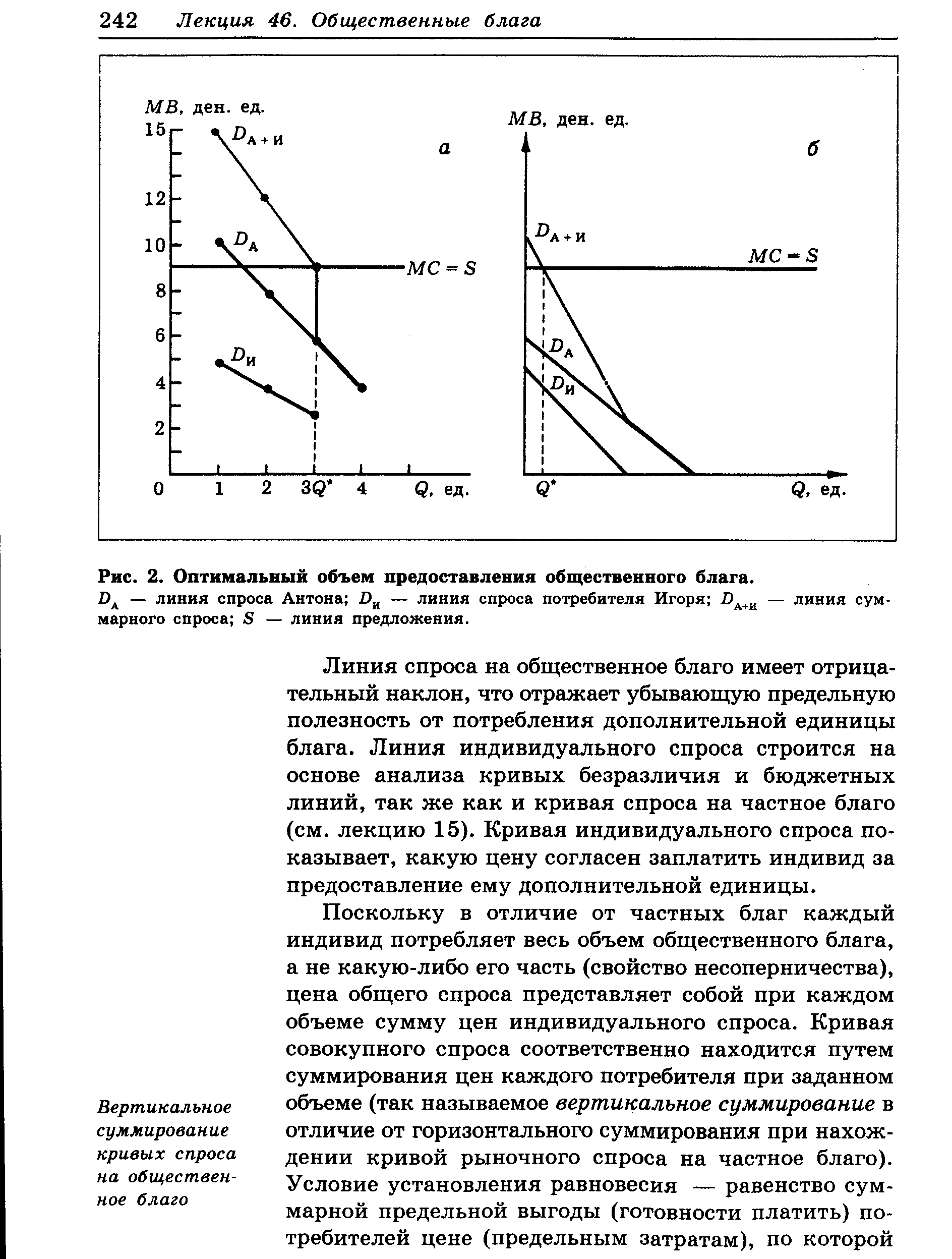 |
Мы рассматривали только случай частичного равновесия для чистого общественного блага. Как же в рамках анализа частичного равновесия будет найден оптимальный объем предоставления смешанного общественного блага [c.243]
С другой стороны, если какой-то участник хотел бы изменить объем производства общественного блага, но не может повлиять на исход голосования, то это не всегда признак того, что равновесие не оптимально. Для правил голосования VI, V2 и V3 неоптимальность обычно имеет место (в задачах мы ее докажем). Однако при «медианном» голосовании может быть, что ключевой (медианный) участник выберет такой объем производства общественного блага, который соответствует Парето-оптимуму (см. Пример (4.1) ниже). [c.39]
Оптимальный объем производства общественного блага составляет тогда величину у, удовлетворяющую соотношению Самуэльсона [c.413]
С другой стороны, оптимальный (по Парето) объем потребления общественного блага есть величина х, такая что [c.431]
Таким образом, объем производства общественного блага в равновесии при голосовании с равными долями финансирования xt является оптимальным тогда и только тогда, когда средняя предельная полезность для этого количества равна предельной полезности медианного потребителя. [c.431]
Поясним наши рассуждения следующим примером. Допустим, что национальная оборона финансируется группой неких частных лиц, стремящихся обезопасить только себя от внешнего врага. Однако созданная, например, система ПВО не может защищать только лиц, финансировавших это мероприятие. Она защищает всех граждан страны, включая и тех, кто ничего не платил ( безбилетников ) для создания оборонного потенциала. Проблема безбилетника не позволяет определить полный объем спроса и подрывает рыночные стимулы либо самого предоставления таких благ, либо их предоставления в общественно оптимальном объеме. [c.337]
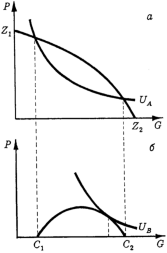
Для вывода условия парето-оптимальности зафиксируем полезность, получаемую индивидом А на уровне UA (рис. 4,а). Тогда при заданной кривой производственных возможностей 2 2 можно найти количество частного блага Р, доступного второму индивиду, В (по определению весь объем общественного блага доступен обоим индивидам, соперничества за его потребление не возникает). На рис. 4,6 граница набора потребительских возможностей индивида В обозначена С . Она получена как вертикальная разность между кривой производственных возможностей ZtZ2 и зафиксированной кривой безразличия потребителя А. [c.405]
Обозначим Kpriv множество частных благ, а Криъ — множество общественных благ. Для простоты предположим, что каждое общественное благо потребляется только потребителями, а предприятия могут общественные блага только производить. Поскольку мы не различаем доступное для потребления и потребляемое, то можно считать, что в потребительские функции прямо входит общий имеющийся объем общественного блага х = j г/j (k e Криъ) (начальные запасы общественных благ будем считать нулевыми). Итак, рассматриваемая нами экономика описывается следующей оптимизационной задачей получения Парето-оптимальной точки (х,у) [c.32]
В условиях, когда финансирование производства общественных благ является делом добровольным, объем их предоставления оказывается ниже оптимального. В первую очередь это связано с наличием так называемой проблемы безбилетника , суть которой состоит в следующем. Члены общества (или группы) могут оказаться склонны уклоняться от несения своей доли издержек, ожидая, что необходимые для производства общественного блага средства будут предоставлены другими. Таким образом, члены группы, придерживающиеся стратегии безбилетника , рассчитывают — благодаря свойству неисключительности общественных благ в потреблении — бесплатно воспользоваться плодами усилий своих коллег. В описанных условиях объем средств, направляемых на производство общественных благ, будет недостаточным для финансирования того объема благ, который обеспечивал бы максимальное удовлетворение потребностей группы в этих благах2. [c.690]
Баланс общественного продукта — баланс производства, распределения, потребления и накопления общественного продукта. Он характеризует воспроизводство общественного продукта, который представляет собой совокупность материальных благ, произведенных в отраслях материального производства, или, иными словами, это стоимость валовой» продукции отраслей материального производства (промышленности, сельского хозяйства, строительства, транспорта и др.), созданной в течепиз планового периода (год, пятилетне). Совокупный общественный продукт исчисляется как сумма валовой продукции отраслей материального производства за определенный период (год, пятилетне). Б. о. п. отражает объем и состав общественного продукта, его распределение и использование, показывает взаимосвязи отраслей, размеры расширенного воспроизводства, рост благосостояния народа. Совокупный общественный продукт классифицируется по экономическому назначению и использованию продукции на средства производства и предметы потребления по стоимости — на фонд возмещения и национальный доход. Кроме названных направлении, в Б. о. п. имеются показатели, характеризующие его по форме, — стоимостные и натуральные, по объему— общесоюзные, республиканские, территориальные и предприятий. Следовательно, Б. о. п. характеризует не только объемы совокупной массы материальных благ, но и важнейшие связи по их производству, распределению и потреблению. На его базе в плане устанавливаются оптимальные пропорции между всеми звеньями народного хозяйства отраслями, республиками, экономическими районами, сферами народного хозяйства. [c.16]
Иллюстративный характер доказательства тезиса о пропорциональности трудовых затрат и предельных полезностей воспроизводимых благ, предложенный Туган-Барановским, был в 1902 г. в работе экономиста киевской экономической школы (представителей которой, заметим, отличал большой интерес к использованию математики) Н.А. Столярова дополнен строгим алгебраическим доказательством. Столяров решал стандартную задачу нахождения условного кстремума, причем целевой функцией была функция общественной полезности или, как он писал, пользы, а ограничением — совокупный объем трудовых ресурсов. При условии, что общественная полезность любого блага зависит от количества только этого блага, частные производные целевой функции совпадают с предельной полезностью соответствующих благ, что и позволяет легко получить искомое соотношение. Эта небольшая работа оказалась по существу одной из первых математических работ в области общественной функции полезности и предвосхитила идею народнохозяйственного оптимума, которая в виде системы оптимального функционирования экономики (СОФЭ) активно разрабатывалась в нашей стране в 60-е юды. [c.393]
Рассмотрим функцию общественного благосостояния, обладающую свойством отделимости W=W(Vi(p,yi),…, Vn(p,yn)), где Vi(p,yi) — косвенные функции полезности отдельных индивидуумов. Сформулируем задачу поиска оптимальной шкалы акциза на благо х при фиксированных налоговых поступлениях следующим образом W(Vi,…,V )— max при условии R= fjXjq, где tj — ставка акциза нау -й товар, q — доналоговая цена, a Xj — объем спроса. Условия первого порядка в этом случае образуют следующую систему уравнений (верхний индекс у переменных в данном выражении соответствует номеру индивидуума) [c.105]
������ 46. ������������ �����
����������� ����� �������������� ������������ ����
� ������ ������� ���� ����� ����������� ������������� �������� ��������� ������� �� ������������ ���������, �. �. � �������� ����� �� ������ �� ��������� ��������� � ������������ ����������� — ��������������� ������������ �������� ��������� ������������ � �������������� ����.
���� �������� � ������������� �������. ����, ������� ����� �� ��������������, �� ����� ������������ ������ �� �������� ��������� ���������, �������� ������ �� �������� � ������������ ����������, ��������, ���, � ����� ������ ���� ������������ ���������, ������������ ���� ����� ������������� ������������. ���������� ����, ��� ����� � ����� ����� �� ������������ �����, �� �� ����������� ������������ ��� �� ��������� ���� ����� ����� ���� ��������, ���� ����� � ������� �� ��� ��� ���� ����������, �� ������� ����� ������� ����� �� ����. ����������� �����, ��� ��������� ��������� ������� � �������� ����� ��������� ����������. ������� ����� ����� �������������� ������ �� ������������ ����������� ����������, � ����� � ����� ���������� ���������� �� ����������. ��� ������ ����� ���������� �������� ���������� ������ ��� ���������, � ������ �� ����� ������ �� ������ �� ���������, �� � ��� �������. ������� ��� ������� ����� �� ��������� �� �������� ����� (������� ��������), ������� ����� �������� ������ �����������, ������������ ������ ���������. �� ���� ������� ������������ ����� ����� ������������� � ������� ������, ��� ��������� ��, � ������ ���� ��������� �����.
������ �� ��� ���� ����������� �� ��� ������? ������� ��� � ���, ��� ��� ������������ ���� ����� ����� ���� ��� «�����» (free rider). ���� ����� ������, ��� ����� � ����� ������ �������� �� ��������� �������, � ����� �� ������� ������ ������ ��������� ����� (��������������� ���������� �� ����������) �� ����� �������, ��� ������� ��������� ��� ����� �� ����� �, ����� ����, ������ �����, � �������������, ����� ������ ��������� ��� �����������. ������� ��, �������� «������» ��������� �� ������ ��-�� �������������� ��������� �������, �� � �� �������� ���������� � ��� ������ ���������� (�����������, ��������, ��� � ��� ����������, � ����� ������ ��� ����� ������ ������������ ������� � ������� �� �� ��� ������ ���������), ������� ������ �� ���� ����� �� ������ ��������� ������������ ����� � ��������� � ��������������� ���������������� � ���� ������ ������, ���������� ������� �������������� �������.
���� ������� �� �������������� ������������ ���� ����� �� ���� �����������, �� �������� ������� �� ������ �� �������������� �������������� ������������ ����������. ������ ������ ������ ��������������� � ��������� ������. ����� �� �� ���������������� �� ������� ������������� (��� ������������� �����������) �������� ������� �� ������ �������������� ������������ ���� � ����� ������������ ���� � ������� ������ �������������� ����������.
����������� ����� �������������� ������������ ���� : ��������� ����������
������ ���������� ���������� ������������ ����������� ������� ������ � ����������� � ���������� �����, � ������� ����� ������ ����� ����� ������ �����������.
������� ������ �� ������������ ����� ������������ ����� ����������� ���������� ��������� ���������� ������ (MB — marginal benefit) �� ������ ����������� �����. � ������ ������ ���������� ������ — ��� ���������� �������� �� ����������� �������������� ������� ������������� �����, ���������� � �������� ��������. ���������� ������ �������� ���������� �������� ������� �� ������ �������������� �������. ������ ������� ������, �� ������ ������������, ��� ������������ ��������, �. �. ��� ���������� �������, �������� ����� � ��� ���������. ����� �������, ���������, ��� �� ���� �� ������������ ������������� ����� �� ����� ���� ��� «����». ������� ������� �������������, �� ������������ � ������ �������� �����, ������ ������� ������ � ��������� ������� ��������. �� ���� ������� �� ����� �������� �������� ������������ �� ������������ �����.
����� ������ �� ������������ ����� ����� ������������� ������, ��� �������� ��������� ���������� ���������� �� ����������� �������������� ������� �����. ����� ��������������� ������ �������� �� ������ ������� ������ ����������� � ��������� �����, ��� �� ��� � ������ ������ �� ������� ����� (��. ������ 15). ������ ��������������� ������ ����������, ����� ���� �������� ��������� ������� �� �������������� ��� �������������� �������.
��������� � ������� �� ������� ���� ������ ������� ���������� ���� ����� ������������� �����, � �� �����-���� ��� ����� (�������� ���������������), ���� ������ ������ ������������ ����� ��� ������ ������ ����� ��� ��������������� ������. ������ ����������� ������ �������������� ��������� ����� ������������ ��� ������� ����������� ��� �������� ������ (��� ���������� ������������ ������������ � ������� �� ��������������� ������������ ��� ���������� ������ ��������� ������ �� ������� �����). ������� ������������ ���������� — ��������� ��������� ���������� ������ (���������� �������) ������������ ���� (���������� ��������), �� ������� ������ ���������� ������������� ����� ����� ���������� �������������.
�� ���. 2,� ��������� ����������� ����������� ����������� ������������ ������ �������������� ������������� ����� � ������ ���� ���������. ��������� ��� ������ � ������� ����������. �� ������ ������, ������������� �� �����, ����� ����� ��������� 10 ���. ��., � ����� — 5 ���. ��. �� ������ ������ ����� �� �������� 8 ���. ��., � ����� ������ 4 ���. ��., �� ������ �������������� 6 � 3 ���. ��. ��������� ������ ����� ��� �� �����, � ����� �������� �� �� ���� 4 ���. ��. ����� �������, ��� ���������� ������� �� ��������� ������� ������ ��������� � ����� 9 ���. ��.
���. 2. ����������� ����� �������������� ������������� �����.
DA — ����� ������ ������; D� — ����� ������ ����������� �����; DA+� — ����� ���������� ������; S — ����� �����������.
����� ������ �� ������������ ����� ����� ���� � ������������ (��� ������� �� ������� ��������� �����). ����������� ����, ��������, ��� ����� ����� ������������ ������� ���������� �������������� «������� ������ ���������» � ���������� ���������� (��. ���. 2,�).
��������, ��� ������������ � �������������� ������������ ���� ������� �� ������������� �������� ���������. �� ���� ������� ����� ����������� ������������ ����� ����� ���������� ������������ ������, ������ ����� ���������� ������� ������ ������������� � ������������� � ������������� ������� �������� ������������. ����� �������, �������� ������� ����������:

��� pi — ����, ������� ����� ��������� i — ��� �����������; MSC — ���������� ������������ �������; Q — ����� ������������� �����.
�� ������������� ������ ������ ���������� ���������� ��� ������� ������������� �����. ��� �� � ������ ������� ���������� ���������� ����� ������ ����������� ����� �������������� ���������� ������������� �����?
���� ������� ������� � ���������� ��� ������������� �����, ������� ����� ������� ��������, � ������� ��������, ������� �������� � ���������� ������������� � �����������. �� ���. 3,� ��������� ������ ��������������� ������ ������ � ����� �� ������� �������������� ����� (DA � D�) � ����� �� ��������������� ������������ ��������� ����� ����������� ������ (DA+�). �� ���. 3,� �� ���� ������ ���������� ������ �� �������� ������� (DEA � DE�) ����� ������������� ������������ �������� ����� ���������� ���������� ������ (DEA+�). � �������, �� ���. 2,� ���������� ����������� ����� ����������� ������ (DA+�) � ����� ���������� ���������� ������ (DEA+�), ������� ����� ������ �� ��������� ����� (D). ������� ������ ��������� � ���������� �������������� ������ �������������� ������� �����. �� ���� ������� ������������ ����� ����������� ������ � ����� ���������� ������ �� �������� ������� ������������ �����������. ����������� ����� ��� �������������� (Q*) ������������ ������ ����������� ����� ������ � ���������� ������.
���. 3. ����������� ������������ ������ �������������� ���������� �����.
����������� ����� �������������� ������������ ���� : ����� ����������
������ ������������ ���������� �������� � ��������� ��� ������� ���� ����� ���� (�������� � �������������) ���� ���������� �. ������������ � �������� 1950-� ��. � ������ ����������� ������������ ����������� ���������� �� ������������ (������ ����������� ��������), ���������� �������������� ���������� � ���������������� ������������ ��������� � ������������� ������������, � ����� ������� ����������� ������� ���������.
���������� ������� ����������� ������� �������� ������������ ���������� �������� ��� ������� ������������� �����.
�����������, ��� � ��������� ������������ ������ ��� ��������������� ����� — ������� (P) � ������������ (G). ������� ��� ����������� (A � B) �� ������ ��������� ����������, ������� ������������� ������ ����������� UA � UB. ������� ������������� ������������ �� ������� ������ ���������������� ������������ Z1Z2 (���. 4).
���. 4. ����� ������������ ������ ����������� ������������� �����.
��� ������ ������� ������-������������� ����������� ����������, ���������� ��������� A �� ������ UA (���. 4,�). ����� ��� �������� ������ ���������������� ������������ Z1Z2 ����� ����� ���������� �������� ����� P, ���������� ������� ��������, B (�� ����������� ���� ����� ������������� ����� �������� ����� ���������, ������������� �� ��� ����������� �� ���������). �� ���. 4,� ������� ������ ��������������� ������������ �������� B ���������� C1C2. ��� �������� ��� ������������ �������� ����� ������ ���������������� ������������ Z1Z2 � ��������������� ������ ����������� ����������� A.
����� ������, ����� Z1Z2 ���������� ��������� ������ �������� � ������������� �����, ������� ����� ���� ����������� ��� ������ ������������� ���� ��������� ��������; ������ UA �������� ��������� ������� ��� �� ����, ������� ����� ������� ����������� A ��� ������������� ������ ����������; ����� C1C2 (������� ����� Z1Z2 � UA) ����������, ��� �������� ����������� B, �. �. ����� ������ ���� ��� ��������.
���� ������������ ����������� B ������ ���������� ������ ����������� UB, �� ����������� ��� ���� ����� ����� E, ��� ��� ���������� ��������������� ��� �������� ��������������� ������������. ��������� ������ ��������������� ������������ C1C2 �������� ��� ������������ �������� ����� Z1Z2 � UA, �� � �� ������ ����� ����� �������� �������� ���� ������. � ���� ������� � ����� �������� E ������ ������ ����������� �������� B ����� ������� C1C2. ����� �������, ��������, ��� ���������� ����� ������ ����� ������� (P) � ������������ (G) ������ ��� �������� B �����

������ �������� ������� ������-�������� ��� ��������� � ������������ ������:

��� � ������ ��������� ������������

��� I — ����� ������������.
������ �� ����������� �������������, ����� ������� ������� �������� �� ������ ��� ������� ������������ ���� ������������.
����� ����� ���������� ������� ���� �����
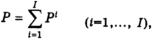
��� Pi — ���������� �����, ������������ i-��� ���������.
� ������ ������������ ����:
G = Gi (i = 1,…, I),
��� Gi — ���������� �����, ������������ i-��� ���������.
������������ ��������� ������ ��������� ����������:
�����������, ��� ����������� ������� ������������� � ������������, � ���������������� ����������� ��������� ����� ���� ������� ��������� ���������� ������ �������������:
�� ���� ������� (�������� ���������� ��������), ��������������� ����� ���������, ��������� ������� ����� �������, ������� �������� � ������������ ���������� ������� ����������� (����� ��� ����� ������� B, ��� � � ����������� ���� �������) ��� �������� ������ ���������� ���� ��������� ������������ � �������� ���������������� ������������ ���������. ������� ��������������� ��������� ��������:

��� ������� ���� ��������������� ������ �������� ������� ������� �������, �� ������� �������

|
(3) |
��� ��������, ������� ������� ������� ���������� ����� ����������, � ��� ���������� ���������� ����� ��������� ��������� ����� ������� ������� �������. ��� ���� ����� ������� ������� ������� ������������� �������� ����� ���������, ��������������� (3), ��������� ������������ ���������� ������� ���������� (1) � ���������� ��������� ���������������� ������������.
�������� «������» � ����������� ����� �������������� ������������ ����
��������� ����������� ����� �������������� ������������� ����� � ������ ������� ���������� � ������ �������������� ����������, �� ������������, ��� ����� �� ������ ��������� �������� ������������ ������������ � ����� �� ��� �� ����� ���� ��� «����». �� ����� ���� ���, ������� ��, �� ���, ��� ���������� ����������� �� �������� �������������� �������������� ������������ ����. �� ���� ������� ����� ������� �������� ��������� �������������� ������������ ������������ ���� � ��������� �� �������� ������������.
����������� ���������� � ��������� �������� ������������ ������������� �� ������ ����� ������������ �������������� ��� ������� � ������������ ����. ���� ����� ������������ ������������ ���������, �� ������ �� ��� ����� �������� �� ���� �������� �����, ��� ����� ������� �������� ������������ ��������� � ��������� ����������� ������������ (�������� ������������ ������ �� ������� ����������� — ���������� � ���������� ��������� ��������������� ��������� ���������� �����). ����� ���� ���� �� ������������ �����, ����� ����� ������������ ������������ �������� ��������� ����� ������������ ��������� ��������� — ������ ���������� ����� �������� � ����- ��� ���������������� �����. � ����� ����������� ��������� �������� ������������ ����� ������ ������������ ����� ������ ��� ������������� �����, ��� ��� ��������.
���� ������������ ��������� �����, ��� �� ���� �� ��� �� ����� �������� �� �������� ���� �������� ������, ������ ��� ������� ������ �������� ��� �������� ���� ������������. � ��������, ���� ����� ������������ �������� � ����� «���������» «������», ����������, ��� ������������ ����� ����� ������������� ��� ����������� �� �� ������.
� ������������� ������ ������� ����� ��� �������, � ������� �������� ������� ���������� �������� ��� ������� �������� «������». ����� �� ���� ���������� ������� ��������� � ����� ������ ���� ���������: ������������ ����� ������ ��������������� � ������-����������� ������, ��������� �������� ������������ ������ ���� � ��������� ����� ��������� �, �������, ������� �� �������������� ������������� ����� ������ ���� ����� ���������� �������� ��������� �� ��� ����.
�� ���������� ��� ������� — ������ ������� � �������� �������� ������ ������.
������ �������
� ������ ������� �������� �������������� � �������� �� �������������� ������������� ����� � � ���� ������� � ���� ��������. � �������� ���������� (��� � ���� ������� �������� ����������� �� �������) ���� ��������������� �� ����� �������, ��� ��� �������� ����������� ����� �� ���� � �� �� ���������� ������������� �����, ������� � �������� ����������� ������� ��� ��������������. ����, �� ����, ���� �� �������� �������� ��������� ���������, �� ���� ������� (��� ���������� ��������� ����), ������� ��, �� �������� ������ ��������� ����� — ��� ������������ ����� ���� �� ����� �������� ���������� ����� �� �������������� ������������� �����, ������� ������ ������ ��������� ��������.
���������� ���������� ������� ������ �������, ����� ������������ ����� ������������ ������ ����� ����������. ���� �������, ��� ��� ������� ������������ �� ������ ���� ���������, � ����� ������� � �������� ����� ��������: � �������� ������������� ���������� ��������� ��� ������������ ������, �������������� ��� ���������� ������ (��� ���������� ������ ���������). ����������� ������� ���������� ���������� �� ������� — ������ ���� ������ (���������) � �������� �����������.
�� ���. 5 �� ��� ������� (y) �������� ����� �������� ������������ ��������, �� ��� ������� — ���� �� ���� �����, ������� ������ ������� � � ������� �.
���. 5. ������ �������.
� ����� K ������� � �� ����� ������� ��������, 100 % ����������� ����� ������ ������� �. �� ���� �������� � ����� L ���� �������� � ������, � ������� � ���������� ������������ ������ ���������.
����������� �������� ���������� ���������� �� ����������� ������������� �����, �������� ������� ����� ������ � ������������� �������� DA ��� �������� � � DB ��� �������� �. ����� �, ����������� �� ����������� ���� ����� ������, ������������ ����� ���������� �� �������. ������ � ���� ����� ���������� �� ����������� ��������� ������� ������������� ����� ����� ��������� ���� ������������ ��� ���� ���������.
����� �� ��� ���������� ���������� � ����� ���� ���������� ��������� � ����� ����������? �������, �������������� ������������� ����� ������ ����� ���������� � ����� � �� ������������� ������������ � ������� ������������ ��������, � ������� ������������ ��������, ����� V. ����� ���� K� �� ����� ����� ��������, ������� � ��������� �� ����� ������� ������� ������������ ��������, � ������ Q, �� �� ���� �������� ��� ���������� ������������ ����� �� ���������� ������� �. ����� ������� ������� �������� ����� ���� ��������� ������ ��� �������� �������� ��������� ���� � � ��������� ���� �. �������, ��� �������� ����� ����������� ������ � ������� ���������� — ������� �������� V � ����� ������ ����� �������������� ��� ����� ���������, ��� ������� �������� ��������. � ���� ������ ���������� �� ������� ���������.
������ ������� ����������, ����� ������� ������������ ����� � ������� ��� (� ������������� ����� ��������� ���) �������� � �������� ������� �� ����������� ������ �������������� ������������� �����. ���� ������ ������� ������������ ��� �����������, � ���������� ������� ���������� ���������. ����� �� ��������� �������� ������������ ������� � �������, ��������� ������� � ����������� ���������� �� ����������� ��������.
������� ��, ������ ������� �� ������ �������� «������». � ������ ��������������, ���, ����������� � ������������ ��������� �������, ������� ������ ���� �������� ������������, �� �������� �������� «������» ��� ��� � ������� � ���, ��� ��� ����������� ����� ���� ������� ���������������� �������� � ����� �������������. ����� ����, ��� ������� ��������, ��� ���� ��� ���������� ����� ������� ����������� � ������ ���� ��������� � �������� ����������� ���������� ����� ������������� � ������� ������ � ������-�� �������.
������ ������� ���� ���������� � 1919 �., � �� �������� ��� ��������� �������������� ���� �������� ����� ��� ����� 40 ��� ����� ������������ ����� ������, ����� ���� ��������, ��� ���������� ������� �������� ����������� �� ������. � ����������� ������������ ���������� ������� ������ �� �� ���� ��� ������������ ��������� � ������������� �������, �������� ��������� � ����������������� ��������������, ����� ������ ���������� �������� ��� �������� ���������, � ������� ��� ������� �����������. � ��������� ������� ��������������, ��������, ��� � ������� ������ �������. � �� �� ����� ������ ������� ��� �� ����� ���� �������� ��� �������� �������� ������������ ������ � ��������� �������� �������, ������� �������������� �� �������.
����� ������
����� �� ��������� ��������, �������� «������» ��������� ���������� � ������������ ��������� �������� �������� �����������? ����� ������ ������������ ����� ������� ���������� ������ ���������.
���� ����� ������1 ��������������� ��� ������� �������� ��������� ������������ ������ ������������, �� ���������� ��� �������� �� ����� ������� � ��������� ������� � ����� ����������.
���������� ����, ��� ��� ������ ������-�� ������� ������ ������ � ������ ����� �������������� ���������� ��� ��������� (������� �� �� ������������� ����������). ������� �� ������� ������ ������, ������� �� ����� ��� �� ��������� �� ���������� ���� ��� ����� �������. �� ������ ����� «���������� �������» �������� ����� ����� ����������� ��� ���������� � ������������ �������� ������ ������. ����� ������ ��� ����������� ������ ����� ��������� �������������� ��������� �������, ������� ��������� ��, ���� �� ������ ������� �� �������� ������� � �����������. ������ ������ ������ ������ ������ ������ �����, ������ ��������� ������������� �����, �������� �� ����� �������. ���� ����� ����� �� ������� �� ��������� �������� � �� ���� ������� �� ������������ ��� ��� �������� � ����������� �������.
��������, ������ � ������ ������ ������� (�������� 1 � 2) ��������� �� ��������� ����������, � ���� ������ (����������) �� �� ������������� ��� ��������� �������������� � 10 � 15 ���. �. (��. �������). ���������� �� ������������� ��������� ��� ��� ����� ����, ��������� ������� ��� �� ����������. ��������, ������ ������ (������� 3) ��������� �� ������������� � ���������, ���� ������ �� ��� ������������� �� ������ � 20 ���. �., � ���������� ���������� ��� ���� � ���� ������� �������.
| ������� | ���������� | �������� | ����� ������ |
| 1 | 10 | 0 | 5 |
| 2 | 15 | 0 | 10 |
| 3 | 0 | 20 | 0 |
| ����� | 25 | 20 |
��������, ��� ����� ������� ������� � ������������� ����������. ����� ������ ��� �������� 1 ����� 5 ���. �. — ������ �� ��� ����� ���������� �� ���������� �������������� ���� ������ ���������� � ���������� ��� ��������� � �����������: ���� ������� 1 �� ��������, ����� ������� ������� � ������������� ���������. ��� �������� ������ �������� 3 �� 20 ���. �., �� ������������ � ������ ������, ������� ��� �� �������� ������ ���������� (������� 2) �� 15 ���. �., ��� ���� �������� ��������� �������������� � 5 ���. �.
����������� ������� ������ ����� ������ ��� ������� ������ ������� — �� ����� 10 ���. �. �������� ��������, ��� ������� ����� ��������� ������� �� ���������� ���������� � ��������������� �� ������ ������ ������������ ��� ������ ���� �������, �. �. ��������� �����������, ���� � ������ ������������� ������ ������, ��� ����� �������� �� ������� ����������. ��� �������� 3 ����� ������ ����� ����, ��������� ��� ����� �� ������ �� ����� ����������� � ����� ����� ��������������.
����� ������, ������ ����� ������ ������ �������� �������, ������������� ���������, ���������, ��� ���������� � ������ ��������� ���������� ����� ������������.
���� ������� 1 ������� ���� ������ ���������� �� ����������, ��������� ����������� � ����� ������ ����� �� ���������. ��������, ���� �� ����� ����� ���� ��� «����» � ������, ��� ���������� �� �������� ��� ������� ������, ����� ������� ���� ������������ — ������������� ���������. «����» ����� ������� ���, ��� � ����� �� ������� ������� ������ (���������� ��������� ��� ���� ����� ����), ������ ������, ������� ���� ��������� ���� ������ �� 10 ���. �.
���� ������� 3, ��������, ��� �� � �����������, ����� ������ � ����������� ����� ������� � ������� ������ ����� ������ �� ������������� ��������� �� 30 ���. �., �������� ������������� ����� ��������. �� ����� ������ ��� �������� ������ �������� 25 ���. �. (���������� ������ ������ ���� ���������), ��� ������, ��� ��� �������� ������ �� ������������� ��������� (20 ���. �.). ����� �������, ����� ������ ������ ���������� ����� � ��������� ������������ — ���� ��� ��������� ����� �� �������� �� ��������� ����������� � �������� ������, ���� �������� � �������� ������ «�������������» ����������.
����, �������� ��, �� �������� ����� �������������� ���� — ������ ������� ��������, ��� ��������� ��� �������� ������������ ����� �������� � ��������� ������� �� ��������� ������� ���������� � ��������� ������������� ������ ��������. �� ������ �� �� �������� «������»? �����, � ���������, ����� ������������� �� ������ ���� ������.
1. �������� � ���� ����������� ����� ����������� ��������, ��� ����� �������������� ��� ���� ������� ����������� ��������� �������� ������������. ����� ����, �� ��������� �� ������������� � ������� ���� ��������� ������� ������� � �����������. ������ ��� ������� �������� ����� ���������� ����� ��������� ������, ��� �� ������ ������ �� ������� � ����������� ������������ � ��������� �� ������� � ��� (��������, �� ��������� ��������� ���������� �� ������������� � �. �.), � ������ ��������� ���������� (����� �������� � ���������� �����������, ������� �������� �� ��� ����������, � ����� � «������������ ���������» ��. ������ 47).
2. �������������, ��� ������� ������������ ����������� ������� � ������������ ���� ����� ������������� ��� �����������, �� ����������� �� ��������.
3. ��� ������� ��������, ��� �������� ����� ������������ ����������� ��������� ����� ������, ���� �� ����� �� ��� ��������.
4. � �������, �������, ��� �������������, ��� � ������������, �������� ������ ������������� ������ ������. ���� ���� �������������� ��� ��������, ������� ������ �������� ��������� ������� �������� «������». ������ ���� �� ��� — ������������ ����� ������ ��������������� � ������-����������� ������ � ��������� �������� ������������ ������ ���� � ��������� ����� ��������� — ����� �������� ������ ������ ������������� (����, �������, �� ��������� �� �������� ��� ���������� ������). �� ����� ������ �� ����������� � ��������� ������������������ �������� �� ������������ ����� � ������� ��������� �������. ���������� ������� ����������� �� ���� ��������� ������, ������� ��������� �������������� ������������� �����, �������� �� ����� �������. ����� �� ������ ������ ������� ��������� ��������, ������ ��� «������» ������ ������ ������� ��������� — ��� ����� �������� � ��������� �� ���������.
�� ����������� ��� ��������� ��������� ������� �������� «������» — ������ ������� � ����� ������. � ��� � ������ ������ ������������ ����� ��������������� � ������-����������� ������. � �������� ���������� �� ������� ������ ������������� (������� �� �������������� ������������� ����� ����� ��������� ������ �� ��� ����), �� �������� �� ����� �������� � ��������� ����� �������� ������������. �������� �������� ������ ������ ������ �������� ��������������, �� �������� � ����������� ���������� ���������. ��� � ��������� ������ �������, ��� ������������ ������ ������ ����� ���� ��������� � ����� ������ ������������ ����������.
����, �� ��������, ��� ������� �������� «������» � ������ ������������ ������� �� ����������. � ��� �� �� ��������? ��� �� �������, �� ������ � ���� ������. �������������� ������������� «����������» �� «������» �������� ��� � ������ � ������������� ������������� ����������� � �������������� � �������������� ������������ ����. �������������� �������� ��������������� ����� ���� �������� ������� ��������� �� ����������� ������������� �����, ������� ��� �� ����� �� �������� ��� ���������� ���������������� �������������.
����� �� ������, ��� �� ���� �� ������� �� ���������� ��������, ���������� ������������ ���� ���������. ������ «����������» �� «������», � ���������, ����������.