Как найти оптимальные смешанные стратегии игроков

Наличие
у игры седловой точки вынуждает обоих
игроков обязательно реализовывать
только одну из чистых стратегий. Но, как
уже отмечалось выше, далеко не каждая
игра ее имеет. В таком случае невозможно
дать какие-либо содержательные
рекомендации по такому вопросу, как
следует поступать участникам однократно
проводимой игры. Однако принципиально
отличной является ситуация, когда игра
становится многократно
повторяющимся процессом. Появляется
возможность реализовать принцип
рандомизации,
т.е. внести в процесс выбора элемент
случайности или фактор вероятности. В
таких условиях применяется принцип
смешанных
стратегий.
Рассмотрим его на следующем примере.

Предположим,
имеется игра, заданная матрицей:

.

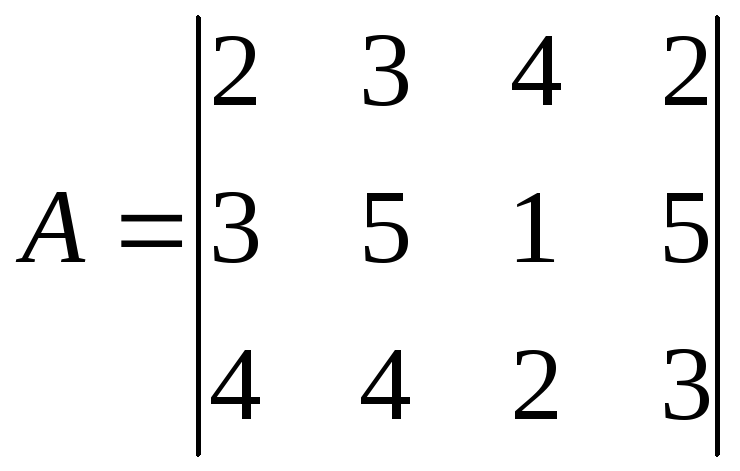
Для
нее α_max=2,
β_min=4,
т.е. игра не имеет седловой точки.
Предположим, что игроки сыграли 10 игровых
циклов, причем игрок А использовал за
этот период чистые стратегии: первую —
3 раза, вторую — 5 раз, третью -2 раза. Второй
игрок В за этот же период использовал
свои чистые стратегии: первую – 2 раза,
вторую -3 раза, третью – 1 раз, четвертую
– 4 раза. В таком случае говорят, что
игроки использовали смешанные стратегии,
которые записываются в виде вектор-строки
(в принятых обозначениях):

смешанная
стратегия первого игрока — ,

смешанная
стратегия второго игрока — .

Смешанной
стратегией игрока (например, А )в игре
с матрицей называется
упорядоченный набор действительных
чисел u_i
(i=1…m),
удовлетворяющих условиям

u_i
> 0,
.

Числа,
составляющие вектор-строку смешанной
стратегии, интерпретируются как
относительные частоты или вероятности
применения игроком соответствующей
чистой стратегии. Аналогично для игрока
В смешанная стратегия будет записана
так:

z_j
> 0,
j=1…n,
.

К
поиску решения игры в смешанных
стратегиях, так же как и при наличии
седловой точки, могут быть применены
критерии максимина-минимакса. В
соответствии с ними игрок А будет
выбирать свою смешанную стратегию таким
образом, чтобы максимизировать наименьший
средний выигрыш, а игрок В – минимизировать
свой максимальный проигрыш. Если u^*
— оптимальная смешанная стратегия
первого игрока, а z^*
— оптимальная
смешанная стратегия второго игрока, то
число

(26)

является
ценой игры.
С точки зрения математической статистики,
это средневзвешенное (или, точнее,
математическое ожидание) матрицы игры
за все игровые циклы.

Т
е о р е м а 1. Для
любой матричной игры в смешанных
стратегиях действительно соотношение:

,

т.е.
цена игры не
менее максимина, но и не более минимакса.

Определение
оптимальных стратегий и цены игры и
составляет сущность процесса нахождения
решения игры.

З а д а ч а 16.
Рассчитать цену игры, заданную матрицей

,

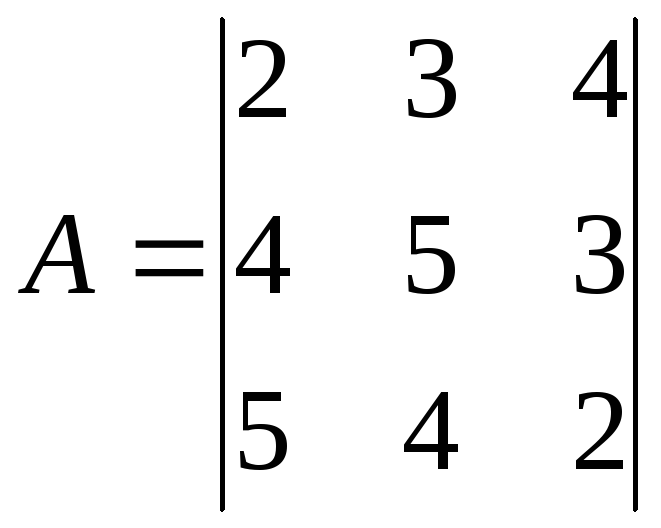
из
предположения, что игроки имеют
оптимальные смешанные стратегии u^*=(0,3;
0,3; 0,4), z^*=(
0,2; 0,5; 0,3).

Р
е ш е н и е . Определим максимин и минимакс
игры. Для этого выпишем вектор-строку
минимальных выигрышей игрока А и
максимальных проигрышей игрока В: α=(2;
3; 2), β=(5; 5; 4).
Тогда максимин равен
α_max
=3, минимакс
равен β_min=4.
Следовательно, цена игры будет находиться
между числами 3 и 4. Рассчитаем ее,
воспользовавшись выражением ( 26 ).

.

Получили
ответ – цена игры равна 3,63, что
соответствует теоретическим представлениям.

Справедлива
фундаментальная теорема Дж.Неймана,
которую приведем без доказательства.

Т
е о р е м а 2 (основная теорема матричных
игр). Любая
матричная игра имеет решение в смешанных
стратегиях.

Значение
и нетривиальность теоремы обусловлены
тем, что в общем случае матричные игры
в чистых стратегиях решения не имеют.

Т
е о р е м а 3. Для
того, чтобы число v
было ценой игры, а u^*
и z^*
—
оптимальными стратегиями, необходимо
и достаточно выполнение неравенства:

;
(j=1…n);

;
(i=1…m).

Эта
теорема определяет, что, соблюдая
оптимальные смешанные стратегии, первый
игрок может выиграть не менее цены игры,
а второй игрок имеет шанс проиграть не
более цены игры.

Т
е о р е м а 4. Если
один из игроков применяет оптимальную
смешанную стратегию, то его выигрыш
(или проигрыш второго) равен цене игры
v
независимо от того, с какими частотами
будет применять второй игрок стратегии,
вошедшие в оптимальную (в том числе и
чистые стратегии).

Она
важна тем, что позволяет выработать
методику решения игры для игр 2×2,
2×n,
m×2.

Рассмотрим
возможность приложения приведенных
выше теорем для решения парной игры
типа 2×2
аналитическим методом.

З а д а ч а 17. Найти
решение игры, заданной матрицей

.

Р
е ш е н и е. В данной задаче имеем две
стратегии первого игрока, т.е. m=2,
и две стратегии
второго игрока, т.е. n=2.
Прежде всего проверим, возможность
наличия седловой точки в данной игре.
Для этого выпишем минимальные выигрыши
первого игрока по двум чистым стратегиям
(по строкам) α=(2;
4) и максимальные
проигрыши второго игрока также по его
двум чистым стратегиям (по столбцам)
β=(6; 5).
Из этих векторов выпишем макcимин
для первого игрока α_max=4,
минимакс
для второго игрока β_min=5.
Так как они не равны, то решение следует
искать в смешанных стратегиях, а цена
игры должна быть в пределах
.

Предположим,
что для игрока А стратегия задается
вектором u=(u₁;
u₂),
а для игрока
В – вектором z=(z₁;
z₂).
Тогда, на
основании теоремы 4, при применении
игроком В чистой стратегии z₁
или z₂
игрок А получит средний выигрыш, равный
цене игры v
, т.е.

(при
стратегии z₁),

(при
стратегии z₂).

Помимо
двух записанных уравнений относительно
u₁^*
и u₂^*
добавим
уравнение, связывающее их как частоты:

.

Решая
полученную систему трех уравнений с
тремя неизвестными, находим

;

; .

Найдем
теперь оптимальную стратегию для игрока
В. В отношении его можно составить
следующую систему уравнений:

(при
стратегии u₁),

(при
стратегии u₂),

.

Здесь
имеются три уравнения, а неизвестных
два, т.е. одно из уравнений уже лишнее.
Решая систему, получаем

;
.

Следовательно,
решением задачи будут смешанные стратегии
при цене игры:

;
;
.

Результаты
полностью согласуются с теоретическими
предпосылками.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Если матричная игра содержит седловую точку, то ее решение находится по принципу минимакса. Если же платежная матрица не имеет седловых точек, то применение минимаксных стратегий каждым из игроков показывает, что игрок I обеспечит себе выигрыш не меньше a, а игрок II обеспечит себе проигрыш не больше b. Так как a < b, то игрок I стремится увеличить выигрыш, а игрок II уменьшить проигрыш. Если информация о действиях противной стороны будет отсутствовать, то игроки будут многократно применять чистые стратегии случайным образом с определенной вероятностью. Такая стратегия в теории игр называется смешанной стратегией. Смешанная стратегия игрока — это полный набор его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями. Для применения смешанных стратегий должны быть следующие условия:

1) в игре отсутствует седловая точка;

2) игроками используется случайная смесь чистых стратегий с соответствующими вероятностями;

3) игра многократно повторяется в одних и тех же условиях;

4) при каждом из ходов один игрок не информирован о выборе стратегии другим игроком;

5) допускается осреднение результатов игр.

Основная теорема теории игр Дж. фон Неймана: Любая парная конечная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно среди смешанных стратегий.

Отсюда следует, что каждая конечная игра имеет цену, которую обозначим через g, средний выигрыш, приходящийся на одну партию, удовлетворяющий условию a £ g £ b. Каждый игрок при многократном повторении игры, придерживаясь смешанных стратегий, получает более выгодный для себя результат. Оптимальное решение игры в смешанных стратегиях обладает следующим свойством: каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет оптимальную смешанную стратегию, так как это ему невыгодно.

Чистые стратегии игроков в их оптимальных смешанных стратегиях называются Активными.

Теорема об активных стратегиях. Применение оптимальной смешанной стратегии обеспечивает игроку максимальный средний выигрыш (или минимальный средний проигрыш), равный цене игры G, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий.

Смешанные стратегии игроков S1 и S2 обозначим соответственно A1 , A2 , … Am и B1 , B2 , B3 … Bn, а вероятности их использования через pA = (p1, p2, …, pm) и qB = (q1, q2, …, qn), где pi ³ 0, qj ³ 0, при этом .

Тогда смешанная стратегия игрока I — SI, состоящая из стратегий A1, A2, …, Am, имеет вид:

.

Соответственно для игрока II:

.

Зная матрицу А для игрока I можно определить средний выигрыш (математическое ожидание) :

,

Игрок I, применяя свои смешанные стратегии, стремится увеличить свой средний выигрыш, достигая

.

Игрок II добивается:

.

Обозначим через и векторы, соответствующие оптимальным смешанным стратегиям игроков I и II, при которых выполняется равенство:

.

При этом выполняется условие:

Решить игру — это означает найти цену игры и оптимальные стратегии.

Рассмотрим наиболее простой случай конечной игры 2 ´ 2 без седловой точки с матрицами:

,

С платежной матрицей

.

Требуется найти оптимальные смешанные стратегии игроков , и цену игры g.

Каковы бы ни были действия противника, выигрыш будет равен цене игры g. Это означает, что если игрок I придерживается своей оптимальной стратегии , то игроку II нет смысла отступать от своей оптимальной стратегии .

В игре 2 ´ 2, не имеющей седловой точки, обе стратегии являются активными.

Для игрока I имеем систему уравнений:

Для игрока II аналогично:

Если g ¹ 0 и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы не равен нулю, следовательно, эти системы имеют единственное решение.

Решая систему уравнений (10) и (11) находим оптимальные ешения, и g:

Пример: Дана платежная матрица:

Найти решение.

Решение. Так как a = 3, b = 5, то a ¹ b, то и матрица игра не имеет седловой точки. Следовательно, решение ищем в смешанных стратегиях. Запишем системы уравнений:

Для игрока I:

Для игрока II:

Решив эти системы находим:

Следовательно оптимальные стратегии игроков имеют вид:

,

Теория игр. Матричные игры. Онлайн калькулятор

С помощю этого онлайн калькулятора можно решить задачу теории игр. Для решения задачи теории игр задайте количество строк и количество столбцов матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Теория игр − теоретическая часть

Бывают ситуации, в которых сталкиваются интересы двух и более сторон. При этом эффективность принимаемого решения одной стороны зависит от действий другой стороны. Такие ситуации называются конфликтными. Конфликтная ситуация называется антагонистической, если увеличение выигрыша одной стороны на определенную величину приводит к уменьшению выигрыша другой стороны на такую же величину. Математическая модель таких ситуаций описывается матричной игрой. Участники игры (т.е. лица, принимающие решение) называются игроками. Принятие игроком того или иного решения в процессе игры и его реализация называется ходом. Ходы могут быть личными (т.е. сознательными) и случайными. Стратегия игрока − осознанный выбор одного из множества вариантов его действий. Стратегия называется чистой, если выбор игрока неизменен от партии к партии. У первого игрока есть m чистых стратегий, а у второго игрока n чистых стратегий. Если множество стратегий игроков конечный, то игра называется конечной, а если хотя бы у одного игрока множество стратегий бесконечно, то игра называется бесконечной. Стратегия игрока называется оптимальной, если она обеспечивает данному игроку (при многократном повторении) максимально возможный средний выигрыш или минимально возможный средний проигрыш.

Игры, в которых учавствуют 2 игрока, называются парными, а игры с большим числом участников − множественными. Если в парной игре выигрыш одной стороны точностью совпадает с проигрышем другой стороны, то игра называется игрой с нулевой суммой.

В зависимости от вида функций выигрышей, игры бывают матричные, биматричные, непрерывные, выпуклые и др.

Рассмотрим матричную игру двух участников с нулевой суммой и конечным числом возможных ходов.

Решение матричной игры в чистых стратегиях

Пусть игроки A и B распологают конечным числом возможных действий (чистых стратегий). Обозначим их через и , соответственно. Игрок A может выбрать чистую стратегию . В ответ на этот выбор, игрок B может выбрать чистую стратегию . Выбор стратегии первого игрока и ответный выбор стратегии игрока B единственным образом определяет результат a_ij выигрыш игрока A или проигрыш игрока B.

Таким образом игра с нулевой суммой однозначно определяется матрицей

которая называется платежной матрицей или матрицей выигрышей. Строки матрицы (1) определяют стратегии первого игрока (), а столбцы соответствуют стратегиям второго игрока ().

Игра проходит партиями. Партия начинается с первого игрока. Он выбирает некоторую строку i матрицы. В ответ на это второй игрок выбирает некоторый столбец j. На этом заканчивается партия и второй игрок платит первому сумму a_ij, если a_ij>0 или первый игрок платит сумму a_ij второму игроку, если a_ij<0. Цель каждого игрока − выиграть как можно большую (или проиграть как можно меньшую) сумму в результате большого числа партий.

Чтобы определить наилучшие стратегии игроков, мы предполагаем, что участники разумны, т.е. делают все, чтобы добится наилучшего результата для себя. Методом логических рассуждений найдем наилучшую стратегию игрока A. Для этого проанализируем по шагам все его стратегии. Выбирая стратегию A_i (строка i) игрок A должен рассчитывать, что игрок B должен ответить такой стратегией B_j (столбец j), чтобы выигрыш первого игрока был бы минимальным. Поэтому найдем для каждой строки минимальное число:

Зная для каждой строки число α_i (i=1,2,…m) игрок A должен выбрать ту стратегию, при котором его выигрыш будет максимальным:

Величина α называется минимальным гарантированным выигрышем, к которому может достигнуть игрок A, при любых стратегиях игрока B. α называется нижней ценой игры или максимином.

Рассмотрим, теперь, игру со стороны игрока B. Игрок B заинтересован уменьшить свой проигрыш (или минимизировать выигрыш игрока A. Поэтому для каждого столбца он оценивает свой максимальный проигрыш в связи с тем, какую стратегию i выберет игрок A:

Зная для каждого столбца число β_j (j=1,2,…n), игрок B должен выбирать ту стратегию, при котором его проигрыш будет минимальным:

Величину β называют верхней ценой игры или максимином, к которому может достигнуть игрок A, при любых стратегиях игрока B. α называется нижней ценой игры или максимином. Она показывает максимальный проигрыш, которого может достигать игрок B при любых стратегиях игрока A.

Теорема 1. В матричной игре нижняя цена игры не превосходит верхней цены, т.е. α ≤ β.

Действительно:

Если для чистых стратегий A_k и B_l игроков A и B имеет место равенство α = β, то пару чистых стратегий (A_k,B_l) называют седловой точкой матричной игры а γ=α = β чистой ценой игры. Элемент a_kl называют седловым элементом платежной матрицы.

Заметим, что отклонение игрока A от максимальной стратегии A_k ведет к уменьшению его выигрыша, а отклонение игрока B от минимальной стратегии B_l ведет к увеличению его проигрыша. Поэтому A_k и B_l являются оптимальными чистыми стратегиями игроков A и B, соответственно.

Тройку (A_k, B_l, γ) называют решением матричной игры. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.

Решение матричной игры в смешанных стратегиях

Если матричная игра не имеет седловой точки, то α ≠ β, и, Теорему 1, получим: α < β. Получается, что применение минимаксных стратегий приводит к тому, что выигрыш игрока A не больше α, а проигрыш игрока B не больше β. В этом случае решение матричных игр находят в смешанных стратегиях.

Смешанной стратегией игрока A называется вектор , где

p_i− вероятность, с которой игрок A выбирает свою чистую стратегию A_i.

Смешанной стратегией игрока B называется вектор , где

q_j− вероятность, с которой игрок B выбирает свою чистую стратегию B_j.

Замемим, что чистые стратегии являются частным случаем смешанных стратегий. Если, например игрок A выбрал чистую стратегию A₃, то это означает, что вероятность ее выбора равна 1, т.е. . Средняя величина выигрыша игрока A (или проигрыша игрока B) определяется по формуле математического ожидания:

Функция M(p,q) называется платежной функцией матричной игры с матрицей. Смешанные стратегии p^* и q^* называются оптимальными, если они образуют седловую точку для платежной функции M(p,q), т.е.

Значение платежной функции при оптимальных смешанных стратегиях p^* и q^* называют ценой игры:

Теорема 2 (Основная теорема теории матричных игр). В любой матричной игре у игроков есть оптимальные смешанные стратегии.

Доказательство. Пусть игра имеет платежную матрицу

где все элементы положительны.

Пусть и − смешанные стратегии игроков A и B , соотвестстенно.

Математическое ожидание выигрыша игрока A равна:

При любом выборе игроками своих смешанных стратегий p и q, математическое ожидание будет положительным, так как все элементы a_ij платежной матрицы положительны, p_i неотрицательные числа и среди них есть хотя бы одно положительное число, q_j неотрицательные числа и среди них есть хотя бы одно положительное число.

Нижняя цена игры

так как a_ij >0, i=1,2,…m, j=1,2,…n. Поскольку α>0 и γ не может быть меньше нижней цены игры, то γ ≥ α, а так как α>0, то γ >0.

Пусть игрок A выбирает такую стратегию p, что математическое ожидание его выигрыша независимо от того, какую стратегию выбирает игрок B было не меньше некоторой величины γ:

где p_i >0, i=1,2,…m, . Каждая строка в системе линейных неравенств (3) соотвесттвует определенной стратегии игрока B.

Преобразуем систему нерравенств (3), введя новые обозначения:

Разделим все неравенства системы (3) на положительное число γ. Тогда имеем:

y_i >0, i=1,2,…m.

При этом

Цель игрока A − максимизировать свой гарантированный выигрыш γ или минимизировать величину

Таким образом, приходим к следующей задаче линейного программирования:

Сделав аналогичные рассуждения с позиции игрока B, получим следующую задачу линейного программирования:

Покажем, что задачи линейного программирования (4) и (5) имеют допустимые решения. Так как a_ij >0, то можно подобрать достаточно большие положительные числа y_i, i=1,2,…m так, чтобы выполнялись неравенства (4b). Значит задача линейного программирования (4) имеет допустимое решение.

Допустимое решение задачи линейного программирования (5) является нулевой вектор. Таким образом, пары двойственных задач линейного программирования (4) и (5) имеют допустимые решения. Тогда, согласно теории двойственных задач линейного программирования, обе эти задачи имеют оптимальные планы , , при этом оптимальные значения целевых функций данных задач равны:

Цена игры равна:

Найдем оптимальные смешанные стратегии игроков:

Тогда

Пара образует седловую точку данной матричной игры в смешанных стратегиях.

Если в матрице есть отрицательные элементы или нули, то можно сделать матрицу положительным, добавив к каждому элементу матрицы достаточно большое положительное число r. Тогда получим следующую матрицу A’(a_ij+r).

Математическое ожидание выигрыша игрока A с платежной матрицей A(a_ij):

Математическое ожидание игрока A с платежной матрицей A’(a_ij+r):

Тогда

Игра с платежной матрицей A’ имеет седловую точку в смешанных стратегиях:

Следовательно, игра с платежной матрицей A также имеет седловую точку в смешанных стратегиях а цена игры с платежной матрицей A равна:

Для рассмотрения численного примера матричной игры, введите в калькуляторе в начале страницы элементы матрицы и нажмите на кнопку вычислить. Онлайн калькулятор выдаст подробное рашение задачи.