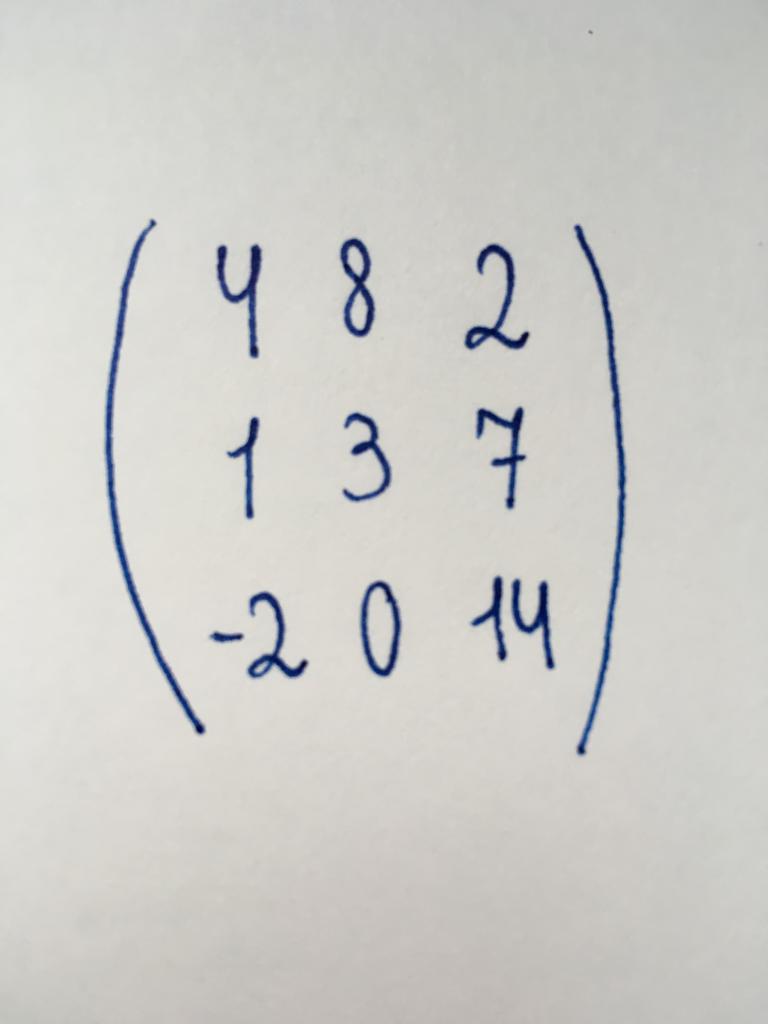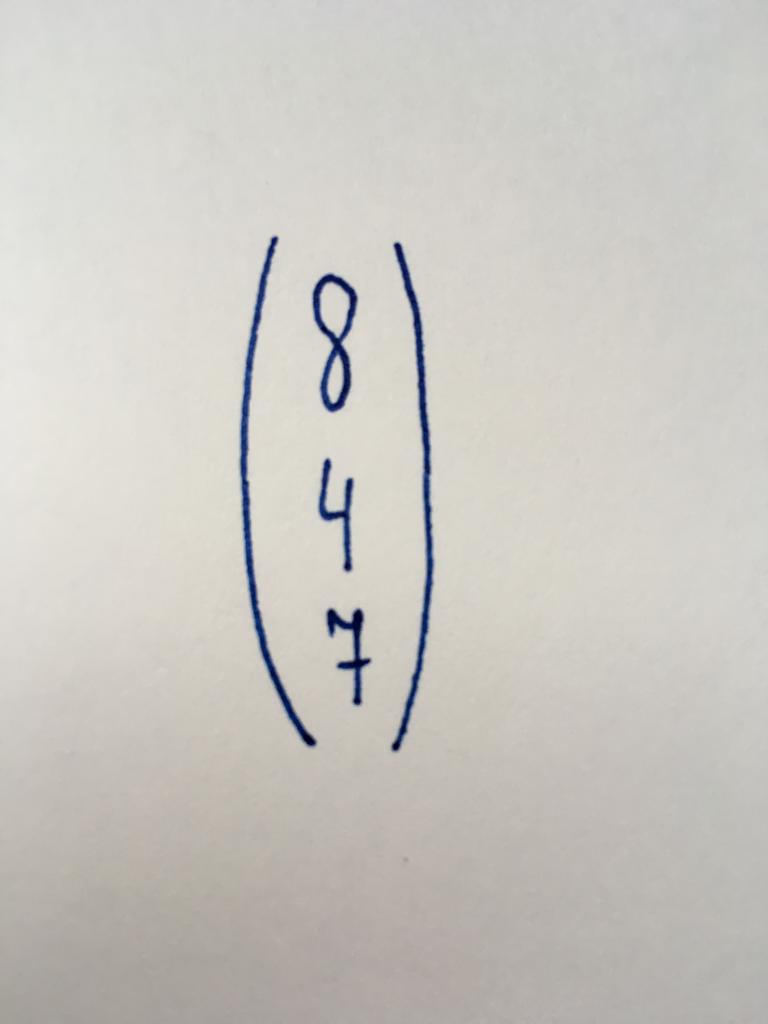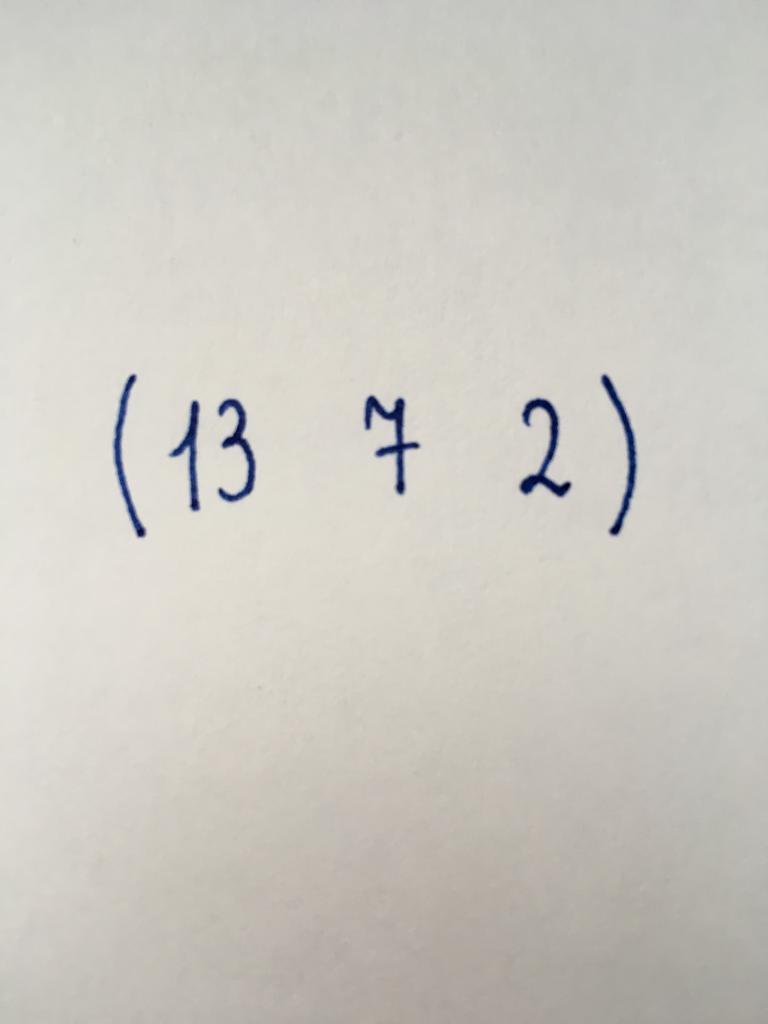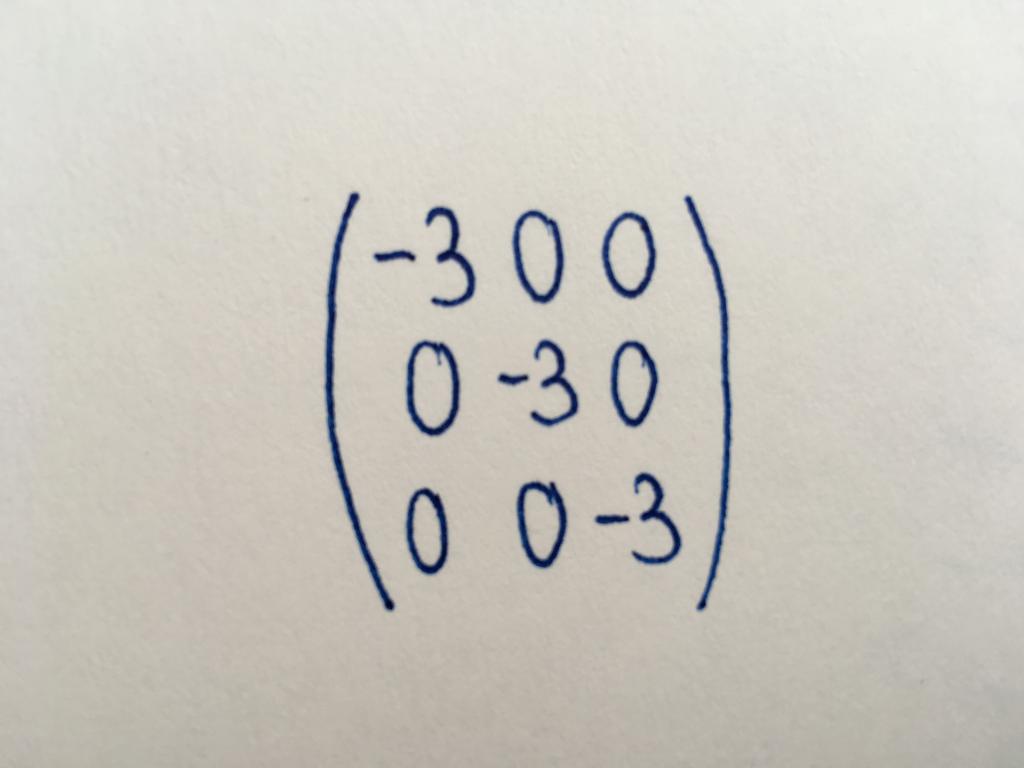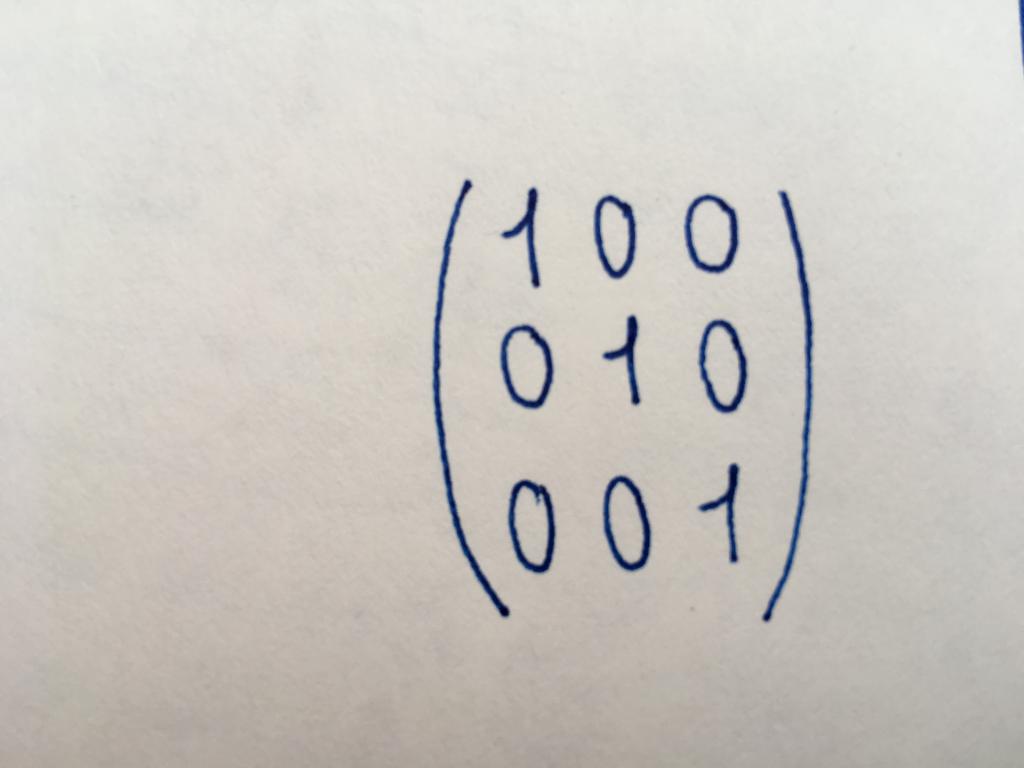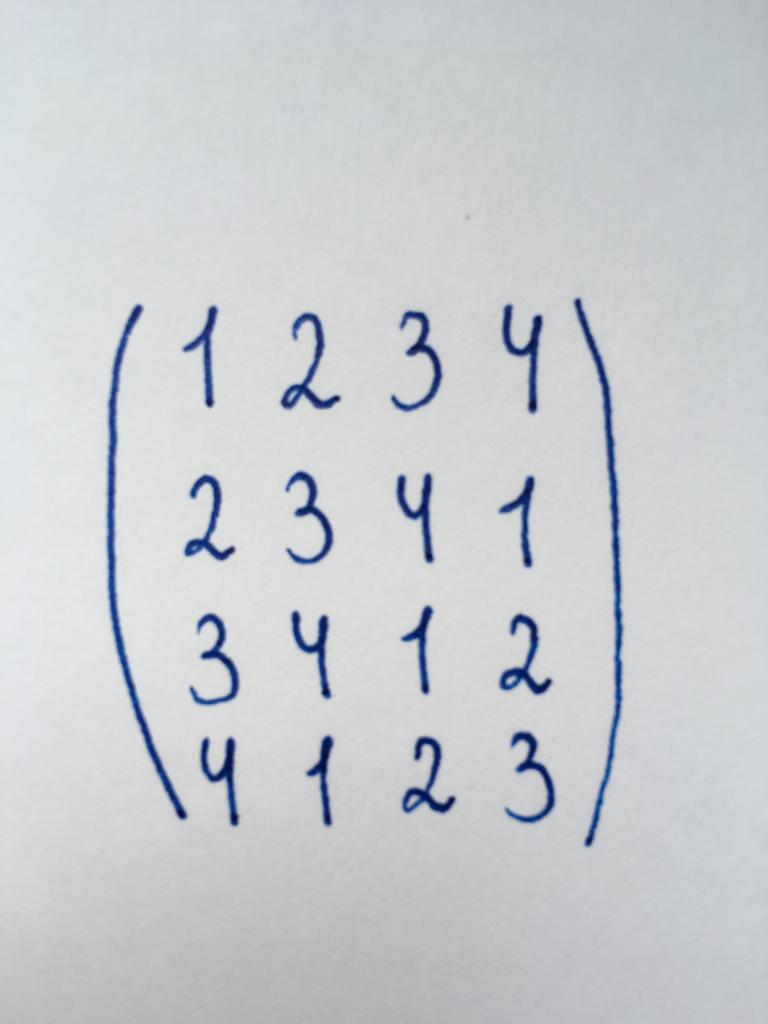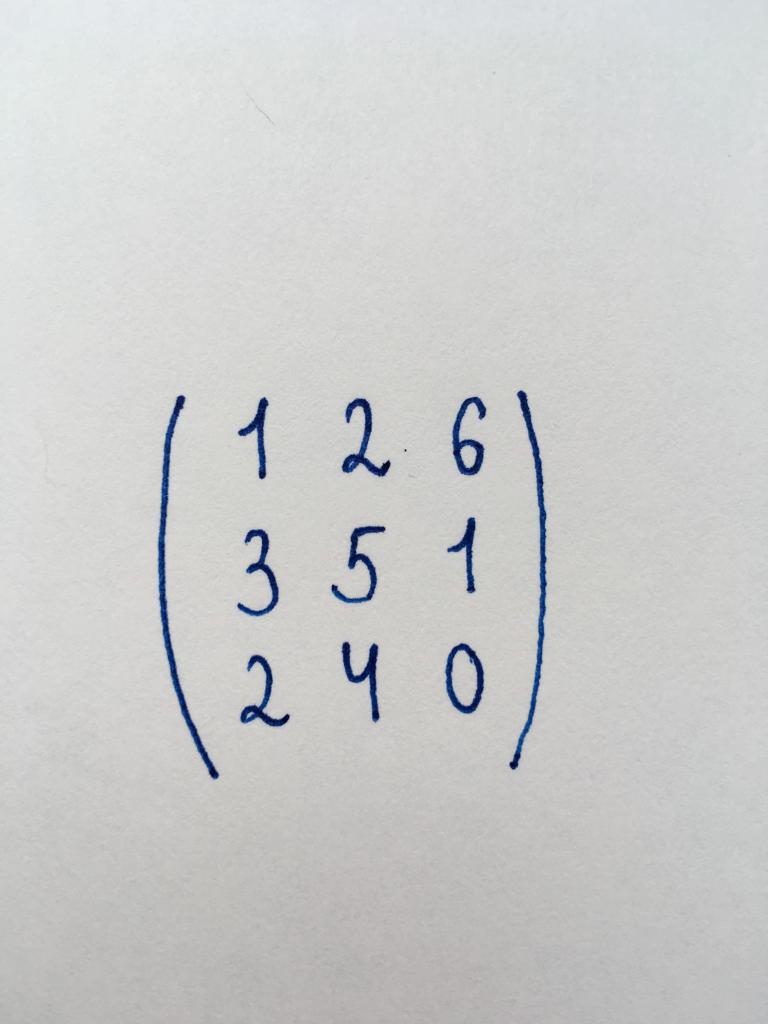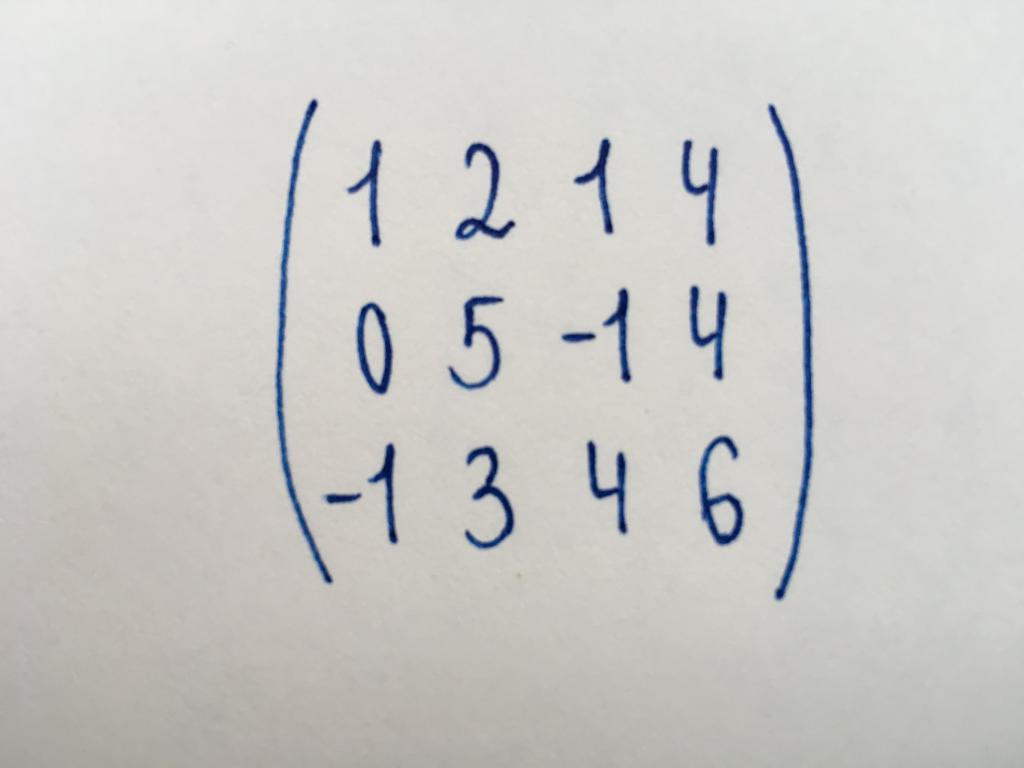Как найти определитель ступенчатой матрицы

Определители

Дадим индуктивное
определение определителя (разложением
по первой строке).

Определение.
Определителем (n-го
порядка) назовем отображение, которое
определено на множестве квадратных
матриц (размерности n×n),
принимает значения на множестве
действительных чисел и организовано
следующим образом:

при
квадратной матрице первого порядка
ставится в соответствие то число,
которое содержится в ее клетке, т. е.,
где– обозначение для определителя;
предполагая
определенными определители порядка
n,
где
,
определитель порядкаk
введем соотношением

Помимо
обозначения
также используются обозначенияи.

Теорема.
Определители
можно вычислять разложением по любому
столбцу или по любой строке, при этом
имеют место равенства:

где
()называется
минором ()-го
порядка,
соответствующим
элементу
()и является
определителем матрицы,
полученной
из матрицы А вычеркиванием
i—й
(k—й)
строки и
k—го
(j—го)
столбца.

Доказательство.
Если по определению определителя
расписать его миноры ()-го
порядка до сумм произведений чисел, то
можно увидеть, что результат не зависит
от того, разложением по какой строке
или какому столбцу мы пользовались при
сведениивычисления
определителя
n-го
порядка
к вычислению этих миноров.■

Теорема.
Если матрица
А
содержит
нулевую строку,
то определитель

.

Доказательство.
Если разложить определитель по нулевой
строке, то очевидно получим 0.■

Теорема.
Если от
матрицы А
к матрице
В
можно перейти
с помощью одного элементарного
преобразования строк первого типа,
то
.

Доказательство.
Пусть от матрицы А
к матрице В
можно перейти с помощью перемены местами
i-й
и j-й
строк. Разложив определители этих матриц
по i-й
строке, каждый из получившихся миноров
()-го
порядка разложим поj-й
строке. В результате увидим, что полученные
разложения будут отличаться только
знаками при слагаемых.■

Теорема.
Если матрица
А
содержит две
одинаковые строки, то определитель
.

Доказательство.
С одной
стороны, переставляя местами две
одинаковые строки, получим определитель,
отличающийся от исходного знаком. С
другой стороны, это тот же самый
определитель. Очевидно, только число 0
обладает таким свойством.■

Теорема.
Если от
матрицы А
к матрице
В
можно перейти
с помощью одного элементарного
преобразования строк второго типа,
то
.

Доказательство.

=()+…+

+()=

=+…++

=(+…+)=

=+==,

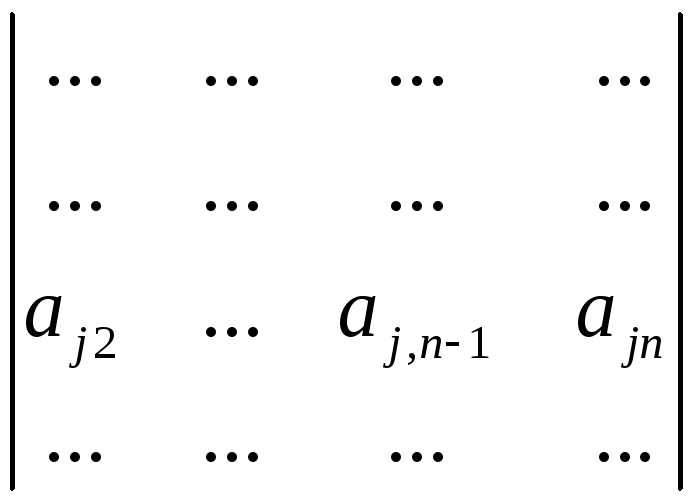
поскольку
один из определителей содержит две
одинаковых строки.■

Теорема.
Если от
матрицы А
к матрице
В
можно перейти
с помощью одного элементарного
преобразования строк третьего типа,
где
–соответствующий
коэффициент,
то
.

Доказательство.
Пусть от
матрицы А
к матрице В
можно перейти с помощью домножения i-й
строки на
.
Разложив определитель матрицы
В по i-й
строке и вынеся за скобки
,
в скобках получим разложение поi-й
строке определителя матрицы
А.■

Теорема.
Определитель
ступенчатой матрицы равен произведению
ее элементов, стоящих на главной
диагонали.

Доказательство.
Раскладывая определитель в соответствии
с его определением до сумм произведений
его элементов, учитывая определение
ступенчатого вида матрицы, убеждаемся,
что все слагаемые кроме одного наверняка
будут нулями. Оставшееся слагаемое есть
произведение элементов главной
диагонали.■

Теорема.
Определитель
матрицы А равен определителю
транспонированной матрицы
.

Доказательство.
Раскладывая определители матриц А
и

в соответствии с определением определителя
до сумм произведений элементов этих
матриц, получаем выражения, отличающиеся
только порядком слагаемых и порядком
множителей в слагаемых. Следовательно,
.■

Таким
образом, все теоремы о свойствах
определителя, доказанные для строк,
также имеют место и для столбцов.

Теорема.
Строки
(столбцы) квадратной матрицы линейно
независимы тогда и только тогда, когда
ее определитель отличен от нуля.

Доказательство.
Основываясь на свойствах определителя,
заметим, что если от квадратной матрицы
А
к квадратной матрице В
перешли с помощью элементарных
преобразований строк, то
определители
этих матриц либо оба нулевые, либо оба
ненулевые.

Если
строки матрицы А
размерности r
линейно независимы, то число ненулевых
строк в ее ступенчатом виде равно r.
Тогда число опорных элементов равно r.
Поскольку они стоят в разных строках и
столбцах, сдвигаясь с каждой строкой
направо, то опорные элементы совпадают
с элементами главной диагонали.
Следовательно, среди элементов главной
диагонали нет нулевых, а значит,
определитель ступенчатой матрицы
неравен нулю.

Обратно,
если определитель ступенчатой матрицы
неравен нулю, то среди элементов главной
диагонали нет нулевых. Тогда она не
имеет нулевых строк. Следовательно,
ранг матрицы А
равен ее размерности r,
т. е. строки матрицы А
линейно независимы.

Для
столбцов утверждение следует из того,
что
.■

Теорема.
У всякой
матрицы А ранга r
имеется r
линейно независимых столбцов,
и любой набор из более чем r
столбцов линейно зависим.

Доказательство.
Рассмотрим
минор М
порядка r,
составленный из элементов матрицы А,
находящихся на пересечении базисных
строк, и столбцов, в которых будут стоять
опорные элементы, если матрицу А
привести к ступенчатому виду с помощью
элементарных преобразований строк
(таких столбцов будет также r).
При приведении матрицы А
к ступенчатому виду Гаусса минор М
перейдет в минор
от единичной матрицы размерностиr.
Следовательно,
.
Тогда,
а значит, столбцы минораМ
линейно независимы. Получается, что
столбцы матрицы А,
содержащие столбцы минора М,
тоже линейно независимы.

Если
предположить, что имеется r+1
линейно независимый столбец матрицы
А,
то, взяв минор М
порядка r+1,
с элементами, принадлежащими этим
столбцам и какой-нибудь (r+1)-й
строке, получим, что минор М
имеет r+1
линейно независимый столбец, т. е.
.
При приведении матрицыА
к ступенчатому виду минор М
перейдет в минор
.
При этом.
Следовательно, ступенчатый вид матрицыА
имеет по крайней мере (r+1)-у
ненулевую строку, что противоречит
тому, что ранг матрицы А
равен r.■

Определение.
Говорят, что базисными
столбцами матрицы можно объявить
те ее столбцы, которые являются линейно
независимыми, а их число равно рангу
матрицы.

Определение.
Говорят, что
базисным
минором матрицы можно объявить
ее минор, элементы которого располагаются
на пересечении строк и столбцов, которые
можно объявить базисными.

Выбор
базисного минора, вообще говоря,
неоднозначен. Базисный минор неравен
нулю. Его порядок равен рангу матрицы.
Минор матрицы, порядок которого больше
порядка базисного минора, равен нулю.
Таким образом, ранг матрицы равен не
только максимальному числу линейно
независимых строк этой матрицы, но и
максимальному числу линейно независимых
столбцов этой матрицы, и максимальному
порядку отличного от нуля минора этой
матрицы. Также ранг матрицы А
равен рангу матрицы
,
транспонированной к матрицеА.

Источник

Теоретический минимум

Определитель (детерминант) возникает во многих разделах математики естественным образом. Вводится он обычно в рамках алгебры.
Например, можно начинать с систем линейных алгебраических уравнений (СЛАУ). Для простоты ограничимся случаем двух уравнений с
двумя переменными:
.
Решить эту систему легко, например, выражая одну из переменных через другую и выполняя подстановку во второе уравнение.

Решение удобно представить в другом виде, для чего вводится следующее обозначение:
.
Так вводится определитель второго порядка. В таких обозначениях получим из (1)
.
Это частный случай формул Крамера, предназначенных для решения СЛАУ, число уравнений в которых совпадает с числом переменных.
Мы не останавливаемся здесь подробно на вопросе решения СЛАУ. Заметим только, что понятие определителя обобщается для большего
количества элементов.

Обобщение такое может быть сделано не одним способом. Возможен индуктивный метод, когда определитель третьего порядка
вводится через определитель второго порядка, определитель четвёртого порядка — через определитель третьего порядка и т.д.
Например, для определителя третьего порядка вводится следующее правило:
.
Сформулировать правило можно следующим образом. Берётся первый элемент первой строки, вычёркивается строка и столбец, которым
этот элемент принадлежит — остаётся определитель второго порядка. Следующий элемент первой строки берётся со знаком минус, снова
вычёркивается строка и столбец, которым принадлежит элемент, остаётся определитель. Наконец, третий элемент первой строки берётся со
знаком плюс, опять вычёркиваются содержащие его строка и столбец. Соответственно, правило легко обобщить на определитель любого порядка.
Последовательно берутся элементы первой строки, причём знаки, с которыми они входят в определитель, должны чередоваться. Затем
вычёркивается строка и столбец, в которые входит выбранный элемент, остаётся определитель на единицу меньшего порядка.

С точки зрения вычислений этот метод введения определителя не так плох, но для доказательств свойств детерминанта это определение
неудобно, поэтому используется другое определение. Чтобы прийти к нему, выпишем явно определитель третьего порядка.

Обратите внимание: все слагаемые можно записать в общем виде . Индексы могут принимать
значения 1, 2 или 3. Фактически мы перебираем все возможных варианты расстановки трёх чисел. Таких вариантов шесть: 123, 132, 213, 231, 312, 321.
Слагаемых в определителе тоже шесть. Как определить знак, с которым войдёт в определитель слагаемое при данной расстановке индексов?
Возьмём за отправную точку слагаемое, в котором вторые индексы образуют последовательность 123 (элемент ).
Этот элемент входит со знаком плюс. Поменяем местами два вторых индекса, чтобы они образовали последовательность 213. Соответствующее
слагаемое входит в определитель со знаком минус. Если же мы в последовательности 123 дважды поменяем
местами индексы: , то получим слагаемое , входящее в определитель со знаком
плюс. Отсюда можно прийти к идее составления определителя на основе произведений его элементов, которые входят со знаком, определяемым
расстановкой индексов элементов в данном слагаемом. Сформулируем эту идею в общем виде для определителя порядка . Он будет состоять
из слагаемых вида , где индексы принимают значения от 1 до .
Вводится понятие перестановки индексов. Так называют упорядоченный набор чисел из чисел от 1 до без пропусков и повторений.
Два элемента перестановки образуют порядок, если при . В противном случае эти два элемента образуют инверсию.
Если в перестановке имеется чётное число инверсий, то она называется чётной, в противном случае — нечётной. Если мы меняем местами любые
два элемента перестановки, то это называется транспозицией. При транспозиции перестановка меняет свою чётность.

Теперь мы можем дать общее определение детерминанта. Введём в рассмотрение таблицу чисел (матрицу)
.
По определению её детерминантом называется число
,
где суммирование ведётся по всевозможным перестановкам , а — это число инверсий в перестановке .

Пример.
Определим, с каким знаком войдёт в определитель пятого порядка слагаемое .
Согласно общему определению нужно найти число инверсий в перестановке 34152. Удобнее всего делать это приведением перестановки к виду 12345,
считая при этом число транспозиций:
— 2 транспозиции
— 3 транспозиции
Итого 5 транспозиций, следовательно, перестановка была нечётная, и рассматриваемое слагаемое должно войти в определитель с минусом.

Переходим к свойствам определителя. Отметим, что здесь мы не останавливаемся на свойствах определителя, связанных с операциями над матрицами:
эти свойства обсудим позже.
1. При перестановке двух строк или столбцов определителя он меняет знак.
2. Определитель с двумя равными строками (столбцами) равен нулю.
3. Если к строке (столбцу) определителя прибавить другую строку (столбец) определителя, умноженную на отличное от нуля число,
то определитель не изменится.
4. Из строки (столбца) определителя можно выносить множитель за знак определителя.

Следующие свойства приведут нас к тому определению детерминанта, с которого мы начали. Сначала введём терминологию. Минором
элемента называется определитель, полученный вычёркиванием из исходного определителя строки и столбца, содержащих элемент .
Алгебраическое дополнение элемента
.
Существует теорема разложения определителя по строке и по столбцу. Согласно этой теореме определитель равен сумме элементов одной строки
(одного столбца), умноженных на их алгебраические дополнения. Например,
.
Видно, что это и есть то индуктивное определение детерминанта, которое приводилось выше. Однако теорема о разложении определителя позволяет
вычислять детерминант разложение не только по первой строке, а по любой строке или любому столбцу — как удобнее.
Другое следствие теоремы о разложении определителя — теорема об определителе верхнетреугольной матрицы, т.е. матрицы вида
.
Детерминант такой матрицы равен произведению её диагональных элементов. Отсюда следует способ вычисления определителей высоких порядков.
Нужно допустимыми преобразованиями привести матрицу к верхнетреугольному виду и перемножить диагональные элементы. К преобразованиям
относится прибавление к строкам и столбцам определителя других строк и столбцов, умноженных на соответствующие числа. Проиллюстрируем это примерами.

Примеры вычисления определителей

Пример 1. Вычисление определителей матриц прямым разложением по строкам и столбцам.
Вычислить определитель

Один раз покажем вычисление по теореме разложения, однако на практике обычно лучше не применять такой способ к вычислению
определителей выше третьего порядка (если только в определителе нет большого количества нулей).
Во втором столбце есть два нуля, поэтому разложение проводим по второму столбцу:

Первый определитель третьего порядка вычисляем разложением по первой строке (впрочем, этот вариант ничем не лучше разложений по другим
строкам или столбцам). Второй определитель раскладываем по второй строке: там есть один нуль (с тем же успехом можно было раскладывать по
второму столбцу):

Пример 2. Простой пример вычисления определителя методом преобразований.
Вычислить определитель
.

В общем, ничто не мешает применить совсем простую формулу для определителя второго порядка, но хотелось бы сделать вычисления проще.
Для этого вычтем из второго столбца первый, вынесем из второго столбца 100:
.

Пример 3. Вычисление определителей матриц методом преобразований.
Вычислим тот же определитель, что и в первом примере, но с помощью допустимых преобразований. Совершённые преобразования будут
указываться после их проведения.

Из второй и четвёртой строк вычли первую строку, из третьей строки вычли первую, умноженную на 2. Затем вынесли из второй строки двойку.
Умножили вторую строку на 5, четвёртую строку — на 2. Чтобы определитель не изменился, разделили его на 10. Этими действиями мы приводим
определитель к ступенчатому виду.

Внесли дробь перед определителем во вторую строку, третью строку умножили на 12, четвёртую — на 7; прибавили к четвёртой строке третью,
разделили третью строку на 12. Домножения и деления строк определителя сопровождались изменением множителя перед определителем.
Перемножение диагональных элементов и деление результата на 7 приводит к ответу 46 — в согласии с результатом вычислений в первом примере.
Может показаться, что мы ничего не выгадали по сравнению с первым примером, пользуясь методом преобразований. Иногда, действительно, вычисления
и тем, и другим способами примерно одинаковы по сложности. Разница становится очевидна при вычислении определителей бòльших порядков
или при отсутствии нулей среди элементов матрицы (см. далее).

Пример 4. Определитель матрицы без нулевых элементов.
Вычислить определитель

Применяем метод преобразований.

Умножили вторую, третью, четвёртую строки на 3 и вычли из них первую строку; вынесли из второй, третьей и четвёртой строк 2.

Умножили третью и четвёртую строки на 4, вычли из них вторую строку; вынесли из третьей и четвёртой строк 3.

Четвёртую строку умножили на 5 и вычли из неё третью строку.
Вычисление расписано очень детально, поэтому может показаться, что оно очень длинно. Между тем непосредственное разложение по строке
не будет короче и к тому же может быть связано с чисто арифметическими вычислительными ошибками.

Пример 5. Вычисление определителя пятого порядка.
Вычислить определитель
.

Хотелось бы сразу пояснить, что раскладывать этот определитель по строкам или столбцам — значит иметь дело с слагаемыми.
Поэтому будем преобразовывать определитель. Выкладки не будут столь детальны, как прежде. Рекомендуется проделать вычисления самостоятельно,
а ответ сравнить с полученным здесь:

Нужно подчеркнуть, что показанный метод, конечно же, не единственный возможный. Необязательно упорно приводить матрицу к ступенчатому
виду. Можно комбинировать метод преобразований с разложением по строкам и столбцам, получая нули там, где это удобнее для вычислений.
Здесь продемонстрирован метод последовательного приведения к ступенчатому виду матрицы.

Замечания.
1. В высшей алгебре приводится ещё один способ определения детерминанта, имеющий значительные преимущества по сравнению с приведёнными здесь. Он основан на использовании т.н. внешних произведений.
2. Теорема разложения имеет очень сильное обобщение — теорему Лапласа. Она заключается в возможности разложения определителя не только по строке, но и по минорам. Мы здесь не останавливаемся
на этой теореме.
Не возражая против слов процитированного В.И. Арнольда, замечу, что сейчас есть такое модное веяние — пытаться засунуть куда только
можно и нельзя теорию форм и всё тому подобное. Да, выделенное жирным шрифтом утверждение имеет место быть, с этим не поспоришь,
только вот вычислять детерминанты оно не поможет. А основной смысл приведённого выше текста сводился к мотивировке введения
детерминанта в том виде, в каком он вводится буквально с первых семинаров (делается это обычно без обоснования, а появляется оно
примерно полгода спустя). Также насколько возможно поясняется классическое определение, даваемое в алгебре, а акцент сделан на
вычислительной части — собственно на том, что нужнее всего студентам первого и второго семестров. Может быть со временем появится
набор тем, содержащих материал, который в МИФИ не дают.

С Арнольдом также не поспоришь в том, что геометрии сейчас уделяется слишком мало внимания, но это не значит, что некоторые чисто
алгебраические вещи должны извлекаться из процесса образования.
не хочется спорить, если честно, поэтому отвечу очень кратко

меня учили ( не в мифи), что определитель — это коэффициент преобразования объема под действием линейного оператора. Т.е., под действием линейного оператора А параллелепипед объемом X переходит в параллелепипед с (ориентированным) объемом det(A)*X

из этого определения мгновенно (без приложения каких-либо умственных усилий) следует что определитель произведения матриц равен произведению определителей, а для суммы матриц например это уже не верно. Из вашего определения это можно вывести, но это уже нетривально. И главное вывод выглядит как бессмысленная возня с индексами, он скорее прячет ясный смысл равенства, а не проясняет его. Также скажем следует, опять же без каких либо вычислений, что определитель матрицы, у которой два столбца или две строки совпадают, равен 0, многое следует про якобиан, про то что не бывает определителя у неквадратной матрицы ну итд

то, что я услышал правильное определение на почти 2 года позже мифишного, отняло у меня очень много ценного времени, поэтому я теперь так нервно реагирую когда вижу мифишное.

И вообще, это очень характерная ситуация, которую я неоднократно встречал в жизни. Если вы видите человека, который очень хорошо знает математику, то скорее всего это не потому, что он прорешал всего демидовича, а потому что он читал правильные книжки/учился у правильных людей в то время как другие решали демидовича.
rogue, я за принципиальные вещи с Вами не спорю. Я согласен с тем, что определение, которое приводится в линейной алгебре, во многих
теоретических вопросах неудобно, очень неудобно. Более того, я упомянул о существовании хорошего определения, имеющего выходы на разные
интересные общетеоретические вопросы в примечании. Но понимаете, цель вот этой конкретной темы как раз прояснить определение, которое студент
узнаёт на первом семестре и которое ему может быть непонятно. Цель этой конкретной темы — показать методы вычисления определителей.
Могу повторить, что была у меня мысль со временем — когда основные темы будут готовы — обратить внимание и на темы, которые в МИФИ не освещают,
к сожалению. Я согласен, что в МИФИ не хватает современной математики.

«Возня с индексами» — говорите Вы. Но с индексами-то тоже нужно уметь работать. А навык приобретается на практике, в качестве которой можно
рассматривать и доказательство таких вот теорем.

А это, простите, тривиальность.
я наверное не сумел донести свою мысль. Алгебраическое определение — вредное, оно сильно затрудняет понимание (и не каких-то теоретических вопросов, а самых что ни на есть практических) и ничего не дает, кроме бессмысленного вычислительного рецепта. Бессмысленного потому, что он применим только для матриц от 2х2 до 4х4, как вы правильно написали 5×5 уже слишком много.

Кстати, считать определители выше 3×3 руками, если мне не изменяет память, мне не приходилось в мифи по-моему (понятно что это были определители как функции какого-то параметра) И вообще считать рукми определители «численные» размером выше 3х3 — анахронизм сродни использованию логарифмической линейки. Кстати и эти определители 3х3 были якобианами при замене переменных в каких-то интегралах, так что и тут правильное определение было бы более полезным.

Одним словом изучать определители, основываясь на «классическом определении» (на самом деле оно никаким классическим не является конечно) — вредно для мозгов. Наверное чуть лучше чем какие-нибудь подстановки Эйлера, но не сильно. Но я понимаю, что признать это вы не сможете, поэтому как говорят джентельмены let’s agree to disagree

рад, что наши мнения тут совпадают
кстати, а как без использования геометрического определения объясняют почему векторное и смешанное произведения — определитель? вопрос абсолютно безо всякой подколки, я правда не знаю как это объяснить основываясь на алгебраическом определении
rogue, Вы себе противоречите. С одной стороны

а с другой стороны

Т.е. всё-таки для тех определителей, которые считать приходилось, определение пригодно, но потому оно и бессмысленно :huh:

Не существует «правильного» определения (если только речь не идёт о каких-то ошибках). Есть то, которое Вам больше нравится.
На мой взгляд ничего вредного в определении детерминанта, которое здесь обсуждается, нет. На первых порах нужен именно способ
вычисления определителей. Он прекрасно даётся самим определением, чем оно и хорошо. Другое дело, что оно только здесь и хорошо.
Но я ещё раз повторю: ничем Ваше «правильное определение» вычислению конкретных детерминантов не поможет. Поэтому для теории
оно хорошее и «правильное», для практики — абсолютно бессильное. Потому что все пользуются тем, что определитель произведения матриц
есть произведение определителей сомножителей. А как это доказать — для вычислений вопрос совершенно непринципиальный.

Не совсем понял вопрос. Вот есть вывод такой, что два вектора раскладываются по базису, векторно перемножаются с использованием
свойства линейности векторного произведения. Всё сводится к произведениям базисных векторов, которые легко вычисляются по
определению. Получается формула, в которой просматривается определитель. Это Вы геометрическим способом называете?
Den_Che
Корумчанин
Преподаватель МИФИ

А учебник кто-нибудь знает, где бы доказывалось в общем виде и для частных примеров (для матриц 2*2 и 3*3), что определитель — это площадь параллелепипеда? У меня получается очень громоздко уже для 2*2 и общего доказательства совершенно не просматривается
круто, т.е. объяснение такое что типа «просто так совпало, что просматривается определитель»? весело, да.
книжка, которую я читал в свое время это «Алгебра» Винберга. Еще есть очень хороший (англоязычный) учебник «Linear Algebra Done Wrong». но и там и там, насколько я помню подход обратный. сначала вводится геометрическое определение, потом из него выводится алгебраическая форма
Den_Che, насколько можно понять, скажем, из учебника Кострикина (специально посмотрел — освежил память),
для двумерного и трёхмерного случая это проверяется, как там сказано, прямым вычислением. А потом это свойство
распространяется на высшие размерности.

Для людей, не доверяющих из принципиальных соображений отечественным источникам, специально порылся в англоязычном
источнике, столь любимом аудиторией. Там написано следующее:

Там же, кстати, приводится простое доказательство для двумерного случая.Специально посмотрел сейчас в книге Постникова. Его такое доказательство устраивает. Лично для меня он больший авторитет, чем Вы.
rogue, Ваш подход к определению детерминанту безусловно верный. Только его придется обьяснять в завершении курса линейной алгебры, а перед этим работая только с линейными операторами.

Вообще непонятно зачем на мехмате (да и в мифи тоже) студентов учат дурацким навыкам вроде: быстрого вычисления определителся, собственных значений / векторов, вычислениям по тысячи пределов, интегралов и т.д.

Кстати по поводу детерминанта. Есть один момент. Как быть при n >= 4? Вы хотите сказать, что студенту будет удобнее умножать ортогональную составляющую односительно n-1 мерного подпространства на меру n-1 мерного параллелепипеда?

Schufter, В данном вами определении детерминанта мне не совсем понятно, зачем использовать инверсии, если можно определить подстановки, её разложение в произведении циклических, а далее легко определив четность подстановки. Не проще ли?
myjobisgop, вот смотрите: у Вас только одно перечисление того, сколько всего нужно ввести, заняло половину строки.
Я думаю, что проще не будет. Инверсии ничем не хуже и ничем не лучше в этом смысле. Я понимаю, что Вам хотелось бы видеть здесь подстановки,
чтобы был выход, скажем на группы и прочие вещи, если я правильно понял, конечно. Но ввести их никогда не поздно, а здесь это
необязательно и выигрыша не даст.

Я категорически несогласен с тем, что это «дурацкие навыки», но предлагаю в этой теме данный вопрос не обсуждать. Не о том она :huh:
Если хотите — откройте тему в учебном форуме.

Поделиться этой страницей

Источник

Матрица — это особый объект в математике. Изображается в форме прямоугольной или квадратной таблицы, сложенной из определенного числа строк и столбцов. В математике имеется большое разнообразие видов матриц, различающихся по размерам или содержанию. Числа ее строк и столбцов именуются порядками. Эти объекты употребляются в математике для упорядочивания записи систем линейных уравнений и удобного поиска их результатов. Уравнения с использованием матрицы решаются посредством метода Карла Гаусса, Габриэля Крамера, миноров и алгебраических дополнений, а также многими другими способами. Базовым умением при работе с матрицами является приведение к стандартному виду. Однако для начала давайте разберемся, какие виды матриц выделяют математики.

Нулевой тип

Все компоненты этого вида матрицы — нули. Между тем, число ее строк и столбцов абсолютно различно.

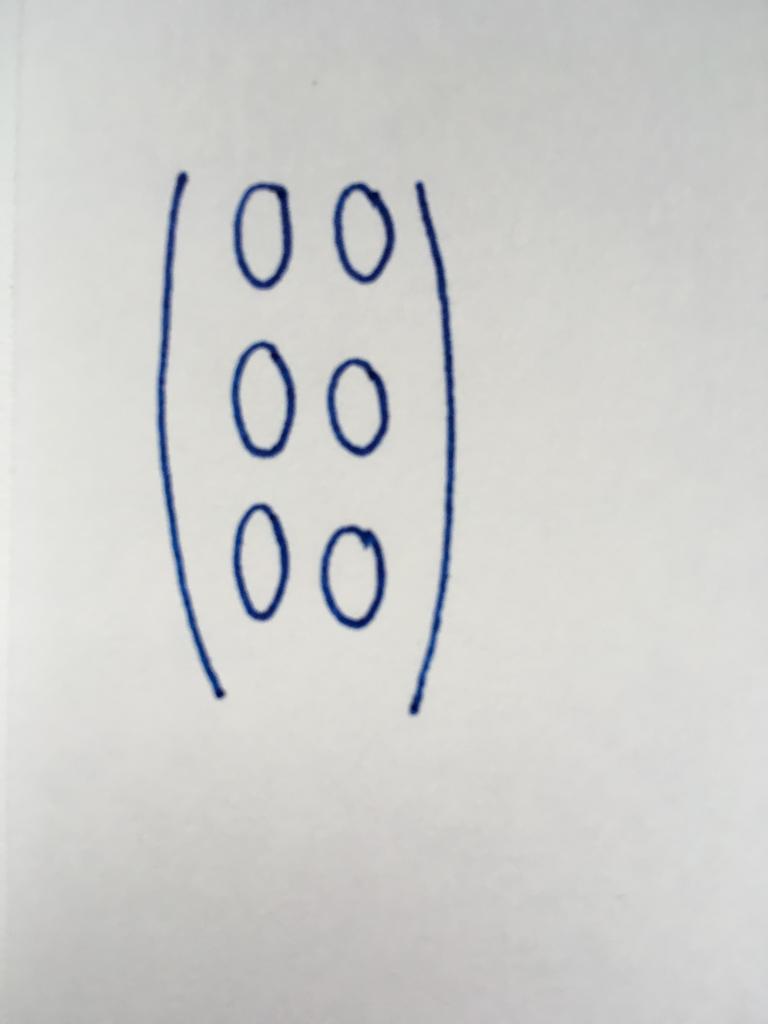
Квадратный тип

Количество столбцов и строк этого вида матрицы совпадает. Иначе говоря, она представляет собой таблицу формы «квадрат». Число ее столбцов (или строк) именуются порядком. Частными случаями считается существование матрицы второго порядка (матрица 2×2), четвертого порядка (4×4), десятого (10×10), семнадцатого (17×17) и так далее.

Вектор-стобец

Это один из простейших видов матриц, содержащий только один столбец, который включает в себя три численных значения. Она представляет ряд свободных членов (чисел, независимых от переменных) в системах линейных уравнений.

Вектор-строка

Вид, аналогичный предыдущему. Состоит из трех численных элементов, в свою очередь организованных в одну строку.

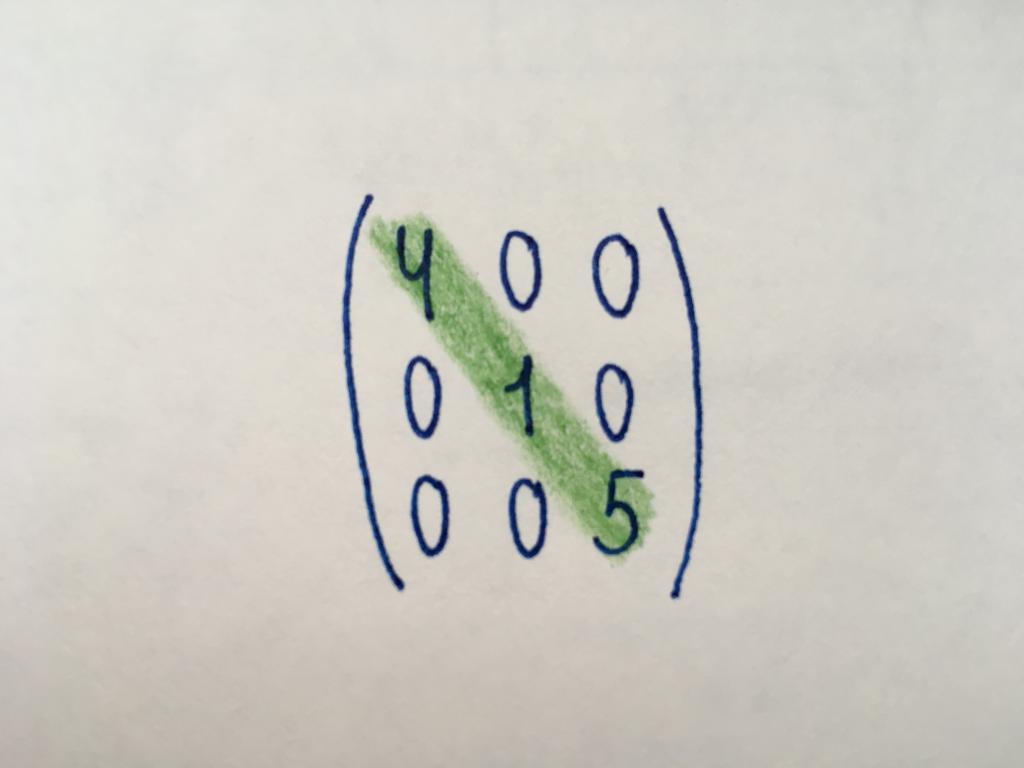
Диагональный тип

Числовые значения в диагональном виде матрицы принимают только компоненты главной диагонали (выделена зеленым цветом). Основная диагональ начинается с элемента, находящегося в левом верхнем углу, а заканчивается элементом в правом нижнем соответственно. Остальные компоненты равны нулю. Диагональный тип представляет собой только квадратную матрицу какого-либо порядка. Среди матриц диагонального вида можно выделить скалярную. Все ее компоненты принимают одинаковые значения.

Единичная матрица

Подвид диагональной матрицы. Все ее числовые значения являются единицами. Используя единичный тип матричных таблиц, выполняют ее базовые преобразования или находят матрицу, обратную исходной.

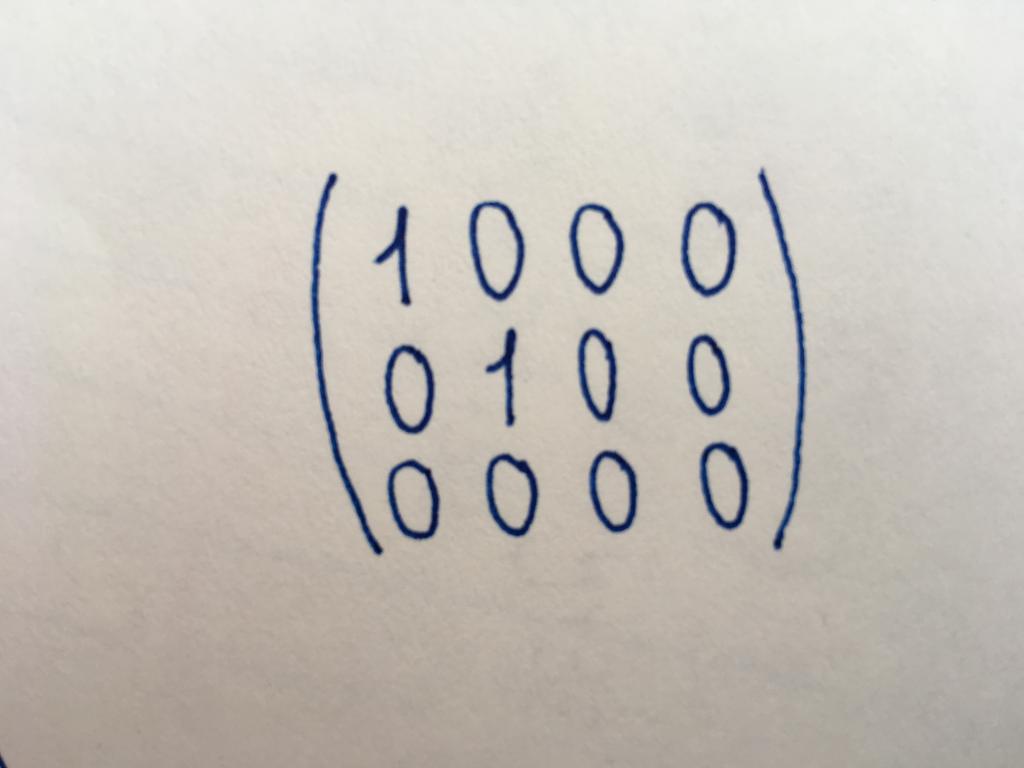
Канонический тип

Канонический вид матрицы считается одним из основных; приведение к нему часто необходимо для работы. Число строк и столбцов в канонической матрице различно, она необязательно принадлежит к квадратному типу. Она несколько похожа на единичную матрицу, однако в ее случае не все компоненты основной диагонали принимают значение, равное единице. Главнодиагональных единиц может быть две, четыре (все зависит от длины и ширины матрицы). Или единицы могут не иметься вовсе (тогда она считается нулевой). Остальные компоненты канонического типа, как и элементы диагонального и единичного, равны нулю.

Треугольный тип

Один из важнейших видов матрицы, применяемый при поиске ее детерминанта и при выполнении простейших операций. Треугольный тип происходит от диагонального, поэтому матрица также является квадратной. Треугольный вид матрицы подразделяют на верхнетреугольный и нижнетреугольный.

В верхнетреугольной матрице (рис. 1) только элементы, которые находятся над главной диагональю, принимают значение, равное нулю. Компоненты же самой диагонали и части матрицы, располагающейся под ней, содержат числовые значения.

В нижнетреугольной (рис. 2), наоборот, элементы, располагающиеся в нижней части матрицы, равны нулю.

Ступенчатая матрица

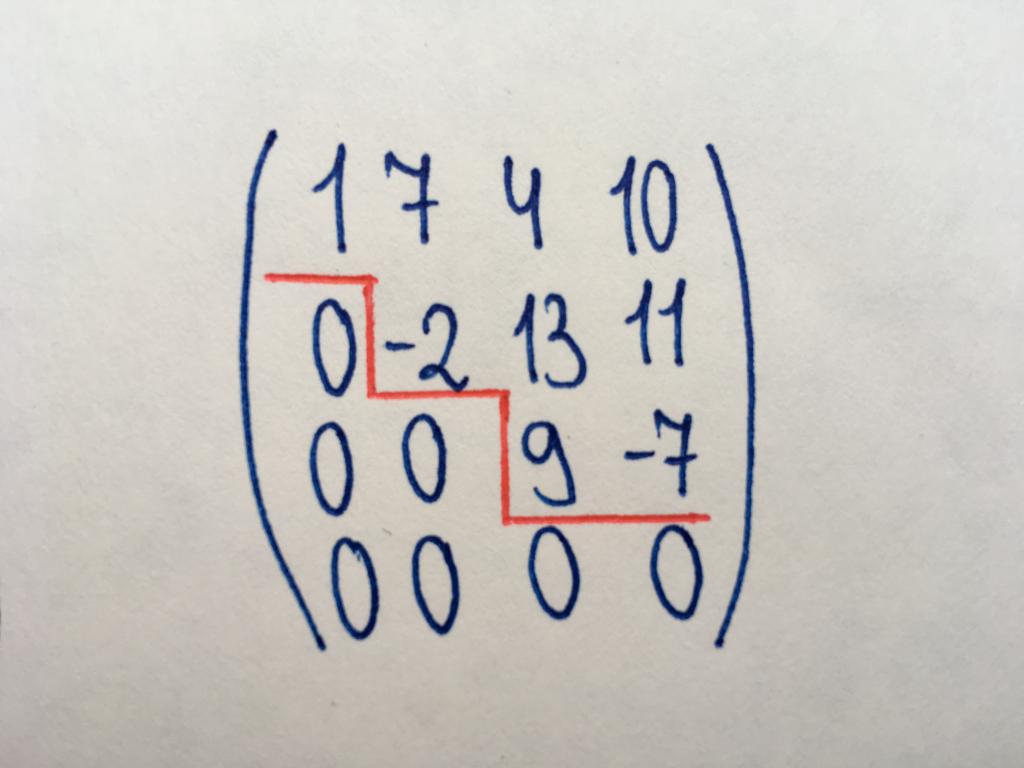
Вид необходим для нахождения ранга матрицы, а также для элементарных действий над ними (наряду с треугольным типом). Ступенчатая матрица названа так, потому что в ней содержатся характерные «ступени» из нулей (как показано на рисунке). В ступенчатом типе образуется диагональ из нулей (необязательно главная), и все элементы под данной диагональю тоже имеют значения, равные нулю. Обязательным условием является следующее: если в ступенчатой матрице присутствует нулевая строка, то остальные строки, находящиеся ниже нее, также не содержат числовых значений.

Таким образом, мы рассмотрели важнейшие типы матриц, необходимые для работы с ними. Теперь разберемся с задачей преобразования матрицы в требуемую форму.

Приведение к треугольному виду

Как же привести матрицу к треугольному виду? Чаще всего в заданиях нужно преобразовать матрицу в треугольный вид, чтобы найти ее детерминант, по-другому называемый определителем. Выполняя данную процедуру, крайне важно «сохранить» главную диагональ матрицы, потому что детерминант треугольной матрицы равен именно произведению компонентов ее главной диагонали. Напомню также альтернативные методы нахождения определителя. Детерминант квадратного типа находится при помощи специальных формул. Например, можно воспользоваться методом треугольника. Для других матриц используют метод разложения по строке, столбцу или их элементам. Также можно применять метод миноров и алгебраических дополнений матрицы.

Подробно разберем процесс приведения матрицы к треугольному виду на примерах некоторых заданий.

Задание 1

Необходимо найти детерминант представленной матрицы, используя метод приведения его к треугольному виду.

Данная нам матрица представляет собой квадратную матрицу третьего порядка. Следовательно, для ее преобразования в треугольную форму нам понадобится обратить в нуль два компонента первого столбца и один компонент второго.

Чтобы привести ее к треугольному виду, начнем преобразование с левого нижнего угла матрицы — с числа 6. Чтобы обратить его в нуль, умножим первую строку на три и вычтем ее из последней строки.

Важно! Верхняя строка не изменяется, а остается такой же, как и в исходной матрице. Записывать строку, в четыре раза большую исходной, не нужно. Но значения строк, компоненты которых нужно обратить в нуль, постоянно меняются.

Далее займемся следующим значением — элементом второй строки первого столбца, числом 8. Умножим первую строку на четыре и вычтем ее из второй строки. Получим нуль.

Осталось только последнее значение — элемент третьей строки второго столбца. Это число (-1). Чтобы обратить его в нуль, из первой строки вычтем вторую.

Выполним проверку:

detA = 2 x (-1) x 11 = -22.

Значит, ответ к заданию: -22.

Задание 2

Нужно найти детерминант матрицы методом приведения его к треугольному виду.

Представленная матрица принадлежит к квадратному типу и является матрицей четвертого порядка. Значит, необходимо обратить в нуль три компонента первого столбца, два компонента второго столбца и один компонент третьего.

Начнем приведение ее с элемента, находящегося в нижнем углу слева, — с числа 4. Нам нужно обратить данное число в нуль. Удобнее всего сделать это, умножив на четыре верхнюю строку, а затем вычесть ее из четвертой. Запишем итог первого этапа преобразования.

Итак, компонент четвертой строки обращен в нуль. Перейдем к первому элементу третьей строки, к числу 3. Выполняем аналогичную операцию. Умножаем на три первую строку, вычитаем ее из третьей строки и записываем результат.

Далее видим число 2 во второй строке. Повторяем операцию: умножаем верхнюю строку на два и вычитаем ее из второй.

Нам удалось обратить в нуль все компоненты первого столбца данной квадратной матрицы, за исключением числа 1 — элемента главной диагонали, не требующего преобразования. Теперь важно сохранить полученные нули, поэтому будем выполнять преобразования со строками, а не со столбцами. Перейдем ко второму столбцу представленной матрицы.

Снова начнем с нижней части — с элемента второго столбца последней строки. Это число (-7). Однако в данном случае удобнее начать с числа (-1) — элемента второго столбца третьей строки. Чтобы обратить его в нуль, вычтем из третьей строки вторую. Затем умножим вторую строку на семь и вычтем ее из четвертой. Мы получили нуль вместо элемента, расположенного в четвертой строке второго столбца. Теперь перейдем к третьему столбцу.

В данном столбце нам нужно обратить в нуль только одно число — 4. Сделать это несложно: просто прибавляем к последней строке третью и видим необходимый нам нуль.

После всех произведенных преобразований мы привели предложенную матрицу к треугольному виду. Теперь, чтобы найти ее детерминант, нужно только произвести умножение получившихся элементов главной диагонали. Получаем: detA = 1 x (-1) x (-4) x 40 = 160. Следовательно, решением является число 160.

Итак, теперь вопрос приведения матрицы к треугольному виду вас не затруднит.

Приведение к ступенчатому виду

При элементарных операциях над матрицами ступенчатый вид является менее «востребованным», чем треугольный. Чаще всего он используется для нахождения ранга матрицы (т. е. количества ее ненулевых строк) или для определения линейно зависимых и независимых строк. Однако ступенчатый вид матрицы является более универсальным, так как подходит не только для квадратного типа, но и для всех остальных.

Чтобы привести матрицу к ступенчатому виду, сначала нужно найти ее детерминант. Для этого подойдут вышеназванные методы. Цель нахождения детерминанта такова: выяснить, можно ли преобразовать ее в ступенчатый вид матрицы. Если детерминант больше или меньше нуля, то можно спокойно приступать к заданию. Если же он равен нулю, выполнить приведение матрицы к ступенчатому виду не получится. В таком случае нужно проверить, нет ли ошибок в записи или в преобразованиях матрицы. Если подобных неточностей нет, задание решить невозможно.

Рассмотрим, как привести матрицу к ступенчатому виду на примерах нескольких заданий.

Задание 1. Найти ранг данной матричной таблицы.

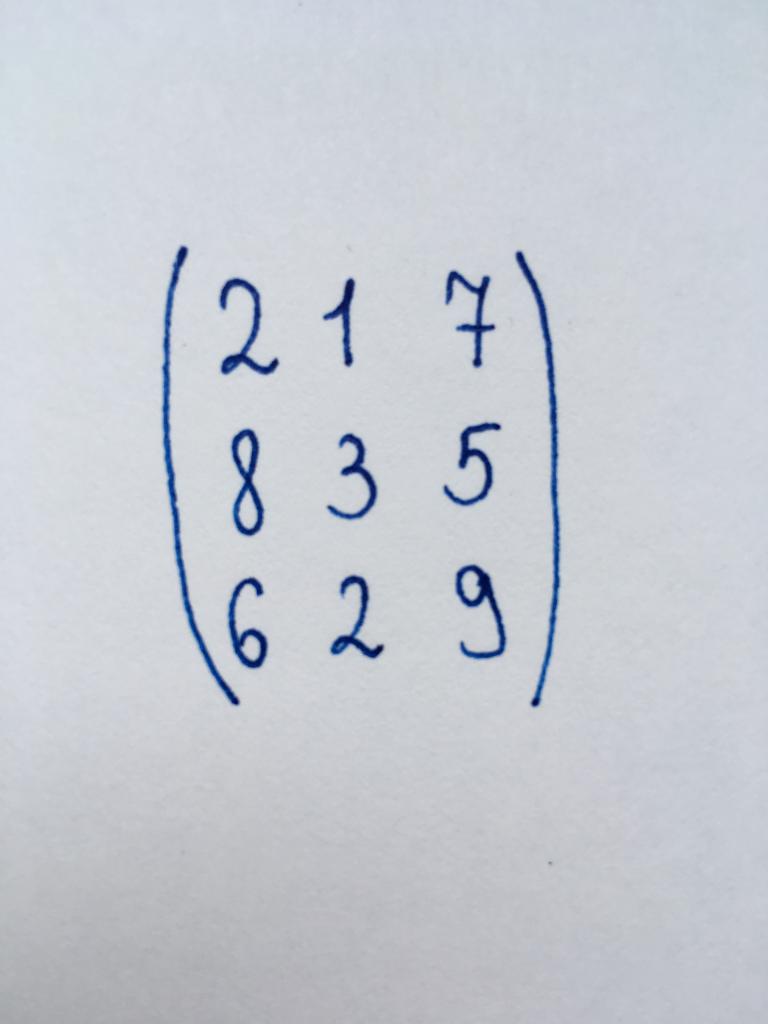
Перед нами квадратная матрица третьего порядка (3×3). Мы знаем, что для нахождения ранга необходимо привести ее к ступенчатому виду. Поэтому сначала нам необходимо найти детерминант матрицы. Воспользуемся методом треугольника: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) — (1 x 1 x 4) — (2 x 3 x 0) — (6 x 5 x 2) = 12.

Детерминант = 12. Он больше нуля, значит, матрицу можно привести к ступенчатому виду. Приступим к ее преобразованиям.

Начнем его с элемента левого столбца третьей строки — числа 2. Умножаем верхнюю строку на два и вычитаем ее из третьей. Благодаря этой операции как нужный нам элемент, так и число 4 — элемент второго столбца третьей строки — обратились в нуль.

Далее обращаем в нуль элемент второй строки первого столбца — число 3. Для этого умножаем верхнюю строку на три и вычитаем ее из второй.

Мы видим, что в результате приведения образовалась треугольная матрица. В нашем случае продолжить преобразование нельзя, так как остальные компоненты не удастся обратить в нуль.

Значит, делаем вывод, что количество строк, содержащих числовые значения, в данной матрице (или ее ранг) — 3. Ответ к заданию: 3.

Задание 2. Определить количество линейно независимых строк данной матрицы.

Нам требуется найти такие строки, которые нельзя какими-либо преобразованиями обратить в нуль. Фактически нам нужно найти количество ненулевых строк, или ранг представленной матрицы. Для этого выполним ее упрощение.

Мы видим матрицу, не принадлежащую к квадратному типу. Она имеет размеры 3×4. Начнем приведение также с элемента левого нижнего угла — числа (-1).

Прибавляем первую строку к третьей. Далее вычитаем из нее вторую, чтобы обратить число 5 в нуль.

Дальнейшие ее преобразования невозможны. Значит, делаем вывод, что количество линейно независимых строк в ней и ответ к заданию — 3.

Теперь приведение матрицы к ступенчатому виду не является для вас невыполнимым заданием.

На примерах данных заданий мы разобрали приведение матрицы к треугольному виду и ступенчатому виду. Чтобы обратить в нуль нужные значения матричных таблиц, в отдельных случаях требуется проявить фантазию и правильно преобразовать их столбцы или строки. Успехов вам в математике и в работе с матрицами!

Источник

Если вы приступили к изучению данной темы, то вы уже знакомы с понятием определителя матрицы и умеете находить определители первого, второго и третьего порядка.

Прежде чем начать рассмотрение новой темы, рекомендуется повторить правило вычисления определителя по строке и столбцу, рассматривающееся в теме «Как вычислить определитель матрицы третьего порядка», свойства определителей, а также нахождение миноров и алгебраических дополнений.

Разложение определителей по строкам или столбцам

Для вычисления определителей высших порядков применяется способ разложения определителя по строке или столбцу. Это позволяет представить детерминант в виде суммы произведений элементов какой-либо его строки или столбца на соответствующие этим элементам алгебраические дополнения. В таком случае вычисление определителя nn-го порядка сводится к вычислению определителей n−1n-1-го порядка.

Пример 1

Найти определитель ∣32454−32−45−2−3−7−3429∣begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix} двумя способами:

по 2-й строке;
по 3-у столбцу.

1 способ. Разложим определитель 4-го порядка по строке №2 и вычислим его:

∣32454−32−45−2−3−7−3429∣=4(−1)2+1∣245−2−3−7429∣+(−3)(−1)2+2∣3455−3−7−329∣+2(−1)2+3∣3255−2−7−349∣+(−4)(−1)2+4∣3245−2−3−342∣=begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix}=4(-1)^{2+1}begin{vmatrix}2&4&5\-2&-3&-7\4&2&9end{vmatrix}+(-3)(-1)^{2+2}begin{vmatrix}3&4&5\5&-3&-7\-3&2&9end{vmatrix}+2(-1)^{2+3}begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}+(-4)(-1)^{2+4}begin{vmatrix}3&2&4\5&-2&-3\-3&4&2end{vmatrix}=

=−4∣245−2−3−7429∣−3∣3455−3−7−329∣−2∣3255−2−7−349∣−4∣3245−2−3−342∣=−4(−54−20−112+60+28+72)−3(−81+50+84−45+42−180)−2(−54+100+42−30+84−90)−4(−12+80+18−24+36−20)=−4(−26)−3(−130)−2⋅52−4⋅78=104+390−104−312=78=-4begin{vmatrix}2&4&5\-2&-3&-7\4&2&9end{vmatrix}-3begin{vmatrix}3&4&5\5&-3&-7\-3&2&9end{vmatrix}-2begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}-4begin{vmatrix}3&2&4\5&-2&-3\-3&4&2end{vmatrix}=-4(-54-20-112+60+28+72)-3(-81+50+84-45+42-180)-2(-54+100+42-30+84-90)-4(-12+80+18-24+36-20)=-4(-26)-3(-130)-2cdot52-4cdot78=104+390-104-312=78.

2 способ. Разложим определитель 4-го порядка по 3 столбцу и вычислим его:

∣32454−32−45−2−3−7−3429∣=4(−1)1+3∣4−3−45−2−7−349∣+2(−1)2+3∣3255−2−7−349∣+(−3)(−1)3+3∣3254−3−4−349∣+2(−1)4+3∣3254−3−45−2−7∣=begin{vmatrix}3&2&4&5\4&-3&2&-4\5&-2&-3&-7\-3&4&2&9end{vmatrix}=4(-1)^{1+3}begin{vmatrix}4&-3&-4\5&-2&-7\-3&4&9end{vmatrix}+2(-1)^{2+3}begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}+(-3)(-1)^{3+3}begin{vmatrix}3&2&5\4&-3&-4\-3&4&9end{vmatrix}+2(-1)^{4+3}begin{vmatrix}3&2&5\4&-3&-4\5&-2&-7end{vmatrix}=

=4∣4−3−45−2−7−349∣−2∣3255−2−7−349∣−3∣3254−3−4−349∣−2∣3254−3−45−2−7∣=4(−72−80−63+24+112+135)−2(−54+100+42−30+84−90)−3(−81+80+24−45+48−72)−2(63−40−40+75−24+56)=4⋅56−2⋅52−3⋅(−45)−2⋅90=224−104+138−180=78=4begin{vmatrix}4&-3&-4\5&-2&-7\-3&4&9end{vmatrix}-2begin{vmatrix}3&2&5\5&-2&-7\-3&4&9end{vmatrix}-3begin{vmatrix}3&2&5\4&-3&-4\-3&4&9end{vmatrix}-2begin{vmatrix}3&2&5\4&-3&-4\5&-2&-7end{vmatrix}=4(-72-80-63+24+112+135)-2(-54+100+42-30+84-90)-3(-81+80+24-45+48-72)-2(63-40-40+75-24+56)=4cdot56-2cdot52-3cdot(-45)-2cdot90=224-104+138-180=78.

Метод понижения порядка

Для упрощения расчетов при вычислении определителей рекомендуется применять их свойства. Рассмотрим примеры вычисления определителей с применением их свойств.

Пример 1

Вычислить определитель

∣638−45642034241−46∣begin{vmatrix}6&3&8&-4\5&6&4&2\0&3&4&2\4&1&-4&6end{vmatrix}.

Вынесем из столбца №3 множитель 4:

∣638−45642034241−46∣=4⋅∣632−45612031241−16∣begin{vmatrix}6&3&8&-4\5&6&4&2\0&3&4&2\4&1&-4&6end{vmatrix}=4cdotbegin{vmatrix}6&3&2&-4\5&6&1&2\0&3&1&2\4&1&-1&6end{vmatrix}.

Вынесем из столбца №4 множитель 2:

4⋅∣632−45612031241−16∣=4⋅2⋅∣632−25611031141−13∣=8⋅∣632−25611031141−13∣4cdotbegin{vmatrix}6&3&2&-4\5&6&1&2\0&3&1&2\4&1&-1&6end{vmatrix}=4cdot2cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}.

Прибавим к строке №1 строку №2, умноженную на -2:

8⋅∣632−25611031141−13∣=8⋅∣−4−90−45611031141−13∣8cdotbegin{vmatrix}6&3&2&-2\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}.

Прибавим к строке №3 строку №2, умноженную на -1:

8⋅∣−4−90−45611031141−13∣=8⋅∣−4−90−45611−5−30041−13∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\0&3&1&1\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\4&1&-1&3end{vmatrix}.

Прибавим к строке №4 строку №2, умноженную на 1:

8⋅∣−4−90−45611−5−30041−13∣=8⋅∣−4−90−45611−5−3009704∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\4&1&-1&3end{vmatrix}=8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\9&7&0&4end{vmatrix}.

Разложим определитель по столбцу №3:

8⋅∣−4−90−45611−5−3009704∣=8⋅1⋅(−1)2+3∣−4−9−4−5−30974∣=8⋅(−1)5∣−4−9−4−5−30974∣=−8∣−4−9−4−5−30974∣8cdotbegin{vmatrix}-4&-9&0&-4\5&6&1&1\-5&-3&0&0\9&7&0&4end{vmatrix}=8cdot1cdot(-1)^{2+3}begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=8cdot(-1)^{5}begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=-8begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}.

Прибавим к строке №1 строку №3, умноженную на 1:

−8∣−4−9−4−5−30974∣=−8∣5−20−5−30974∣-8begin{vmatrix}-4&-9&-4\-5&-3&0\9&7&4end{vmatrix}=-8begin{vmatrix}5&-2&0\-5&-3&0\9&7&4end{vmatrix}.

Разложим определитель по столбцу №3 и вычислим его:

−8∣5−20−5−30974∣=−8⋅4⋅(−1)3+3∣5−2−5−3∣=−32⋅(−1)6∣5−2−5−3∣=−32∣5−2−5−3∣-8begin{vmatrix}5&-2&0\-5&-3&0\9&7&4end{vmatrix}=-8cdot4cdot(-1)^{3+3}begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32cdot(-1)^{6}begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32begin{vmatrix}5&-2\-5&-3end{vmatrix}.

Прибавим к строке №2 строку №1, умноженную на 1:

−32∣5−2−5−3∣=−32∣5−20−5∣-32begin{vmatrix}5&-2\-5&-3end{vmatrix}=-32begin{vmatrix}5&-2\0&-5end{vmatrix}.

Разложим определитель по столбцу №1 и заменим определитель 1-го порядка единственным его элементом:

−32∣5−20−5∣=−32⋅5⋅(−1)1+1⋅(−5)=−32⋅5⋅1⋅(−5)=800-32begin{vmatrix}5&-2\0&-5end{vmatrix}=-32cdot5cdot(-1)^{1+1}cdot(-5)=-32cdot5cdot1cdot(-5)=800.

Пример 2

Вычислить определитель

∣44−10−18237523325732122112176657211221∣begin{vmatrix}4&4&-1&0&-1&8\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №1 строку №4, умноженную на -4:

∣44−10−18237523325732122112176657211221∣=∣0−4−9−4−50237523325732122112176657211221∣begin{vmatrix}4&4&-1&0&-1&8\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №2 строку №4, умноженную на -2:

∣0−4−9−4−50237523325732122112176657211221∣=∣0−4−9−4−500−1330−1325732122112176657211221∣begin{vmatrix}0&-4&-9&-4&-5&0\2&3&7&5&2&3\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №3 строку №4, умноженную на -3:

∣0−4−9−4−500−1330−1325732122112176657211221∣=∣0−4−9−4−500−1330−10−4−140−4122112176657211221∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\3&2&5&7&3&2\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №5 строку №4, умноженную на -1:

∣0−4−9−4−500−1330−10−4−140−4122112176657211221∣=∣0−4−9−4−500−1330−10−4−140−4122112054545211221∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\1&7&6&6&5&7\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\2&1&1&2&2&1end{vmatrix}.

Прибавим к строке №6 строку №4, умноженную на -2:

∣0−4−9−4−500−1330−10−4−140−4122112054545211221∣=∣0−4−9−4−500−1330−10−4−140−41221120545450−3−300−3∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\2&1&1&2&2&1end{vmatrix}=begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\0&-3&-3&0&0&-3end{vmatrix}.

Разложим определитель по 1 столбцу:

∣0−4−9−4−500−1330−10−4−140−41221120545450−3−300−3∣=1⋅(−1)4+1∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣=−∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣begin{vmatrix}0&-4&-9&-4&-5&0\0&-1&3&3&0&-1\0&-4&-1&4&0&-4\1&2&2&1&1&2\0&5&4&5&4&5\0&-3&-3&0&0&-3end{vmatrix}=1cdot(-1)^{4+1}begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.

Прибавим к строке №1 строку №3, умноженную на -1:

−∣−4−9−4−50−1330−1−4−140−454545−3−300−3∣=−∣0−8−8−54−1330−1−4−140−454545−3−300−3∣-begin{vmatrix}-4&-9&-4&-5&0\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.

Прибавим к строке №3 строку №2, умноженную на -4:

−∣0−8−8−54−1330−1−4−140−454545−3−300−3∣=−∣0−8−8−54−1330−10−13−80054545−3−300−3∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\-4&-1&4&0&-4\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}.

Прибавим к строке №4 строку №2, умноженную на 5:

−∣0−8−8−54−1330−10−13−80054545−3−300−3∣=−∣0−8−8−54−1330−10−13−8000192040−3−300−3∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\5&4&5&4&5\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\-3&-3&0&0&-3end{vmatrix}.

Прибавим у строке №5 строку №2, умноженную на -3:

−∣0−8−8−54−1330−10−13−8000192040−3−300−3∣=−∣0−8−8−54−1330−10−13−80001920400−12−900∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\-3&-3&0&0&-3end{vmatrix}=-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\0&-12&-9&0&0end{vmatrix}.

Разложим определитель по 1 столбцу:

−∣0−8−8−54−1330−10−13−80001920400−12−900∣=−(−1)⋅(−1)2+1∣−8−8−54−13−800192040−12−900∣=(−1)3∣−8−8−54−13−800192040−12−900∣=−∣−8−8−54−13−800192040−12−900∣-begin{vmatrix}0&-8&-8&-5&4\-1&3&3&0&-1\0&-13&-8&0&0\0&19&20&4&0\0&-12&-9&0&0end{vmatrix}=-(-1)cdot(-1)^{2+1}begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=(-1)^{3}begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=-begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}.

Вынесем множитель -3 из строки №4:

−∣−8−8−54−13−800192040−12−900∣=−(−3)∣−8−8−54−13−8001920404300∣=3∣−8−8−54−13−8001920404300∣-begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\-12&-9&0&0end{vmatrix}=-(-3)begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}=3begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}.

Разложим определитель по 4 столбцу:

3∣−8−8−54−13−8001920404300∣=3⋅4⋅(−1)1+4∣−13−8019204430∣=12⋅(−1)5∣−13−8019204430∣=−12∣−13−8019204430∣3begin{vmatrix}-8&-8&-5&4\-13&-8&0&0\19&20&4&0\4&3&0&0end{vmatrix}=3cdot4cdot(-1)^{1+4}begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=12cdot(-1)^{5}begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=-12begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}.

Разложим определитель по столбцу №3 и вычислим его:

−12∣−13−8019204430∣=−12⋅4⋅(−1)2+3∣−13−843∣=−48⋅(−1)5∣−13−843∣=48∣−13−843∣-12begin{vmatrix}-13&-8&0\19&20&4\4&3&0end{vmatrix}=-12cdot4cdot(-1)^{2+3}begin{vmatrix}-13&-8\4&3end{vmatrix}=-48cdot(-1)^{5}begin{vmatrix}-13&-8\4&3end{vmatrix}=48begin{vmatrix}-13&-8\4&3end{vmatrix}.

Прибавим к строке №1 строку №2, умноженную на 3:

48∣−13−843∣=48∣−1143∣48begin{vmatrix}-13&-8\4&3end{vmatrix}=48begin{vmatrix}-1&1\4&3end{vmatrix}.

Прибавим к строке №2 строку №1, умноженную на 4:

48∣−1143∣=48∣−1107∣48begin{vmatrix}-1&1\4&3end{vmatrix}=48begin{vmatrix}-1&1\0&7end{vmatrix}.

Разложим определитель по столбцу №1 и заменим определитель 1-го порядка единственным его элементом:

48∣−1107∣=48⋅(−1)⋅(−1)1+1⋅7=48⋅(−1)⋅1⋅7=−33648begin{vmatrix}-1&1\0&7end{vmatrix}=48cdot(-1)cdot(-1)^{1+1}cdot7=48cdot(-1)cdot1cdot7=-336
.

Приведение к треугольному виду

Данный метод состоит в том, чтобы привести определитель к треугольному виду, а затем вычислить произведение элементов, стоящих на главной диагонали.

Пример 1

Вычислить определитель ∣4−20532−21−213−123−6−3∣begin{vmatrix}4&-2&0&5\3&2&-2&1\-2&1&3&-1\2&3&-6&-3end{vmatrix}.

Поменяем местами строки №1 и №3:

∣4−20532−21−213−123−6−3∣=−∣−213−132−214−20523−6−3∣begin{vmatrix}4&-2&0&5\3&2&-2&1\-2&1&3&-1\2&3&-6&-3end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\2&3&-6&-3end{vmatrix}.

Прибавим к строке №4 строку №1, умноженную на 1:

−∣−213−132−214−20523−6−3∣=−∣−213−132−214−20504−3−4∣-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\2&3&-6&-3end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\0&4&-3&-4end{vmatrix}.

Прибавим к строке №3 строку №1, умноженную на 2:

−∣−213−132−214−20504−3−4∣=−∣−213−132−21006304−3−4∣-begin{vmatrix}-2&1&3&-1\3&2&-2&1\4&-2&0&5\0&4&-3&-4end{vmatrix}=-begin{vmatrix}-2&1&3&-1\3&2&-2&1\0&0&6&3\0&4&-3&-4end{vmatrix}.

Умножим строку №2 на 2:

∣−213−132−21006304−3−4∣=−12∣−213−164−42006304−3−4∣begin{vmatrix}-2&1&3&-1\3&2&-2&1\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}begin{vmatrix}-2&1&3&-1\6&4&-4&2\0&0&6&3\0&4&-3&-4end{vmatrix}.

Прибавим к строке №2 строку №1, умноженную на 3:

−12∣−213−164−42006304−3−4∣=−12∣−213−1075−1006304−3−4∣-frac{1}{2}begin{vmatrix}-2&1&3&-1\6&4&-4&2\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&4&-3&-4end{vmatrix}.

Умножим строку №4 на 7:

−12∣−213−1075−1006304−3−4∣=−12⋅17∣−213−1075−10063028−21−28∣-frac{1}{2}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&4&-3&-4end{vmatrix}=-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&28&-21&-28end{vmatrix}.
Прибавим к строке №4 строку №2, умноженную на -4:

−12⋅17∣−213−1075−10063028−21−28∣=−12⋅17∣−213−1075−1006300−41−24∣-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&28&-21&-28end{vmatrix}=-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&0&-41&-24end{vmatrix}.

Поменяем местами столбцы №3 и №4:

−12⋅17∣−213−1075−1006300−41−24∣=12⋅17∣−21−1307−15003600−24−41∣-frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&3&-1\0&7&5&-1\0&0&6&3\0&0&-41&-24end{vmatrix}=frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&-24&-41end{vmatrix}.
Прибавим к строке №4 строку №3, умноженную на 8 и вычислим определитель:

12⋅17∣−21−1307−15003600−24−41∣=12⋅17∣−21−1307−1500360007∣=12⋅17⋅(−2)⋅7⋅3⋅7=−21frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&-24&-41end{vmatrix}=frac{1}{2}cdotfrac{1}{7}begin{vmatrix}-2&1&-1&3\0&7&-1&5\0&0&3&6\0&0&0&7end{vmatrix}=frac{1}{2}cdotfrac{1}{7}cdot(-2)cdot7cdot3cdot7=-21.

Пример 2

Вычислить определитель

∣7694−410−266789−1−61−1−245−70−92−2∣begin{vmatrix}7&6&9&4&-4\1&0&-2&6&6\7&8&9&-1&-6\1&-1&-2&4&5\-7&0&-9&2&-2end{vmatrix}.

Поменяем местами строки №1 и №4:

∣7694−410−266789−1−61−1−245−70−92−2∣=−∣1−1−24510−266789−1−67694−4−70−92−2∣begin{vmatrix}7&6&9&4&-4\1&0&-2&6&6\7&8&9&-1&-6\1&-1&-2&4&5\-7&0&-9&2&-2end{vmatrix}=-begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\7&8&9&-1&-6\7&6&9&4&-4\-7&0&-9&2&-2end{vmatrix}.

Поменяем местами строки №3 и №5:

−∣1−1−24510−266789−1−67694−4−70−92−2∣=∣1−1−24510−266−70−92−27694−4789−1−6∣-begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\7&8&9&-1&-6\7&6&9&4&-4\-7&0&-9&2&-2end{vmatrix}=begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\-7&0&-9&2&-2\7&6&9&4&-4\7&8&9&-1&-6end{vmatrix}.

Поменяем местами столбцы №4 и №5:

∣1−1−24510−266−70−92−27694−4789−1−6∣=−∣1−1−25410−266−70−9−22769−44789−6−1∣begin{vmatrix}1&-1&-2&4&5\1&0&-2&6&6\-7&0&-9&2&-2\7&6&9&4&-4\7&8&9&-1&-6end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\1&0&-2&6&6\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}.

Прибавим к строке №2 строку №1, умноженную на -1:

−∣1−1−25410−266−70−9−22769−44789−6−1∣=−∣1−1−25401012−70−9−22769−44789−6−1∣-begin{vmatrix}1&-1&-2&5&4\1&0&-2&6&6\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}.

Прибавим к строке №4 строку №3, умноженную на 1:

−∣1−1−25401012−70−9−22769−44789−6−1∣=−∣1−1−25401012−70−9−22060−66789−6−1∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\7&6&9&-4&4\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\7&8&9&-6&-1end{vmatrix}.

Прибавим к строке №5 строку №3, умноженную на 1:

−∣1−1−25401012−70−9−22060−66789−6−1∣=−∣1−1−25401012−70−9−22060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\7&8&9&-6&-1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.

Прибавим к строке №3 строку №1, умноженную на 7:

−∣1−1−25401012−70−9−22060−66080−81∣=−∣1−1−254010120−7−233330060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\-7&0&-9&-2&2\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&-7&-23&33&30\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.

Прибавим к строке №3 строку №2, умноженную на 7:

−∣1−1−254010120−7−233330060−66080−81∣=−∣1−1−2540101200−234044060−66080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&-7&-23&33&30\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}.

Вынесем из строки №4 множитель 6:

−∣1−1−2540101200−234044060−66080−81∣=−6∣1−1−2540101200−234044010−11080−81∣-begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&6&0&-6&6\0&8&0&-8&1end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&8&0&-8&1end{vmatrix}.

Прибавим к строке №5 строку №4, умноженную на -8:

−6∣1−1−2540101200−234044010−11080−81∣=−6∣1−1−2540101200−234044010−110000−7∣-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&8&0&-8&1end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&0&0&0&-7end{vmatrix}.

Прибавим к строке №4 строку №2, умноженную на -1 и вычислим определитель:

−6∣1−1−2540101200−234044010−110000−7∣=−6∣1−1−2540101200−234044000−2−10000−7∣=−6⋅1⋅1⋅(−23)⋅(−2)⋅(−7)=1932-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&1&0&-1&1\0&0&0&0&-7end{vmatrix}=-6begin{vmatrix}1&-1&-2&5&4\0&1&0&1&2\0&0&-23&40&44\0&0&0&-2&-1\0&0&0&0&-7end{vmatrix}=-6cdot1cdot1cdot(-23)cdot(-2)cdot(-7)=1932.

Мы рассмотрели наиболее распространенные методы вычисления определителей высших порядков. Каждый из них может применяться для их нахождения.

Онлайн-помощь с решением контрольных работ на бирже Студворк!

Тест по теме «Как вычислить определитель матрицы высших порядков»

Источник

Определители

Den_Che
Корумчанин
Преподаватель МИФИ

Поделиться этой страницей

Нулевой тип

Квадратный тип

Вектор-стобец

Вектор-строка

Диагональный тип

Единичная матрица

Канонический тип

Треугольный тип

Ступенчатая матрица

Приведение к треугольному виду

Задание 1

Задание 2

Приведение к ступенчатому виду

Разложение определителей по строкам или столбцам

Метод понижения порядка

Приведение к треугольному виду

Тест по теме «Как вычислить определитель матрицы высших порядков»

Не пропустите также: