Как найти окружность круга по формуле - AvtoShod.ru

8 способов найти длину окружности

Выбирайте формулу, ориентируясь на известные величины.

1. Как найти длину окружности через диаметр

Просто умножьте диаметр на число пи.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
d —диаметр окружности.

2. Как найти длину окружности через радиус

Умножьте число пи на два радиуса.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
r — радиус окружности.

3. Как вычислить длину окружности через площадь круга

Умножьте число пи на четыре площади круга.

Найдите корень из результата.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
π (пи) — константа, равная 3,14.

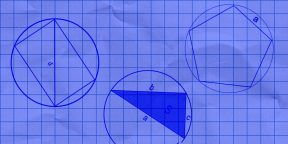
4. Как найти длину окружности через диагональ вписанного прямоугольника

Умножьте число пи на диагональ.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
d – любая диагональ прямоугольника.

5. Как вычислить длину окружности через сторону описанного квадрата

Умножьте число пи на сторону квадрата.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
a – любая сторона квадрата.

6. Как найти длину окружности через стороны и площадь вписанного треугольника

Перемножьте стороны треугольника.

Поделите результат на площадь и на два.

Умножьте полученное число на пи.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
S – площадь треугольника.
a, b, c – стороны треугольника.

7. Как найти длину окружности через площадь и полупериметр описанного треугольника

Поделите площадь треугольника на его полупериметр.

Умножьте результат на число пи и на два.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
S – площадь треугольника.
p – полупериметр треугольника (равен половине от суммы всех сторон).

8. Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разделите 180 градусов на количество сторон многоугольника.

Найдите синус полученного числа.

Разделите сторону многоугольника на результат.

Умножьте получившееся число на пи.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
π (пи) — константа, равная 3,14.
N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✏️🎓

Как найти периметр прямоугольника
8 способов найти периметр треугольника
7 способов найти площадь прямоугольника
Как перевести обычную дробь в десятичную
Как освоить устный счёт школьникам и взрослым

Источник

Как посчитать длину окружности

Главная
/
Математика
/
Геометрия
/
Как посчитать длину окружности

Чтобы посчитать длину окружности (круга) просто воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Для того чтобы определить длину окружности вам необходимо знать её радиус или диаметр, либо её площадь. Зная хотя бы один из этих параметров, введите его в соответствующие поле и получите результат в виде длины окружности (длины дуги в 360 градусов).

Как посчитать длину окружности зная диаметр

Какая длина у окружности если

её диаметр ?

Ответ:

Какова длина окружности (С) если её диаметр d?

Формула

С = π⋅d, где π ≈ 3.14

Пример

Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная радиус

Какая длина у окружности если

её радиус ?

Ответ:

Какова длина окружности (С) если её радиус r?

Формула

С = 2⋅π⋅r, где π ≈ 3.14

Пример

Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная её площадь

Какая длина у окружности если

её площадь ?

Ответ:

Какова длина окружности (С) если её площадь S?

Формула

С = 2π⋅√^S/_π, где π ≈ 3.14

Пример

Если площадь круга равна 6 см², то его длина примерно равна 8.68 см.

См. также

Источник

Загрузить PDF

Окружность – это плоская замкнутая кривая, все точки которой равноудалены от центральной точки.^[1] Длина окружности (С) – это длина замкнутой кривой, которая и образует окружность.^[2] Площадь круга (А) – это величина пространства, которое ограничено окружностью.^[3] Площадь круга и длина окружности вычисляются по формулам, в которых присутствует радиус (или диаметр) окружности и число «пи».

1
Формула для вычисления длины окружности. Длину окружности можно вычислить по двум формулам: C = 2πr или C = πd, где π – число «пи» (математическая константа, приблизительно равная 3,14)^[4], r – радиус окружности, d – диаметр окружности.^[5]
- Приведенные формулы по сути одинаковые, так как диаметр равен удвоенному радиусу.
- Длина окружности измеряется в любых единицах измерения длины: в метрах, сантиметрах, миллиметрах и так далее.
2
Величины формулы. В формулу для нахождения длины окружности входят три величины: радиус, диаметр и число «пи». Радиус и диаметр связаны друг с другом: радиус равен половине диаметра, а диаметр равен удвоенному радиусу.
- Радиус окружности (r) – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
- Диаметр окружности (d) – это отрезок, проходящий через центр окружности и соединяющий любые две точки, лежащие на окружности.^[6]
- Число «пи» (π) равно отношению длины окружности к ее диаметру; число «пи» представляет собой иррациональное число, которое примерно равно 3,14159265 и не имеет конечной цифры и повторяющихся сочетаний цифр.^[7] В большинстве математических вычислений число «пи» округляется до 3,14.
3
Измерьте радиус или диаметр окружности. Совместите начало линейки с любой точкой на окружности и сделайте так, чтобы линейка соприкасалась с центром окружности. Измерьте расстояние от точки до центра окружности, чтобы получить значение радиуса. Измерьте расстояние между двумя точками, лежащими на окружности, чтобы получить значение диаметра.
- В большинстве математических задач радиус или диаметр будет дан.
4
Подставьте значения величин в формулу. Найдя радиус и/или диаметр окружности, подставьте значение в соответствующую формулу. Если вы нашли радиус, воспользуйтесь формулой C = 2πr, а если диаметр, формулой C = πd.
- Пример: найдите длину окружности, радиус которой равен 3 см.
  - Напишите формулу: C = 2πr
  - Подставьте данное значение в формулу: C = 2π3
  - Перемножьте: C = (2*3*π) = 6π = 18,84 см
- Пример: найдите длину окружности, диаметр которой равен 9 м.
  - Напишите формулу: C = πd
  - Подставьте данное значение в формулу: C = 9π
  - Перемножьте: C = (9*π) = 28,26 м
5
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите длину окружности с диаметром 5 м.
  - C = πd = 5π = 15,7 м
- Найдите длину окружности с радиусом 10 м.
  - C = 2πr = C = 2π10 = 2*10* π = 62,8 м
Реклама

1
Формула для вычисления площади круга. Площадь круга можно вычислить по двум формулам, включающим диаметр или радиус: A = πr² или A = π(d/2)²^[8], где π – число «пи» (математическая константа, приблизительно равная 3,14)^[9], r – радиус круга, d – диаметр круга.
- Приведенные формулы по сути одинаковые, так как диаметр равен удвоенному радиусу.
- Площадь круга измеряется в любых единицах измерения длины, возведенных в квадрат: в квадратных метрах (м²), в квадратных сантиметрах (см²), в квадратных миллиметрах (мм²) и так далее.
2
Величины формулы. В формулу для нахождения площади круга входят три величины: радиус, диаметр и число «пи». Радиус и диаметр связаны друг с другом: радиус равен половине диаметра, а диаметр равен удвоенному радиусу.
- Радиус круга (r) – это отрезок, соединяющий центр круга с любой точкой, лежащей на окружности, которая ограничивает этот круг.
- Диаметр круга (d) – это отрезок, проходящий через центр круга и соединяющий любые две точки, лежащие на окружности, которая ограничивает этот круг.^[10]
- Число «пи» (π) равно отношению длины окружности к ее диаметру; число «пи» представляет собой иррациональное число, которое примерно равно 3,14159265 и не имеет конечной цифры и повторяющихся сочетаний цифр.^[11] В большинстве математических вычислений число «пи» округляется до 3,14.
3
Измерьте радиус или диаметр круга. Совместите начало линейки с любой точкой на окружности, ограничивающей круг, и сделайте так, чтобы линейка соприкасалась с центром круга. Измерьте расстояние от точки до центра круга, чтобы получить значение радиуса. Измерьте расстояние между двумя точками, лежащими на окружности, чтобы получить значение диаметра.
- В большинстве математических задач радиус или диаметр будет дан.
4
Подставьте значения величин в формулу. Найдя радиус и/или диаметр круга, подставьте значение в соответствующую формулу. Если вы нашли радиус, воспользуйтесь формулой A = πr², а если диаметр, формулой A = π(d/2)².
- Пример: найдите площадь круга с радиусом 3 м.
  - Напишите формулу: A = πr²
  - Подставьте данное значение: A = π3²
  - Возведите радиус в квадрат: r² = 3² = 9
  - Умножьте на число «пи»: A = 9π = 28,26 м²
- Пример: найдите площадь круга с диаметром 4 м.
  - Напишите формулу: A = π(d/2)²
  - Подставьте данное значение: A = π(4/2)²
  - Разделите диаметр на 2: d/2 = 4/2 = 2
  - Результат возведите в квадрат: 2² = 4
  - Умножьте на число «пи»: A = 4π = 12,56 м²
5
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите площадь круга с диаметром 7 м.
  - A = π(d/2)² = π(7/2)² = π(3,5)² = 12,25 * π= 38,47 м².
- Найти площадь круга с радиусом 3 м.
  - A = πr² = π3² = 9 * π = 28,26 м²
Реклама

1
Найдите радиус или диаметр окружности. В некоторых задачах радиус или диаметр дается в виде выражения с участием переменной, например, г = (х + 7) или d = (х + 3). В этом случае вы можете найти площадь круга или длину окружности, но окончательный ответ будет также содержать переменную. Запишите радиус или диаметр так, как дается в задаче.
- Пример: вычислите длину окружности с радиусом (х + 1).
2
Напишите формулу с данным значением. Вычисляя площадь круга или длину окружности, вы подставляете данное значение в соответствующую формулу. Сначала запишите формулу для вычисления площадь круга или длину окружности, а затем подставьте в нее значение диаметра или радиуса, выраженное переменной.
- Пример: вычислите длину окружности с радиусом (х + 1).
- Напишите формулу: C = 2πr
- Подставьте данное значение: C = 2π(х + 1)
3
Вычислите длину окружности так, как если бы переменная была представлена числом. На данный момент решите задачу, рассматривая переменную в качестве обычного числа. Возможно, вам придется использовать свойство дистрибутивности для упрощения окончательного ответа.
- Пример: вычислите длину окружности с радиусом (х + 1).
- C = 2πr = 2π (х + 1) = 2πx + 2π1 = 2πx + 2π = 6,28x + 6,28
- Если вы знаете значение переменной «х», подставьте его в найденное выражение, чтобы получить численный ответ.
4
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите площадь круга с радиусом 2х.
  - A = πr² = π(2x)² = π4x² = 12,56x²
- Найдите площадь круга с диаметром (х + 2).
  - A = π(d/2)² = π((x +2)/2)² = ((x +2)²/4)π
Реклама

Об этой статье

Эту страницу просматривали 212 798 раз.

Была ли эта статья полезной?

Источник

Окружность, круг, сегмент, сектор. Формулы и свойства

Окружность — определение
Круг — определение
Радиус и диаметр окружности
Основные свойства окружности
Формулы длины окружности и площади круга
Уравнение окружности
Касательная окружности и ее свойства
Секущая окружности и ее свойства
Хорда окружности и ее свойства
Центральный угол, вписанный угол и их свойства
Дуга, длина дуги, градусная мера дуги
Полуокружность и полукруг
Сектор, площадь сектора
Сегмент, площадь сегмента
Концентрические окружности
Кольцо

Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.

Определение. Единичная окружность — окружность, радиус которой равен единице.

Определение. Круг — часть плоскости, ограничена окружностью.

Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

1. Диаметр окружности равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Формулы длины окружности и площади круга

Формулы длины окружности

1. Формула длины окружности через диаметр:

L = πD

2. Формула длины окружности через радиус:

L = 2πr

Формулы площади круга

1. Формула площади круга через радиус:

S = πr²

2. Формула площади круга через диаметр:

S = πD²4

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:

r² = x² + y²

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r² = (x — a)² + (y — b)²

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

{	x = a + r cos t
y = b + r sin t

Касательная окружности и ее свойства

Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

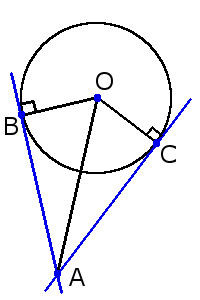
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Определение. Секущая окружности — прямая, которая проходит через две точки окружности.

Основные свойства секущих

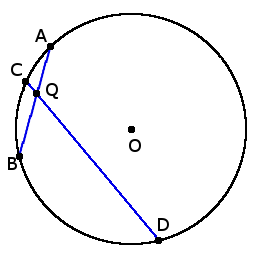
1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ²

Хорда окружности ее длина и свойства

Определение. Хорда окружности — отрезок, который соединяет две точки окружности.

Длина хорды

1. Длина хорды через центральный угол и радиус:

AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:

AB = 2r sin α

Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

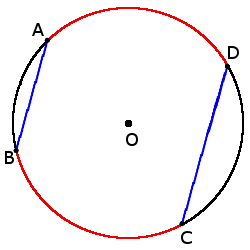
2. Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

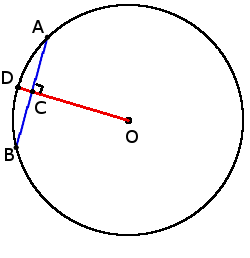
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

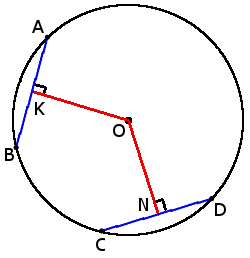
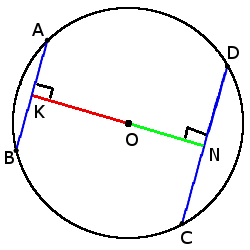
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

6. Чем больше хорда, тем ближе она к центру.

если CD > AB, то

ON < OK

Центральный угол, вписанный угол и их свойства

Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.

Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов

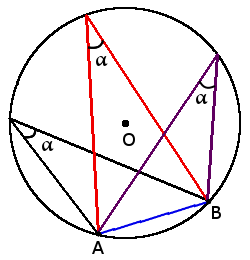
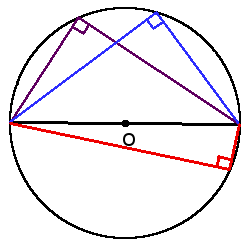
1. Все вписанные углы, которые опираются на одну дугу — равны.

2. Вписанный угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу

β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

α + β = 180°

Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.

Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.

Формула длины дуги через центральный угол (в градусах):

l = πr180°∙ α

Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.

Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.

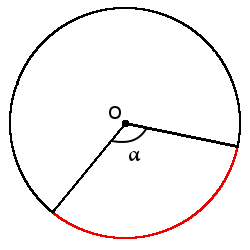
Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)

S = πr²360°∙ α

Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.

Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.

Источник

Формулы окружности

Окружность

Длины окружности и диаметр:

(С=pi*D)

Длина окружности:

(C = 2*pi*R)

Площадь круга:

(S=pi*r^2)

Площадь через диаметр:

(frac{pi*D}{4})

Уравнение окружности:

(r^2 = x^2 + y^2)

Выразим (R) из формулы (C = 2*pi*R) (—>) (R=frac{c}{2*pi}) подставим (R) в формулу (S=pi*r^2) (—>) (S=frac{C^2}{4*pi}). Получаем формулу площади через длину окружности и (pi):

(S=frac{C^2}{4*pi})

Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Источник

8 способов найти длину окружности

1. Как найти длину окружности через диаметр

2. Как найти длину окружности через радиус

3. Как вычислить длину окружности через площадь круга

4. Как найти длину окружности через диагональ вписанного прямоугольника

5. Как вычислить длину окружности через сторону описанного квадрата

6. Как найти длину окружности через стороны и площадь вписанного треугольника

7. Как найти длину окружности через площадь и полупериметр описанного треугольника

8. Как вычислить длину окружности через сторону вписанного правильного многоугольника

Как посчитать длину окружности

Онлайн калькулятор

Как посчитать длину окружности зная диаметр

Формула

Пример

Как посчитать длину окружности зная радиус

Формула

Пример

Как посчитать длину окружности зная её площадь

Формула

Пример

См. также

Об этой статье

Была ли эта статья полезной?

Окружность, круг, сегмент, сектор. Формулы и свойства

Основные свойства окружности

Формулы длины окружности и площади круга

Формулы длины окружности

Формулы площади круга

Уравнение окружности

Касательная окружности и ее свойства

Основные свойства касательных к окружности

Секущая окружности и ее свойства

Основные свойства секущих

Хорда окружности ее длина и свойства

Длина хорды

Основные свойства хорд

Центральный угол, вписанный угол и их свойства

Основные свойства углов

Не пропустите также: